斯格明子电子学的研究进展∗
赵巍胜 黄阳棋 张学莹 康旺 雷娜 张有光
(北京航空航天大学费尔北京研究院,大数据科学与脑机智能高精尖创新中心,电子信息工程学院,北京 100191)
在过去的半个世纪中,微电子技术一直沿着著名的摩尔定律快速发展,当前已经达到单芯片可集成上百亿晶体管.然而随着晶体管尺寸的缩小,因量子效应所产生的漏电流及其所导致的热效应使得这一定律遇到瓶颈.自旋电子技术由于引入了电子自旋这一全新的自由度,将有望大幅度降低器件功耗,突破热效应枷锁.斯格明子是一种具有拓扑保护的类粒子自旋结构,有望成为下一代自旋电子信息载体,引起了从物理到电子领域的广泛关注.由于其特殊的拓扑性质,斯格明子具备尺寸小、结构稳定、驱动阈值电流小等诸多优点,室温下斯格明子的成核、输运及探测进一步验证了其广泛的应用潜力,由此诞生了研究相关器件及应用的斯格明子电子学.本综述从电子学角度首先介绍斯格明子的基础概念及发展现状、理论及实验研究方法,重点阐述斯格明子器件的写入、调控及读取功能,介绍了一系列具有代表性的新型信息器件;最后,结合斯格明子电子学现状分析了目前所面临的发展瓶颈以及未来的应用前景.
1 引 言
1965年,英特尔公司联合创始人戈登·摩尔(Gordon E.Moore)预测基于微电子技术的集成电路晶体管数量及其所对应的运算性能将每18个月翻一倍,这就是著名的摩尔定律(Moore’s law)[1].在过去50年中,这一定律描绘了从第一台家用电脑到当今随处可见的精密计算机、智能手机,以及各式各样智能硬件的迅猛发展.然而随着单芯片晶体管密度越来越大,器件的功耗与散热也变得超出了可承受的范围,摩尔定律即将失效[2].芯片的工作频率无法进一步提高,依靠多核集成的方法可以降低静态功耗,但影响了工作性能.另一方面,分离的存储介质与处理芯片之间的数据传输消耗了超过芯片一半的功耗.如何进一步降低计算系统功耗、突破芯片散热瓶颈已经成为当前电子领域所面临的核心问题.
1988年,法国科学家艾伯特·费尔(Albtert Fert)和德国科学家彼得·格林贝格(Peter Andreas Grünberg)共同发现了巨磁阻效应(giant magnetoresistance,GMR)[3],该效应很快被应用于计算机的硬盘磁头,使其容量在1997年之后的十年间增长了1000倍,引发了数据存储领域的产业革命,并开创了一门新兴的学科——自旋电子学(Spintronics)[4].自旋电子器件具有静态功耗低、可无限次高速读写、非易失性存储等优点,被认为是突破当前瓶颈的关键技术,受到了广泛关注.随后,自旋电子学迅速地发展起来,并获得了一系列重要研究成果.例如,隧穿磁电阻效应(tunnel magnetoresistance,TMR)[5−8]、自旋转移矩(spin transfer torque,STT)[9,10],自旋轨道矩(spin orbit torque,SOT)等[11−14]效应的发现,使得实用的自旋电子器件成为可能.2006年,基于自旋电子技术的磁阻式随机存储器(magnetic random access memory,MRAM)开始商用,在航空航天等高可靠性领域发挥着重要作用[15].自2018年底,三星(Sam sung),台积电(TSMC)、格罗方德(G lobal-Foundries)、联华电子(UMC)等全球领先半导体企业都计划量产STT-MRAM,这将推动自旋电子技术进一步的快速发展.近年来,磁结构中的拓扑属性及其相关应用被认为将可能成为下一代自旋电子器件的信息载体,是目前该领域的研究热点之一.
2 斯格明子的概念定义及发现过程
斯格明子(skyrmion)一词源自英国核物理学家托尼·斯格明(Tony Skyrme).他在60年代提出了一套用于描述介子(pion)间相互作用的非线性场理论,并进一步预言了一种具有拓扑保护性质的类粒子稳定场结构的存在,即斯格明子[16].这一结构在液晶[17],玻色-爱因斯坦凝聚[18],量子霍尔磁体等[19]不同领域中均有发现.1975年,Belavin和Polyakov[20]在理论上提出了一种存在于二维铁磁体中的类粒子亚稳态,即本文所研究的磁性斯格明子(下文中均简称为“斯格明子”).它是一种在拓扑结构上非平庸的具有涡旋组态的手性自旋结构[21].相较于平庸的磁性结构,斯格明子在能量上具有拓扑不连续性,因而具有更高的稳定性.20世纪90年代,理论物理学家们又成功地预言了二维电子气的量子霍尔态中存在斯格明子[19,22].但是一直到2006年,Rößler等[23]才第一次在理论上证实了自发稳定存在的斯格明子态广泛地存在于具备空间反衍对称性破缺的磁性薄膜或体材料中.其中,体材料主要指具有B20晶格结构的磁体,如FeGe,MnSi等.2009年,在磁性材料体系中第一次在实验上观测到斯格明子,即是在MnSi手性材料中[24−26].紧接着,Heinze团队[27]于2011年在Fe/Ir磁性薄膜体系中观测到了二维斯格明子阵列.在此之后,多种不同体系中斯格明子的拓扑自旋结构得到了广泛的研究[28−30].2013年,Fert团队[31,32]通过微磁学模拟建模的方法,系统研究了单个斯格明子在多层膜纳米带结构中的产生、稳定性以及电流驱动现象,提出斯格明子可以作为新一代自旋电子器件中的信息存储载体.之后,多个课题组在不同的材料和结构体系下发现了室温[33−38]、甚至高于室温条件下[39,40]稳定存在的斯格明子,进一步从实验上证实了斯格明子相关器件的可行性;一些全新的材料体系中的斯格明子也不断被发现[28,41,42].近年来,随着对斯格明子的深入研究,从存储[31]、逻辑[43,44]到新一代非冯·诺依曼体系计算架构[45−47]的相关的器件及应用场景被提出,由此产生了一门新型交叉分支学科——斯格明子电子学[48−50].
3 斯格明子的拓扑稳定性及Dzyaloshinskii-Moriya相互作用
在磁性材料中,斯格明子的产生源自多种物理机理及其之间的协同作用.其中主要包括以下四种机理:1)长程磁偶极相互作用(long-ranged magnetic dipolar interactions),在具有垂直磁各向异性的磁性薄膜中,该相互作用与磁各向异性形成竞争,从而产生周期性的磁条带,并在垂直方向外磁场的作用下,转化为斯格明子阵列,由此所产生的斯格明子尺寸一般较大,直径在100 nm—1µm之间[51−53];2)Dzyaloshinskii-Moriya相互作用(DM相互作用)[54,55],源自磁体晶格或磁性薄膜界面处的对称性缺失.由于交换相互作用倾向于使相邻磁矩呈现平行或反平行排列,而DM相互作用倾向于使相邻磁矩垂直排列,从而降低了斯格明子在铁磁态背景中所具有的能量,使得其能够稳定存在,该类型的斯格明子尺寸取决于DM相互作用的大小,通常在5—100 nm之间;3)阻挫交换相互作用(frustrated exchange interactions)[56];4)四自旋交换相互作用(four-spin exchange interactions)[27].其中3)和4)情况下的斯格明子尺寸与材料晶格尺寸相当,约1 nm.由于在1)和2)情况下,斯格明子及斯格明子阵列尺寸大于晶格常数,满足连续性近似条件,且相应的斯格明子能量密度远小于原子间的交换能J,使得该型斯格明子能够被相对容易地产生及消灭,并同时具有容易移动、不受晶格钉扎影响的特点.由于DM相互作用所产生的斯格明子相对磁偶极相互作用下的斯格明子尺寸更小,是斯格明子电子器件的理想信息载体,因而本文着眼于研究该类型斯格明子.
相邻两原子自旋之间DM相互作用对应的哈密顿量可以用如下公式表示:
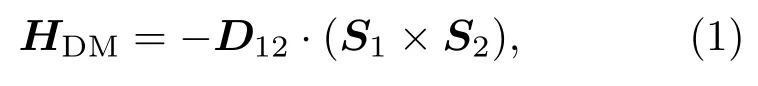
其中D12是DM矢量,S1和S2是相邻两原子间的原子自旋.这一效应产生于一种三端的间接交换机理,即相邻两原子自旋与另一相邻的具有强自旋轨道耦合的原子相互耦合[57,58].由于DM矢量的方向不同,可以形成两种不同的斯格明子,即奈尔型(Néel type)与布洛赫型(Bloch type),如图1所示.其自旋周期长度均正比于交换相互作用系数J与DM相互作用系数D的比值J/D,在数纳米到数微米之间[59].体材料中的斯格明子大多都属于布洛赫型,而薄膜材料中由于DM矢量平行于薄膜平面,则会形成奈尔类型斯格明子.
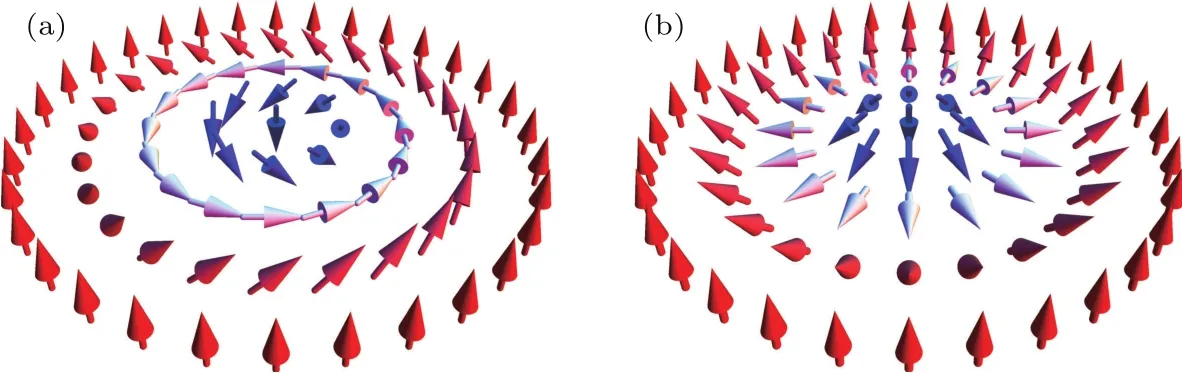
图1 (a)布洛赫型斯格明子,其横截面为布洛赫型的手性磁畴壁;(b)奈尔型斯格明子,其横截面为奈尔型的手性磁畴壁Fig.1.(a)B loch-skyrmions with cross section as bloch type chiral domain walls;(b)Néelskyrmions with cross section as Néel type chiral domain walls.
斯格明子的拓扑属性可以用斯格明子数(skyrmion number)进行描述,其定义如下:
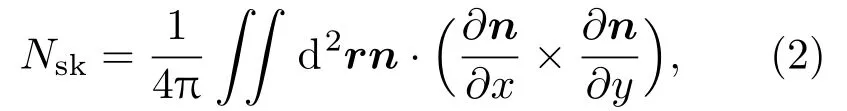
其中n为自旋单位方向矢量.该式描述了自旋在拓扑单位圆上环绕的圈数[60].斯格明子所对应的斯格明子数恰好为±1,同时也存在其他整数的情况,例如斯格明子数为2的双斯格明子.斯格明子数为整数的磁性结构不能连续变化为斯格明子数为0的铁磁态或是其他结构,因而具有拓扑稳定的特性[31].由于其拓扑结构的特殊性质,斯格明子相关的许多独特的拓扑现象已经引发了新一轮的研究热潮.例如具有DM相互作用磁体中的斯格明子及其霍尔输运[61,62]、热流与斯格明子的相互作用[63],电流驱动下斯格明子的相关运动及其控制等[64].
近年来,由斯格明子衍生出的一系列全新的拓扑相关自旋结构也引起了广泛的关注.南京大学丁海峰团队[65,66]预测了在无DM相互作用的磁性体系中利用层间耦合产生了人工斯格明子(artificial skyrmion),其优点是能够在较大的温度范围内保持结构的稳定,该结构在之后被多个美国研究团队实验验证.中国科学院物理研究所王文洪团队[67]在M nNiGa中发现了双斯格明子(biskyrmion),这一特殊结构在具有宽域温度稳定性(100—340 K)的同时,可以更加容易地实现输运.中科院强磁场科学中心的杜海峰团队及其合作者在强边界约束的手性磁纳米盘中观测到了靶斯格明子(target skyrmion),可以在无外场的情况下稳定存在[68].此外,Nagaosa团队[69]利用仿真验证了具有相反斯格明子数的拓扑涡旋结构反斯格明子(antiskyrmion).该结构在手性磁体中无法稳定,但是可以在偶极磁体中存在.其斯格明子数反号,具备许多新的拓扑性质.另一种新的结构——多环斯格明子(skyrmionium)具有斯格明子数为零的特点[70−72].由于其特殊的拓扑性质,该结构在自旋流作用下不会发生斯格明子霍尔效应,同时具有更高的移动速率,在动力学特性方面具有独特的优势.
4 斯格明子的主要研究方法
4.1 微磁仿真计算
为了研究斯格明子及其特殊的拓扑自旋结构在产生、电流驱动等方面的性质,Fert等[31,32]在2013年建立了首个斯格明子微磁学模型.他们在传统的微磁学模拟中加入了DM相互作用所对应的哈密顿量,如(1)式所示.
在一个连续的磁化模型之中,(1)式可以进一步推导为
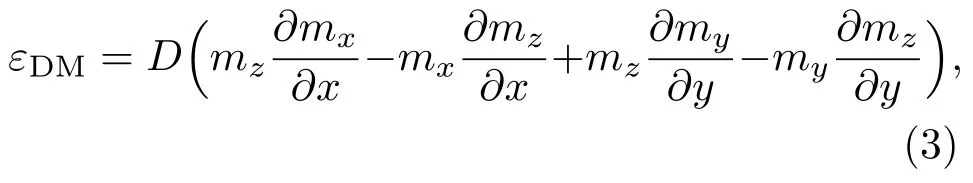
其中εDM表示DM相互作用所对应的能量密度;mx,my,mz分别代表x,y,z方向的归一化磁化强度,即m=M/Ms,Ms为样品的饱和磁化强度,在均匀系统中可以作为常数处理.(3)式中的D是一个与DM矢量相关的数值,其大小可以用(4)式计算,
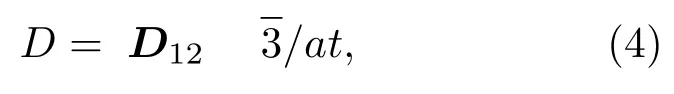
其中j D12j表示DM矢量D12的模长;a为铁磁原子的原子晶格常数,通常在1 nm左右;t则表示铁磁层的薄膜厚度.
将DM相互作用代入传统的微磁学模型,求解Landau-Lifshitz-Gilbert方程(LLG方程),从而获得铁磁材料中具体的磁化分布.其方程形式如下[73−75]:
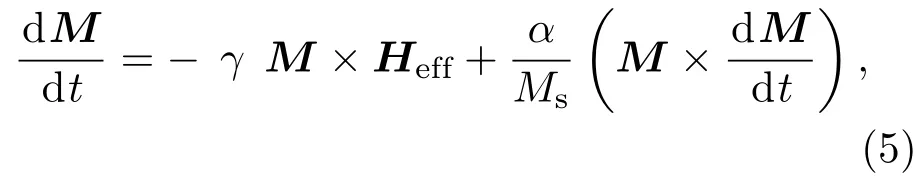
其中M为磁化强度,Heff是等效磁场,γ是吉尔伯特旋磁比,α则是阻尼系数.该等效磁场又可以用(6)式表示,
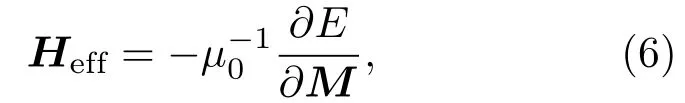
µ0是真空磁导率,而E是与磁化强度相关的平均能量密度.该能量密度包括4种不同的贡献来源,分别为交换能(exchange energy),磁各向异性能(anisotropy energy),塞曼能(zeem an energy),退磁能(demagnetic energy)以及新加入的DM相互作用能.因此,总能量密度E可以用(7)式表达:
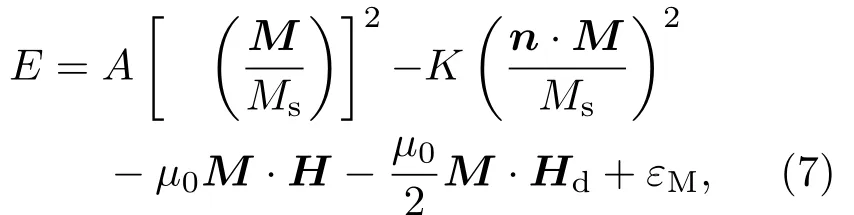
式中,A,K分别表示交换能和磁各向异性能常数;H与Hd分别表示外加磁场及退磁场.
通过以上方程的求解,可以清楚地了解到铁磁材料中磁矩随着时间的变化情况.为了进一步研究斯格明子在电流驱动下的行为,还需加入由电流所导致的扭矩项.根据电流自旋注入方式的不同,可以把其分为面内注入型与垂直注入型.
面内注入的电流磁矩主要来自铁磁层中电流所导致的STT.该磁矩包括绝热项(adiabatic torque)与非绝热项(non-adiabatic torque),表示如下:
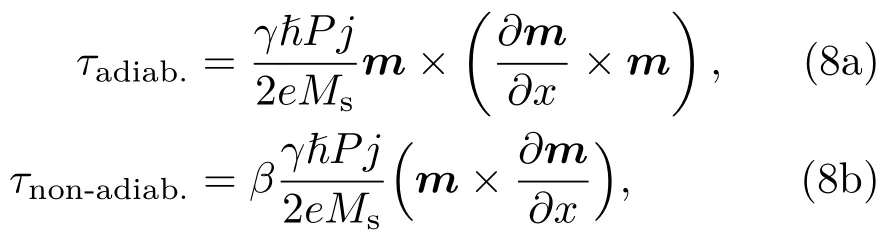
式中,γ为旋磁比,}为约化普朗克常量,P为自旋极化系数,j为电流密度,β为非绝热因子[76].
而对于垂直注入的自旋极化电流来说,其所导致的自旋矩主要包括两项,即面内项(in-plane torque)以及垂直平面项(out-of-plane torque).表达如下[77]:
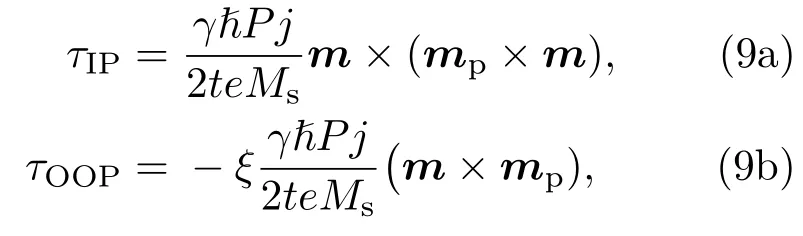
式中,t为磁性薄膜厚度,ξ为一个与面内磁矩大小相关的垂直磁矩幅度系数,mp为电流的自旋极化矢量.这一自旋注入方式通常可以通过自旋霍尔效应获得.
4.2 实验观测方法
2009年,Mühlbauer等[24]首次在实验上使用中子散射的方法观测到了斯格明子.利用这一方法,他们在具有B20晶体结构的MnSi块材中成功观测到斯格明子在倒空间中所形成的中子衍射点,并给出了该体系下斯格明子存在的条件相图,如图2所示.
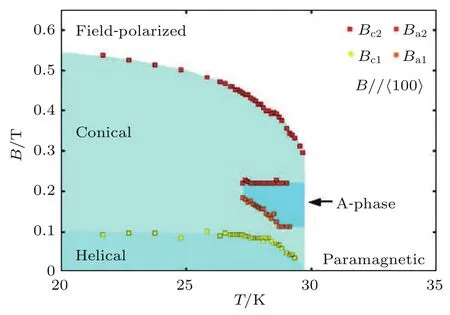
图2 MnSi的磁性相图,图中A-phase即对应斯格明子相态[24]Fig.2.Phase map of magnetization in MnSi.The A-phase is corresponding to the skyrmion state[24].
但是,中子散射仅仅能探测到斯格明子的存在,并不能给出其实空间的磁矩分布.2010年,Nagaosa团队利用洛伦兹透射电子显微镜(Lorentz transmission electron microscopy,LTEM)解决了这一问题[28],并在之后被广泛地应用于MnSi等[78,79],FeGe[68,80−82]B20结构样品中斯格明子的观测.具体的测试方法是分别利用LTEM在正焦(in-focus)、欠焦(under-focus)、以及过焦(overfocus)状态下对Fe0.5Co0.5Si薄膜样品的同一区域进行成像,如图3(a)—(c)所示.将这三种测试结果进行磁强度传输方程的计算(magnetic transport of-intensity equation calculation,TIE计算),即可得出面内的磁结构分布信息.强度传输方程表示为
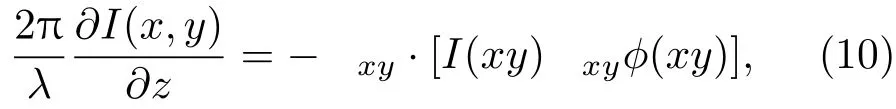
式中,I(x,y)和ϕ(xy)分别表示电子波的强度分布与相位分布.λ为电子波的波长.而根据麦克斯韦-安培方程(Maxwell-Ampere equation),电子波相位分布ϕ(xy)与磁化强度m具有如下关系:
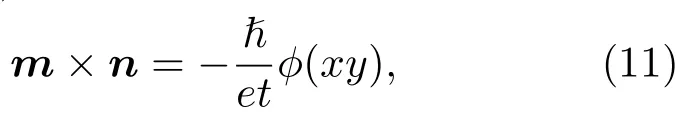
n为平行于电子束方向的单位矢量,t为样品厚度.

图3 (a)欠焦、 (b)过焦、 以及(c)正焦状态下Fe0.5 Co0.5Si薄膜的LTEM 图像;(d)经过强度传输方程计算后得到样品的面内磁场分布[28]Fig.3.(a)Under-focused,(b)over-focused,(c)infocused LTEM image of Fe0.5Co0.5Si thin films;(d)In plane magnetization distribution of the sample acquired by TIE calculation.
另一种具有足够分辨率、能够在实空间观测到斯格明子的方法是利用X射线穿透样品.2016年,Fert团队[33]及Beach团队[34]分别利用扫描X射线透射显微镜(scanning X-ray transmission microscopy,STXM)发现了室温下(Ir/Co/Pt)10多层膜和Pt/Co/Ta结构中稳定存在的斯格明子.同年,Boulle等[83]也通过X射线磁圆二色光电子显微镜(photoemission electron microscopy combined with X-ray magnetic circular dichroism,XMCDPEEM)观测到了室温下Pt/Co/MgO结构中的斯格明子.
虽然利用X射线可以取得足够精确的分辨率,但是实验条件苛刻,实验过程复杂.近年来,磁力显微镜(magnetic force microscopy,MFM)也被广泛地应用于观测材料表面纳米尺度的斯格明子结构[84],甚至可以动态地表征其运动[85].而对于尺寸较大的斯格明子(微米级)来说,极性磁光克尔显微镜(polar magneto-optical Kerr effect(MOKE)microscope)能够更加方便、直观地观测到斯格明子.实际上第一个在室温下观测到的斯格明子即是采用这种相对简单易行的方法[36].
5 斯格明子电子学基础
5.1 斯格明子的成核
斯格明子是具有拓扑保护的自旋结构,因此,在斯格明子成核的过程中需要克服其拓扑稳定性势垒[32].实际操作中,可以通过多种途径实现这一目标,包括外加磁场、局域热效应、自旋波、电流等方式.外加磁场可以改变系统的整体能量,从而获得斯格明子稳定存在的能量相态.如前文所述,当外加磁场与系统温度处于某一区间(A-phase)时,在B20结构材料体系(MnSi,FeGe等)中的自旋分布会出现由斯格明子组成的能量基态[86−89],并产生整齐排列的斯格明子阵列(skyrmion lattice).最早观察到的斯格明子即是采用这种方式在MnSi块材中激发得到[24].通过将MnSi材料做成具有菱形截面的纳米线,甚至可以通过外加磁场精确控制在其截面产生及湮没的斯格明子[90].进一步通过对FeGe的研究发现,这一方法得到的斯格明子会首先在材料的缺陷[91]或是边缘[92,93]处成核.另一种方法则是利用激光在磁性材料局域产生焦耳热,从而克服系统能量壁垒产生斯格明子.Nagaosa团队[94]与Finazzi团队[95]分别就理论及实验角度证实了这一构想.类似的方法还有使用自旋波的叠加,也同样可以赋予铁磁材料的局部以较高的能量,从而实现斯格明子的产生及湮没[96].以上方法虽然能够有效地使得斯格明子成核,但是由于需要使用磁场、激光等外部手段,并不适用于斯格明子器件的应用.因此,电学方法产生斯格明子具有更加实际的应用价值,受到广泛的关注.
数学模拟证明在具有DM相互作用的磁性纳米盘中垂直通过的自旋极化电流将能够产生斯格明子或是类似的具有拓扑属性的磁性涡旋结构[97−99].更一般的情况下,在平面的磁性材料结构中利用一束极细的自旋极化电流注入处于铁磁态的样品中,翻转局部的磁矩方向,在合适的DM相互作用下,系统将最后稳定为一个单独的斯格明子,如图4(a)所示[32,50].然而这一方法所需要的电流密度相对较大(一般为1012A/m2量级),通过磁性隧道结(magnetic tunneling junction,MTJ)无法实现这一构想.因此,在设计中我们提出采取自旋阀(spin valve)进行垂直自旋注入的设计[100].我们发现,具有微波振荡的驱动电流相较于直流驱动电流能够更加有效地产生斯格明子,并显著地降低阈值电流密度.当驱动电流振荡频率接近畴壁回转模式频率时,激发斯格明子所需的电流密度最小(约1.4×1012A/m2,同一模型无微波辅助情况下,阈值电流密度约1.8×1012A/m2)[101].同时,在特定情况下,这一结构还能产生具有更高斯格明子数(例如斯格明子数为2)的拓扑结构[102],是研究类似结构的常用自旋注入方法.
在实验上,W iesendanger团队[103]利用自旋极化的扫描隧穿显微镜(spin polarized scanning tunneling microscopy,SP-STM)实现了局部磁矩的翻转.他将自旋极化电流通过SP-STM的探针注入到Ir基底的FePd双层膜上,实现了对单个斯格明子产生及湮没的精确控制,如图4(b)所示.进一步地,将自旋极化的探针替换为非磁性探针,自旋极化的电流替换为电场,也观测到了类似的斯格明子产生及湮没[104].
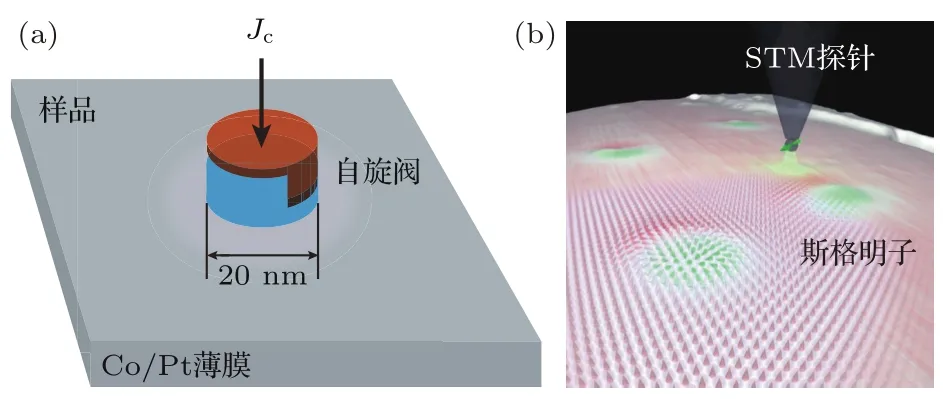
图4 (a)利用垂直注入的自旋极化电流产生斯格明子的器件构想;(b)通过SP-STM的探针在材料局部注入自旋极化电流,从而翻转局部磁矩,产生斯格明子[103]Fig.4.(a)The structure of skyrmion nucleation device with out-of-plane spin polarized current injection;(b)local in jection of spin polarized current by STM tip.A skyrmion is nucleated by switching the local magnetization[103].
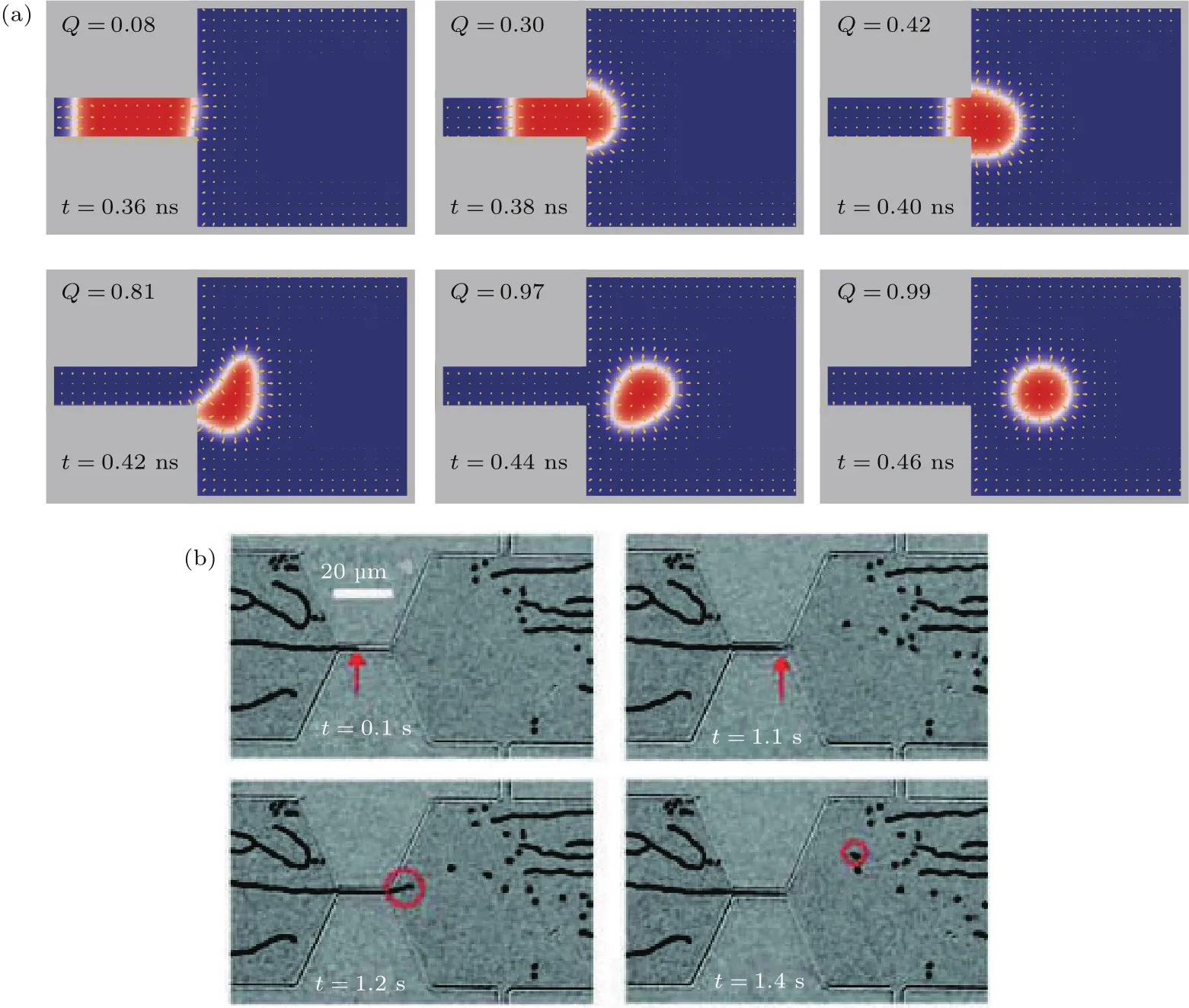
图5 (a)斯格明子可以通过一对窄带中的DW推动到宽带中获得[105];(b)在实验上通过类似结构产生微米级别的斯格明子已经得到证实[36]Fig.5.(a)Skyrm ions can be nucleated by driving DW from narrow tracks into wide tracks[105];(b)this theoretical prediction is already demonstrated by experiment[36].
另一种方法是利用磁畴壁(dom ain wall,DW)在特定结构中转化为斯格明子.这一方法最初由周艳团队通过仿真进行证实[105].在这一设计中,一段较窄的纳米线(窄线)和一段较宽的纳米线(宽线)相连接.在电流的作用下,一对包含数据信息的DW被从窄线推到宽线中.由于不同位置的DW在此过程中会受到不同方向的自旋矩,最终将导致一种具备拓扑保护性质的斯格明子磁泡的产生,如图5(a)所示.2015年,Hoffmann团队[36]首次在实验中利用类似器件结构实现了微米尺度斯格明子与DW的转换,如图5(b)所示,从实验上证实了这一方法的可行性.这也是实验中首次在室温下直接观测到的斯格明子产生,为斯格明子的相关应用奠定了基础.相关实验结果及其理论分析[106,107]也进一步揭示了非均匀的自旋极化电流产生斯格明子的作用机理.最新的研究表明,更小的纳米尺寸的斯格明子同样可以通过在纳米线中通入自旋电流得到[85].
5.2 斯格明子的输运
当一个电子在连续变化的非共线磁体中运动时,其自旋取向随磁矩方向而时刻变化,并且在电子与磁结构间产生一个相互作用力[108−112].斯格明子由于其特殊的拓扑自旋结构,当载流子经过斯格明子时会对其产生一个驱动力[113−115],同时斯格明子的运动又会产生一个继承其拓扑属性的新型磁场[116].相对DW而言,斯格明子在电流驱动下具有更高的耦合效率,因而将有望大幅降低操控电流密度[117],实现高效低功耗的信息传输[31].在纳米线中,斯格明子可以被两种电流导致的效应驱动,即铁磁层中的面内电流产生的STT,以及由重金属层中电流的自旋霍尔效应(spin hall effect,SHE)所产生的SOT,如图6所示[32,49,50].
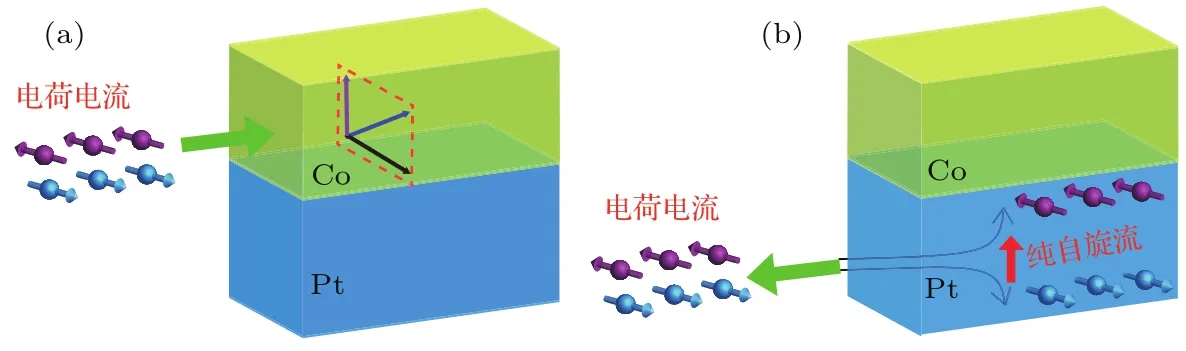
图6 (a)STT和(b)SOT驱动斯格明子时电流的作用方式示意图Fig.6.Schematic diagrams of(a)STT and(b)SOT driven skyrmions.
这两种转矩所对应的具体形式已在前文关于仿真方法的讨论中详细说明.在上述自旋矩作用下的斯格明子运动可以用蒂勒方程(Thiele equation)[118−120]进行描述.在不加入电流所引发的自旋矩的情况下,该方程可表示为[32]
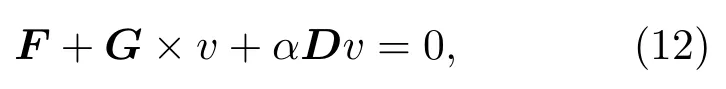
其中v是斯格明子的运动速度;F代表施加于斯格明子的外力,在纳米线等受限运动结构中一般来自于边界;G是陀螺向量;α为阻尼系数;D为耗散矩阵.假设斯格明子在运动过程中形状并未发生改变,纳米线的长度方向为x方向,垂直薄膜方向为z方向,则陀螺向量G可以写为G=(0,0,4πQ),Q为斯格明子所对应的斯格明子数(skyrmion number).此时,耗散矩阵D则可以写为
在STT作用的情况下,(12)式可表达为
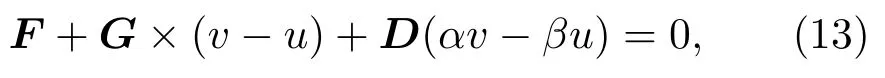
其中β为STT项中的非绝热因子;u为导电电子的迁移速度,为电流的自旋极化率;a为铁磁材料的晶格常数;Ms为饱和磁化强度;j为电流密度.
由(13)式可以导出斯格明子在纳米线中的运动速度如(14)式所示:

同时,斯格明子还会受到y方向的马格努斯力[121],并在y方向产生一个偏移[31,64,122].由于受到纳米线边界的排斥作用[123],随着斯格明子在y方向坐标的变化,其所受到的力F可以近似地表示为F=−kyey,ey为y方向单位向量.当斯格明子沿x方向稳定运动时,将在y方向出现一个恒定的偏移量.将F代入(13)式,可以得出此偏移量的表达式为
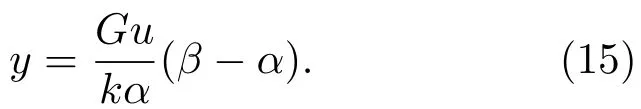
从上述公式可以看出,α与β的比值直接决定了斯格明子的运动速度与偏移量.当α=β时,斯格明子的运动速度与载流子运动速度一致(v=u);且这时斯格明子在y方向上的偏移量为0.当斯格明子在随空间变化的α与β中运动时,可以明显地观察到其运动轨迹随着参数的变化而变化[124].
对于SHE所产生的SOT作用下的斯格明子运动,可以将(12)式改写为如下形式[125]:
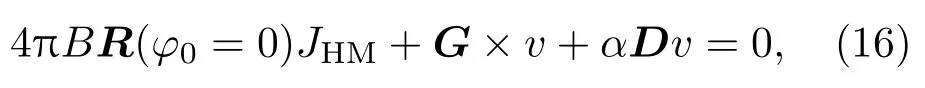
其中B与SHE相关;R为面内的旋转矩阵;JHM为重金属层中的电流密度,也即产生自旋霍尔效应的电流.求解(16)式可以得到在这一情况下斯格明子在x与y方向均获得一速度:
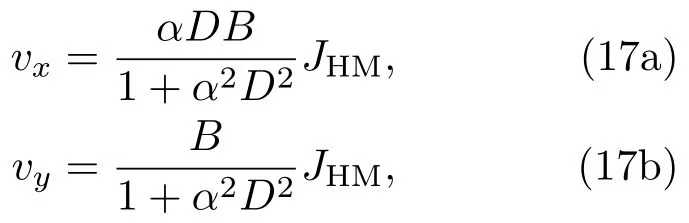
由(17)式可以得出此时斯格明子在x与y方向同时获得一与自旋霍尔电流成正比的速度,其运动轨迹将沿x方向呈现一夹角.在y方向运动受到限制的纳米线中,斯格明子受到边界的作用,将沿x方向稳定运动,并在y方向具有一定偏移,如图7(a)所示.
斯格明子在不同方式的驱动电流作用下具有不同的速度表达式,通过仿真计算可以得到在同一体系下斯格明子的速度随电流密度的变化规律,如图7(b)所示.随着驱动电流密度的增加,斯格明子的速度呈线性增长,符合公式中的正比关系.对比STT与SOT两种驱动模式,可以看出在相同驱动电流密度的情况下,SOT可以获得更高的效率[125].同时,由于SOT产生于电阻率更低的重金属层中,使得其在相同电流密度下功耗更低.因此,在斯格明子赛道存储器设计中,以SOT作为驱动源能够获得更快的器件速度与更好的能效性能.
斯格明子的电流驱动相对于以往运用于赛道存储器的磁畴壁来说具有相似的速度表达式和电流密度与速度的比例关系.但是,由于斯格明子特殊的拓扑属性,使得其具备明显的优点:更低的阈值驱动电流以及对于器件中缺陷的鲁棒性[31,32,64,122].通常情况下,要驱动DW运动的阈值电流在1011—1012A/m2,而驱动斯格明子理论上只需要106A/m2的电流,比DW低5到6个数量级.这也代表着斯格明子可以更加精确地被电流控制.理论研究同时证明了斯格明子在样品存在缺陷的情况下可以灵活地绕开缺陷,从而避免了DW赛道中由缺陷导致的DW钉扎等问题.相关实验工作也进一步展示了电流驱动下的斯格明子动力学特性.首先,斯格明子可以在纳米线中被电流驱动,但遗憾的是在驱动效率上目前理论和实验并不能很好地符合,驱动斯格明子所需的阈值电流较理论值偏高(108—1011A/m2).这是由于纳米线结构与材料中的缺陷间隔往往小于斯格明子尺寸,使其不能如理论一样绕过缺陷[34,36].其次,斯格明子霍尔效应,即在y方向存在的偏移,也在实验上被直接观测到[126,127].
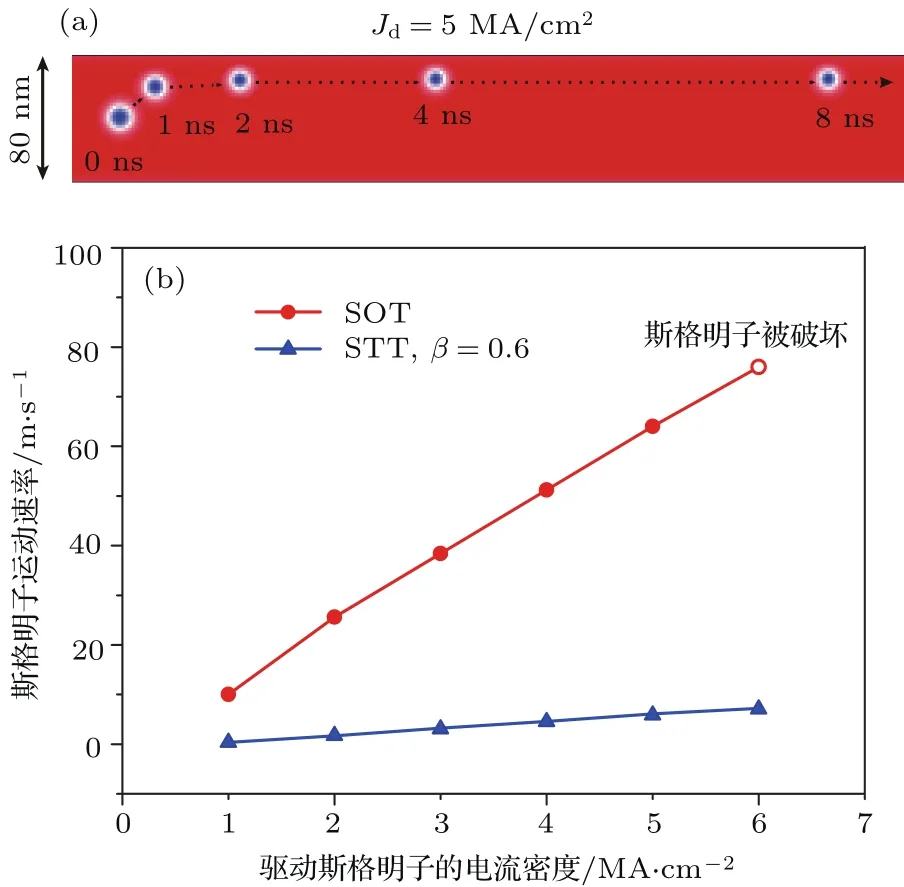
图7 (a)斯格明子在SOT作用下运动会发生一个垂直于纳米线方向的偏移;(b)受限纳米线结构中斯格明子在STT与SOT作用下运动速率与电流密度的关系,当SOT电流过大时,斯格明子偏移过大,会受到边界作用被破坏Fig.7.(a)A transverse motion of skyrmions will occur with SOT driven current;(b)in constricted geometry,the relation between skyrmion moving speed and current density driven by STT and SOT,respectively.With a large SOT driven current,skyrmions will be driven too close to the edge of the track and annihilated.
在斯格明子器件的相关研究中,斯格明子霍尔效应会导致斯格明子沿y方向偏移.由于纳米线边界会对斯格明子运动产生一定的阻尼效应[128],斯格明子沿y方向运动距离越大,其x方向速度越低.当电流足够大时,过大的y向马格努斯力甚至会破坏斯格明子,使其湮没[123].为避免斯格明子湮没造成的信息丢失,一种方法是优化纳米线边界条件,使得斯格明子在边界具有更高的势能,从而提高斯格明子受到的边界排斥力[129,130].另一种方法则可以通过控制斯格明子驱动电流来实现.由于在器件中,通常需要逐个写入和读取斯格明子序列中的信息,驱动斯格明子的电流往往并非连续电流.在仿真中,斯格明子在驱动电流关闭后会继续受到边界排斥力,从而回到纳米线y方向的中心位置.在原本会导致斯格明子湮没的电流密度下,通过控制驱动电流的脉冲持续时间和间隔时间,可以避免斯格明子被移出纳米线[100],如图8(a)所示.这样的设计既利用较大的驱动电流增大了斯格明子迁移速率,同时也保证了斯格明子的完整性.这一研究同时表明,为了使斯格明子不至于湮没在纳米线边界而能取得的最大电流密度与纳米线的宽度密切相关,宽度越大,斯格明子可承受的驱动电流也越大,同时代表着其迁移速率的增加,如图8(b)所示.由此可见,器件的运行速率(斯格明子迁移速率)与器件面积(纳米线宽度)存在竞争关系,在器件设计中需要对速率与密度进行取舍.
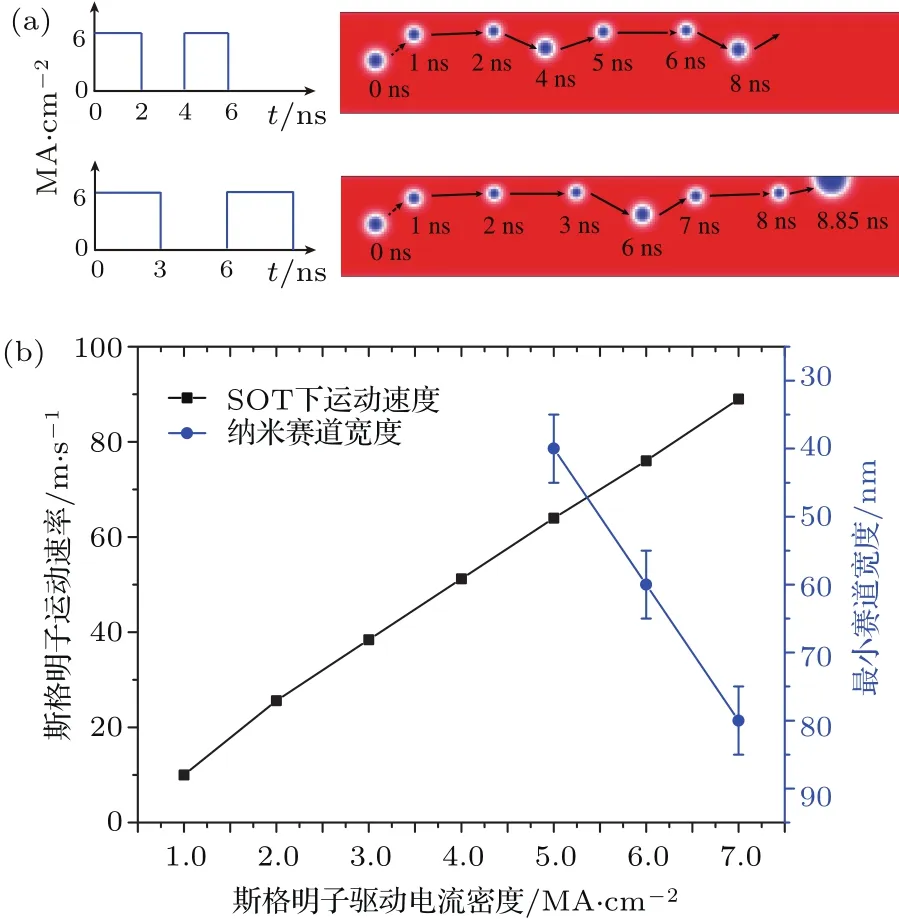
图8 (a)在受限纳米线中,过大的驱动电流会使得斯格明子在纳米线边界处发生湮没,但是通过采取脉冲驱动电流,并采取合适的脉冲宽度和间隔,可以有效避免这一情况的发生;(b)斯格明子在纳米线中迁移速率与驱动电流密度呈现正比关系,但随着驱动电流的增大,为保证斯格明子不在边界处湮没,纳米线的最小宽度也随之增大,器件的信息传输速率(斯格明子迁移速率)与面积(纳米线宽度)之间存在竞争关系Fig.8.(a)In constricted geometry,skyrmions will be annihilated in the edge due to the large driven current.By using pulse current with certain duration and interval,this annihilation of skyrmions can be prevented;(b)the moving speed of skyrmions is directly proportional to the driven current density.However,with a larger skyrmion moving speed,a larger minimum width of the nanotrack is also required.In other words,the speed and the area of the device is a trade o ff.
除了电流外,斯格明子还可以被温度梯度[131,132],磁场梯度[133],自旋波[134−136],电场等[104]方法驱动.理论研究已经证明自旋波能够有效地驱动斯格明子.通过在纳米线的一端施加振荡的磁场,可以在纳米线中激发出沿纳米线传播的自旋波.斯格明子将会随着自旋波而发生输运,如图9(a)所示[101,134].该方法在理论上由于没有电流所产生的热损耗将具有更低的能耗.但是,由于产生自旋波需要外界磁场,在真正的器件设计中不如电流驱动实用.类似的还有利用应力控制的斯格明子[137],通过应力能够改变材料结构中对应的磁学参数,从而达到控制斯格明子的产生及输运.
近期还出现了一种新型的利用交替变化的电压控制磁各向异性驱动斯格明子的方法.斯格明子在具有梯度势能的纳米线中会向低势能区域移动.这种移动方式具有高效且无侧向位移的优势.通过电压控制的垂直磁各向异性(perpendicular magnetic anisotropy,PMA)能够人为地改变纳米线局部区域的势能分布.利用这一特性可以使得斯格明子始终处于一个梯度势能中,从而利用电压使得斯格明子产生输运[138].其具体的器件设计犹如磁悬浮列车轨道,前后电极交替变化,如图9(b)所示.相对于之前所介绍的电流驱动方法,这一全新的驱动模式已经被理论证明可以在大幅度降低功耗(约3个数量级)的同时实现斯格明子的高速移动(259 m/s)[139].
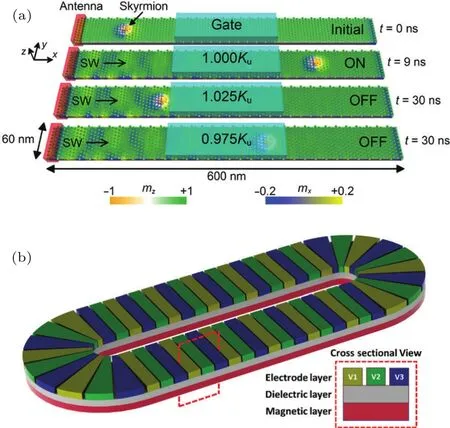
图9 (a)利用微波天线可以在铁磁纳米线一端产生沿纳米线传播的自旋波,从而驱动斯格明子运动;(b)通过相邻的多个VCMA门可以在纳米线中产生随斯格明子位置连续变化的能量梯度,驱动斯格明子前进[138]Fig.9.(a)Skyrmions can be driven by spin waves generated by a microwave antenna in one terminal of the track;(b)controlling the anisotropy gradient by multiplexed gate architecture to drive skyrmions effectively[138].
尽管上述非电流驱动的方法在理论上具有更低的能耗,但是目前的研究仍然处于理论阶段,亟待实验验证.因此,目前斯格明子电子学中主流的驱动方法仍然是电流驱动.
5.3 斯格明子的检测
斯格明子可以通过拓扑霍尔效应(topological Hall effect,THE)[25,140,141]或者磁阻效应进行检测(magnetoresistance)[90,142−148].2009年,Neubauer等[25]通过THE检测的方法测量了MnSi中的A相(即后来的斯格明子相),证明其包含一种拓扑量化的贝瑞相.但是这种方法难以用于电子器件中.因此,在电子器件设计中一般采取磁阻的方法检测斯格明子.人们最先想到的是利用斯格明子导致的霍尔电阻的变化.在一诸如纳米线的受限结构中,纳米线两端导线的霍尔电阻值与纳米线中磁矩分布密切相关.当斯格明子通过时,由于磁矩的改变,纳米线两端霍尔棒(Hall bar)所测到的霍尔电阻将随之变化.通过观察霍尔电阻的变化,即可以探测到斯格明子的存在[143],如图10(a)所示.另外一种方法是利用MTJ中的隧穿磁阻变化.由于MTJ的隧穿磁阻取决于自由层中的磁矩方向,当斯格明子运动到由MTJ构成的读取头下方时,磁矩方向的改变会导致与自旋有关的电子态发生改变,从而使得MTJ隧穿磁阻发生变化.通过读取该阻值的变化即可判断出读取头区域是否存在斯格明子,如图10(b)所示.理论上来说,该方法可以取得高达20%的磁阻变化范围[142].利用这一原理,仅仅依靠简单的垂直磁性器件实现全电学的斯格明子探测将成为可能.
除了隧穿磁阻效应外,另一种可以用来探测斯格明子的磁阻效应被称为各向异性磁阻(anisotropic magnetoresistance,AMR).这一效应源自于由自旋轨道耦合引起的材料内禀属性,但是其能够实现的阻值变化相对较小,难以应用于斯格明子电子器件中[148,149].近年来,又出现了一种全新的通过电学手段实现斯格明子探测的方法,即非共线型磁阻(non-collinear magnetoresistance,NCMR),如图10(c)所示.由于斯格明子的磁矩在空间具有连续变化,因此斯格明子的不同部位具有不同的隧穿磁阻,并引发一种激烈的电流.从结果上看,斯格明子在电学上与铁磁背景发生了明显的区别.实验中,Hanneken团队[145]运用这一原理通过STM成功地探测了Pd Fe/Ir(111)中的单个斯格明子.
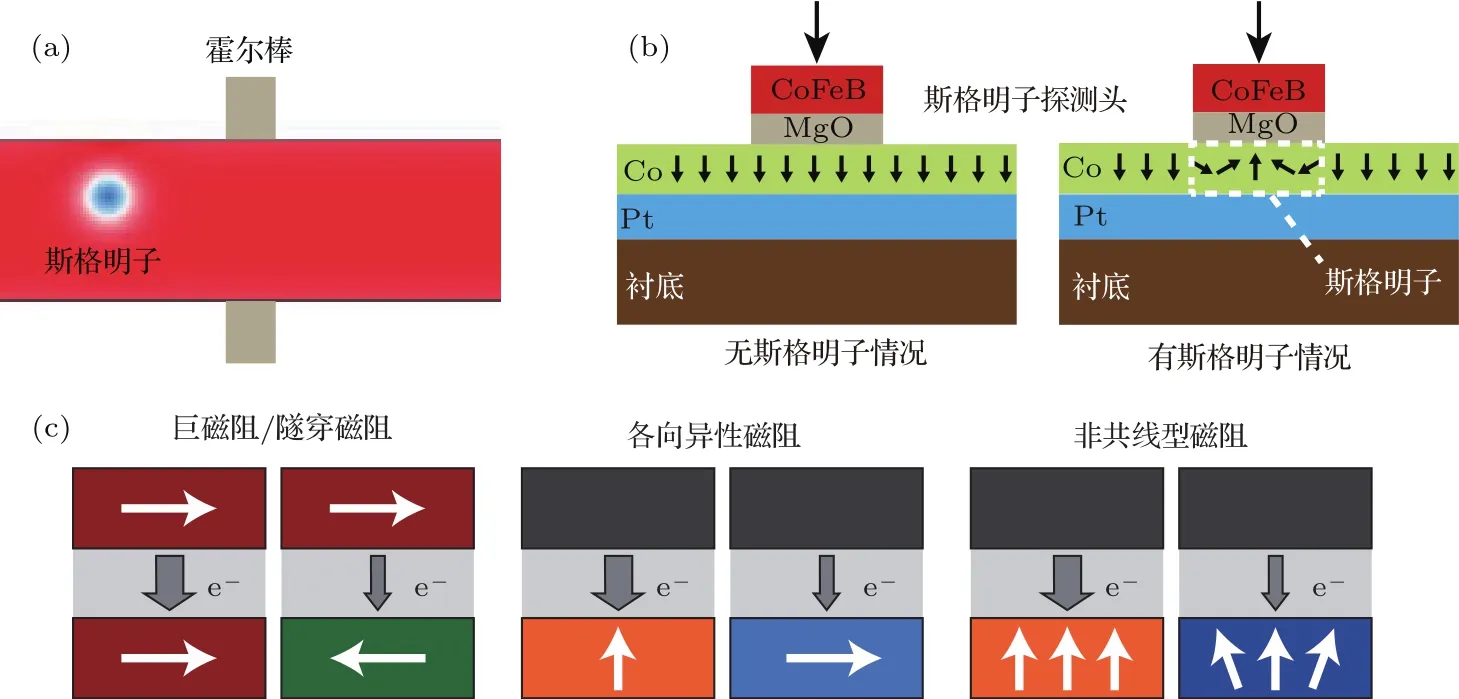
图10 斯格明子可以通过(a)霍尔棒或(b)垂直异质结结构进行探测;(c)对于异质结结构的探测方法主要可以通过GMR/TMR,AMR及NCMR三种效应实现Fig.10.Sky rm ions can be detected by(a)Hall bar and(b)perpendicular hetero junction;(c)three effects:the GMR/TMR,AM R,and NCMR can be used in the detection of skyrmions by hetero junction.
5.4 斯格明子的调控
斯格明子无论是作为存储器件还是逻辑器件中的信息载体,对其有效的操作方法都是必不可少的,即可通过电学的方法控制斯格明子的运动方向和运动速度.理论研究表明,通过人为地控制器件中的能量分布可以实现对斯格明子的控制.例如通过在纳米赛道中加入温度梯度,可以实现对斯格明子霍尔角的有效调控[150].通过电压控制的磁各向异性(voltage-controlled magnetic anisotropy,VCMA)效应,提高或者降低器件某一区块的磁各向异性能,从而实现斯格明子的钉扎或者通过.这一想法已经在理论上获得了验证[100,151],如图11(a)所示.DE代表电极层,FM代表铁磁层,HM代表重金属层,在VCMA门电极上施加正偏置电压,形成一个能量势垒,将能够有效地钉扎斯格明子.根据这一结论,可以设计出诸如斯格明子晶体管、赛道存储器等多种相关器件,将在下文器件介绍部分进行详细阐述.Wang团队[129]更进一步地将VCMA门设计为不规则形状,研究了电压控制的斯格明子在人工设计路径上的输运,为斯格明子器件的进一步设计奠定了基础,其设计如图11(b)所示.通过VCMA提高不规则区域的磁各向异性,形成一个人工控制的不规则低能量轨迹.在电流驱动下,斯格明子将沿着该可控轨迹运动.

图11 (a)通过电压控制的磁各向异性钉扎斯格明子;(b)通过VCMA控制形成一不规则低能量路径,在电流驱动下,斯格明子将沿这一路径运动Fig.11.(a)Depinning of skyrmions by voltage controlled magnetic anisotropy;(b)skyrmions can be constricted in a curved path by the control of VCM A.
6 斯格明子电子器件概念及详细介绍
随着对斯格明子性质的深入研究,将斯格明子作为信息载体展现出了十分明显的优势,包括高存储密度(尺寸小)、高灵敏度(驱动电流阈值小)、高可靠性(结构稳定).因而,基于斯格明子的一系列信息器件设计被相继提出.其应用方向主要分为存储、逻辑以及类脑等3个方面,如图12所示.接下来我们将举例介绍相关的斯格明子器件设计.
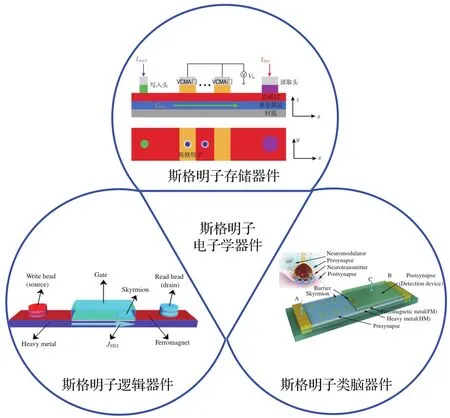
图12 斯格明子电子学器件的主要应用方向有3个方面:1)存储器件;2)逻辑器件;3)类脑器件Fig.12.Sky rm ionic devices can be applied in three aspects:1)Storage devices;2)logic devices;3)neuromorphic devices.
6.1 斯格明子存储器件
斯格明子存储器主要分为基于MTJ的单结多值存储以及基于赛道的立体存储设计.研究发现,在空间受限的磁体结构中,能够可控地产生或者湮没一到数个斯格明子.2015年,田明亮团队及其合作者[90]通过改变外加磁场测量到了MnSi纳米线中由于斯格明子产生及湮没所导致的磁电阻跳变.我们将这一现象推广到MTJ中,仿真证明了利用电流所产生的STT在MTJ钉扎层漏磁场的辅助下可以可控地在其自由层中产生或是湮没斯格明子,从而获得一个多值的磁阻变化[152].该设计可以作为一种单结的多值存储单元,实现高密度存储,同时将可能应用于人工神经网络.
另一方面,基于DW的赛道存储器(racetrack memory,RM)设计早在2008年就被Parkin等[153]所提出.在DW-RM中,一系列被DW所分隔的向上或是向下的磁畴(magnetic domain)代表了二进制信息中的“0”或是“1”.在电流的驱动下,DW可以在纳米线中发生输运,从而传递磁畴中所存储的信息.因此,赛道存储器被认为有希望取代硬盘作为大规模存储应用.但是同时,利用DW作为赛道存储器信息载体存在一些潜在的问题,例如,所需的驱动电流阈值过大,易受到材料缺陷的影响被钉扎等.这些缺陷极大地限制了DW-RM的发展,使其至今只能停留在理论层面.斯格明子的出现正好弥补了利用DW设计赛道存储器的不足,将有希望成为新的赛道存储器信息载体.
首先,我们设计了一种基于斯格明子的赛道存储器[154].在这一设计中,二进制信息“0”或是“1”被编码为具有不同间隔距离的一长链的斯格明子.由于斯格明子相较于DW-RM中的磁畴具有小得多的尺寸,在相同器件面积下,斯格明子将能够具有更高的信息存储密度.更进一步,斯格明子相较于DW的驱动电流阈值小5—6个数量级,具有更好的控制灵敏度,同时也降低了器件的运行功耗.除此之外,斯格明子所具备的拓扑保护属性使得编码于斯格明子序列中的信息更加鲁棒.在器件存在缺陷的情况下,斯格明子仍然能够克服缺陷传递信息,而不会像DW一样发生钉扎或是破裂而丢失信息.
典型的斯格明子赛道存储器结构如图13所示,其主要由写入头、纳米赛道、读取头三个部分组成.写入头可以产生斯格明子:如事先定义一个斯格明子代表信息“1”,没有斯格明子则代表信息“0”,根据所需写入的数据“1”或者“0”,写入头可以产生或者不产生斯格明子.每一个时钟周期,纳米赛道中均会产生一个恒定大小和持续时间的“时钟”驱动脉冲,在这一脉冲驱动电流作用下,已经被写入的斯格明子会沿着纳米赛道依次传递,从而形成一个包含有效信息的斯格明子序列.这一序列在经过读取头时,读取头将利用前面所述的探测方法探测当前比特位是否存在斯格明子,从而将储存于斯格明子序列中的有效信息提取出来.目前这一概念在实验上已经得到一些初步的验证[155].由于斯格明子的产生、驱动、探测方法均已经在前面讨论,不再赘述.斯格明子赛道存储器将这三部分结合在一起,从而形成一个完整的信息储存器件,是斯格明子电子学领域的基础应用之一.
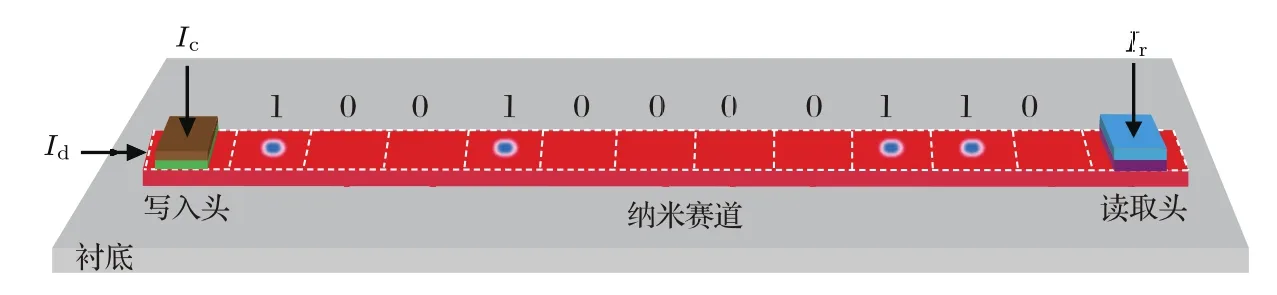
图13 将斯格明子作为信息载体的赛道存储器示意图,其主要组成部分为写入头、纳米赛道以及读取头Fig.13.Schematic diagram of the nanotrack devices using skyrmions as in formation carriers.This device has three main components:the writing head,the nanotrack,and the reading head.
在斯格明子赛道存储器的实际设计中,还需要考虑一些具体的问题.我们考虑的第一个问题是在作为一个序列传递的过程中数据不会出现错位.由于斯格明子的运动和DW运动类似,在实际过程中其运动快慢受到外部诸如温度、非均匀的材料晶粒等影响可能会偏离实际预期,从而发生数据的错位.为了解决这一问题,我们需要斯格明子序列中的所有斯格明子在每一次受电流驱动时所运动的距离保持一致.考虑到斯格明子会被高能量势垒钉扎,利用电压控制的VCMA可以人为地产生可控的磁各向异性能量势垒,实现对纳米赛道中斯格明子的钉扎/通过控制,即形成一个可开关的门(gate).将每一个比特位用这样的VCMA门分隔,如图14所示.只有当需要斯格明子通过的时候打开,当需要写入或者读取斯格明子的时候则关闭门[100].这样的设计使得整个斯格明子序列按照比特位步进式地传递,避免了斯格明子因为运动过快或者过慢导致的错位.
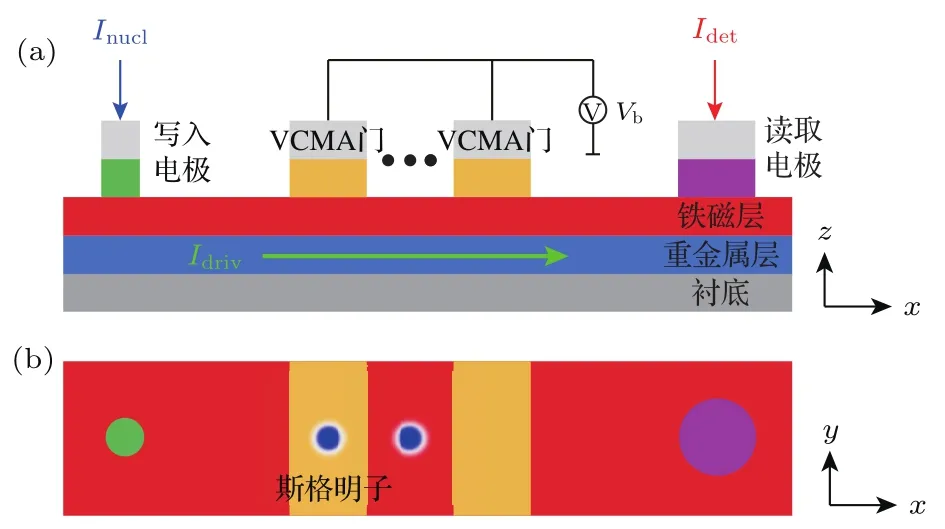
图14 VCM A控制的斯格明子赛道存储器 (a)横截面及(b)顶层示意图Fig.14. The schematic diagram of the VCMA skyrmionic racetrack memory.
另一个问题来自斯格明子读取中可能出现的错误.在DW-RM中,磁畴的方向决定了存储的信息,非“0”即“1”.但是在斯格明子赛道存储器中,有斯格明子代表“1”,铁磁背景代表“0”.如果读取端在读取斯格明子时并未恰好检测到斯格明子则会导致读取错误.此外,在信息同步中连续的“0”有可能使得数据发生失锁的现象.为了克服这些问题,我们设计了一种采取差分方式编码数据的结构[156],如图15(a)所示.在这一设计中,我们采用首端相连通的两条平行的纳米赛道L和R表示同一组数据.这两个纳米赛道首端均有一个可控的VCMA门,可以将斯格明子阻断在赛道外或是允许其进入.在每一个时钟周期写入端均产生一个斯格明子.根据所需写入数据的不同,选择打开或者关闭相应的赛道.例如,定义数据“1”为R赛道中的斯格明子,而“0”为L赛道中的斯格明子.当需要写入“1”时,打开R赛道,同时关闭L赛道,则斯格明子将进入R赛道形成一个数据“1”,如图15(b)所示.读取时,需要对比R和L赛道中的磁矩状态,进行差分.假设某一赛道中斯格明子序列发生了偏移,则会在读取时出现两个赛道同时有或是没有斯格明子的情况,系统可以立即发现并进行纠正.因此,这一设计可以极大地增强赛道中数据的鲁棒性,减小差错率.同时,由于始终能够在某一个赛道中探测到斯格明子,即使是连续的“0”或者“1”数据也不会导致失锁现象的发生.最后,由于读取数据采取了差分的方法,相对于读取单个赛道中斯格明子其电阻变化范围更大,提高了读取的灵敏度和可靠性.当然,这一设计也存在诸如信息密度降低等问题,是利用器件所占芯片面积换取数据可靠性的一种取舍.
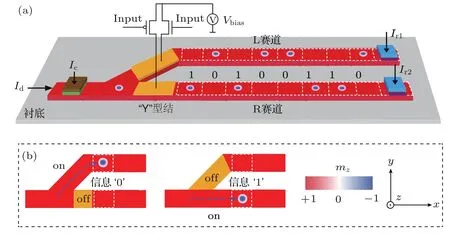
图15 采用差分编码的斯格明子赛道存储器结构(a)示意图及(b)工作方式示意图Fig.15.Schematic of the complementary skyrmion racetrack memory.
6.2 斯格明子逻辑器件
2015年,一种基本的逻辑器件——晶体管,被理论证明可以利用斯格明子实现[151].其具体的器件设计如图16(a)所示.一个VCMA门被置于器件的源极和漏极之间作为斯格明子晶体管的控制门.源极由一个置于纳米线上的MTJ组成,能够在垂直极化电流的激发下产生斯格明子.斯格明子在源极产生后会受到纳米线中电流或者自旋波的驱动向漏极运动.VCMA门所在区域的PMA会受到局部电场E的调控,其大小可以用(18)式表示[157,158]:
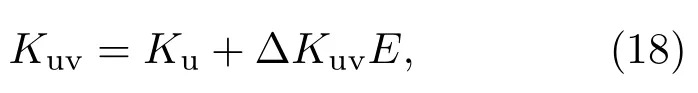
其中Kuv与Ku分别表示经过VCMA门调节之后与之前的PMA常数,∆Kuv为与VCMA强度相关的一常量.这一线性表达式已经在实验中被Shiota团队[159]所证实.
由于PMA的改变,该区域内总能量会随之变化,从而形成一个能量势垒,阻挡斯格明子继续向漏极运动.斯格明子的能量可以表述为[151]
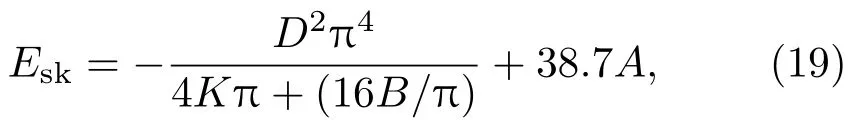
其中D为DMI系数,K为PMA常量,A为交换相互作用常数,B为磁场强度.由(19)式可知,当PMA增加时,斯格明子的能量随之增大,反之,斯格明子的能量随PMA减小而减小.如图16(b)和图16(d)所示,假设通过VCMA门的调节,门区的PMA增大(Kuv=1.05Ku),则对于斯格明子来说会形成一个能量势垒,斯格明子会被钉扎在势垒的外侧;而当VCMA门使得区域PMA减小时(Kuv=0.95Ku),如图16(c)和图16(e)所示,则会相应地形成一个斯格明子的势井,斯格明子在通过这一势井时会陷入其中,被钉扎于势井内侧.另外,斯格明子是否会被钉扎在VCMA门控制区域还取决于驱动斯格明子的电流密度.因此,对于斯格明子晶体管来说,存在两种控制方法.一种方法是在源极与漏极之间通过恒定的电流,使得斯格明子始终受到指向漏极的驱动力,如图16(b)和图16(c)所示.通过控制VCMA门的开关,可以选择将斯格明子钉扎在源极,或者使其到达漏极,实现晶体管的开关功能.另一种方法则是保持VCMA门区域的PMA不变,形成一个固定的势垒或者势井.在一个较小的电流的驱动下,斯格明子会被钉扎在这一势垒或势井中.需要斯格明子通过时,加大电流密度,使其跨越势垒(井),到达漏极,如图16(d)和图16(e)所示.
另一方面,周艳团队利用斯格明子可以和DW相互转换的特点[105],提出了一种利用斯格明子实现逻辑门的设计[43].如图17所示,通过控制纳米线的宽度,即可实现逻辑中常见的OR或者AND门.在较窄的纳米线中,无论输入端是一个斯格明子或者同时都有一个斯格明子,在纳米线中均会转化为完整的DW,进而进一步得到一个完整的斯格明子,实现逻辑上的OR.在较宽的纳米线中,只有当两个输入端同时输入一个斯格明子时才能产生一个完整的DW,在输出端得到一个斯格明子;如果只有一端有斯格明子,其转化为的DW将不足以占据整个纳米线,从而形成一个会湮没于纳米线中的不完整DW,由此实现逻辑上的AND.
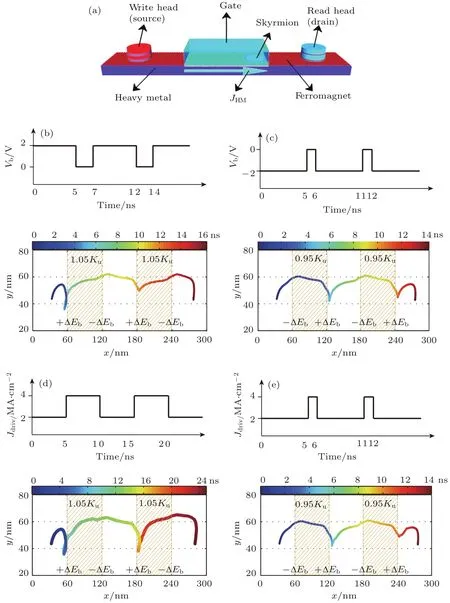
图16 (a)斯格明子晶体管示意图;(b)—(e)利用改变驱动电流或者VCMA门电压控制斯格明子的运动Fig.16.(a)Schematic diagram of the skyrmion transistor;(b)–(e)manipulation of skyrmion motion by control of the driven current and VCM A gate.
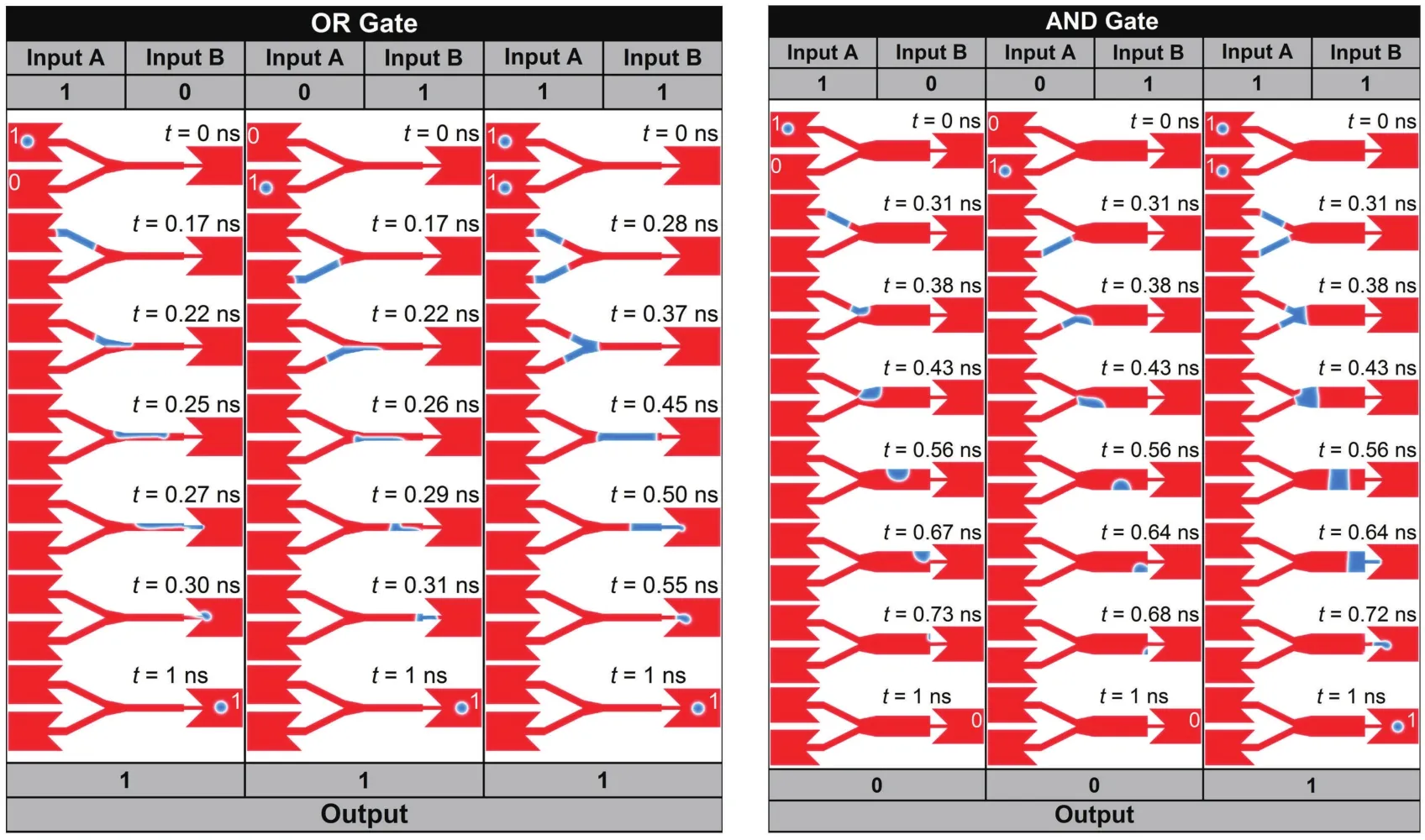
图17 基于斯格明子与磁畴壁转换设计的逻辑“或门”(左)及“与门”(右)[43]Fig.17.“OR”and “AND”gate based on the conversion between skyrmions and domain wall pairs[43].
6.3 斯格明子类脑器件
相较于传统的利用磁畴(例如硬盘)或是电荷(例如闪存)作为信息载体的器件,斯格明子信息具有其独特的特点.首先,斯格明子是一种可编码的类粒子结构,复数的斯格明子可以自然地聚集在一起形成多进制的信息,并且通过斯格明子个数不同所导致的磁化分布不同进行区分.其次,由于斯格明子受电流驱动的运动完全可控,使得该多进制信息与驱动电流紧密相关.最后,斯格明子由于其粒子特性,当多个斯格明子聚集在一起时每一个斯格明子的位置具有一定的随机特性.上述“多值”,“可控”以及一定的“随机性”特点使得斯格明子更加适合于神经网络相关应用.
根据以上特性,我们设计了一种基于斯格明子的神经突触[45],如图18(a)所示.该设计的基本组成部分为突触前级和突触后级,两者均处于同一纳米线铁磁层薄膜,被中间具有高PMA的能量势垒所隔离.在突触前级中,利用DW转化等手段使得突触前级斯格明子数量达到饱和.由于纳米线中心能量势垒的阻挡,所有的斯格明子都被限制在突触前端,形成该突触的初始状态.当正/负向的外部的激励(电流)到达时,斯格明子受到电流的驱动跨越能量势垒到达/离开突触后级,其到达/离开的斯格明子个数完全取决于器件所受激励的大小和时间长短.突触后端的整个区域被作为读取区,利用MTJ或其他磁性探测器可以探知该区域的磁矩变化,并以磁阻的形式反映出来.定义该磁矩为整个突触器件的权重,从上述工作过程可知,外部激励在通过斯格明子突触后会改变斯格明子在突触后级分布的数量,从而改变器件权重的大小,即实现了神经突触的可塑性(plasticity)功能.
进一步的研究发现,这一器件设计还同时满足了神经突触中的短时程突触可塑性(short-term plasticity,STP)以及长时程增强(long-term potentiation,LTP)功能,如图18(b)—(e)所示.假定器件中所有激励电流具有相同的大小,如图18(b)所示,在情况1中,激励具有1.5 ns的持续时间和5 ns的间隔,此时,斯格明子有足够的时间在激励消失前越过势垒,形成LTP;保持激励的频率,减小持续时间到1 ns(情况3),这一情况下,斯格明子无法有效地翻越势垒,当激励消失后器件完全返回到激励到达前的状态,形成STP,如图18(d)所示;保持1 ns的激励持续时间,将激励的频率提高为间隔2 ns,如图18(c)情况2所示,此时虽然单个的激励无法使斯格明子越过势垒,但由于间隔较短,下一个激励在斯格明子完全返回初始状态前到达,在跨越势垒的能量上形成了积累.斯格明子在多个激励作用下最终跨过势垒,改变了器件权重,形成LTP.由此可见,激励的持续时间和频率决定了器件发生STP或是LTP,与神经网络中突触的设计相符.这一器件设计是第一次将斯格明子运用于神经网络器件,为后续的相关应用打下基础.
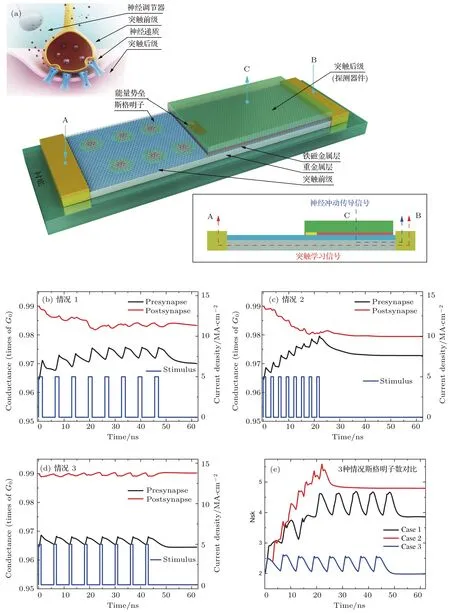
图18 (a)斯格明子神经突触结构示意图,该器件首次利用斯格明子的可聚集特点实现了人工神经突触的(d)STP及(b),(c)LTP功能Fig.18.(a)Schematic diagram of a skyrmionic synapse.This device is designed based on the(d)short-term plasticity(STP)and(b),(c)long-term potentiation(LTP).
继斯格明子神经突触之后,我们又提出了基于斯格明子的神经元设计,如图19(a)所示[46].该设计利用了斯格明子在梯度PMA分布的纳米线上会自发地向低能量端运动的特点,模仿神经元中的漏-收集-激发(leaky-integrate- fir,LIF)模型.该模型的具体描述可以理解为神经元所同时具有的三种功能,如图19(c)所示:能够随时间恢复原始状态(漏),能够收集前端神经元所发出的激发信号(收集),以及可以在收集信号达到阈值的时候产生一个激发信号(激发).
整个器件的铁磁层被设计为具有梯度变化的PMA.在PMA较低的一端(写入端)有斯格明子的产生单元,在PMA较高的一端(读取端)为斯格明子的探测单元.斯格明子由产生单元生成后由于受到纳米线上梯度能量分布的影响,会趋向于保持在能量较低的写入端.当由前级神经元产生的激发信号传入当前神经元时,斯格明子会受到电流的驱动向具有较高能量的读取端运动.在我们的设计中,单个的激励信号并不能使斯格明子到达读取端,斯格明子将会停在某一中间位置.梯度能量分布使得斯格明子将自然地向低能量的写入端回落,即形成了LIF模型中的“漏”.假如在斯格明子完全回到初始位置之前,神经元接收到了另一激发信号,则斯格明子将再一次向读取端运动,其达到的位置不仅仅反映了当前的信号,还积累了部分之前信号的贡献,即LIF模型中的“收集”功能.最后,当积累的信号达到某一阈值,斯格明子将到达读取端,并通过探测单元向后端输出一激发信号,完成LIF模型中的“激发”.这一设计巧妙地利用了斯格明子的物理特性,将原本复杂的电路功能在一个简单的器件中实现,证明了斯格明子在神经网络领域的潜在应用价值.
采取类似的思路,将纳米线宽度设计为线性变化,利用纳米线两端线性变化的排斥力代替由梯度PMA导致的线性排斥作用,实现同样的LIF功能[47,128].相对于实现梯度PMA,在实验和器件制备中改变纳米线宽度更加具有可操作性.我们由此设计了一种基于该原理的新型人工神经元器件[47],如图19(b)所示.为了抵消斯格明子霍尔效应,该器件被设计为双层铁磁层耦合结构[130].当受到电流作用产生运动时,斯格明子所受到的纳米线边界的作用力会随着其位置的变化而逐渐增加,从而产生符合LIF模型的运动模式,如图19(d)所示.
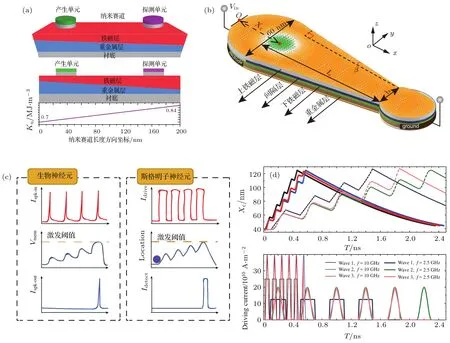
图19 (a)基于PM A变化及(b)纳米线宽度变化设计的斯格明子神经元器件示意图;(c)斯格明子神经元所实现的LIF功能信号与生物神经元信号对比;(d)不同激发信号下斯格明子在宽度变化纳米线中的位置变化Fig.19.Schematic diagram of skyrmionic neuron based on controlling(a)PMA and(b)the width of nanotracks;(c)comparison of LIF signals from skyrmionic neurons to biological neurons;(d)the position change of a skyrmion in the wedged width nanotrack under different input current pulses.
7 斯格明子电子学未来的发展
7.1 当前斯格明子电子学所面临的问题和挑战
斯格明子凭借其特殊的拓扑性质以及所对应的尺寸小、易驱动、结构稳定等优点,被认为是未来自旋电子器件中的理想信息载体.自2009年首次在实验中被发现以来,关于斯格明子性质及其应用的研究便成为学术界关注的热点.但是在其实际应用的过程中仍然存在一些亟待解决的科学及技术问题.
1)斯格明子器件的微纳电子器件集成
如前所述,至今斯格明子作为信息载体所需要的写入、操作及读取等功能都已经独立地在实验中得到证实.但是,这些实验有的需要在低温下进行,例如Wiesendanger团队[103,145]利用STM观测斯格明子并对其进行读写的实验,有的则是研究斯格明子阵列[160,161].近年来,室温下的斯格明子在多种材料结构中被发现[33,36,83],但是仍然依赖于LTEM,MFM等外部实验设备进行成核及探测.未来的一大挑战将是把单个斯格明子的产生、输运及探测利用电学的方法在室温下实现,并集成到同一个微纳电子器件中.
2)可实际应用的材料/结构体系
当前研究最广泛的斯格明子材料体系,无论是斯格明子阵列还是单个的斯格明子,都局限于具有中心反演对称性破缺的B20型体材料或是具有手性的铁磁薄膜,例如MnSi等[24,26],FeCoSi[28,42],Cu2OSeO3[162]DM相互作用来自于材料体效应的体系,或是Pt/Co等[34],Ta/CoFeB[36],Fe/Ir[27,103]由于多层薄膜不同层之间非对称产生的界面DM相互作用体系.其中只有一少部分是能够在室温下稳定获得斯格明子的体系,并且尚面临产生的斯格明子尺寸过大或是难以被驱动的问题.另一方面,斯格明子虽然在理论上能够克服材料中的缺陷进行输运,但实验发现材料缺陷对斯格明子实际上具有明显的钉扎作用[34].因此,适用于斯格明子器件的材料体系在满足室温稳定存在斯格明子的同时,还应具备较高的薄膜质量.近期研究表明,非晶铁磁薄膜或许将能够解决薄膜质量问题,例如非晶的Ta/CoFeB/MgO被发现优于具有晶体结构的Pt/Co/Ta结构[163,164].在斯格明子输运方面,当前斯格明子器件的设计多依赖于电流驱动的斯格明子输运.为了降低驱动电流密度,需要材料具有更大的自旋霍尔角.改变材料的自旋霍尔角往往会附带地改变其他诸如DM相互作用、垂直各向异性等参数.综合考虑这些参数也是对当前材料体系的一大挑战.最后,考虑到相关器件的电流电压控制仍然依赖于现有的半导体工艺及器件技术,因而斯格明子电子学所采用的材料体系还需要考虑与之相兼容.
3)斯格明子的高效输运
斯格明子的输运相较于DW具有极低的阈值电流密度.但是,在信息传输等希望获得较高输运速率的情况下,斯格明子的输运速率与DW相当.前文所介绍的采用变化电压驱动斯格明子的方法可以在极低功耗下获得高速的输运[139],但仍然亟待实验的论证.此外,由于斯格明子霍尔效应的存在,斯格明子在受限纳米线中运动会发生一个垂直于纳米线的偏移[31,122].这不仅在一定程度上降低了斯格明子的运动速度,还限制了其所能取得的最大输运速率.如图7(b)所示,在大电流密度下,纳米线边界将不足以提供足够抵消斯格明子霍尔效应的排斥力,进而使得斯格明子发生湮没.一种解决方案是利用反铁磁耦合的双层铁磁薄膜代替原设计中的铁磁层[165].由于上下两层中所产生的马格努斯力完全抵消,斯格明子运动过程中将不会产生霍尔偏移.另一种方案则是在纳米赛道两端添加防止斯格明子破坏的能量势垒[166].上述方法在理论上均能取得较好效果,因此能够从实验中检验这些新方法将是未来的研究热点之一.
7.2 斯格明子电子学未来的应用前景
斯格明子有望将拓扑保护这一全新特性带入器件设计领域,并带来许多全新的能耗和性能上的突破,其应用前景主要体现在下述三个方面.
1)提升自旋电子存储器件的性能
斯格明子小尺寸的特点意味着在相同芯片尺寸的情况下可以存储更多的信息.同时,更低的启动电流密度和电压控制的方法使得其信息操纵更加方便灵活,甚至可以实现aJ/bit量级的超低功耗[139].拓扑保护的特点则决定了斯格明子可以作为稳定信息比特长时间存储.由此,斯格明子将有望实现自旋电子器件中的信息存储单元在可靠性、速度、存储密度等方面的全面提升.
2)构建新型结构及功能自旋电子器件
斯格明子在各种外力作用下的运动模式都已经被广泛研究,包括自旋极化电流的影响[32]、纳米线边界的影响[64]、斯格明子之间的相互作用[123]、铁磁材料能量分布的影响[129]等.利用上述研究成果,斯格明子的运动轨迹已经可以在理论上被精确控制,从而设计出一些替换传统器件中需要复杂结构才能实现的功能.例如,利用斯格明子运动特点可以设计出具有高频稳定的信号发生器[167];传统的数据插入需要移动整个数列中所有数据,而斯格明子所代表的数据则可以利用一个边路的纳米线自然地实现[168];可编程的逻辑器件也可以利用控制斯格明子的位置来更有效地实现[44].
3)利用斯格明子的类粒子特点可以实现仿生器件
斯格明子的另一特性是作为类粒子结构,复数的斯格明子可以自然聚集在一起表示一个多值的数据.例如前文介绍的斯格明子神经突触[45]即是利用斯格明子个数的变化表达突触权重.利用这一特点,斯格明子作为信息载体将有效地突破二进制冯·诺依曼体系的限制.在未来将有望实现多值、逻辑存储相结合的新型器件突破.
8 总 结
本文回顾了斯格明子的发现过程及其拓扑特性、器件应用等方面的研究现状,探讨了相关自旋电子器件的应用前景,并对当前所遇到的问题进行了讨论.着眼于将斯格明子应用于电子器件及集成电路,即斯格明子电子学,本文重点讨论了斯格明子的电学写入、控制及读取功能;详细介绍了斯格明子存储、逻辑及类脑计算器件.在这些设计中,斯格明子作为信息载体使得一些原本复杂的操作被极大地简化,无论是功耗还是性能都得到了相应的提升,展现出其在后摩尔时代的应用潜力.尽管如此,斯格明子电子器件离实际应用尚存在一些亟待解决的基础科学及技术问题,需要在材料结构设计、控制方法及微纳集成技术等方面开展进一步深入的研究.

