基于增广拉格朗日方法的电动汽车聚合商分散充电控制策略

赵小波, 严 正，冯冬涵，许少伦

(1.上海交通大学电气工程系，上海 200240；2.上海交通大学电力传输与功率变换控制教育部重点实验室，上海 200240)

0 引 言

电动汽车技术的发展是解决气候变化、能源危机和环境污染问题的有力措施。大量电动汽车接入电网，将对系统运行造成影响。相比于传统的电力负荷，充电负荷可控性更大。因此，对电动汽车的充电过程进行有序控制有利于减小电动汽车接入电网所产生的不利影响，提高电网供电可靠性以及资源利用效率[1]。

一般而言，电动汽车充电控制策略可以分为集中充电控制策略[2-4]和分散充电控制策略[5-8]。在集中充电控制策略中，控制中心接受下辖所有电动汽车的充电需求信息，集中求解充电方案并下发到各电动汽车智能充电单元。目前，集中充电控制策略已经有较多研究成果。如文献[3]以最小化配网网损为目标，提出了一种集中充电控制方式协调电动汽车的充电过程。文献[4]研究了一种以分时电价机制下充电站的运营收入最大化为目标的集中充电控制策略。与集中充电控制不同，分散充电控制策略不需要由控制中心统一计算充电方案，而是通过控制信号的传递实现电动汽车充电方案分散求解。电动汽车急剧增多，相比较于集中充电控制策略，分散充电控制策略更有优势，具体表现在求解速度更快、效率更高、通信量更小以及信息更加安全等方面，因此有较大的研究意义和实际价值，且形成了不少创新性的研究内容。文献[5]将多代理智能体应用到电动汽车分散充电机制设计中，以最小化峰谷差为目标进行电动汽车充电行为的协调，但最优性和收敛性难以保证。文献[6]以削峰填谷为目标，提出了一种分散最优算法(ODC，optimal decentralized charging)，并从理论上证明了该方法的正确性和可行性，仿真结果显示了良好的性能，但未对系统安全约束进行讨论。文献[7]结合方差成本和节点电价，基于需求响应模型设计了一种分散充电优化策略，但其有效性依赖于需求响应模型的精确度。

电动汽车聚合商[9](以下简称聚合商)作为电网和个体电动汽车之间的中介，参与电动汽车的管理。可以预见，未来聚合商管辖的电动汽车数量将会不断增长，但针对聚合商的分散充电控制策略尚缺乏研究。本文在当前研究的基础上，提出了一种基于增广拉格朗日方法的分散充电控制策略。该策略实现了聚合商对下辖电动汽车充电行为的分散控制，可有效处理配电网安全约束，并使聚合商利益达到最大化。

1 聚合商集中充电控制模型

本文研究场景设定如下：某一配电网下的电动汽车用户与聚合商签订合同，由聚合商为用户建设充电桩、通信网络等基础设施并提供一定的电池维修、更换服务，以此为条件来对电动汽车进行充电控制[4]，在控制过程中需要保证电动汽车充电需求得到满足。

1.1 聚合商充电控制目标函数

借鉴文献[4]，电动汽车聚合商是电动汽车充电服务的提供者，按照充电服务价格向电动汽车用户收取充电服务费用，按照分时电价向售电公司支付电费，以两者的价差实现盈利，其目标函数如下：

(1)

式中：下标j表示节点的编号;t表示控制时段的编号；i表示电动汽车的编号；Nd为配电网下接入电动汽车的节点数；T是控制总时长，本文中设置为1d；Nj为节点j下接入的电动汽车的集合；Pei,t为电动汽车i在时段t的充电功率；Δt为控制时间段的时长，本文取为15min；c为聚合商向用户收取的充电服务电价；φt为时间段t内的分时电价。目标函数(1)等价于：

(2)

1.2 聚合商充电控制约束

1.2.1电动汽车充电约束

①电池电量状态(SOC，state of charge，电池电量占电池容量的百分比)约束。

SOCi,e≤0.95

(3)

SOCi,e≥SOCi,s≥0.2

(4)

式中：SOCi,e为电动汽车i的结束时期望电池充电状态;SOCi,s为电动汽车i的起始时电池电量状态。式(3)表明电动汽车用户结束时期望电池充电状态的最大值为0.95。式(4)表明为防止深度放电，一般要求电池电量状态不低于0.2。

② 充电功率和电量约束。

0≤Pei,t≤Pmax

(5)

(6)

式中：Pmax为电动汽车最大充电功率;Bc为电动汽车电池容量;Ti,a为电动汽车i的接入时间;Ti,d为电动汽车i的离开时间;ηc为电动汽车充电效率。式(5)表明任一时刻的充电功率不能超过最大充电功率。式(6)表明电动汽车离开时，电池电量需达到结束时期望充电状态。将约束(3)～(6)统一表示成：

Pei=[Pei,1,Pei,2,…,Pei,T]T⊆Fei

(7)

式中：Fei表示由约束(3)～(6)所决定的电动汽车i充电方案的可行域。

1.2.2配电网系统约束

配电网开环运行，呈树状结构，用DistFlow方程[10]来表示潮流较为方便。正常情况下，节点之间的电压降与节点电压相比较小，线路功率损失和线路所传输的功率相比也较小，因此不少研究对DistFlow方程进行了简化，忽略支路功率损失项，得到近似的支路潮流方程[11]。本文拟采用该方程来表示电动汽车接入下的配电网系统约束：

(8)

Pj+1,t=Pj,t-(Pdj,t+Paj,t)

(9)

(10)

(11)

(12)

U0,t=1

(13)

(14)

随着电动汽车保有量的不断上升，集中求解式(2)～(14)的速度、效率将会下降，甚至出现“维数灾”，对网络的承载能力和带宽也有比较高的要求。此外，由于集中控制需要电动汽车车主上传用户信息，会涉及用户隐私保护。因此，下文研究一种基于增广拉格朗日方法的聚合商分散充电控制策略。

2 聚合商分散充电控制策略

2.1 聚合商分散充电控制策略的实现机制

在电动汽车聚合商分散充电控制策略中，聚合商控制中心、各个节点网关以及个体电动汽车智能充电单元之间进行信息通讯与数据传递，从而实现电动汽车充电的有序控制。

图1为本文的分散充电控制策略实现机制示意图。由图1可知：聚合商控制中心自上而下将控制指令下达至节点网关，节点网关根据指令计算节点控制信号并进一步下发控制信号至节点下的电动汽车智能充电单元；电动汽车智能充电单元根据节点控制信号以及用户充电需求等计算充电方案，上传充电方案至节点网关，随后节点网关汇总节点下的充电总负荷，上传至聚合商控制中心，聚合商控制中心根据上传方案调整并更新下发至节点网关的指令。按照上述步骤循环直到收敛为止。智能充电单元可以对电动汽车的充电时间与功率大小进行控制。下文将对该分散充电控制策略的具体模型、传递信息的计算方式以及流程等进行详细阐述。

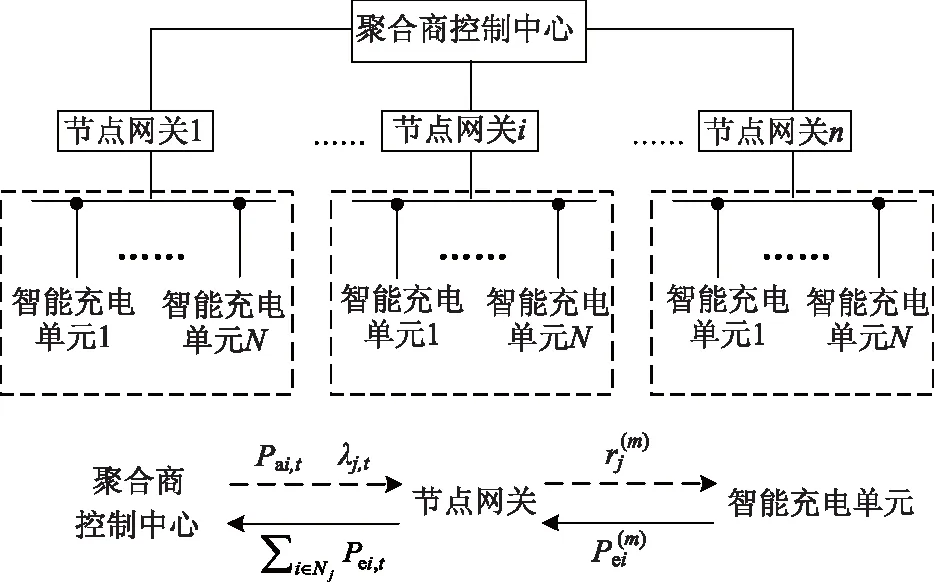
图1 分散充电控制策略实现机制示意图Fig.1 Implementation mechanism of the decentralized charging controlling strategy

2.2 分散充电控制模型建立

根据公式(2)～(14)建立分散充电控制模型为

(15)

约束条件(8)使得Pei,t与Paj,t之间存在耦合，因此对式(15)构造增广拉格朗日函数如下：

AL(∑i∈NjPei,t,Paj,t,λj,t)=

(16)

式中：ρ为二次惩罚项系数;λj,t为拉格朗日乘子。二次项缓解了拉格朗日松弛法的振荡现象，但带来不易分解项[11-13]，根据ADMM方法[12]，求解问题(15)可转化为交替迭代(17)～(19)：

(18)

(19)

上标k代表迭代次数。对以上各式进行说明：

(20)

聚合商控制中心汇总充电方案并判断系统约束是否越限，若不越限，则通过此方案，提前结束整个流程。

第二步：设ALj具有以下格式：

ALj(∑i∈NjPei,t,Paj,t,λj,t)=

式(18)等价于各个节点并行计算以下子问题：

(22)

式(22)中的目标函数依然存在二次项，同一节点j下的电动汽车之间存在耦合，本文运用文献[6]所提出的ODC方法对式(22)进行分散求解，求解实现方法如下：

① 设置最大迭代次数k、极小值ε。选择γj(0<γj<βNj)，节点下辖的电动汽车初始化充电方案(根据式(20))，并上传至所在节点。令m=1,m表示ODC迭代次数。

(23)

③ 电动汽车智能充电单元计算充电方案并上传至节点:

(24)

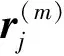
第三步：聚合商控制中心根据式(19)更新拉格朗日乘子。

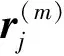
2.3 分散充电控制算法流程

通过ADMM和ODC相结合(称为ADMM-ODC法)，得到配电网下聚合商分散控制电动汽车充电的策略。图2为ADMM-ODC算法流程。

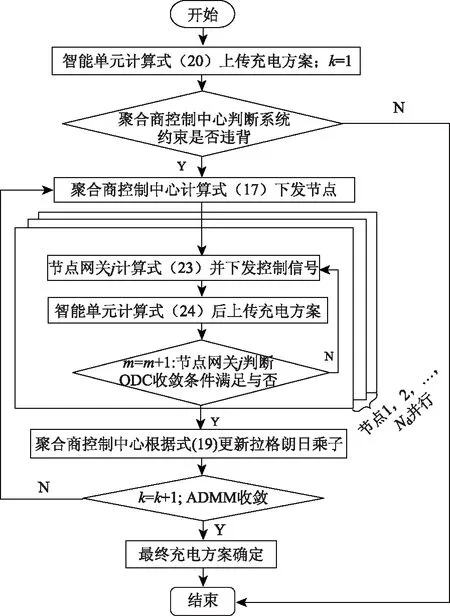
图2 ADMM-ODC算法流程图Fig.2 Flowchart of ADMM-ODC algorithm

3 仿真分析

3.1 仿真场景及参数设置

本文进行电动汽车充电控制策略研究，以图3所示的IEEE33节点系统做仿真分析。仿真所用的系统参数与文献[3]中一致。具体设置如下：

① 假定除节点0以外的其它节点均接入电动汽车，电动汽车总数量一定，每一个节点下接入电动汽车的数量按照各节点基础负荷比例设定。

② 电动汽车电池容量为32kWh，最大充电功率为7kW，充电效率为90%。

③ 电动汽车的接入时间、离开时间以及期望充电电量等数据根据2009年全美私家车出行统计结果通过蒙特卡洛抽样建模方法得到。

④ 聚合商收取的充电服务电价及购电分时电价等采用文献[4]中的设置,如表1所示。

⑤ 本文的结果均是在配有Intel双核2.4GHz CPU和2G内存的电脑上获得的，用Matlab调用CPLEX求解。

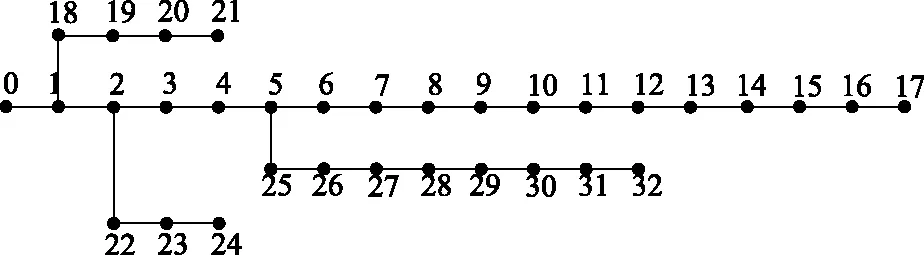
图3 IEEE 33节点图Fig.3 IEEE 33 bus system

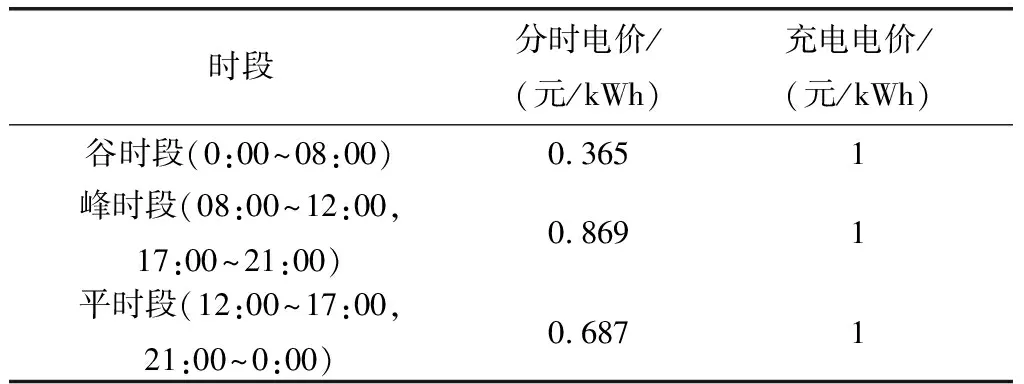
表1 电价参数设置Tab.1 Parameter setting of the electricity price

3.2 聚合商充电收益结果

表2对不同控制策略下的收益进行了比较，集中充电控制策略下的收益为全局最大收益。由表2可知，两种策略下的结果十分接近，ADMM-ODC算法能使聚合商的收益最大化。

3.3 电压平均相对误差

首先对电压平均相对误差指标作出说明。设运用ADMM-ODC算法所得出的各电动汽车的充电方案下节点j的实际电压幅值为

Uaj=[Uaj,1,Uaj,2,…,Uaj,T]T

(25)

根据式(9)～(13)所得出的节点j近似电压幅值为

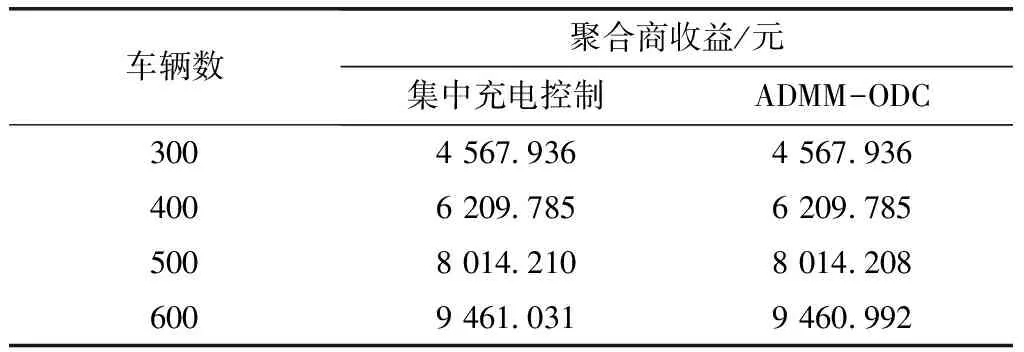
表2 不同控制策略下的聚合商收益比较Tab.2 Comparision of the aggregator′s revenue with different controlling strategies

Ulj=[Ulj,1,Ulj,2,…,Ulj,T]T

(26)

则节点j的电压平均相对误差为

(27)

图4为节点电压平均相对误差。由图可知，实际电压和近似电压之间存在一定误差，但误差程度较小。节点电压平均相对误差存在一定的规律，从支路顶端到支路末梢，节点电压平均相对误差逐渐增大(如节点0至节点17、18至21、22至24、25至32)，这是误差的叠加效应所造成的。为得到保证系统安全的方案，可更保守地选择约束的上/下限[11]。

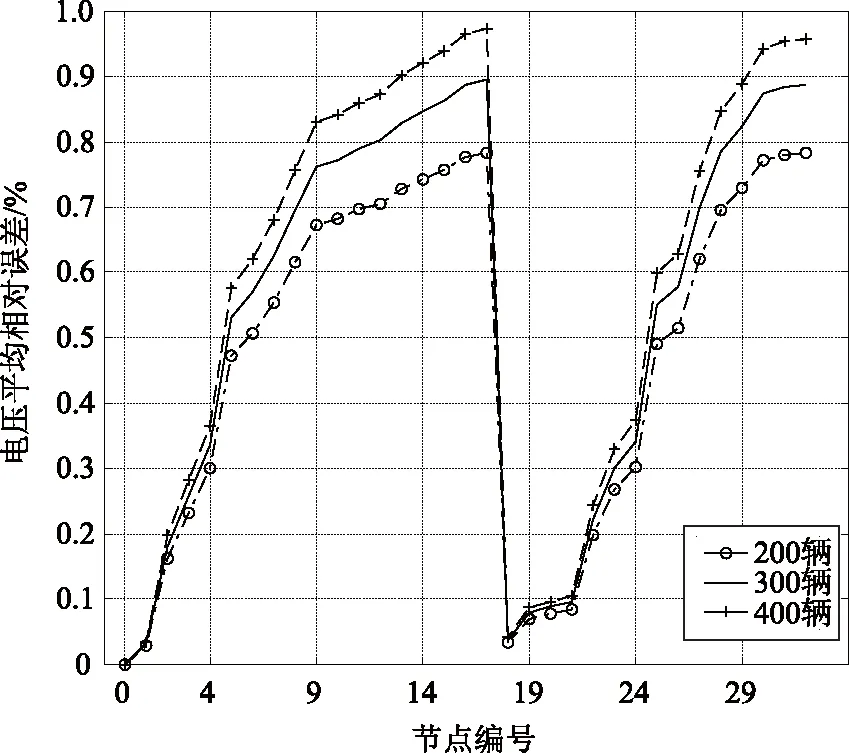
图4 电压平均相对误差Fig.4 Average relative errors of the voltage

3.4 ADMM-ODC算法收敛性

图5、图6分别给出了接入500辆电动汽车与接入600辆电动汽车时运用ADMM-ODC所得聚合商收益迭代图。当接入较多辆电动汽车时，按照式(20)上传的充电方案违背配电系统的约束，聚合商将通过控制信号实现电动汽车充电时段的调整，表现在收益迭代曲线上，会出现先下降后逐渐上升至最大收益并收敛的过程。

图5 电动汽车聚合商收益(接入500辆电动汽车)Fig.5 Revenue of the electric vehicle aggregator(plugged into 500 electric vehicles)

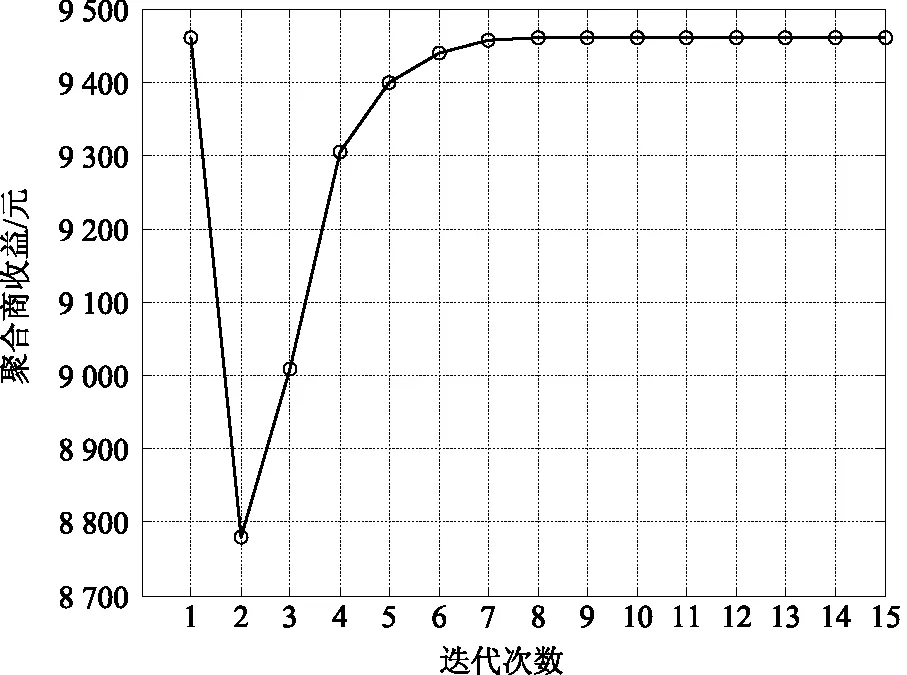
图6 电动汽车聚合商收益(接入600辆电动汽车)Fig.6 Revenue of the electric vehicle aggregator ( plugged into 600 electric vehicles)

作为对比，图7给出基于传统拉格朗日方法的分散充电控制策略下的收益迭代情况。由图可知迭代过程中出现了振荡，收益难以收敛。可见增广拉格朗日方法相比较于传统的拉格朗日方法具有优势，因为引入了二次项，提高了算法的收敛性能。

图7 电动汽车聚合商收益(接入500辆电动汽车，拉格朗日方法)Fig.7 Revenue of the electric vehicle aggregator (plugged into 500 electric vehicles, with lagrangian method)

3.5 计算效率

采用集中充电控制策略与采用ADMM-ODC算法的计算时间对比如表3所示(仿真过程中均忽略通信时间以及堵塞问题)。由表3可知，随着电动汽车数量的增多，集中充电控制的计算时间增长较快，计算效率降低，而ADMM-ODC算法由于将集中问题分解成子优化问题，可由每辆电动汽车并行计算，因此计算时间增长不明显，算法的计算效率较高。需要指出的是，接入400辆电动汽车时，ADMM-ODC算法的计算时间很短是因为由于按照式(20)计算并上传的充电方案直接被通过，提前结束了流程。

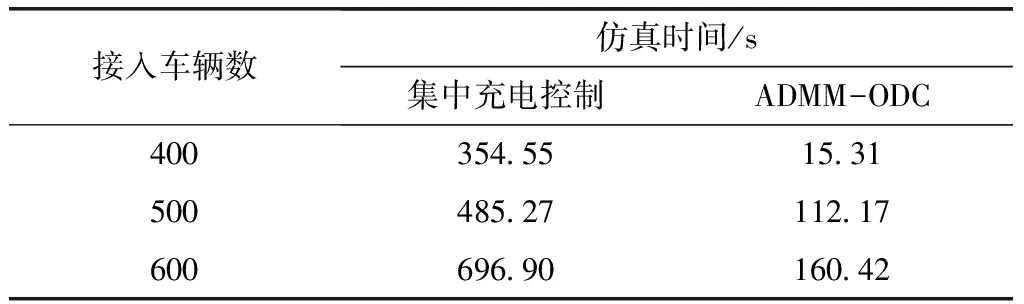
表3 不同控制策略下的计算时间比较Tab.3 Comparision of computing time with different controlling strategies

4 结束语

本文主要研究聚合商的分散充电控制策略。考虑配电网安全约束和电动汽车充电约束，并以分时电价机制下的收益最大化为目标，设计了电动汽车本地求解充电方案的分散充电控制策略。通过仿真分析可以得到如下结论：

① 在充电收益方面，采用本文所提出的分散充电控制策略与采用集中控制策略所得出的结果一致，均可实现聚合商收益最大化；

② 相比较于基于拉格朗日方法的分散充电控制策略，基于增广拉格朗日方法的分散充电控制策略收敛性较好；

③ 分散算法中由各个电动汽车计算本地充电方案，该过程是并行进行的，计算效率相比较于集中充电控制优势明显。

需要指出的是，本文中所设想的聚合商运营模式还较为简单，结合更为复杂的充电场景将是进一步深入研究的方向。