基于改进型天棚阻尼控制算法的馈能式半主动油气悬架系统
周创辉, 文桂林
(湖南大学 汽车车身先进设计制造国家重点实验室,长沙 410082)
馈能悬架中用一套能量回收装置替代传统的减振器,能够回收车辆行驶过程中由路面激励引起的悬架振动能量[1-2]。目前,研究和开发馈能式悬架系统已成为车辆工程领域的研究热点之一[3]。为了提高馈能悬架的工作性能,国内外学者对馈能悬架的半主动控制和主动控制进行了大量研究:Wang等[4]提出了一种采用直线电机作动器的馈能式主动悬架,通过控制电路来调节悬架的输出力,但控制算法比较复杂,且精度要求较高。欧阳冬等[5]提出了一种采用直流电机作动器的馈能式主动悬架,并对LQG控制算法下悬架的性能进行了仿真分析。Zhang等[6]基于直线电机馈能式主动悬架设计了一种H∞鲁棒控制器,实现悬架系统在主动减振和能量回收两种模式之间进行切换。寇发荣等[7-8]提出了一种利用航空用的电动静液压作动器技术的馈能式半主动悬架,可根据悬架的工作状态对能量管理模式进行切换,在最优控制算法下通过调节负载电阻改变馈能电流来实现阻尼力调节。汪若尘等[9]以LQG算法为参考,分析了直线电机馈能式悬架的半主动控制特性。Huang等[10]以滚珠丝杠-直流电机式馈能悬架为对象,设计了具有耗能全主动控制和馈能半主动控制两种模式的半主动控制器。林晨[11]以滚珠丝杠和无刷直流电机构成的馈能式悬架为对象,研究了最优控制算法、模糊控制算法和变论域模糊控制算法对悬架的半主动控制效果。从现有的研究结果来看,馈能式主动悬架能够通过模式切换协调车身平顺性和悬架的馈能,但对作动器和控制电路的要求较高,算法比较复杂。相比主动控制,半主动控制下的悬架系统结构和控制算法比较简单,对元件要求较低,成本也低。但是,现有的馈能式半主动悬架主要以车身平顺性为目标,忽略了悬架的馈能特性。此外,大多数半主动馈能悬架通过调节馈能电路的负载电阻来调节阻尼力。负载电阻将电能转化为热能,不利于馈能悬架回收能量的再利用。
天棚阻尼控制由于算法简单,实用性高,在半主动悬架中得到了广泛应用[12]。但是,传统的天棚阻尼半主动控制算法以改善汽车的平顺性为目的,没有考虑对悬架的馈能特性的影响。本文针对液-电馈能式油气悬架系统,提出一种改进型的天棚阻尼半主动控制算法,通过调节液压马达排量实现悬架系统的半主动控制。该算法以车体和车轮的速度以及发电机的转速为判断依据,综合考虑了馈能悬架的减振和馈能特性。在1/4车辆模型中,将该算法与传统天棚阻尼半主动控制和被动控制分别用于馈能式油气悬架系统进行仿真对比,分析该算法对车辆的乘坐舒适性和操纵稳定性,以及对悬架的馈能特性的影响
1 液-电馈能式半主动油气悬架系统
图1所示为一种可用于大中型SUV车辆上的液-电馈能式半主动油气悬架系统。该系统通过两个单向阀组成液压整流回路,将悬架的线性往复运动转换为液压马达的单向旋转运动,再由液压马达带动旋转式发电机将悬架振动能量转化成电能。其中,液压缸作为承载部件,支撑在车体和车桥之间。活塞杆与缸体分别通过销轴安装在车体和车桥上。液压缸的活塞上设计油孔,将上下两个工作腔导通,使其等同于一个柱塞缸。活塞和缸筒之间不需要密封圈,只需要导向环。因此,液压缸的缸内摩察力和泄漏可以忽略。此外,活塞上的油孔设计为多个直径较大的通孔,总通流截面积较大,压力损失可以忽略。发电机采用汽车用发电机,带整流和稳压器,输出14V直流电压向蓄电池充电。液压马达的排量可以通过控制单元输出电信号进行调节。
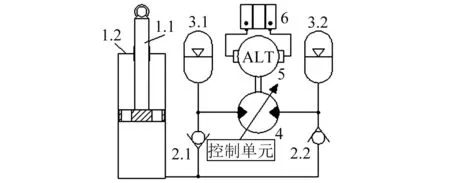
1.1—活塞杆; 1.2—缸筒; 2.1—单向阀(正向安装);2.2—单向阀(反向安装); 3.1—高压侧蓄能器; 3.2—低压侧蓄能器; 4—变量液压马达; 5—发电机; 6—蓄电池图1 馈能式半主动悬架结构图Fig.1 Layout of regenerative and semi-active suspension
在路面激励作用下,车体和车轮之间产生相对运动,引起悬架往复振动,即活塞杆相对缸体往复运动。当悬架被压缩时,活塞杆被压进缸筒内,导致缸内油液压力升高。液压缸的压力高于两个蓄能器的压力,单向阀2.1打开,而单向阀2.2关闭。从液压缸流出的高压油经过单向阀2.1后,一部分进入蓄能器3.1,使蓄能器3.1的压力高于蓄能器3.2的压力。同时,另一部分高压油通过液压马达进入蓄能器3.2。当悬架被拉伸时,活塞杆从缸筒内拔出,导致缸内油液压力降低。液压缸的压力低于两个蓄能器的压力,单向阀2.1关闭,而单向阀2.2打开。蓄能器3.2内的油液经过单向阀2.2补充到液压缸中,使蓄能器3.2的压力低于蓄能器3.1的压力。同时,蓄能器3.1中的部分高压油通过液压马达和单向阀2.2也补充到液压缸中。在悬架的两个工作行程中,液压油始终从蓄能器3.1的流向蓄能器3.2的方向,保证了液压马达和发电机单向旋转。
在悬架系统中,每个元件参数对系统的工作性能都有一定影响。机械部分的摩擦力和液压管路中的流体阻尼力,是不可控的,且在悬架的输出力中占比很小。实际工程中,液压缸和蓄能器的参数在装机后在是不能实时调节的,但变量液压马达的排量可以通过电信号调节。在图1所示的系统中,液压马达通过刚性轴直接驱动发电机,两者的转速和扭矩相等。液压马达输出轴上的负载扭矩对液压系统的压力有直接影响。发电机的转速对其输出电流、功率和输入扭矩有直接影响。当流量一定时,液压马达的转速和排量成反比。在路面激励下,进出液压缸的流量是确定的。此时,调节液压马达的排量可以改变发电机的转速,进而调节发电机的输出电流和功率。另一方面,输出电流的变化会直接引起发电机输入轴上的扭矩变化,即液压马达输出轴上负载扭矩的变化。液压马达两端的压力差由输出轴上负载扭矩决定。因此,通过调节液压马达排量改变发电机输出电流可以影响液压系统的压力,从而对悬架系统的输出力进行控制。
2 数学模型
结合馈能式油气悬架系统的工作原理,可以得到压缩和伸张两个行程中的流量和压力关系。图2所示是液压系统中流量和压力的分布示意图。
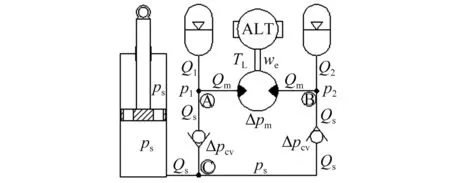
图2 液压系统中流量和压力分布示意图Fig.2 Flow and pressures in the hydraulic system
压缩行程中,油液从液压缸流出后沿结点C→A→B流动,系统中的流量压力关系满足:
(1)
伸张行程中,油液从蓄能器3.1流出后沿结点A→B→C流动,系统中的流量压力关系满足:
(2)
式中:ps和Qs分别为液压缸的油液压力和进出流量;p1和p2分别为蓄能器1和蓄能器2的压力;Δpcv1和Δpcv2分别为单向阀1和单向阀2上的压力损失;Qac1和Qac2分别为进出蓄能器1和蓄能器2的流量;Δpm和Qm分别为液压马达上的压力差和流量。
液压缸活塞杆上的输出力等于悬架系统的输出力。根据图1中所示的结构,馈能悬架的输出力Fs可以表示为:
Fs=Asps
(3)
液压缸的进出流量Qs可以表示为:
(4)
式中:As为活塞杆截面积;Vs为液压缸工作腔等效体积;βe为油液的弹性体积模量;xb和xw分别为车身和车轮的位移。
图1中的两个单向阀规格和参数相同,其流量-压力关系可以表示为:
(5)
式中:Cd为单向阀的流量系数;Acv为单向阀的节流面积;ρ为油液的密度。
不考虑进口特性,两个蓄能器的压力和体积变化关系可以表示为:
(6)
式中:p0,ac和pt,ac为蓄能器工作前后的压力;V0,ac和Vt,ac为蓄能器初始体积;Qac为进出蓄能器的油液流量;λ为气体状态参数,λ=1.4。
根据液压马达的结构参数和工作原理,流经液压马达的流量Qm和液压马达上的压力差Δpm可以表示为:
(7)
式中:ωm为液压马达的转速;ηv为液压马达的容积效率;qm为液压马达的排量;ηm为液压马达的机械效率;Jm为液压马达及负载的等效转动惯量;Bm为液压马达阻尼系数;TL为液压马达输出轴上的负载扭矩。
发电机作为液压马达输出轴上的负载机构,需要的输入轴扭矩即为液压马达输出轴上的负载扭矩。在式(7)中,Jm已经包含了发电机的等效转动惯量。因此,作用在液压马达输出轴上的负载力矩可以表示为:
TL=Te=ktI
(8)
式中:kt为发电机的扭矩常数;I为发电机的输出电流。
根据汽车发电机原理,恒压整流后,发电机的输出的直流电压Ue可以表示为:
Ue=2.33keωe-IRe
(9)
式中:Ke为发电机的结构常数;Re为发电机的等效电阻。
不考虑电容特性,蓄电池充电时的伏安特性可以表示为:
(10)
式中:Uoc为蓄电池的电压;Rbat为蓄电池的电阻。
发电机的输出电能即为馈能悬架回收的振动能量。馈能悬架的馈能功率Pout可以表示为:
Pout=UeI
(11)
3 控制算法设计
3.1 传统天棚阻尼控制算法
天棚阻尼的理想模型是在车体和假想的天棚之间安装一个用于耗能的阻尼器。当阻尼系数达到一定值时,该方法能够获得相应的车体减振效果。但在实际车辆中,不存在假设的天棚,无法实现理想的控制力。因此,在应用天棚阻尼控制策略时,一般通过车体和车轮之间的可控执行元件来模拟天棚阻尼控制力。天棚阻尼控制是通过一个双态阻尼实现的‘on-off’开关式控制模式,其控制算法可以表示为[13]:
(12)
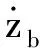
3.2 考虑馈能特性的改进型天棚阻尼控制算法
去掉图1中的控制单元,将液压马达设为定量液压马达,即为被动控制的馈能悬架系统。在AMESim中建立被动控制下馈能悬架的1/4车辆仿真模型,并根据系统数学模型选择各元件子模型,如图3所示[14-15]。
以某SUV车辆为对象,设计仿真模型中相应的悬架系统参数。车辆及悬架液压系统的参数设置表1所示。发电回路中采用汽车用发电机和蓄电池,参数如表2所示。
在被动控制下的1/4车辆模型中,分别以30 km/h、50 km/h和70 km/h车速下的一段C级路面为输入信号,液压马达排量在4~10 ml/r的区间内每隔0.5 ml/r取一次值进行仿真。依次对每组仿真得到车身加速度和发电机馈能功率的时域响应结果进行统计计算。图4和图5所示是不同液压马达排量时的车身加速度均方根值(RMS)和馈能功率的平均值。
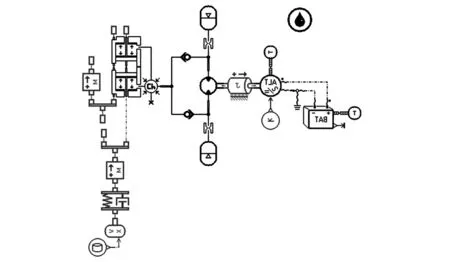
图3 馈能式被动悬架的1/4车辆仿真模型Fig.3 Quarter car simulation model for the regenerative suspension
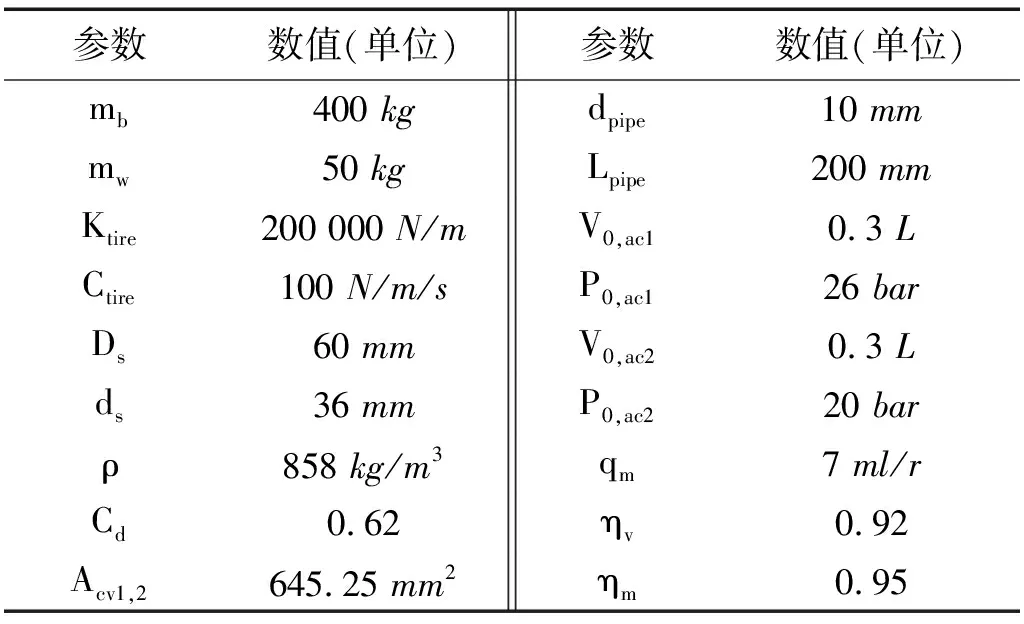
参数数值(单位)参数数值(单位)mb400 kgdpipe10 mmmw50 kgLpipe200 mmKtire200 000 N/mV0,ac10.3 LCtire100 N/m/sP0,ac126 barDs60 mmV0,ac20.3 Lds36 mmP0,ac220 barρ858 kg/m3qm7 ml/rCd0.62ηv0.92Acv1,2645.25 mm2ηm0.95
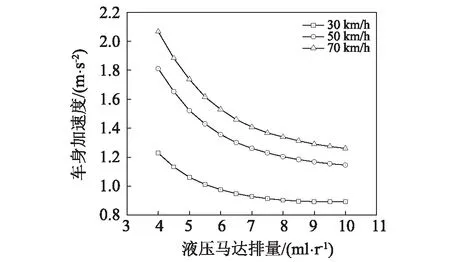
图4 不同液压马达排量对应的车身加速度均方根值Fig.4 RMS of car-body vertical accelerations for different hydraulic motor displacements

图5 不同液压马达排量对应的平均馈能功率Fig.5 Average electrical powers for different hydraulic motor displacements
对比图4和图5可知,馈能悬架在隔振和馈能两个方面是互相对立的。减小液压马达排量有助于提高馈能功率,但车身加速度的均方根值也随之增大,车辆的舒适性变差。反之,加大液压马达的排量能够改善车辆舒适性,但馈能效果会变差。实际上,汽车发电机正常工作时有最低转速要求。低于最低转速时,汽车发电机没有电流输出。在这种情况下,减小液压马达排量能够增大发电机的转速,有助于提高馈能效果。依据上述分析,设计兼顾减振和馈能的改进型天棚阻尼半主动控制规则,如表3所示。
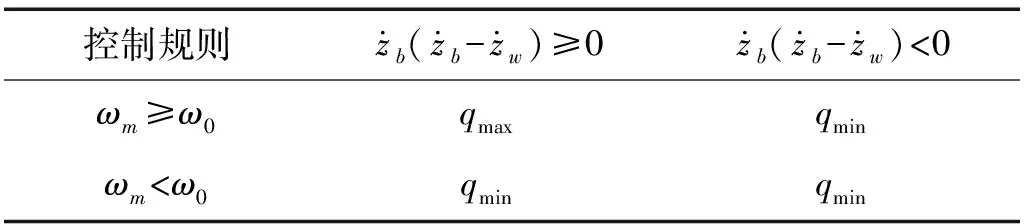
表3 改进型天棚阻尼控制规则
表3中,ω0是使汽车发电机输出电流的最小转速。考虑到响应滞后,ω0的取值比汽车发电机的最小工作转速稍大一些。综上所述,考虑馈能特性后的天棚阻尼半主动控制数学表达式为:
(13)
4 仿真分析
根据悬架系统的数学模型和控制策略,联合MATLAB和AMEsim建立馈能式半主动油气悬架1/4车辆仿真模型,并根据系统数学模型选择适当的元件子模型,如图6所示[16]。该模型中,液压马达的最小排量qmin设为6 ml/r,最大排量设为8 ml/r,发电机的参考转速ω0设为1 100 r/min,其他参数和图3所示的仿真模模型参数相同。
4.1 时域分析
(1)正弦激励
正弦激励是研究车辆垂向振动的常用激励方式。车身加速度对车身共振频率附近的激励信号更敏感,而汽车的车身共振频率一般比较低。因此,以正弦信号(频率为1.5 Hz,幅值为0.04 m)为输入,分别对被动控制、天棚阻尼半主动控制和改进型天棚阻尼半主动控制三种算法对应的车身加速度、悬架动挠度、车轮动载荷和能量回收功率的响应进行对比。仿真时间设为10 s,结果如图7所示。
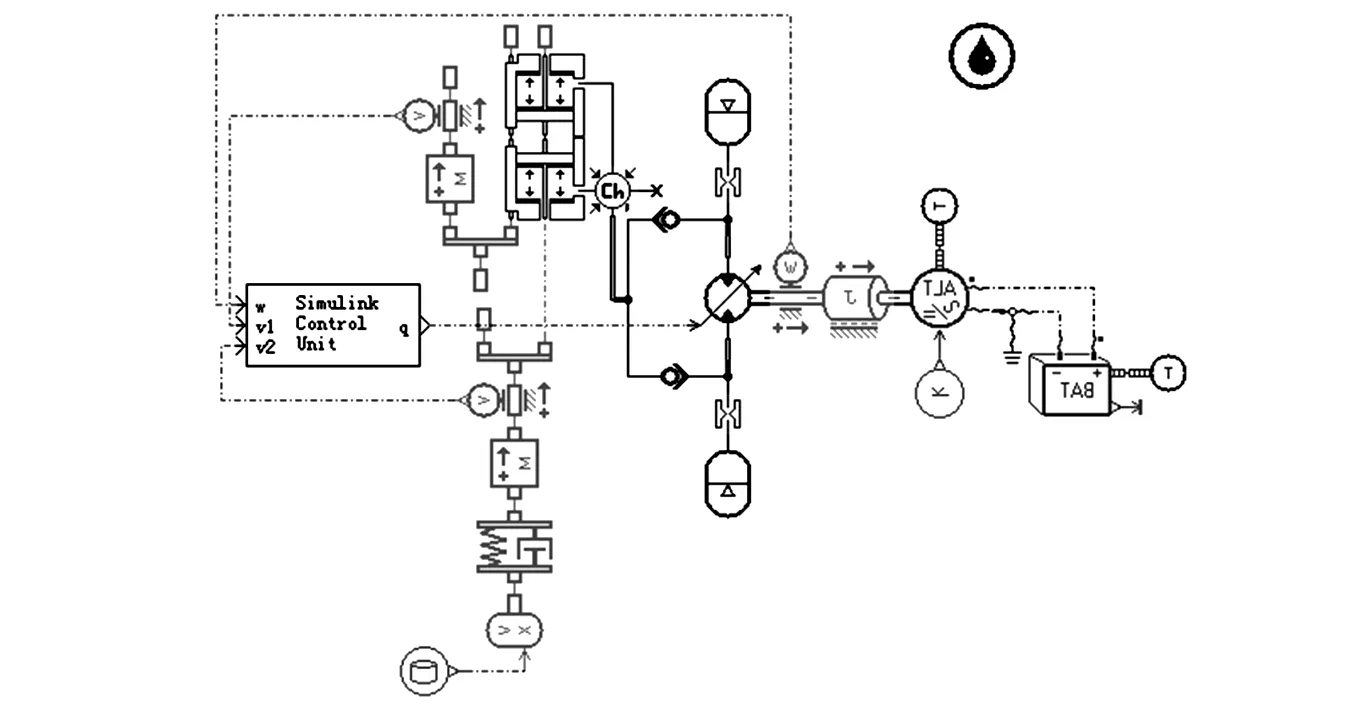
图6 馈能式半主动悬架的1/4车辆仿真模型Fig.6 Quarter car simulation model for the regenerative and semi-active suspension
从图7中可知,两种天棚阻尼半主动控制算法下车身加速度、车轮动载荷和悬架的馈能功率比被动悬架都明显减小。这说明两种天棚阻尼控制算法在低频正弦激励下能够有效改善车辆的乘坐舒适性和操控稳定性,但降低了悬架的馈能效果。和传统天棚阻尼控制算法相比,改进型天棚阻尼控制算法对应的车身加速度和车轮动载荷有小幅度的增大,但馈能功率明显增大。这说明改进型天棚阻尼半主动控制算法在改善车辆平顺性的同时也能保证较好的馈能效果。
(2)随机路面激励
研究车辆在随机路面激励下的响应,对车辆的的行驶平顺性和操纵稳定性等有更实际的意义。不平路面的激励是汽车行驶时的主要激励,通常用数值模拟来替代。用积分白噪声法模拟一段50 km/h车速下的C级路面不平度作为输入信号,对图6所示的1/4车辆模型进行仿真。分别对采用被动控制、天棚阻尼半主动控制和改进型天棚阻尼半主动控制三种算法后的车身加速度、悬架动挠度、车轮动载荷和能量回收功率的响应进行对比。仿真时间设为为20 s,结果如图8所示。
由图8(a)可知,与被动控制相比,采用半主动控制得到的车身加速度更小,车辆舒适性得到明显改善;与传统天棚阻尼控制算法相比,改进型天棚阻尼控制算法得到的车身加速度更大,减振效果略差。由图8(b)和图8(c)可知,与被动控制相比,采用半主动控制得到的悬架动挠度和车轮动载荷略大。由图8(d)可知,与被动控制相比,采用半主动控制得到的回收功率更小,馈能效果变差;相比传统天棚阻尼控制算法,改进型天棚阻尼控制算法得到的回收功率更大,馈能效果得到明显改善。上述结果说明,考虑馈能特性后的改进型天棚阻尼控制算法不仅改善了车辆的行驶平顺性,还保证了悬架系统有较好的馈能效果。
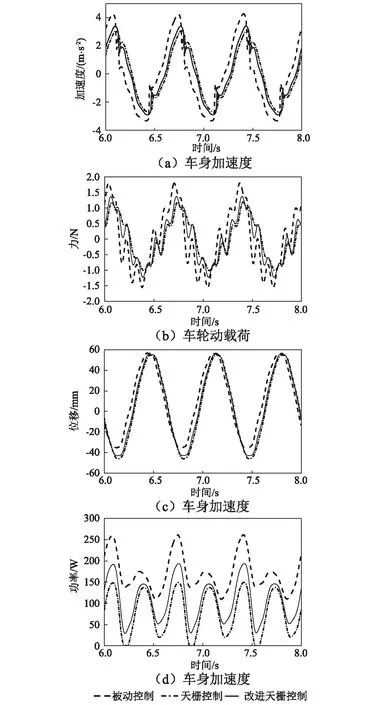
图7 正弦激励的时域响应Fig.7 Time-domain responses for a sinusoidal excitation
为了更直观对比三种控制方式下馈能悬架的性能,对时域响应结果进行计算。表4所示是三种不同控制方式对应的车体加速度、悬架动挠度、车轮动载荷的均方根值和峰值,以及悬架系统回收功率的平均值的计算结果。对比表中数据可以看出,改进型天棚阻尼半主动控制对应的各指标介于被动控制和传统天棚阻尼半主动控制之间。这说明,改进型天棚阻尼半主动控制相比被动控制有效改善了车辆平顺性,而相比传统天棚阻尼半主动控制则有效地改善了馈能效果和车辆的操控稳定性。
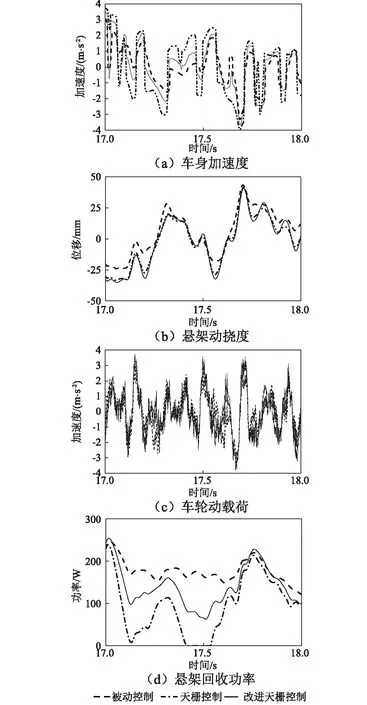
图8 随机激励的时域响应Fig.8 Time-domain responses for a random excitation

控 制方 式被 动控 制天棚阻尼控制传统改进型车身加速度/(m·s-2)均方根值1.721.381.47峰值4.824.614.70悬架动挠度/mm均方根值19.220.320.1峰值38.541.240.6车轮动载荷/N均方根值1 356.81 424.41 381.2峰值4 882.64 995.34 921.4平均回收功率/W110.492.3101.2
4.2 幅频特性分析
由弹簧和减振器构成的传统悬架系统可以看做是时不变的线性系统,其幅频特性一般可以通过传递函数得到。本文提出的馈能式半主动悬架系统具有较强的非线性,半主动控制后非线性更强烈,其频率特性不能直接通过公式表达。实际上,随机激励信号可以看做是由N个单频率信号的叠加,系统的频率特性也可以通过每个频率下的响应来表达。强非线性系统的幅频特性可以通过时域响应方差来近似计算,具体方法如式(14)[17-18]。
(14)
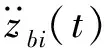
悬架的幅频特性一般主要考察车身共振频率和车轮共振频率附近的传递特性,以及车身共振频率与车轮共振频率之间的中频段的传递特性。因此,在0.6~13 Hz的范围内取25个点作为单频率激振信号的输入频率(即N=25)。在上述的1/4车辆仿真模型中,保持其他参数不变,运行仿真模型得到不同频率的正弦激励信号对应的时域响应。通过式(14)计算可得到车身加速度、悬架动挠度、车轮动载荷和能量回收功率相对位移激励的幅频特性,结果如图9所示。从图9(a)和图9(d)中可以看出,车身加速度和悬架回收功率的幅频特性比较接近。在低频段,改进型天棚阻尼半主动控制下的车身加速度传递率和传统天棚阻尼半主动控制接近,大于被动控制;而在中高频段,改进型天棚阻尼半主动控制下的车身加速度传递率在被动控制和传统天棚阻尼控制之间。从图9(b)中可以看出,改进型天棚阻尼半主动控制下的悬架动挠度传递率和传统天棚阻尼半主动接近,大于被动控制。从图9(c)中可以看出,改进型天棚阻尼半主动控制下的车轮动载荷传递率在被动控制和传统天棚阻尼控制之间。上述结果说明,考虑馈能特性的改进型天棚阻尼半主动控制算法兼顾了车辆行驶平顺性和悬架的馈能特性,符合设计要求。
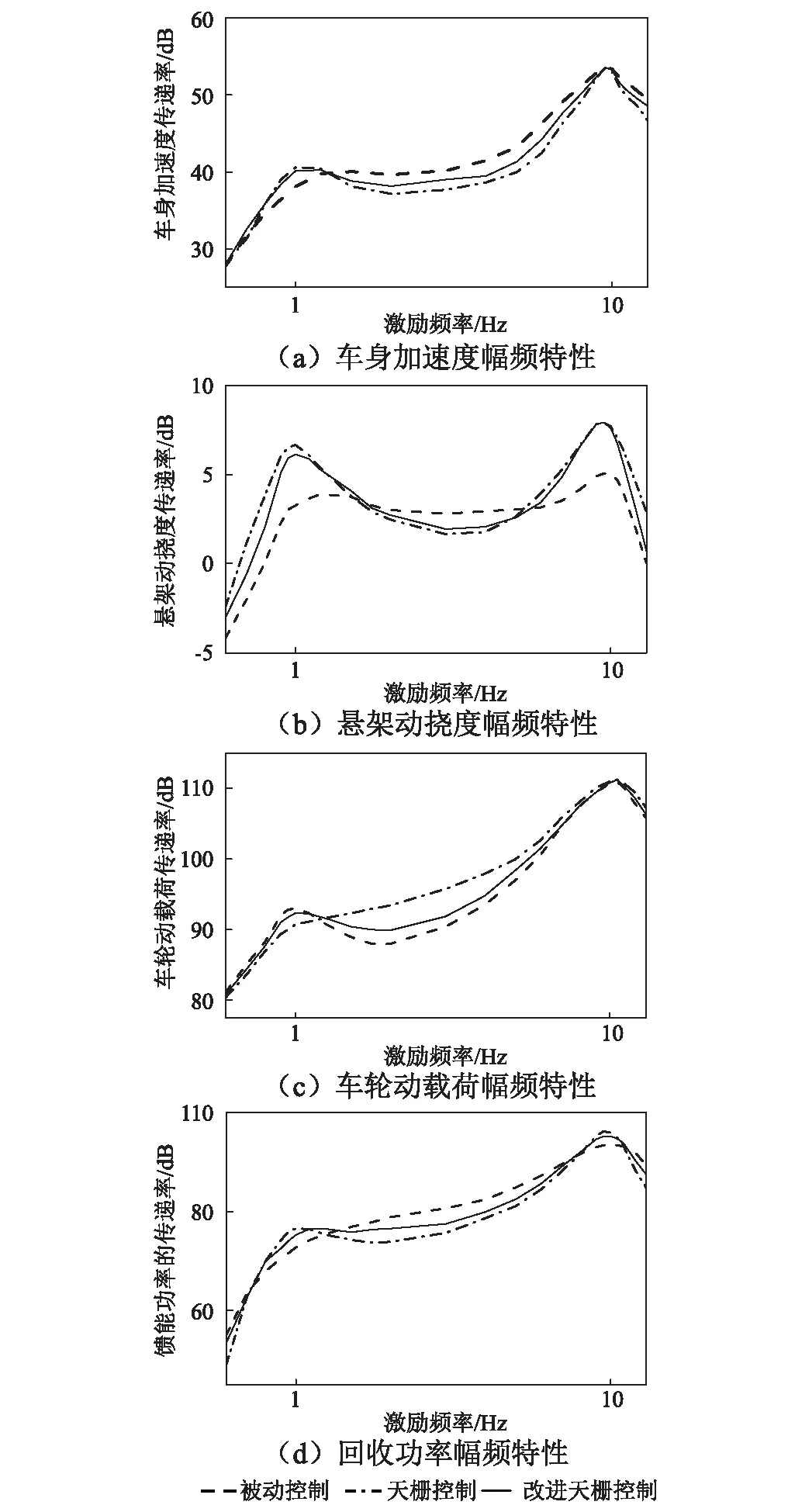
图9 幅频特性曲线Fig.9 Amplitude-frequency characteristic curves
5 结 论
针对液压-电馈能式油气悬架系统,提出一种兼顾减振和馈能特性的天棚阻尼半主动控制算法。该算法基于悬架速度和发电机转速的负反馈,通过控制液压马达排量变化实现悬架输出力的调节,进而改善悬架的性能。
在1/4车辆模型中,以正弦信号和随机路面信号为激励,分别对被动控制、传统天棚阻尼半主动控制和改进型天棚阻尼半主动控制算法下馈能悬架系统进行了仿真对比。结果表明,相比被动控制,两种天棚阻尼半主动控制算法都能够有效改善车辆的行驶平顺性。相比传统天棚阻尼半主动控制算法,改进型天棚阻尼半主动控制算法对车辆平顺性和悬架馈能性能之间做了均衡考虑,适当地提了高馈能功率。另外,改进型天棚阻尼半主动控制下的悬架系统幅频特性也介于被动控制和传统天棚阻尼半主动控制之间,有较好的减振和馈能性能。

