芯体截面梯度变化的点阵夹层结构吸能特性研究
朱凌雪, 朱晓磊
(1. 金陵科技学院 数学系,南京 211169; 2. 南京工业大学 机械与动力工程学院,南京 211816)
与传统单层板结构相比,点阵夹层结构在外载荷作用下,点阵芯子的弯曲以及点阵芯子与面板之间的剪切作用,使得点阵夹层结构的吸能特性得到大幅度提高;而且较高的孔隙率使得点阵夹层结构重量更轻。因此,具有较高比吸能特性的点阵夹层结构是轻质抗爆一体化结构永恒的目标。
功能梯度材料是集结构和功能于一体的新型材料,首先是由Yamanouchi等[1-2]提出。近年来,功能梯度泡沫材料作为典型的功能梯度材料,已经被证实具有其优异的吸能特性[3-6]。Xia等[7]研究了空爆载荷作用下功能梯度泡沫夹芯板吸能特性,并与传统泡沫夹芯板进行了对比,结果表明,与传统泡沫夹芯板相比,功能梯度泡沫夹心板具有更强的吸能特性,且正向的梯度化可以提高功能梯度泡沫夹心板的吸能特性。与泡沫材料相比,点阵夹层结构具有更高的承载能力。学者们针对点阵夹层结构静态和动态力学行为做了大量的研究[8-17]。为了提高蜂窝、波纹板冲击吸能特性,卢天健[18-23]探索了在蜂窝、波纹板夹层结构空隙中填充PMI泡沫、陶瓷及铝泡沫等等材料,提高其抗爆性能。
Ullah等[24]基于金属材料韧性损伤模型建立了受面外压缩载荷作用的点阵芯子吸能特性预测模型,该模型可以较好地计算点阵夹层结构的失效模式,预测点阵结构的失效应变和失效位置。Xu等[25]提出了芯子性能沿着板长方向呈梯度变化的功能梯度点阵夹层结构(FGLS),如图1所示,并通过三点弯曲实验探讨了该结构力学性能及失效模式。结果表明,这种功能梯度点阵夹层结构的主要失效模式是面板皱曲。与传统点阵夹层结构相比,在相同承载力下,功能梯度化点阵夹层结构具有更轻的质量。功能梯度点阵夹层结构充分发挥了结构优势,可以大幅度提高结构效率。同样Yu等[26]探索了梯度方向蜂窝增强的点阵夹层结构的力学特性。
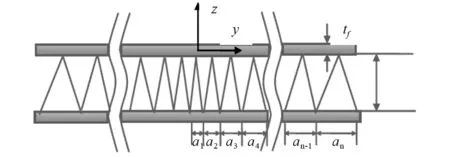
图1 功能梯度点阵夹层结构[12]Fig.1 Graded lattice core sandwich structure[12]
本文提出了一种芯杆直径沿点阵夹层结构厚度方向呈连续梯度变化的新型点阵夹层结构,用于提高点阵夹层结构抗爆吸能特性的新型点阵夹层结构。首先,根据弹性极限分析理论建立了芯体截面梯度变化的点阵夹层结构(LTSGCC)和传统点阵夹层结构(TLS)极限承载力计算模型;其次,在充分考虑材料塑性损伤及剪切损伤的前提下,应用有限元ABAQUS,探讨了芯体截面梯度变化的点阵夹层结构变形机理,并将其与传统结构变形机理进行了深入的对比;最后,探讨了梯度化系数对芯体截面梯度变化点阵夹层结构吸能特性的影响。
1 方法与模型
1.1 极限承载力预测模型
点阵夹层结构的能量耗散机制主要包括面板的弯曲与拉伸、芯子的压缩与剪切,其中芯杆的弯曲是点阵夹层结构主要的能量耗散方式[27]。当点阵夹层结构受到平压载荷的作用时,芯杆可以简化成两端固支受轴向载荷作用的压杆问题。当面外载荷小于临界屈曲载荷时,芯杆不发生弯曲变形,芯杆横截面应力小于屈服应力;当面外载荷等于临界屈曲载荷时,芯杆存在发生塑性弯曲的倾向,则芯杆横截面的应力等于屈服应力,此时,点阵夹层结构达到极限承载力;当面外载荷大于临界屈曲载荷时,芯杆在某一位置发生明显塑性弯曲变形,该截面应力等于屈服应力,则点阵夹层结构沿厚度方向变形量的增加其承载力逐渐降低。因此,点阵夹层结构极限承载力可以用于杆件发生弯曲变形的极限承载力来计算。
传统点阵夹层结构,其芯杆的直径处处相等,在外载荷的作用下,当芯杆开始发生塑性变形时,芯杆某处横截面应力达到材料屈服应力,则点阵夹层结构达到极限承载力,其计算如式(1)所示
Fcr=πσsD2sinθ
(1)
式中:D为芯杆直径,mm;σs为材料屈服应力,MPa;θ为芯杆与面板之间的夹角。对于芯体截面梯度变化的点阵夹层结构,如图2所示。从图2(b)可以看出,芯杆的直径从上面板至下面板呈连续变化。在外载荷的作用下,芯体截面梯度变化的点阵夹层结构芯杆某处横截面应力大于或等于塑性屈服应力时,芯杆存在发生塑性弯曲变形的倾向,则该结构达到了极限承载力,其计算式为
(2)
式中:lx为发生弯曲变形截面距离小端的杆长,mm;D1为大端直径,mm;D2为小端直径,mm。

图2 芯体截面梯度变化点阵夹层结构Fig.2 LTSGCC
1.2 有限元分析模型
应用ABAQUS/Explicit探讨两种点阵夹层结构吸能特性。其损伤主要是塑性损伤、剪切损伤、颈缩损伤以及这几种损伤的耦合。因此,本文应用Hoopeutra等[28]塑性损伤准则描述点阵夹层结构的塑性损伤;采用MSFLD(Müschenborn-Sonne Forming Limit Diagram)准则[29-32]描述点阵夹层结构的颈缩;采用Shear损伤起始准则描述点阵夹层结构的剪切损伤。且应变基的线性损伤扩展准则被用来计算点阵夹层结构损伤发生后的力学行为。
芯杆直径沿点阵夹层结构厚度方向呈梯度变化的点阵夹层结构,其面板和芯子采用铝合金,其材料牌号为EN AW-7108 T6,弹性模量为70 GPa,泊松比为0.33,屈服应力为311 MPa,拉伸强度为696 MPa。芯体截面梯度变化的点阵夹层结构与传统点阵夹层结构几何模型如图3所示,模型结构参数如表1所示;面板和芯子采用C3D8R,材料损伤本构模型参数如表2所示。在芯体截面梯度变化的点阵夹层结构平压实验计算的过程中,不考虑面板与芯子的界面脱粘,面板与芯子采用绑定约束;点阵芯杆之间采用自接触边界条件,摩擦因数取1.1;点阵芯杆与面板采用一般接触条件,摩擦因数取1.1[33]。
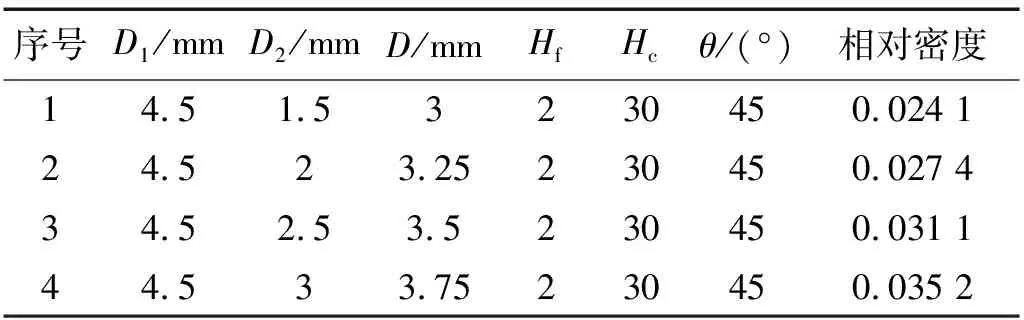
表1 模型结构参数

表2 损伤模型参数
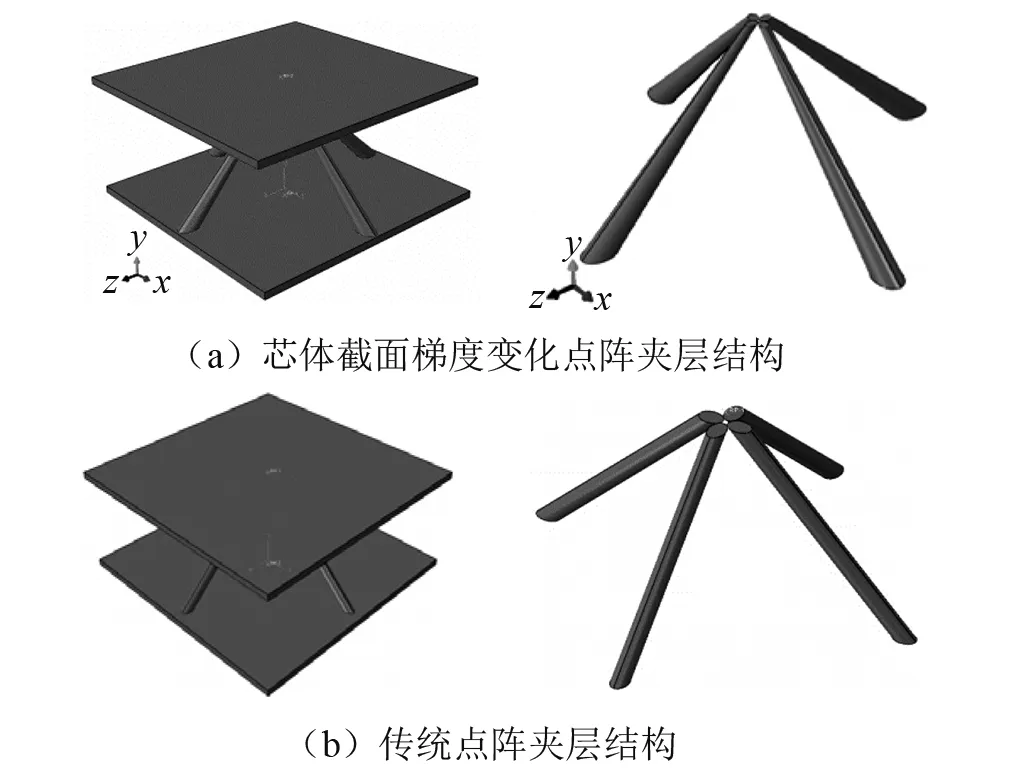
图3 几何模型Fig.3 The geometrical model
2 结果与讨论
2.1 变形特征
传统点阵夹层结构载荷位移曲线和Misses应力分布云图,如图4所示。变形特征如图5所示。从图4(a)可以看出,载荷位移曲线可以分成四个部分:第一部分为线弹性行为,点阵芯杆在压缩载荷的作用下达到屈服应力(如图4(b)所示),且芯杆未发生塑性变形(如图5(a)所示),点阵夹层结构达到极限承载,其数值为5 969.33 N;第二部分为芯杆的塑性弯曲变形,如图4(b)可以看出,传统点阵夹层结构发生塑性弯曲的位置是在芯杆的中间,即l/2处,这时点阵夹层结构的承载力随着位移的增加而逐渐降低。由图5(c)可知,当α=135°时,点阵夹层结构承载力达到最小值;第三部分为二次准弹性行为,结合图5(d)可知,当α<135°时,芯杆EF已经无法承受压缩载荷,而上、下面板与芯杆FG构成了新的点阵夹层结构,这个新构成的夹层结构具有一定的承载能力,使得点阵结构的承载呈近似线性的增加;第四部分为芯杆的二次弯曲变形行为,当载荷达到一定时,芯杆FG在芯杆EF的带动下,在H横截面达到塑性屈服应力,开始发生弯曲,且随着位移的逐渐增加芯杆FG在H界面的塑性弯曲转角逐渐增大,导致承载力逐渐下降。由图4(b)可以看出,在点阵芯杆发生塑性弯曲的整个过程中,弯曲截面上最大Misses应力均未超过EN AW-7108 T6的抗拉强度,说明点阵夹层结构在变形的过程中仅发生塑性变形而未发生破坏。
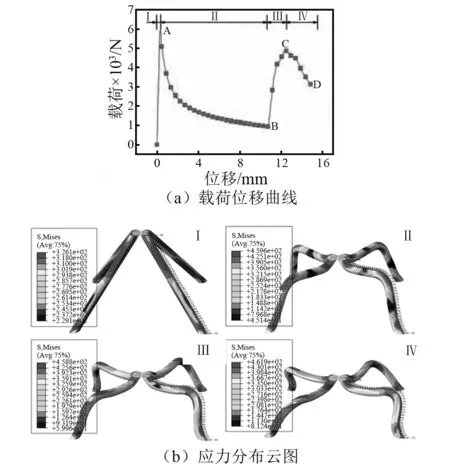
图4 传统点阵夹层结构载荷位移曲线及应力分布云图Fig.4 The TLS loading-displacement cure and Misses stress
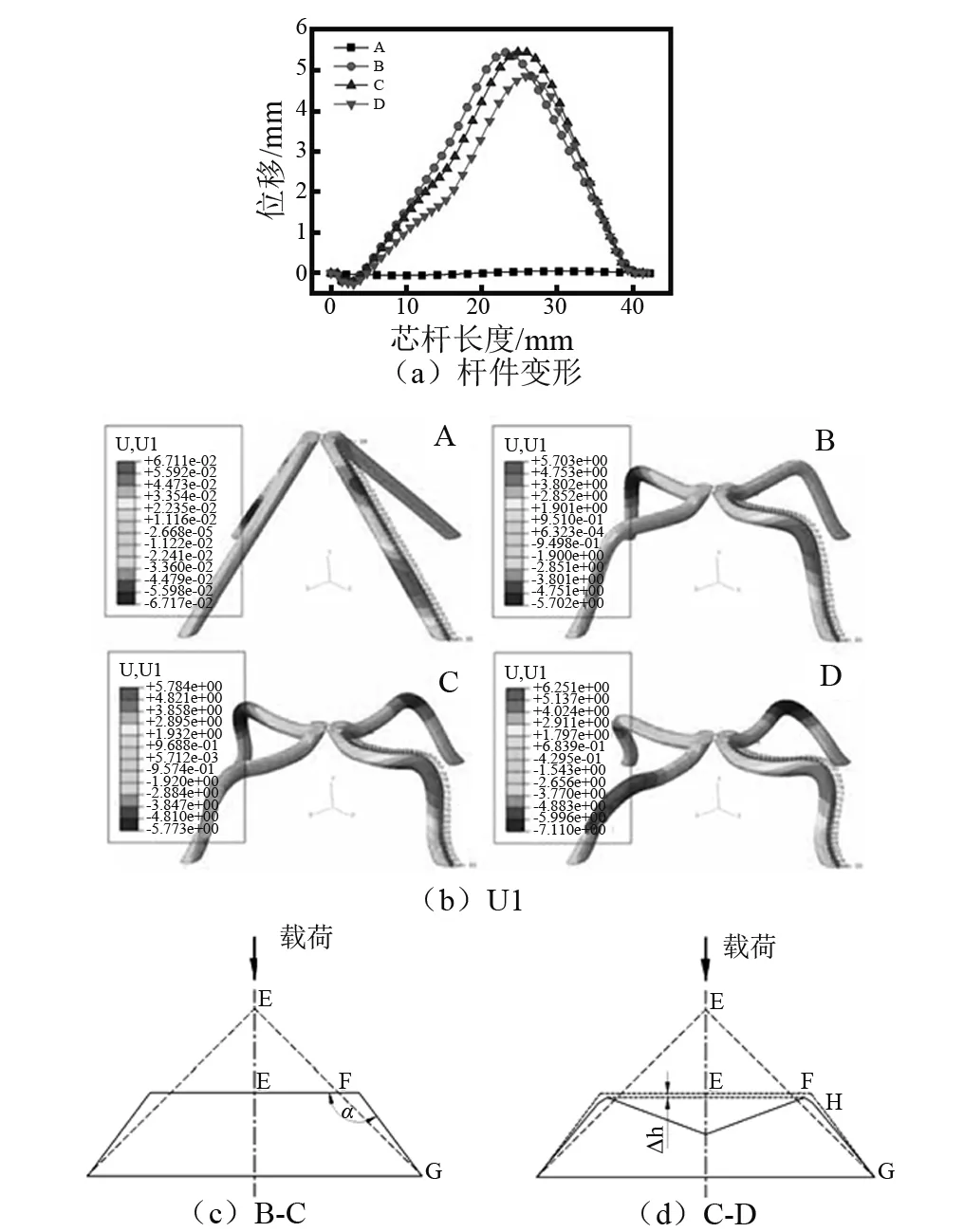
图5 传统点阵夹层结构变形特征Fig.5 TLS Deformation
芯体截面梯度变化的点阵夹层结构载荷位移曲线和Misses应力分布云图,如图6所示,其变形特征如图7所示。从图6(a)可以看出,芯体截面梯度变化的点阵夹层结构的载荷位移曲线同样可以分成四个部分:第一部分为线弹性行为,随着外载荷的增加点阵杆横截面应力迅速达到屈服极限(如图6(b)所示),且杆件未发生明显弯曲变形,如图7所示。与传统点阵夹层结构有所不同,此时芯体截面梯度变化的点阵夹层结构未达到极限承载力。第二部分为小端弯曲变形行为,由图7(a)可知,杆件发生弯曲的面为在l/8处,由于小端与面板绑定约束及杆件的相互拘束,使得杆件EF的弯曲变形受到限制,从而芯体截面梯度变化的点阵夹层结构承载力呈非线性增加;当α1=135°时,芯体截面梯度变化的点阵夹层结构达到极限载荷2 310.64 N。第三部分为杆件在l/4处的弯曲变形行为,芯体截面梯度变化的点阵夹层结构承载力随着变形的增加而逐渐降低;当α1=135°、α2=90°时,其承载力达到最小值。第四部分为二次准线弹性变形行为,结合图7(d)可知,当α1=135°、α2=90°时,上、下面板和杆件HG构成了新的芯体截面梯度变化的点阵夹层结构,使得结构承载呈非线性增加;当杆件HG发生塑性弯曲变形时,载荷稍微有所下降;随着位移的逐渐增加,杆件弯曲截面逐渐向下面板靠近,且弯曲截面面积逐渐增大,因此,芯体截面梯度变化的点阵夹层结构承载力稍微有些降低出现平台。由图6(b)可知,在芯体截面梯度变化的点阵夹层结构变形的过程中,芯杆横截面的应力均未超过EN AW-7108 T6的抗拉强度,说明芯体截面梯度变化的点阵夹层结构在变形的过程中仅发生塑性变形而未发生破坏。
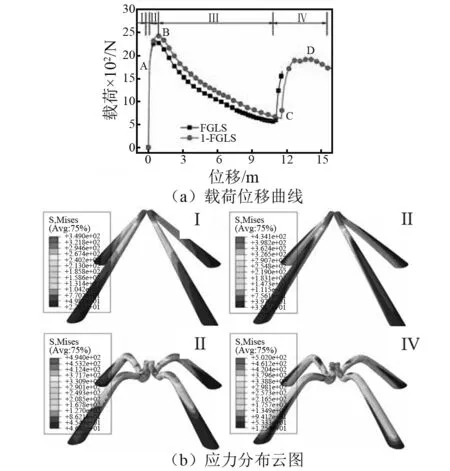
图6 芯体截面梯度变化点阵夹层结构载荷位移曲线和应力分布云图Fig.6 TheLTSGCC loading-displacement cure and Misses stress
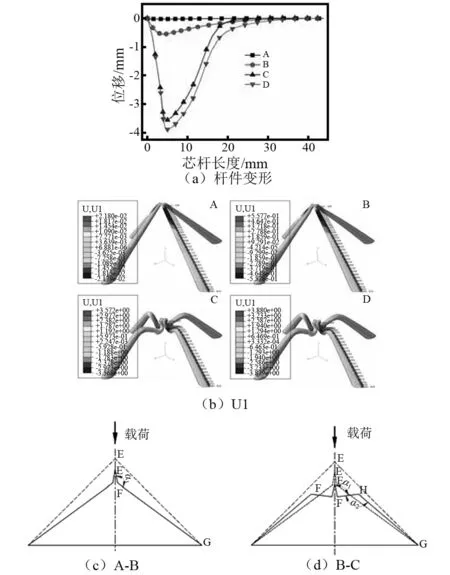
图7 芯体截面梯度变化点阵夹层结构变形示意图Fig.7 LTSGCC deformation
综上所述,与传统点阵夹层结构相比,芯体截面梯度变化的点阵夹层结构存在如下优势:①芯体截面梯度变化的点阵夹层结构的极限承载力要低于传统点阵夹层结构;②当α1<π/2和α2≈π/2+θ时,芯体截面梯度变化的点阵夹层结构承载力随着变形的增加呈阶梯状增大。
2.2 极限承载力分析
假设芯体截面梯度变化的点阵夹层结构梯度化系数λ=(D1-D2)/Hc。传统点阵夹层结构和芯体截面梯度变化的点阵夹层结构极限承载力分别用式(1)和式(2)计算,理论计算结果与有限元结果对比如图8所示。对于芯体截面梯度变化的点阵夹层结构来说,杆件l/8处界面发生塑性弯曲,且当α1=135°时,芯体截面梯度变化夹层结构达到极限承载力。
如图8所示,传统点阵夹层结构极限承载力理论计算结果与有限元分析结果之间最大误差为4.1%;芯体截面梯度变化的点阵夹层结构极限承载理论计算结果与有限元分析结果之间最大误差约为8.9%。这是因为随着小端直径的增加,芯体截面梯度变化的点阵夹层结构极限载荷所对应的发生弯曲的横截面的位置由l/8向着l/2处转移,而式(2)在计算芯体截面梯度变化点阵的夹层结构极限承载力时,是按照l/8处横截面面积计算的,因此,理论计算结果比有限元计算结果偏小,且随着梯度化系数的增大误差逐渐增大。相同等效密度条件下,芯体截面梯度变化的点阵夹层结构和传统点阵夹层结构极限承载力之比与梯度化系数之间的关系如图9所示。从图9可以看出,随着梯度化系数的增加芯体截面梯度变化的点阵夹层结构和传统点阵夹层结构极限承载力之比逐渐降低,即梯度化程度越高,芯体截面梯度变化的点阵夹层结构极限承载力越低。这是因为梯度化系数越高,芯杆小端直径越小,l/8处的面积越小,越易发生弯曲变形,导致极限承载力下降。传统点阵夹层结构属于前程吸能元件,在冲击载荷作用下,其吸能稳定性较差,且易发生破坏从而影响吸能。而芯体截面梯度变化的点阵夹层结构,载荷位移曲线相对较为平缓,大大改善了传统点阵夹层结构的前程吸能特性,提高了结构吸能的稳定性。
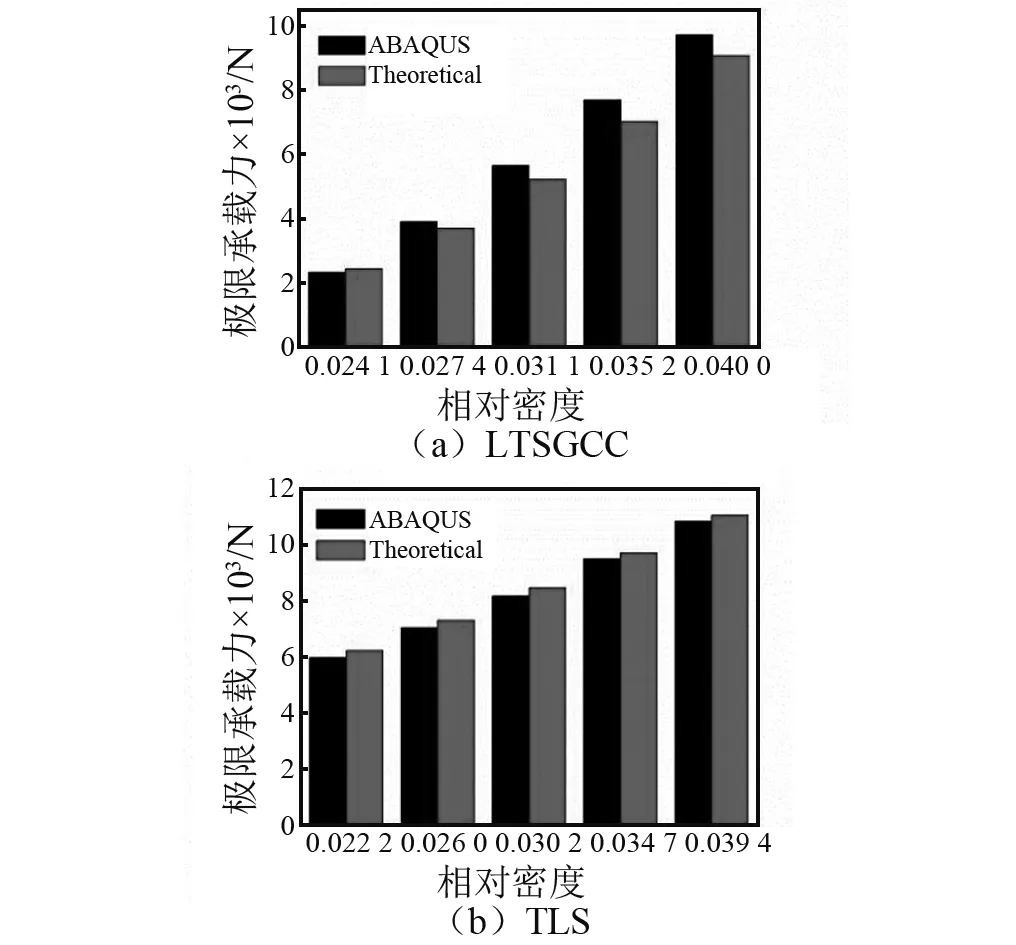
图8 极限载荷理论模型计算结果与有限元结果对比Fig.8 Results comparation between theoretical computation and ABAQUS
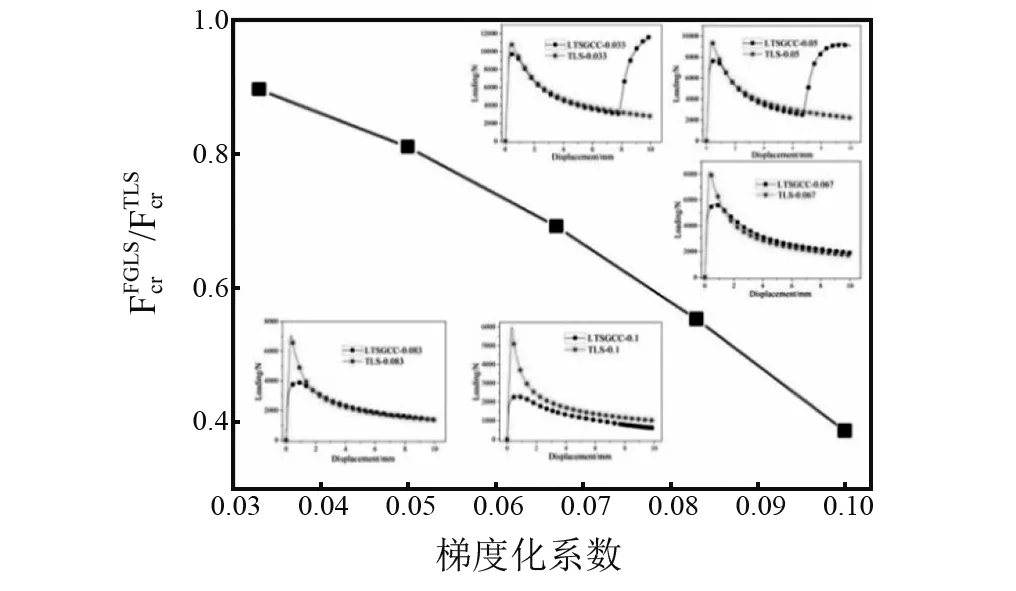
图9 极限承载力与梯度化系数之间的关系Fig.9 The relationship between first peak value ratio and gradient coefficient
2.3 吸能特性
对于抗空爆结构来说,吸能特性是评价结构性能的重要指标。目前,评价结构吸能的指标主要有:面比吸能(SEA),平均圧溃载荷(MCF)和圧溃载荷率(CLE),其计算公式如式(3)~(6)所示:
(3)
(4)
(5)
(6)
式中:EA为结构吸能,J;F为结构承载力,N;δ为压缩位移,mm;M为结构质量,kg; PCF为结构极限承载力,N。芯体截面梯度变化的点阵夹层结构面比吸能与梯度化系数之间的关系,如图10所示。
从图10可以看出,在相同的相对密度条件下,当梯度化系数小于0.07时,芯体截面梯度变化的点阵夹层结构面比吸能要大于传统点阵夹层结构。因此,适当的梯度化可以提高点阵夹层结构的吸能特性。这是因为芯杆的弯曲变形是点阵夹层结构吸能的重要途径,对于传统点阵夹层结构来说,芯杆发生塑性变形产生12个塑性铰,而芯体截面梯度变化的点阵夹层结构将产生16个塑性铰,即芯体截面梯度变化的点阵夹层结构的芯杆更容易发生塑性弯曲。而结构的吸能与塑性铰数量有着直接的关系,塑性铰越多则结构吸能特性越强,因此,芯体截面梯度变化的点阵夹层结构面比吸能要大于传统点阵夹层结构,当梯度化系数为0.05时,芯体截面梯度变化的点阵夹层结构面比吸能达到最大。
CLE是衡量结构吸能稳定性的重要指标,当CLE越接近于1说明结构的吸能稳定性越好。对于传统点阵夹层结构而言,由于结构极限承载力较大,没有吸能平台区,导致CLE较小,则结构吸能稳定性较差。芯杆梯度化可以有效地降低点阵夹层结构第一峰值承载力,从而提高结构的吸能稳定性。芯体截面梯度变化的点阵夹层结构压溃载荷率与梯度化系数之间关系如图11所示。从图11可以看出,芯体截面梯度变化的点阵夹层结构的压溃载荷率均高于传统点阵夹层结构,且当梯度化系数为0.05时,压溃载荷率达到最大值。
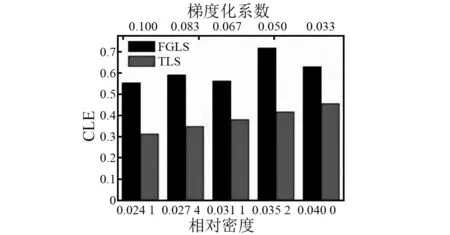
图11 芯体截面梯度变化点阵夹层结构与传统点阵夹层结构的压溃载荷率对比Fig.11 CLE comparation between LSGCC and TLS at different relative density
综上所述,芯杆截面梯度变化可以有效地提高点阵夹层结构的面比吸能,同时提高点阵夹层结构的吸能稳定性,且当梯度化系数为0.05时,芯体截面梯度变化的点阵夹层结构面比吸能和压溃载荷率达到最大值。
3 结 论
本文提出了一种可以提高点阵夹层结构吸能特性的新结构,即芯体截面梯度变化的点阵夹层结构,建立了该点阵夹层结构和传统点阵夹层结构极限承载力的计算方法,并分析了两种结构的变形特征,对比了两种结构吸能特性,得到如下结论:
(1) 在平压载荷作用下,传统点阵夹层结构芯杆存在一个主要的弯曲变形截面,即杆件的l/2处,芯体截面梯度变化的点阵夹层结构存在两个主要的弯曲变形截面,即杆长的l/8和l/4处,且芯体截面梯度变化的点阵夹层结构极限承载力小于传统点阵夹层结构。当α1<π/2和α2≈π/2+θ时,芯体截面梯度变化的点阵夹层结构达到极限载荷。
(2) 针对两种结构建立极限承载力的计算模型,通过与有限元分析结果进行对比,其最大误差为8.9%,说明该计算模型可以满足工程设计需要。
(3) 芯杆梯度化可以有效地提高点阵夹层结构面比吸能及吸能的稳定性,且当梯度化系数为0.05时,芯体截面梯度变化的点阵夹层结构吸能达到最大值。

