基于精细积分法的相邻结构弹塑性地震碰撞分析
张瑞杰, 李青宁, 王天利, 叶 毅, 孙建鹏
(西安建筑科技大学 土木工程学院, 西安 710055)
罕遇地震发生时,结构可能因较大的变形而产生开裂、屈服和相对滑动,从而使结构进入塑性状态。同时,因动力特性的差异或行波效应的影响,相邻结构的位移差值可能超过结构预留间隙,从而产生碰撞现象。这种相邻结构的碰撞,往往会产生巨大的破坏作用,如房屋建筑的垮塌、桥梁结构的局部损坏甚至落梁[1-3]。结构进入塑性状态是材料非线性问题,相邻结构碰撞是状态非线性问题。对于罕遇地震下相邻结构的地震时程反应分析,应同时考虑结构的弹塑性和碰撞。时程反应分析中的相邻结构碰撞模拟方法多采用接触单元法[4]。该方法是在两可能接触点之间添加具有一定刚度和阻尼特性的接触单元,当接触发生时激活接触单元。实质上该方法是将碰撞接触过程处理为碰撞力的作用过程,根据碰撞力计算假定的不同,发展了多种接触单元模型。
对于结构地震响应过程,区分为分离状态和碰撞状态,并且,对不同的状态可分别采用结构切线刚度矩阵建立增量动力平衡方程或割线刚度矩阵建立全量动力平衡方程。动力平衡方程的常用数值积分方法,有中心差分法、Newmark-β法、Wilson-θ法等方法。近年来,求解结构动力响应的精细积分法[5]的提出,为动力平衡方程的求解增添了新的思路,因而,一经提出就得到了众多学者的重视和发展,并很快推广到非线性动力平衡方程的求解[6]。申永康等[7]应用精细积分法对建筑结构的爆破地震反应进行弹塑性分析,郭泽英等[8]对精细积分进行改进,并将精细积分法应用于短肢剪力墙结构的弹塑性地震反应分析。张瑞杰等[9~12]将精细积分法引入到地震碰撞动力平衡方程的数值求解,但只适用两个单自由度的弹性碰撞问题。两个单自由度体系的弹性地震碰撞仅有一个接触单元,算法设计相对较简单。对于多个相邻结构,地震发生时,有多个可能的接触碰撞点,且结构可能进入塑性状态。该类结构可以简化为多个单自由度结构弹塑性多点碰撞模型,叠加了状态非线性和材料非线性问题。在前人研究的基础上,进一步将精细积分法推广到多个单自由度结构的弹塑性多点碰撞动力平衡方程的求解。
1 弹塑性碰撞动力平衡方程及其精细积分解法
1.1 弹塑性动力平衡方程
(1)
同时,结构反应满足全量动力平衡方程:
(2)
若t时刻为接触碰撞状态,全量动力平衡方程为:
(3)

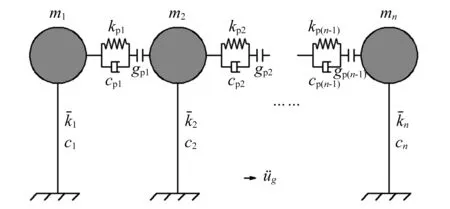
图1 单自由度结构多点碰撞模型Fig.1 Multi point collision model of SDOF structures
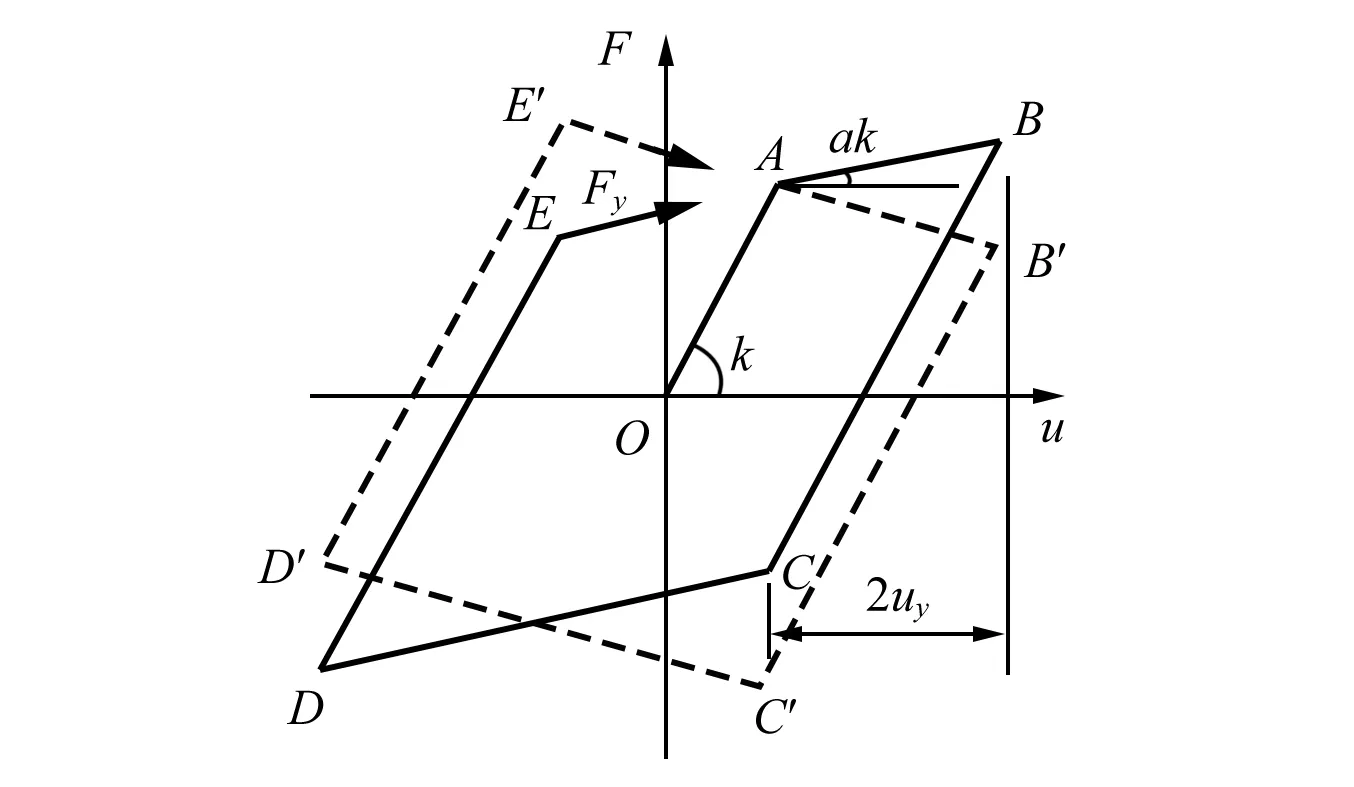
图2 不考虑刚度退化双直线模型Fig.2 Bi-linear model without considering stiffness degradation
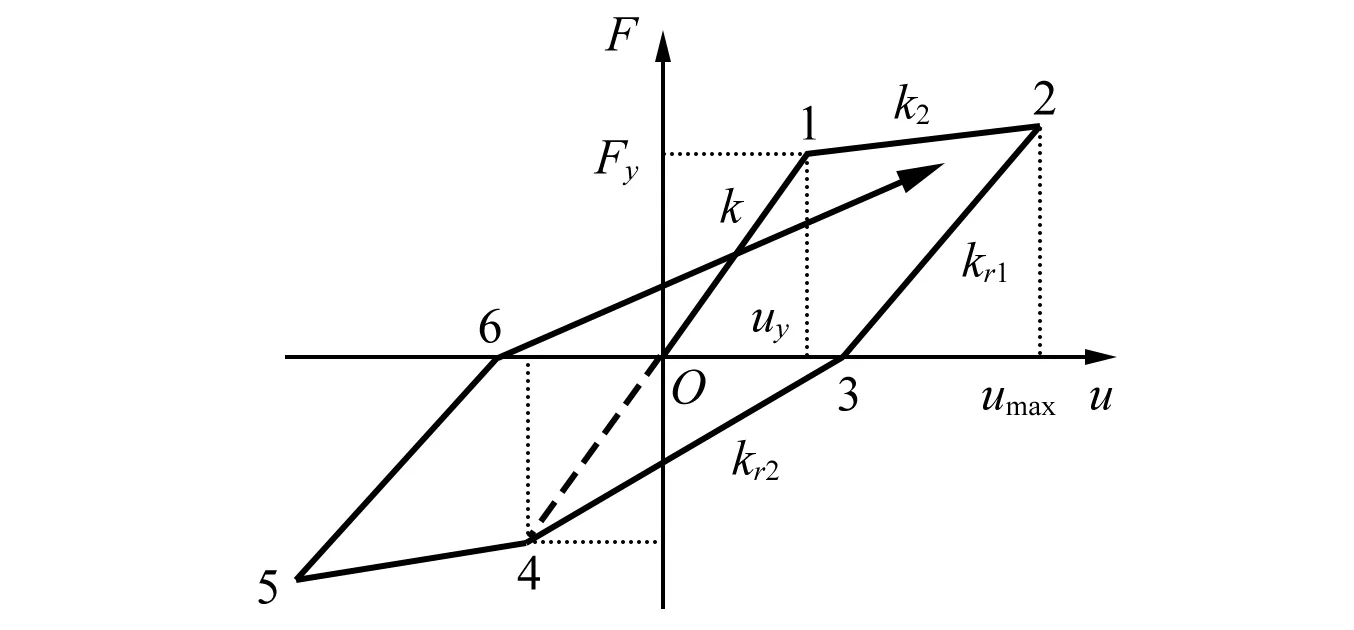
图3 考虑刚度退化双直线模型Fig.3 Bi-linear model considering stiffness degradation
1.2 分离状态增量动力平衡方程的精细积分法
首先讨论分离状态增量动力平衡方程的精细积分法。对方程(1)进行降阶,引入向量p,令
(4)
则有,
(5)
方程(1)可变换为:
(6)

(7)
式中:t时刻的系统矩阵H为:
(8)
在分离阶段,将积分过程分成时间步长为Δt的若干时间间隔,则Δtk=tk-tk-1、Δtk+1=tk+1-tk是相邻的两个时间步,已知Δtk时间步的增量状态时,Δtk+1时间步的增量状态为:
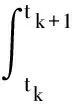
(9)
Δt时段内非齐次项按线性变化,满足:f(τ)=f(tk)+[f(tk+1)-f(tk)](τ-tk)/Δt=f(tk)+Δf(τ-tk),Δf表示非齐次项tk至tk+1时段的变化率。根据式(9)的解答可得vΔtk、vΔtk+1之间的转换关系。
vΔtk+1=T(tk)[vΔtk+H(tk)-1(f(tk)+H(tk)-1Δf)]-
H(tk)-1[f(tk)+H(tk)-1Δf+Δf·Δt]
(10)
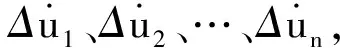
以上讨论针对增量动力平衡方程,对于全量动力平衡方程精细积分法求解原理是相同的。应注意,对于理想弹塑性模型切线刚度为0的屈服阶段,增量法是不适用的。精细积分法是一种显式的递推方法,对于增量动力平衡方程,是从前一个时间步的结构位移、速度、加速度增量,递推其后一时间步的位移、速度、加速度增量。这就要求,采用增量法的时间步长应该相等,且前一个时间步的增量状态已知。当前时刻的位移、速度、加速度是之前积分步长增量累加结果,应同时满足结构全量动力平衡方程(2)。同样的,通过全量动力平衡方程精细积分法递推出结构位移、速度、加速度后,也可计算出时间步内结构位移、速度、加速度的增量,满足增量动力平衡方程(1)。这是全量法和增量法能够混合使用的理论基础。
1.3 碰撞动力平衡方程精细积分法
接触单元模型的碰撞力可分解为弹性恢复力和阻尼力两部分,弹性恢复力表达为碰撞弹簧刚度与侵彻位移的乘积,阻尼力表达为阻尼系数与速度差的乘积。根据碰撞弹簧刚度和阻尼系数的不同假设,诞生了不同的接触单元模型,如线性弹簧模型[14]、线性弹簧-阻尼(Kelvin-Voigt)模型[15]、Hertz模型[16]、非线性弹簧阻尼(Hertz-damp)模型[17]、Jan-Hertz-damp模型[18-19]。这些接触单元的碰撞力可统一表达为:
(11)
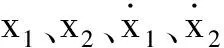
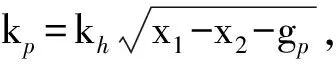
(12)
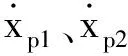
基于大量的碰撞试验,Jankowski认为接触碰撞阶段可划分为接近阶段和恢复阶段,能量损失主要发生在接近阶段。基于此,对Hertz-damp模型的阻尼力项进行了改进,即Jan-Hertz-damp模型。该模型仍可表达成式(11)形式。式中阻尼系数cp为:
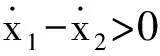
(13)
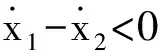
cp=0
(14)
假设时刻图3模型中所有接触点均为接触碰撞状态,方程(3)中碰撞力列向量的表达式为:
(15)
对于更一般的接触碰撞情况,假设n-1个接触单元中的第i个接触点未产生接触碰撞,只需将式(15)中kpi、cpi置为0即可。以往情况下式(15)作为方程2的非齐次项处理。由于求解时刻的位移、速度未知,采用前一时间步的位移、速度来近似计算碰撞弹簧刚度、阻尼系数以及碰撞力。这里介绍另一种处理方式,将式(15)代入方程(3),其中碰撞力的弹性恢复力在左端进行分解并与结构恢复力项合并,而阻尼力仍作为非齐次项处理,由前一时间步位移、速度近似计算。对于线性弹簧模型和Kelvin-Voigt模型完全消除了弹性恢复力项的迭代误差。之所以将阻尼力作为非齐次项处理,是因为对于Kelvin-Voigt模型,阻尼力是突变的,而Jan-Hertz-damp阻尼模型阻尼力是位移差和速度差的函数,在碰撞开始时刻迅速增大,随后减小。实践证明,这两种模型将阻尼力作为未知量在左端分解,会引起数值计算的不稳定。经过处理后,碰撞动力平衡方程(3)进一步写为如下形式:
(16)
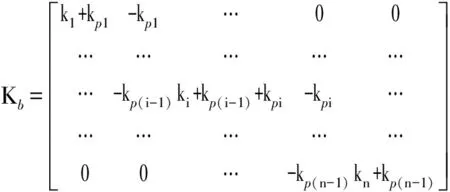
对碰撞动力平衡方程(16)的精细积分法推导过程与方程(1)类似,不再赘述。碰撞状态的动力平衡方程也可以采用结构切线刚度矩阵建立成增量形式,但要求在第一个时间步采用全量法精细积分,获得增量方程精细积分的启动条件。由于碰撞持续过程非常短暂,结构割线刚度变化较小,所以体现不出增量法的优势。
1.4 界点的处理
对于n个单自由度弹塑性结构,均可定义独立的弹塑性模型。以图1所示不考虑刚度退化的双直线模型为例说明,在载荷过程中,存在A、B、C、D、E界点。A界点是弹性阶段正向加载时屈服点;B界点是正向屈服至反向卸载阶段界点,判断条件是速度由正变负;C界点是反向卸载屈服界点;D界点是反向卸载至正向加载界点,判断条件是速度由负变正;E界点是正向加载屈服界点。在界点处结构反应满足连续性条件。当荷载处于OA弹性状态时,求解可以采用全量法进行。当荷载通过A界点进入塑性状态时,为避免迭代可采用增量法求解,但应注意理想弹塑性模型切线刚度为0的屈服阶段不适用。在当前时刻,根据精细积分求解的结构位移、速度,可对各结构弹塑性阶段进行判断。当结构弹塑性阶段改变,即意味着界点产生。为了精确吻合滞回曲线,需要对界点产生的时刻以及界点处的结构反应进行精确分析。
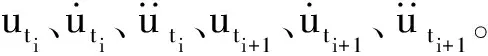
(17)
而B、D界点,判定条件是ti+τ时刻速度为0,可建立如下方程:
(18)
方程式(17)为一元三次方程,可采用二分法求解[0 Δt]内的解。方程式(18)为一元二次方程,可直接求解[0 Δt]内的解。ti+τ时刻即为精准界点产生时刻,进而可按线性加速度假定求解该时刻的位移、速度、加速度。舍弃ti+1时刻求解结果,存储ti+τ时刻结果。采用增量法时,由于通过界点后的第一个时间步的增量状态未知,应通过全量法迭代求解一次,为增量法的启动创造初始条件。
1.5 分离碰撞状态转换
将结构反应过程分为分离状态和接触碰撞状态,两种状态下的积分步长分别为Δt1、Δt2。精细积分法对步长不敏感,对分离状态积分步长设定的可以大些。而对于接触碰撞阶段,由于碰撞过程本身很短暂,要采用较小的积分步长,该步长取值可通过试算后确定。
为进一步提高计算精度,需要精准的找到开始接触和分离的时刻。假定ti时刻第k个接触单元uk-uk+1-gpk<0(没有接触),而ti+1时刻uk-uk+1-gpk>0(已经接触),说明接触开始时刻ti+τ介于时刻ti至ti+1时刻之间。已解出ti时刻和ti+1时刻的位移、速度、加速度。根据线性加速度假定,ti+τ时刻的位移满足:
(19)
方程(19)为一元三次方程,可以利用二分法求解τ在区间[0 Δt]内的解,ti+τ时刻即为碰撞起始时刻。程序设计时,需要在每一步递推前对n-1个接触单元循环判定是否接触。一旦判定有分离-接触碰撞状态转换,首先求解精确的碰撞时刻ti+τ和该时刻的结构反应,舍弃ti+1的结果。从ti+τ时刻积分步长变为接触碰撞阶段的积分步长,进入碰撞阶段求解。接触碰撞状态至分离状态转换的分离时刻可以采用同样的原理计算。
需要注意的是,由于是多点碰撞,在当前积分点可能有多个接触点同时转为接触碰撞状态,也可能在当前接触点未分离的情况下有新的接触点进入接触碰撞状态。对多接触点判定产生接触情况,通过求解各自的精确碰撞时刻,以最小值作为状态转换时刻。接触点分离时,每一接触点分离均求解精确分离时刻。所有接触点均分离后,步长变化为分离状态的步长。同时,对于每一积分步接触单元状态的判定作为组集刚度矩阵的依据,未产生碰撞的接触单元相应的弹簧刚度系数、阻尼系数置为0。对于结构割线刚度,应在每一积分步迭代求解。
2 算法设计
单自由度多点弹塑性地震碰撞分析程序设计较为复杂,整体上划分为分析准备阶段和积分计算阶段。算法具体流程见图4。
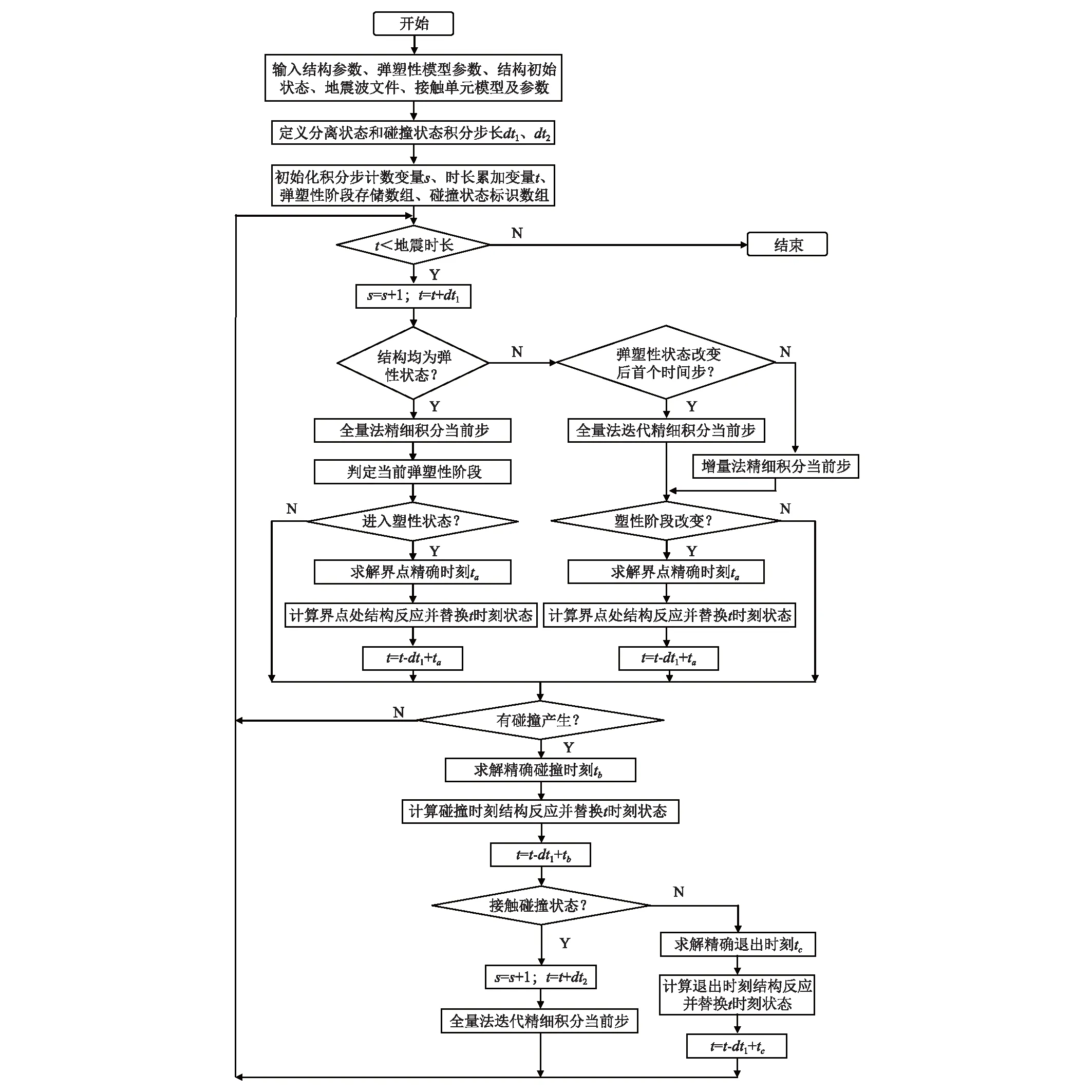
图4 单自由度弹塑性结构多点地震碰撞算法流程图Fig.4 Flow chart of multi point seismic collision algorithm for elastic-plastic SDOF structures
3 算例验证
某三跨简支梁桥墩梁间采用盆式橡胶支座,一端纵向固结一端活动,力学图式见图5。该模型简化为三个单自由度体系,有两个可能的邻梁碰撞点,采用Kelvin-Voigt接触单元模型。桥墩的弹塑性模型假定为不考虑刚度退化的双直线模型。该例的结构参数、双直线模型参数、接触单元模型参数见表1。沿纵向输入1940年El-Centro地震动记录NS分量。该地震动记录持时53.73 s,峰值加速度调整为0.5 g,地震波步长0.02 s。
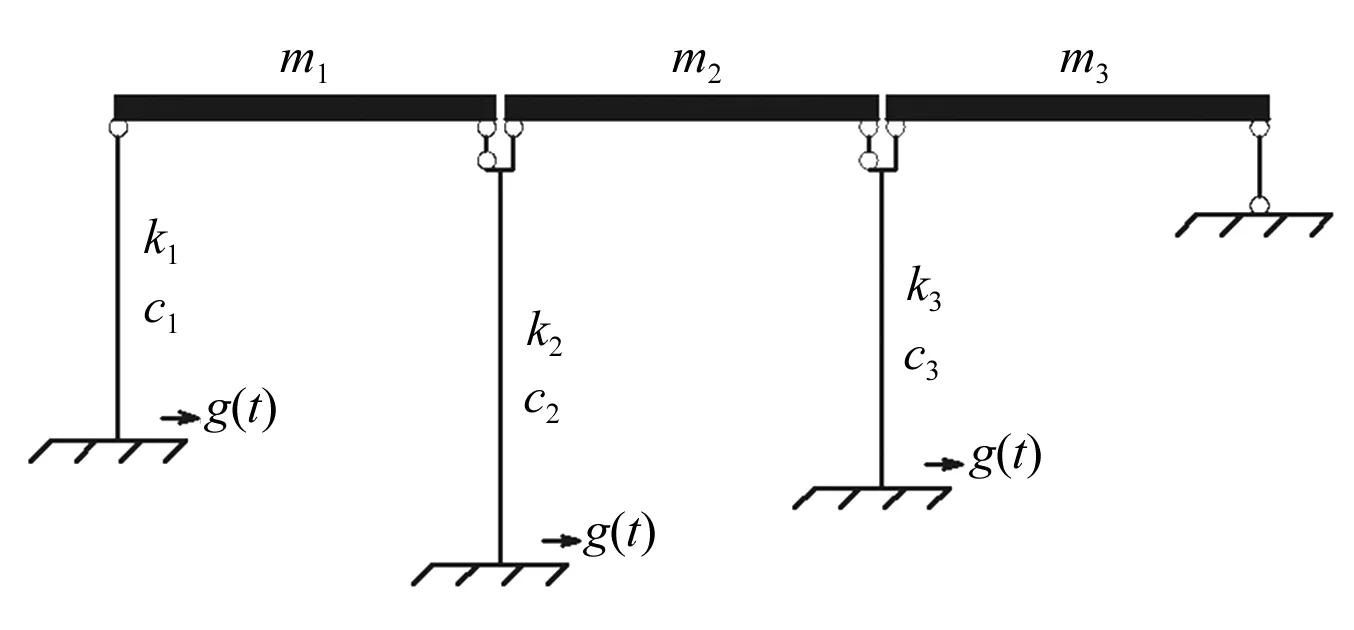
图5 某三跨简支梁地震碰撞模型Fig.5 The earthquake collision model of three spans simply supported beam

结构参数结构质量m/kg初始刚度k/(N·m-1)阻尼比/%双直线模型参数屈服位移屈服后刚度接触单元参数碰撞刚度kP/(N·m-1)恢复系数e间隙gP/m1221 0004.8×10750.044.8×1062221 0001.9×10750.071.9×1063221 0003.2×10750.063.2×1064.7×1090.650.084.7×1090.650.08
采用精细积分法分析时,设定三结构分离状态积分步长为0.002 s,接触碰撞状态为0.000 2 s。同时为验证算法的正确性,采用Ansys软件进行弹塑性地震反应分析,积分步长为0.001 s。其中单自由度结构和接触单元均采用Combin40非线性弹簧单元模拟。
图6~图9分别给出了两种方法分析的三跨简支梁的相对位移时程、加速度时程、结构滞回曲线、碰撞力时程。对比两种方法的计算结果,相对位移时程曲线、加速度时程曲线、碰撞力时程曲线均是重合的。两方法分析的三跨结构的位移极值相差小于1%,结构1~结构3最大加速度值相差4.2%、1.5%、1.5%,最小值相差1.7%、1.4%、3.2%,接触点1和接触点2最大碰撞力值相差分别为0.7%、1.9%。滞回曲线对比表明,两种方法滞回曲线趋势一致,精细积分法具有更清晰的界点,结构滞回曲线完全符合不考虑刚度退化的弹塑性模型假定。通过Ansys验证表明,弹塑性结构多点碰撞程序计算结果准确,且计算速度更快。
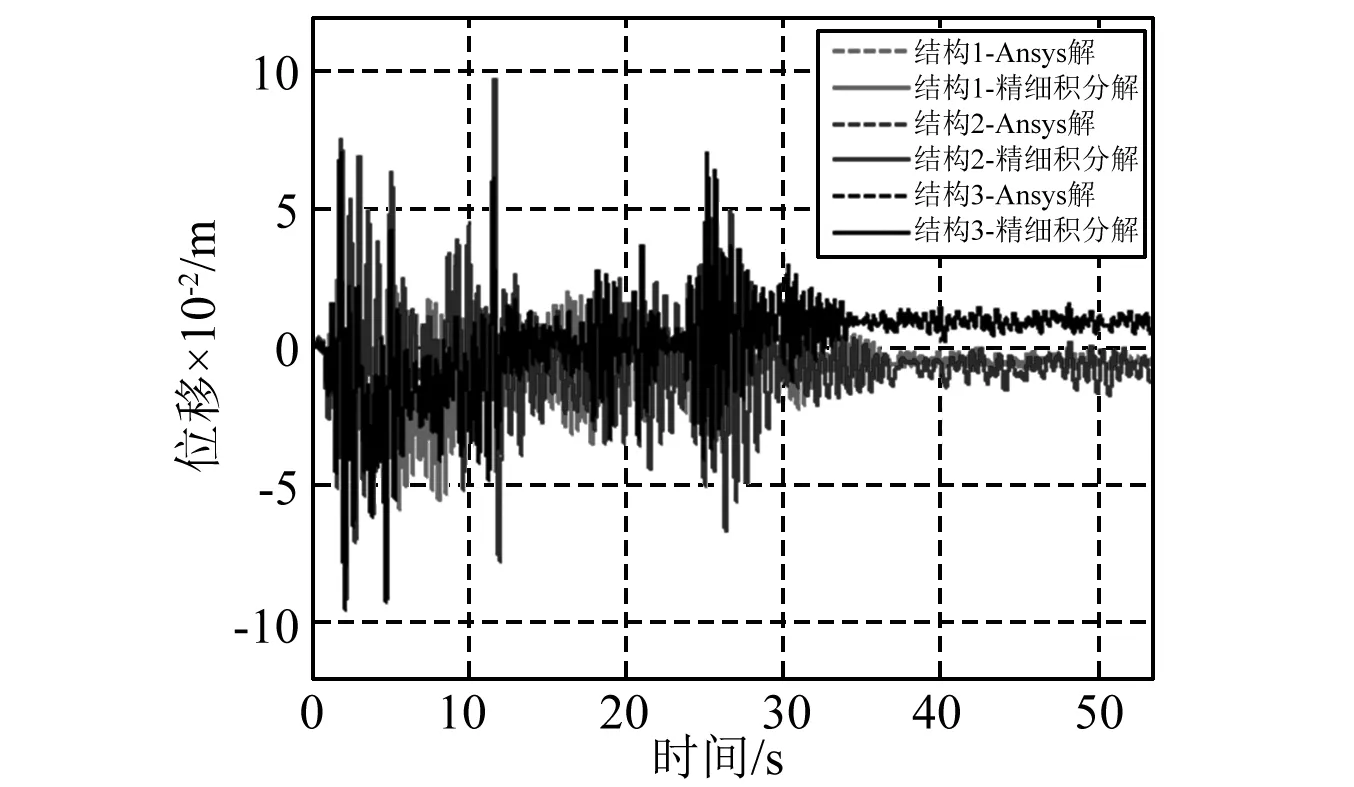
图6 三跨简支梁位移时程Fig.6 Displacement time history of the three spans simply supported beam
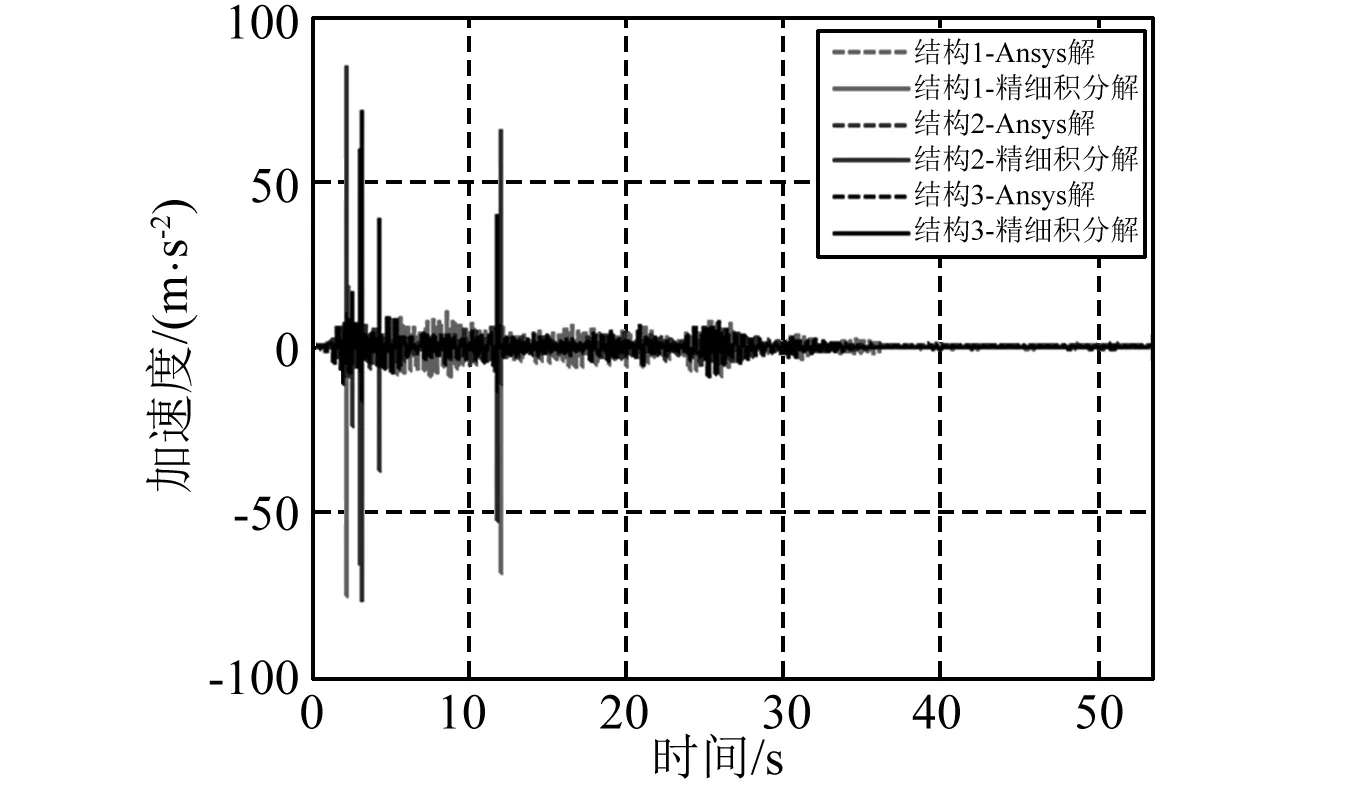
图7 三跨简支梁加速度时程Fig.7 Acceleration time history of the three spans simply supported beam
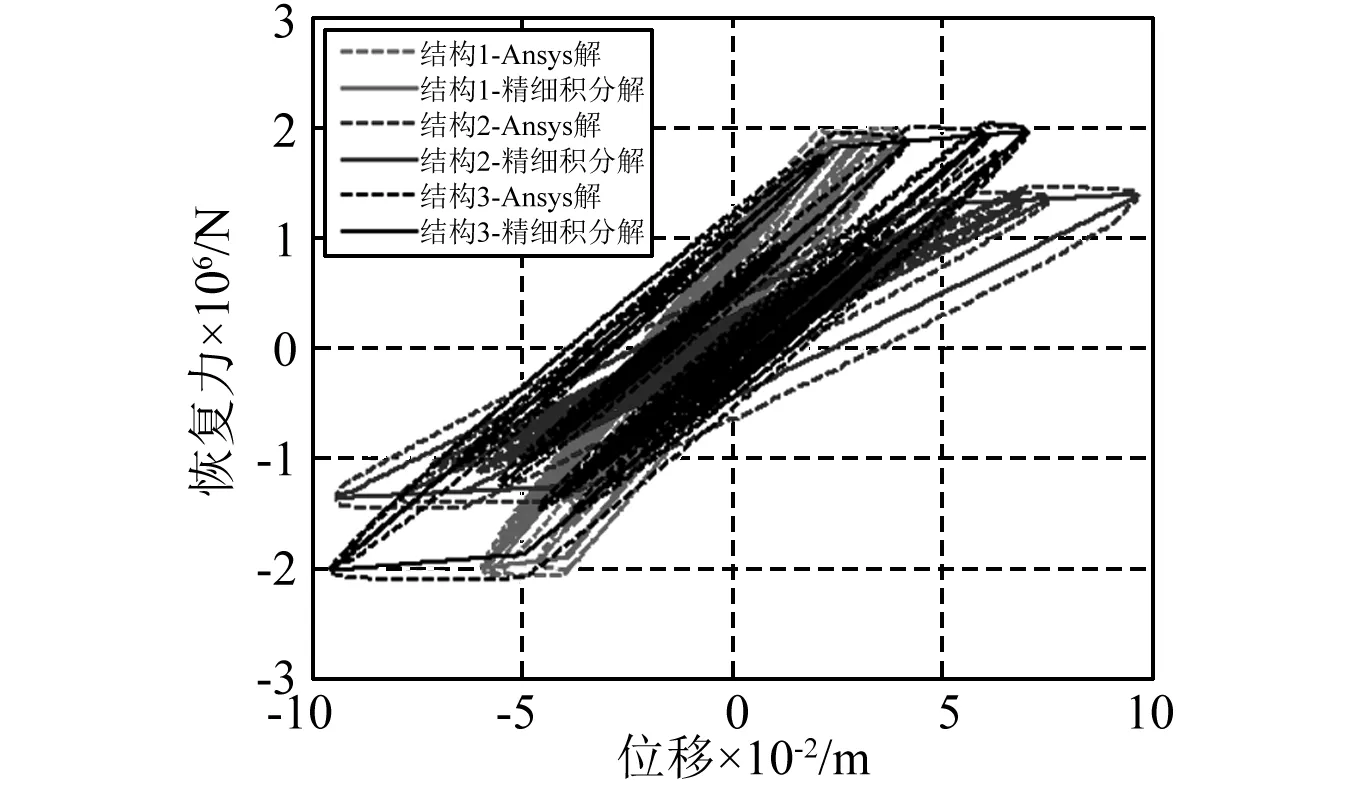
图8 三结构的滞回曲线Fig.8 Hysteretic curve of three structures
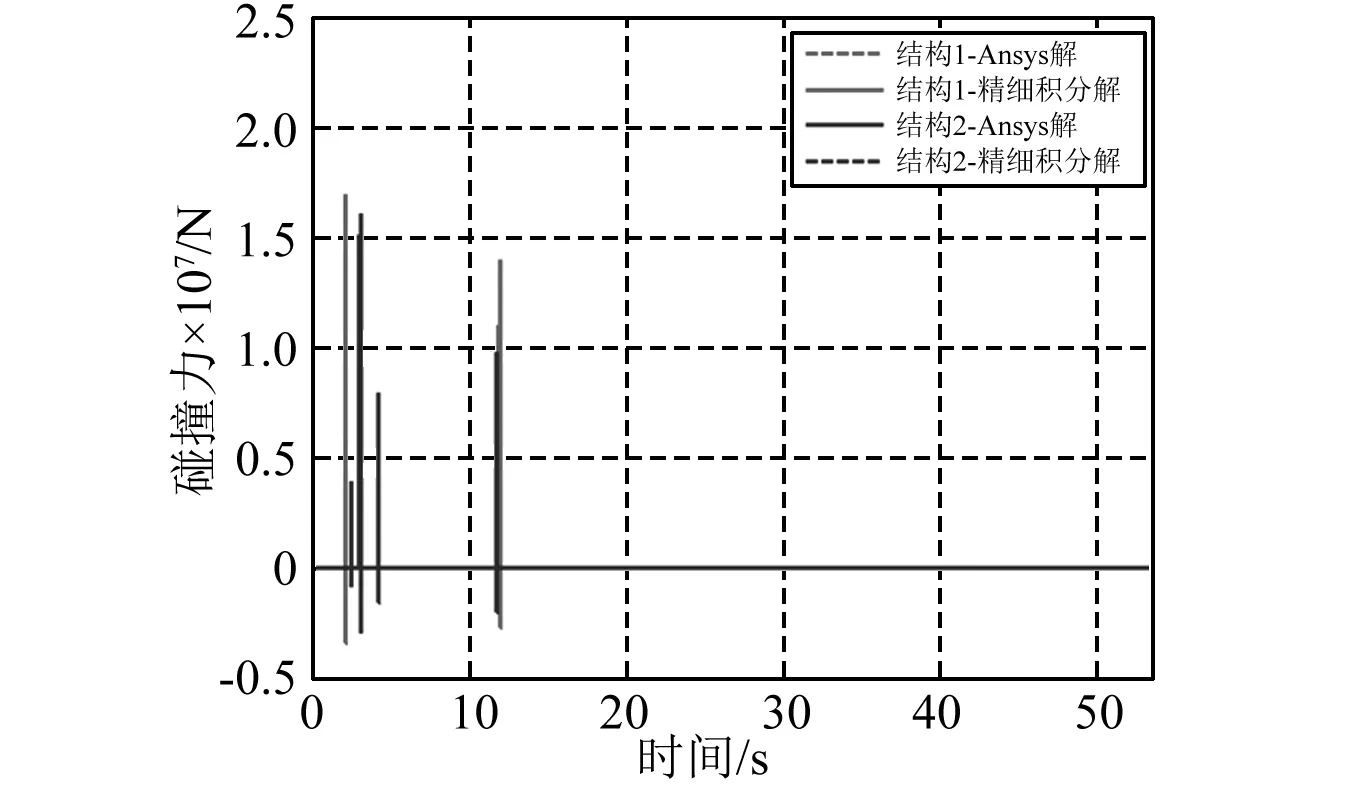
图9 两接触点碰撞力时程Fig.9 Pounding force time history of the two contact points
地震结束后结构并没有恢复到最初位置。这是因为,当结构位移超过屈服位移时,即进入塑性状态,恢复力与位移呈现非线性关系,并且卸载后结构有残余变形。当两相邻结构的相对位移差值超出结构间隙时,两结构即发生碰撞,接触点1产生2次碰撞、接触点2产生4次碰撞,6次碰撞的接触持时0.015 5~0.016 4 s。本例接触碰撞阶段的积分步长约为接触持时的1/80,能精确的模拟结构的接触碰撞过程。从加速度时程可以分析出,碰撞时结构的加速度急剧变化,碰撞力远大于结构恢复力,这对于易受冲击损坏的伸缩缝、固定支座、梁端、桥台背墙等是非常不利的。
4 接触单元参数影响分析
Kelvin-Voigt接触单元模型输入参数包括碰撞弹簧刚度、间隙和恢复系数,其中恢复系数决定阻尼特性。为研究碰撞弹簧刚度、间隙和恢复系数对结构碰撞的影响,对于图5结构假定了2组碰撞刚度、3组结构间隙、3组恢复系数,组合了18组接触单元模型参数,地震输入和结构参数不变。表2给出了18组不同接触单元参数对应的两个接触点的碰撞次数、碰撞力峰值。
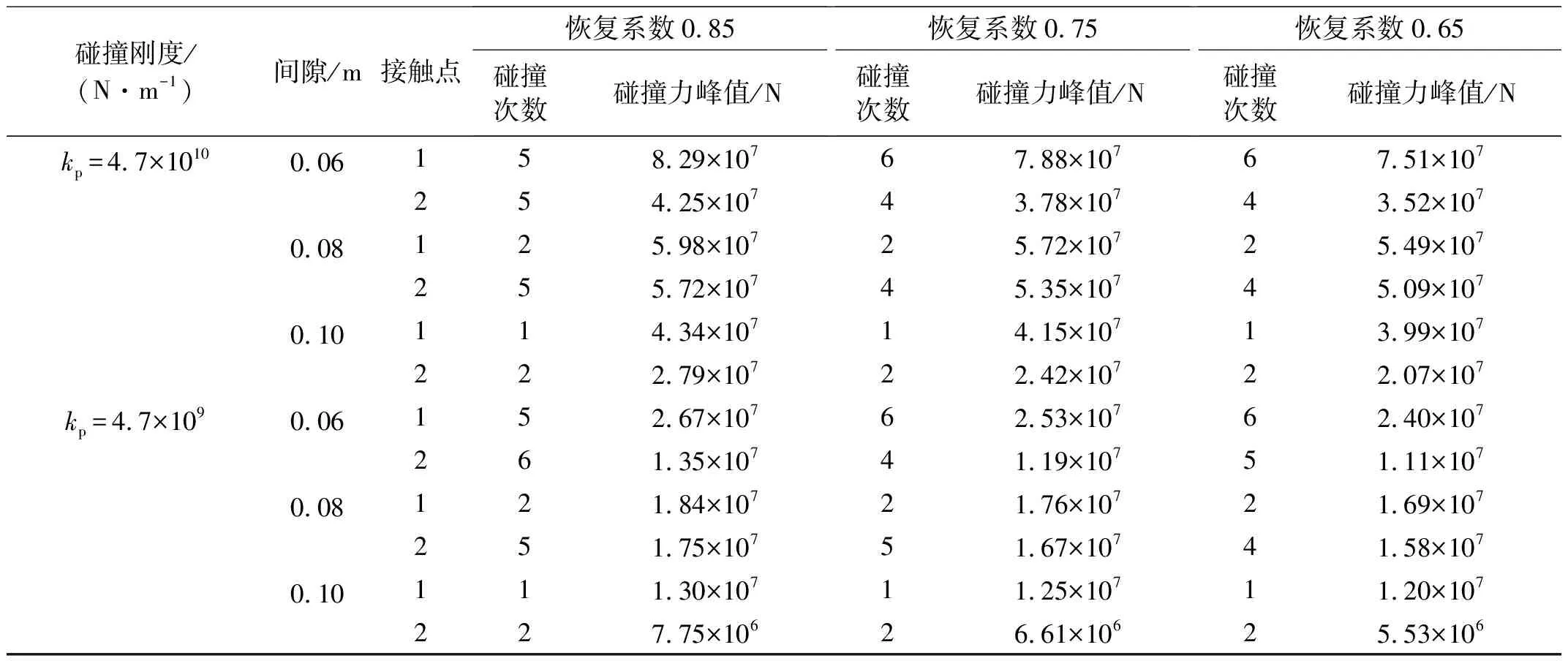
表2 不同接触单元参数地震碰撞分析结果对比
分析表2数据发现:刚度参数、恢复系数不变时,随着结构间隙的逐渐增加,碰撞发生的次数逐渐减少,结构的碰撞力峰值没有明确一致的变化规律。如间隙从0.06 m增加到0.08 m,接触点1碰撞力峰值减小而接触点2碰撞力峰值增加;增加到0.10 m,两接触点碰撞力峰值均减小。刚度参数、结构间隙不变时,随着恢复系数的减小,意味着碰撞阻尼增加,碰撞发生的次数基本不变,碰撞力峰值均减小。恢复系数从0.85减小为0.75,接触点1的碰撞力峰值减小了3.8%~5.2%,接触点2的碰撞力峰值减小4.6%~14.7%;减小为0.65,接触点1的碰撞力峰值减小了7.7%~10.1%,接触点2的碰撞力峰值减小9.7%~28.6%。结构间隙、恢复系数不变时,接触单元碰撞刚度减小1个数量级,碰撞次数基本不变,而碰撞力峰值大幅度减小。接触点1碰撞力峰值减小了67.8%~70.0%,接触点2碰撞力峰值减小了68.2%~73.3%。
由上述分析可推知:增加结构的间隙可以减小碰撞发生的可能性,甚至消除碰撞现象;而当碰撞不可避免发生时,通过增加柔性缓冲装置,可大幅度降低碰撞力,从而减小碰撞对结构的影响;增加碰撞过程的阻尼对于消减碰撞次数碰撞力意义不大。
6 结 论
(1)精细积分法是显式的递推方法,适用于求解弹塑性结构多点地震碰撞问题。结构进入塑性状态后,增量动力方程精细积分可以避免全量方程的迭代求解和割线刚度为0或无穷大情况下的数值求解困难。在界点处,通过精确求解界点转换时刻和对应的状态,使得结构的滞回曲线完全符合不考虑刚度退化的双直线弹塑性模型假定。
(2)结构碰撞过程非常短暂,通过全量方程精细积分法求解。为分离状态和接触碰撞状态设定了两种积分步长,兼顾了整体计算效率和碰撞计算精度。并且,通过求解精确的分离碰撞状态转换时刻和对应的状态,从而能够精确模拟结构的碰撞行为,得到符合接触单元模型假定的碰撞动力响应。
(3)通过对三跨简支梁算例进行Ansys分析,结果验证了多点弹塑性碰撞精细积分算法和程序的正确性。
(4)三跨简支梁地震碰撞分析表明,碰撞使得结构加速度在短时间内急剧变化,桥梁伸缩缝、固定支座、梁端、桥台背墙等易受冲击损坏。
(5)对接触单元模型参数分析表明:增加结构的间隙可以减少碰撞发生的次数,甚至消除碰撞现象;而当碰撞不可避免发生时,通过增加柔性缓冲装置,可大幅度降低碰撞力,从而减小碰撞对结构的影响。

