分布式光伏电站中汇流箱布置方法及案例分析

浙江正泰新能源开发有限公司 ■ 陈明月 周承军 江伟 吴云来 李建周 沈道军

0 引言

近年来，随着国家政策对新能源的大力支持，分布式光伏已成为光伏未来发展的新趋势，特别是在2017年，分布式光伏项目已成为各投资建设企业主要投建的光伏电站类型。因此，分布式光伏电站设计的经济性、合理性，以及方案的最优化已成为各大企业需要研究的重点。其中，汇流箱的布置将影响整个分布式光伏项目的设计。最佳汇流箱布置方案可以减少整个分布式光伏项目的电缆投资成本，同时减少电缆损耗，提高系统的发电效率。

之前有研究者利用曼哈顿算法建立数学模型[1]，解析出方阵内汇流箱的最优位置的选取方法，但该方法较适用于大型地面光伏电站；对于屋顶分布式光伏电站而言，由于屋顶的复杂性，设备可能无法安装在用此方法得出的最优位置。所以，本文以曼哈顿算法为基础，结合屋顶分布式光伏电站的特殊性，通过解析数学模型，以实际案例为分析依据，研究出光伏方阵外的汇流箱的最优布置方法。

1 分布式光伏电站中汇流箱的布置对系统的影响

电缆压降计算公式为：

其中，ρ为铜的电阻率；L为电缆的长度；I为电流；S为电缆截面积。

由式(1)可知，光伏方阵至汇流箱及汇流箱至配电柜的距离越大，压降就越大，线损也越大[2]，整个系统的发电量损失增大，发电效率降低。同时，若汇流箱的位置不合理，集电线路距离较长，也会增加电缆的投资成本[3]。

2 方阵内汇流箱位置选取方法对于屋顶分布式光伏项目的局限性

在参考文献[4]中，作者利用曼哈顿算法建立数字模型分析出了方阵内汇流箱的位置，但通常情况下，屋顶分布式光伏项目方阵内部是不会安装汇流箱的，主要原因有以下几点：

1)汇流箱在方阵中不好安装。组件在彩钢瓦屋顶上安装时需平铺或小倾角安装，而在混凝土屋顶带倾角安装后，支架后立柱高度通常仅为60～70 cm，由于后立柱高度有限，所以汇流箱不能像在地面电站那样挂装在后立柱上。

2)汇流箱在方阵中安装会产生阴影。组件在混凝土屋顶带倾角安装后，支架前立柱通常约为20 cm。因此，当汇流箱通过支架固定安装在方阵中间时，可能会对组件产生阴影，影响系统的发电效率。

3)汇流箱一般都会选择就近挂装在屋顶的女儿墙上，这样做既相对可靠，又便于安装，同时省去了制作汇流箱支架的成本。但若挂装于女儿墙上，汇流箱一般都位于光伏方阵之外。

综合以上几点，对于屋顶分布式光伏项目，方阵内汇流箱的位置选取存在局限性。

3 方阵外单个汇流箱位置选取方法

3.1 方阵外单个汇流箱位置选取模型解析

汇流箱位置选取以光伏电缆用量最少为目标。假设在平面内光伏方阵中有n个组串，每个组串有正、负极输出，建立平面坐标系(坐标的原点为任意位置)，则每个输出端的坐标已知，一共有2n个坐标点，假设第i个点的坐标为(xi，yi)，其中i=1，2，3…，2n。对 2n个坐标从小到大进行排序后分别为(x1，y1)，(x2，y2)…(x2n，y2n)。以x坐标为例，如图1所示。

图1 x坐标系

图2 方阵内汇流箱位置

在屋顶分布式光伏项目中，若汇流箱在方阵外部，汇流箱布置坐标的选择通常有以下几种情况，其中，阴影区为方阵区域，坐标点为汇流箱的位置坐标。

1)汇流箱的位置坐标(xp，yp)分别在x1～x2n以外，y1～y2n以外，如图3a所示。

2)汇流箱的位置坐标(xp，yp)分别在x1～x2n以内，y1～y2n以外，如图3b所示；

3)汇流箱的位置坐标(xp，yp)分别在x1～x2n以外，y1～y2n以内，如图3c所示。

则在坐标系中存在一个p点，坐标为(xp，yp)，到这2n个坐标点的直线距离之和L(xp，yp)最小。即当满足式(2)：

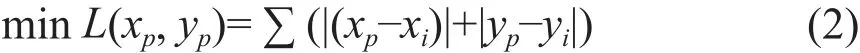
这个p点即为汇流箱的最佳位置坐标[5]。

当汇流箱在方阵内部其位置坐标(阴影区为方阵区域，坐标点为汇流箱的位置坐标)如图2所示。

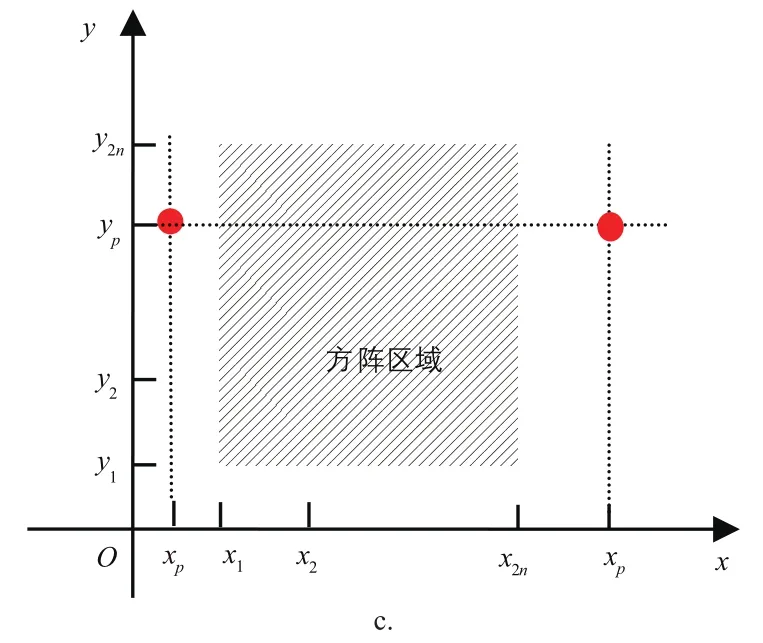
图3 方阵外汇流箱位置

当p点在图3a所示的情况时，p≤1或p≥2n，则目标函数式为：

去掉绝对值，则：

根据单调性，式(7)为增函数，当xp无限趋近于x2n时，L(xp)最小；式(8)为减函数，当xp无限趋近于x1时，L(xp)最小。所以当xp∈(x2n,+∞)时，则xp→x2n，L(xp)最小；当xp∈(-∞,x1)时，则xp→x1，L(xp)最小；同理，当yp∈(y2n,+∞)时，则yp→y2n，L(yp)最小；当yp∈(-∞,y1)时，则yp→y1，L(yp)最小；

当p点在图3b所示的情况时，即当xp∈[x1,x2n]时，

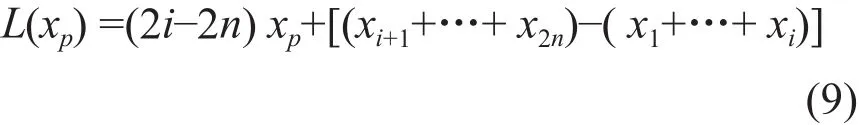
式(9)中，当i=n时，xp∈[xn,xn+1]，L(xp)值为最小[1]；

同理，当p点在图3c所示的情况时，即当yp∈[y1,y2n]时，

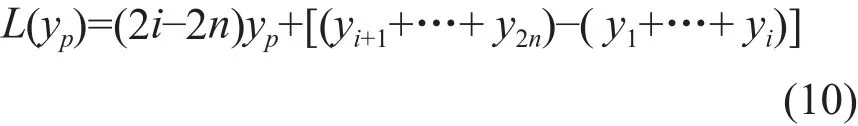
式 (10)中，当i=n时，yp∈[yn,yn+1]，L(yp)值为最小[1]。

当p点x坐标分别为xp∈[x1,x2n]和xp∈(x2n,+∞)U(-∞,x1)时，哪种情况的L(xp)min更小？下文就这两种情况进行了比较。

所以，p点x坐标为xp∈[x1,x2n]时，L(xp)min比p点x坐标为xp∈(x2n, +∞)U(-∞,x1)时的情况要小；y轴坐标同理。

3.2 方阵外单个汇流箱位置选取方法总结

在分布式光伏项目设计过程中，放置在方阵外的汇流箱在直角坐标系中，一般情况下xp或yp坐标不在方阵区域内，就如图3a、图3b、图3c所示的情况。

xp∈(x2n,+∞)或xp∈(-∞,x1)，yp∈(y2n,+∞)或yp∈(-∞,y1),xp、yp的取值范围需要根据现场的实际情况而定，比如业主配电房的方位、分站房的方位，或者挂装女儿墙的方位等初步确定xp和yp的范围，再确定xp或yp的最优解。在初步选取xp和yp的范围时，根据现场实际情况尽量将xp或yp选取在组串正负极x坐标或y坐标以内。

方阵外的汇流箱位置情况大体归纳为图3a、图3b、图3c所示3种情况，这3种情况的(xp，yp)最优解如下：

图3a所示情况中，当xp∈(x2n,+∞)，则xp的最优解为无限趋近于x2n的值；当xp∈(-∞,x1)，则xp的最优解为无限趋近于x1的值；当yp∈(x2n, +∞)，则yp的最优解为无限趋近于y2n的值；当yp∈(-∞,y1)，则yp的最优解为无限趋近于y1的值；

图3b所示情况时，当yp∈(y2n,+∞)，则yp的最优解为无限趋近于y2n的值；当yp∈(-∞,y1)，则yp的最优解为无限趋近于y1的值；xp∈[x1,x2n]，当i=n时，xp的最优解为xn和xn+1区间的值；

图3c所示情况中，当xp∈(x2n,+∞)，则xp的最优解为无限趋近于x2n的值；当xp∈(-∞,x1)，则xp的最优解为无限趋近于x1的值；yp∈[y1,y2n]，当i=n时，yp的最优解为yn和yn+1区间的值。

图4 实际屋顶光伏方阵排布图

4 案例分析

4.1 案例项目情况介绍

以某屋顶分布式光伏项目为例，对以上推论进行验证。屋顶光伏方阵排布情况如图4所示，其中，A、B、C、D为汇流箱的放置位置。该项目业主的配电房在屋顶的西侧靠南，女儿墙的高度为2 m，该方阵南面有另外的方阵，初步可以判定汇流箱放置于屋顶的西边。此项目使用280 Wp的多晶硅组件，组件的峰值电压Vmpp为31.48 V。20块组件为一串，图4方阵中共16串组串，经过16进1出的汇流箱汇流，所以此时n=16。

4.2 汇流箱最佳位置坐标确定

利用计算机辅助设计(CAD)确定ZC010101～ZC010116组串正负极的坐标，共有32个坐标；对32个x坐标及32个y坐标进行排序，其中，x1=0.018，x16=17.504，x17=24.176，y1=0.465，y16=10.605，y17=10.605。所以当汇流箱可以放置在方阵内部时，汇流箱的最佳x坐标在[17.504，24.176]区间内，最佳y坐标为10.605。则汇流箱位置大致在图4中的A处。但放置在A处，会对北边的组件产生阴影影响。

表1 3种方案电缆用量及投资对比

根据现场的实际情况，汇流箱位置初步定在屋顶西侧，由此可确定xp∈(-∞,x1)，yp∈[y1,y2n]，符合图3c所示情况。所以，xp取无限趋近于x1的值，即xp取趋近于0.018且小于0.018的值；yp取值为y16与y17区间的值，即yp=10.605。此时可得出汇流箱的最佳位置在图4中的B处。

4.3 汇流箱位置选取的不同方案对比

若汇流箱在图4中C、D的位置，此时汇流箱的位置在方阵以外的范围，通过上文的推理可知，光伏专用电缆用量B处＜C处＜D处。将汇流箱分别在B、C、D处3种方案的直流光伏电缆的用量、直流电缆的用量、电缆总投资及线损的数据进行分析比较，分析数据如表1、表2所示。其中，PV1F 1×4 mm2电缆费用(包含施工费和材料费)为5.5元/m，ZC-YJV-0.6/1kV-2×95 mm2电缆费用(包含施工费和材料费)为109元/m。

表2 3种方案电缆线损对比

由表1、表2可知，从成本上看，B方案电缆投资最少，从电缆的线损上看，其线损也是最小。所以最优的汇流箱的布置位置可以节省项目的投资成本，同时可提高项目的发电效率。

5 结语

屋顶分布式光伏项目汇流箱布置的设计是设计过程中非常重要的环节，对项目的投资成本和发电效率有重要作用，所以在设计过程中，汇流箱位置的选取应尽可能使电缆成本最小，系统发电效率最大。由于方阵内汇流箱布置方法在屋顶分布式光伏项目中存在局限性，所以本文根据屋顶分布式光伏项目的实际情况，总结出方阵外汇流箱布置的3种可行情况，并对此3种情况的汇流箱选址方法进行了总结，为今后屋顶分布式光伏项目汇流箱的选址提供了设计依据和参考。当然，在实际情况中，屋顶项目有很多未知的复杂性，所以在设计过程中，还需综合考虑现场实际情况及整体方案的经济性来确定汇流箱的布置方位。