有压进水池消涡导水锥研究
蒋红樱,成 立,颜红勤
(1.江苏省水利工程科技咨询股份有限公司,南京 210029;2.扬州大学水利与能源动力工程学院,江苏 扬州 225009)
泵站进水池的作用是将泵站前池的水流引入水泵叶轮,确保水流在进水池完成转变,并且平顺的进入叶轮室。目前国内外学者主要集中于对开敞式进水池的水动力性能分析、水力效率数值优化、模型试验方面的研究。成立等[1]利用数值模拟得到开敞式进水池几何参数。钱义达等[2]进行了开敞式进水流道的实验研究,并给出了相应的几何参数。王本成等[3]利用数值模拟结合水动力性能研究了喇叭管悬空高的具体影响。陆林广等[4]进一步研究开敞式进水池并完成水力性能优化。何婷婷等[5]对开敞式进水池后壁形状进行了研究。关于有压进水池的研究相对于箱涵式进水流道以及开敞式进水池的数值模拟和试验研究要少很多[6,7]。陈松山[8]和周济人等[9]进行箱涵式进水流道试验方面的研究,同时也增设相关整流措施。杨帆等[10]采用CFX软件对双向立式轴流泵装置水力性能进行分析。本文结合某泵站工程,研究了不同导水锥的形式和尺寸对有压进水池水力性能影响。
1 封闭式进水池几何参数
封闭式进水池泵站包括进水池、叶轮、导叶以及90°弯管衔接的出水池,立式轴流泵装置模型如图1所示。
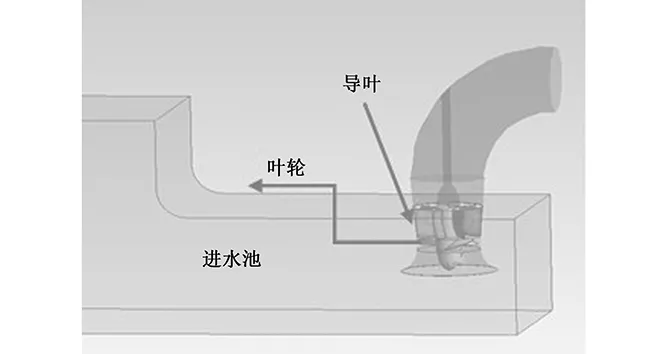
图1 封闭式进水池
叶轮的叶片数为3,叶片安放角为0°,叶轮直径为1 200 mm,转速为370 r/min;导叶的叶片数为7。单泵流量为5 m3/s。
典型的封闭式进水池为矩形结构形式,即后壁形状为矩形。进水池宽度B、后壁距T、喇叭管悬空高C,如图2所示。图中DL为吸水喇叭管口直径,本文DL=1 200 mm,进水池各几何参数以DL为基本参数表示。

图2 封闭式进水池结构形式
2 数值计算
2.1 控制方程
采用三维雷诺时均N-S方程来描述泵站内不可压缩流体的湍流流动。湍流模型采用标准k-ε模型。标准k-ε模型通过修正湍流黏度考虑了平均流动中的旋转及旋转流动情况,可以更好地处理高应变率及流线弯曲程度大的流动。
2.2 动静交界面
对于泵站来说,包含旋转的叶轮、静止的导叶和进、出水池,其中进水池与叶轮、叶轮与导叶之间有相互流动耦合作用,处理动静交界面对整个装置的计算起重要影响。本文采用多参考系模型处理动静交界面,以保证交界面的连续性。
2.3 边界条件及网格剖分
进口条件采用的是质量入口,给定进口边界上的质量流量。出口边界取在出水流道较远处,由于出流边界上的压力或速度均未知,故采用自由出流。在固体边壁处规定无滑移条件(即u=v=w=0),在近壁区的流速分布按照壁面定律确定。
部分采用结构化网格划分,由于叶轮及导叶等部分,几何形状复杂,采用非结构化网格进行剖分,局部加密网格,并完成网格无关性验证,计算总网格数为190万。其中进水池网格数量60万,叶轮21万,导叶49万,出水池60万。对进水池部分进行20~80万数量网格无关性验算,叶轮部分进行10~50万数量网格无关性验算。分别采用效率以及扬程作为评判指标,图3表明,当进水池网格数达到50万以后,再增加网格数对效率影响不是很大。当叶轮部分网格数量达到20万后,泵段扬程在2.372附近浮动,扬程变化较小。最终从占用计算资源的角度考虑,最终选取进水池60万、叶轮21万网格单元数进行计算。
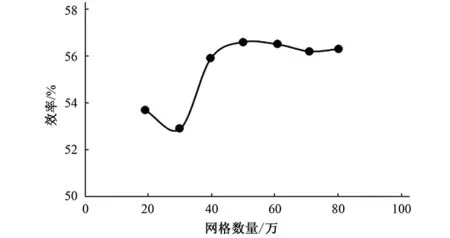
图3 网格无关性验证
3 数值模拟结果与分析
3.1 导水锥
为消除进水池底部可能产生的附底涡以及研究导水锥形式对泵站水力性能影响,共设计了9种方案(包括未加导水锥方案)。表1为导水锥形式优化方案。HZ为导水锥高度,BZ为导水锥底宽。

表1 导水锥形式优化方案
3.2 三角形导水锥高度
表2为不同三角形导水锥高度下效率比较,图4为进水池内部轴向压力分布图。由表2可知,随着三角形高度的增加,泵站水力性能下降,表明过高的导水锥在一定程度上阻碍了进水池向喇叭管的进水,影响了喇叭管下方水流的绕流。几个方案的流线相对比较均匀。对比方案4与方案2,水力性能相差较小,效率变幅为0.27%,与未加导水锥相比,变幅下降了0.34%。方案2与方案1相比,效率下降0.07%。图4表明:在喇叭管处,沿着水流流向压力均匀递增,无负压形成。从消除进水池下方附底涡产生的条件的角度,如果采用三角形导水锥,推荐采用方案2。

表2 三角形导水锥水力性能比较

图4 进水池内部轴向压力分布图
3.3 三角形导水锥底宽
表3为不同三角形导水锥底宽效率比较,图5为进水池出口断面压力分布。由表3可知,随着三角形导水锥底宽的增加,泵站水力性能增强,效率有所提高,变幅达到0.38%。底宽过小,在喇叭管后下方因过大空间易形成滞留区,影响水泵效率。图5各方案压力面上的轴向流速矢量分布均匀,均由高压指向低压,定量计算流速均匀度分别为0.86,0.82,0.87。如果采用三角形导水锥,推荐采用方案2。

表3 三角形导水锥水力性能比较

图5 出口断面压力分布图
3.4 传统型导水锥
表4为传统型导水锥在不同底宽下的效率比较,随着底宽的增加,泵站水力性能下降,表明导水锥的底宽过宽,在一定程度上阻碍了进水池向喇叭管的进水。对比方案9与方案7,水力性能相差较小,效率下降了0.25%,与原方案(方案1)相比,效率下降了0.21%。方案7与方案1相比,效率上升0.04%。图6进水池内部轴向压力分布图表明,导水锥两侧压力分布沿着水流方向均匀递增。从消除进水池下方附底涡产生的条件的角度,如果采用传统型导水锥,推荐采用方案7。
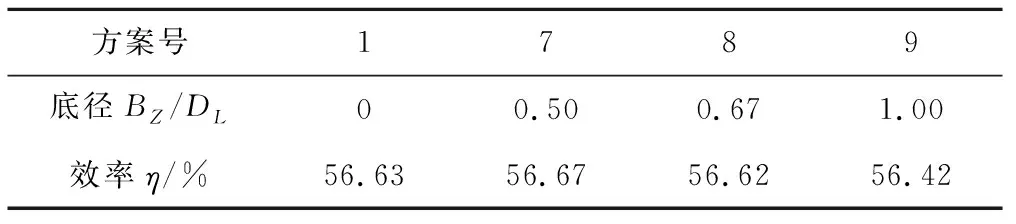
表4 传统型导水锥水力性能比较
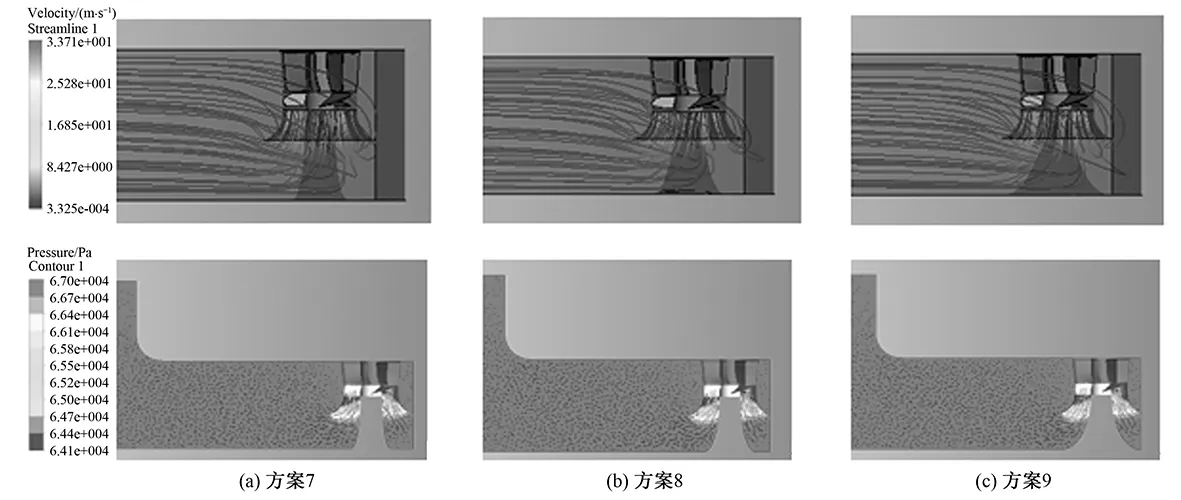
图6 进水池内部轴向压力分布图
4 结 语
三角形导水锥,随着三角形高度的增加,泵站效率在下降,说明过高的导水锥在一定程度上阻碍了进水池向喇叭管的进水。随着三角形底宽的增加,泵站效率在增加,说明增大底宽对喇叭管进水起导流作用。
传统型导水锥,随着底宽的增加,效率在下降,说明过大的底宽不利于喇叭口的进水。
无论是采用三角形导水锥还是传统型导水锥,从效率的角度而言,它们对于泵站效率的影响不是很大。从考虑消涡的角度而言,设置导水锥是很有必要的,将有效减小进水池底部产生的附底涡。

