基于马氏距离判别的丹江口水库长期径流分级预报

程忠良，刘 勇，高 成，胡 健

(1. 河海大学水文水资源学院，南京 210098；2. 南京水利科学研究院 水文水资源与水利工程科学国家重点实验室，南京 210029；3. 中国科学院 陆地水循环及地表过程重点实验室，北京 100101)

0 引 言

径流预报是水文学的重要应用领域之一，也是水库运行调度和防汛、抗旱以及水资源应急调度等的前提[1]。长期径流预报因其预见期较长、预报精度不高，难以满足人们对社会经济生产安排的需求，一直以来都是水文领域研究的难点之一。水文预测方法众多，通常大致可分为过程驱动和数据驱动两大类[2]。其中过程驱动法是基于产汇流机制建立的模型，是径流预测的一个发展方向。但由于径流受到气候气象、下垫面、人类活动等多方面不确定性因素的影响[3]，其形成机理和规律尚未被完全掌握，预报精度不高，使得该方法的应用十分困难。随着数据获取能力和计算能力的发展，数据驱动模型在水文预报中的应用也愈加广泛，神经网络[4]、支持向量机[5]等预测方法在实际应用中也取得了一定的成果。近年来，通过发掘未来径流与前期降雨、海表温度、大气环流指数等大尺度气候-水文变量间的关联关系，建立基于物理成因背景的径流预报模型是目前研究的重要方向[6-9]。冯小冲[6]、刘勇[7]等通过对影响丹江口水库入库径流的气候和水文气象物理因子的分析，筛选出与径流密切相关的物理因子作为预报因子，分别采用逐步回归和神经网络的方法构建月径流预报模型，取得了一定的成果。在气候变化和高强度人类活动的背景下，全球海洋和大气环流均发生了显著的年代际变化[10]，水库来水量的变化也随之加剧，单独采用定性或定量的回归预报模型存在预报误差偏大和精度偏低的问题。为进一步提高预报的精度和可靠性，本文拟在前人研究的基础上，采用定性定量相结合的预报方法，从影响丹江口水库长期径流的物理成因出发选择预报因子，采用AIC准则筛选关键因子，划分径流级别，利用马氏距离判别分析的分类判别优势，构建长期径流分级预报模型，并与逐步回归模型作比较。

1 研究思路及方法

1.1 研究思路

首先从物理成因出发，考虑影响丹江口水库入库径流的海温、环流等因素，采用单相关系数法，计算预报因子与预报径流之间的相关系数r，并作0.05信度水平下的检验，初选出基础预报因子集。然后，将资料序列划分为模拟期和检验期，模拟期的径流按照距平要素值划分为丰、平、枯三个级别，采用AIC准则进一步筛选出关键因子集，构建分段多元线性回归方程，对预报对象进行模拟；检验期时，采用马氏距离判别法根据预报因子对预报径流先做出定性判别，再依据定性判别类别代入相应的线性回归方程，做出定量预报，并将该预报模型与逐步回归模型的模拟和预报结果进行对比，从预报精度和稳定性两个方面去比较两种模型。

1.2 研究方法

1.2.1 单相关系数法

在水文中长期预测中常采用相关系数来考察预报因子与预报对象之间是否线性相关，并以此作为因子挑选的依据[3]。单相关系数的公式为：

(1)

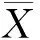
1.2.2 AIC准则

因子个数p的选取对模型的预报精度和稳定性具有很大的影响。取较小的p，拟合程度较差；取较大的p，则受偶然变化影响太大，甚至出现过度拟合的现象，预报效果会受到影响。AIC是衡量统计模型拟合优良性的一种标准，由日本统计学家赤池弘次在1974年提出，它建立在熵的概念上，提供了权衡估计模型复杂度和拟合数据优良性的标准。现定义一个准则函数为：

(2)

式中：σ2(p)为误差的方差；p为因子个数；n为样本个数。

其中第一项代表的是拟合优度，第二项代表了增加因子后的惩罚，权衡两者，选取最小的AIC(p)作为合理的因子个数p。利用AIC准则筛选出关键预报因子集，用于建立回归方程。

1.2.3 马氏距离判别分析

马氏距离是由印度统计学家马哈拉诺比斯(Mahalanobis)提出的，表示数据的协方差距离。马氏距离判别分析法是根据观测到的样本的若干数量特征对新获得的样本进行归类、识别，判别其所属类型的一种有效计算样本集相似度的统计分析方法。相比于欧氏距离判别方法，马氏距离的优势在于不受量纲的影响，两点间的马氏距离与原始数据的测量无关，可排除变量间相关性的干扰。该方法的主要思想是比较样本到各个总体的马氏距离，然后将其判给马氏距离最近的那个总体。

设有k个m维总体G1，G2，…，Gk，均值向量分别为μ1，μ2，…，μk，协方差矩阵分别为∑1，∑2，…，∑k，则样本X到各组的马氏距离为：

D2(X,Gα)=(X-μα)T∑α-1(X-μα)

(3)

α=1，2，…，k

判别规则为：若D2(X，Gi)=min1≤α≤kD2(X，Gα)则X∈Gi。

针对实际问题，当μ1，μ2，…，μk和∑1，∑2，…，∑k均未知时，可以通过相应的样本估计值来替代，马氏距离的具体计算步骤如下。

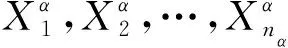
(4)

(5)

(6)

采用马氏距离判别法，计算样本到各个总体的马氏距离，利用马氏距离最小准则对预报期径流的丰、平、枯类别做出定性预报。

1.2.4 多元线性回归

多元线性回归是用于研究一个随机变量和多个变量之间相关关系的方法，利用多个因子X1，X2，…，Xm与对象Y建立多元回归方程：

Y=b0+b1X1+b2X2+…+bmXm

(7)

其中b0，b1，…，bm为回归系数，多元线性回归方程的回归系数采用最小二乘法来确定。根据预报因子和预报对象之间的关系可以建立相应的回归方程，做出定量预报。

1.3 模型精度评定方法

模型的精度和稳定性采用《水文情报预报规范》(GB/T22482-2008)[11]中的确定性系数和平均绝对误差来评定，确定性系数DC和平均绝对误差e的计算公式见式(8)和式(9)。

(8)

(9)

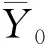
2 丹江口9月入库径流预报

2.1 研究区域概况

丹江口水库位于汉江中上游，丹江与汉江干流汇合以下800 m处，其地理位置处于东经106°12′～111°26′，北纬31°24′～34°11′之间，是南水北调中线工程的水源地。汉江丹江口水库具有防洪、发电、灌溉、航运和养殖等五大功能，水库多年平均入库水量为394.8 亿m3，控制流域面积95 217 km2,是我国大型综合利用水库之一。

2.2 预报因子初选

利用收集到的丹江口水库1952-2008年的9月入库径流资料以及北太平洋逐月平均海温、北半球100 hPa和500 hPa逐月平均高度场以及74项逐月环流特征量资料，分别对各要素场的因子进行相关性普查，并通过0.05的显著性检验。初步筛选出北半球100 hPa逐月平均高度场因子5项、北半球500 hPa逐月平均高度场因子7项、北太平洋海温场因子5项、74项环流特征量因子6项，建立径流预报基础因子集。

2.3 基于马氏距离判别分析的长期径流分级预报

把丹江口水库1952-2008年9月入库径流量资料分为模拟期(1952-2000年)和检验期(2001-2008年)，并根据《水文情报预报规范》(GB/T22482-2008)[11]，将丹江口水库模拟期的9月入库径流按照距平值划分为丰、平、枯三段，详细划分标准见表1。

表1 丰、平、枯级别划分标准Tab.1 standard of division of high, flat and dry

采用AIC准则进行关键预报因子的遴选。筛选出的关键因子集见表2。

从筛选的因子集来看，预报因子对于不同径流级别的预报影响存在差异，海温因子对偏丰径流的预报影响较大，而100 hPa和500 hPa位势高度对偏枯径流的预报影响较大，未发现对丰、平、枯均有良好预报影响的因子。

表2 AIC准则筛选的关键因子集Tab.2 key factor sets selected by AIC

根据AIC准则筛选出的关键影响因子，利用多元线性回归法，建立的分段线性回归方程如下：

(10)

根据建立的回归方程，可对模拟期1952-2000年的9月入库径流进行模拟预报。

根据筛选出的关键因子集，利用马氏距离判别法进行判别分析，判别分析结果见表3。

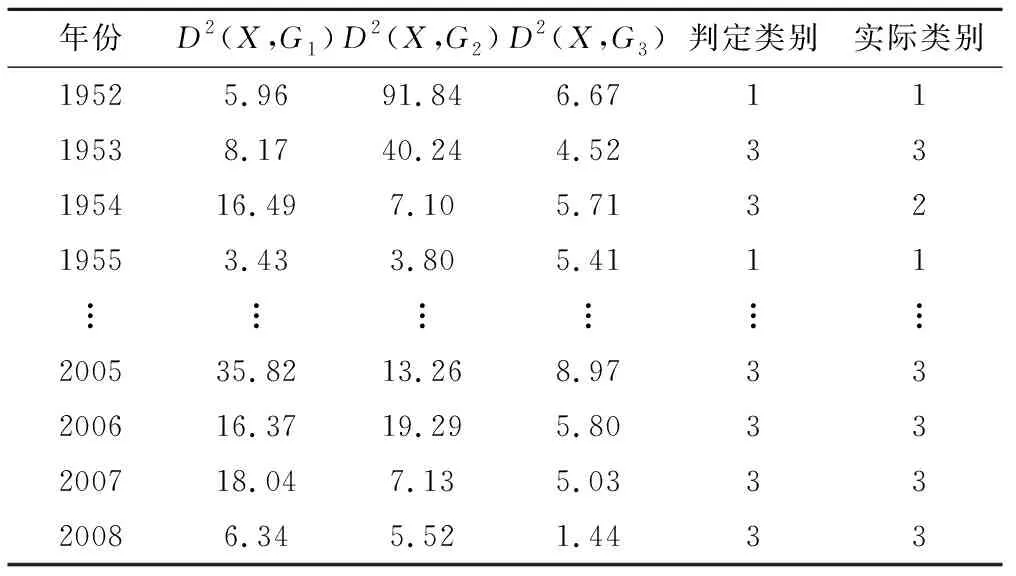
表3 马氏距离判别计算表Tab.3 Mahalanobis distance discriminate calculation table

训练期1952-2000年的49年中有43年判定合格，合格率为87.8%；检验期2001-2008年的8年中有7年判定合格，合格率为87.5%，具有较高精度。对于检验期2001-2008年，根据马氏距离判别分析的类别，代入相应的回归方程，做出预报。

2.4 逐步回归法预报模型

根据预报初选因子集，采用逐步回归分析的方法进一步筛选和确定关键影响因子集，筛选出的关键影响因子集见表4。

利用筛选出的关键因子集构建回归方程，预报方程见式(11)。

Y=99.96+0.206X1-0.180X2-0.142X3-0.397X4+

20.1X5+3.60X6+0.799X7+ 5.03X8-6.70X9-2.23X10

(11)

3 预报成果对比分析

利用基于马氏距离判别的长期径流预报模型(方法1)和逐步回归预报模型(方法2)分别对丹江口水库9月入库径流量进行模拟预报，模拟期预报成果见图1。

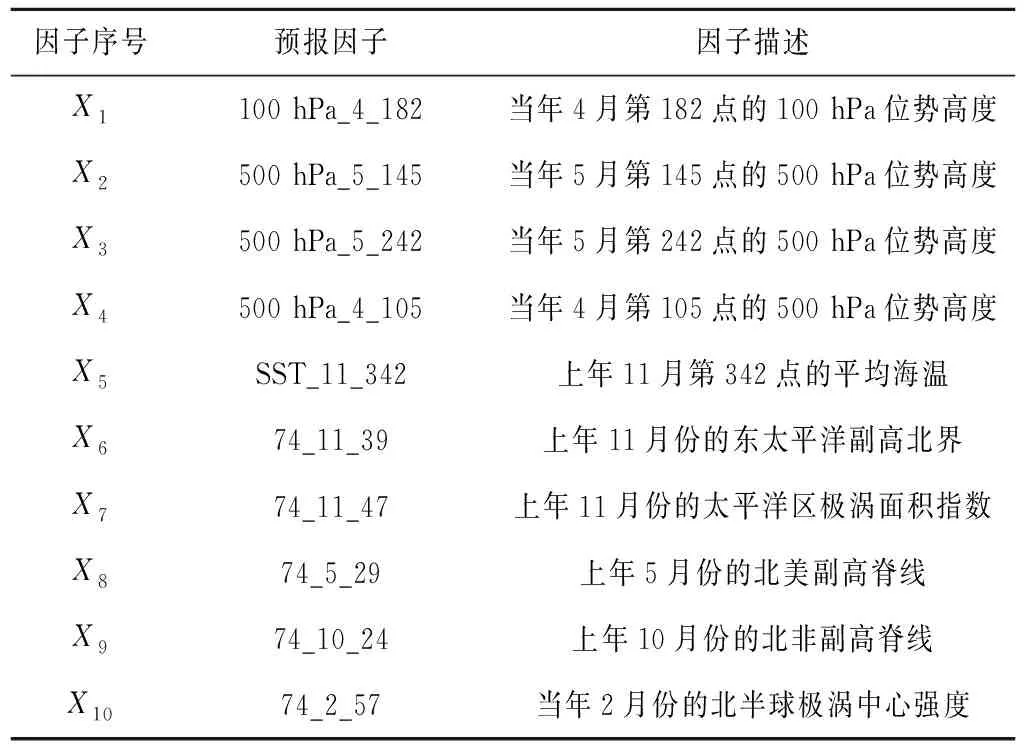
表4 逐步回归分析筛选的关键因子集Tab.4 key factor sets selected by stepwise regression analysis

图1 丹江口水库9月入库径流量实测值与模拟值Fig.1 The measured value and simulated value of the Danjiangkou reservoir in September

从模拟结果来看，根据《水文情报预报规范》(GB/T22482-2008)[11]中评定中长期预报精度的方案作为预报精度模型预报的评价标准：对于定量预报，水位(流量)按多年变幅的10%、其他要素按20%，要素极值的出现时间按多年变幅的30%作为许可误差。采用多年变幅的10%(22.73 亿m3)作为许可误差，方法1的49年模拟期中有46年满足要求，合格率为93.8%，方法2的49年模拟期中有44年满足要求，合格率为89.8%。两种方法的确定性系数DC和平均绝对误差e见表5。

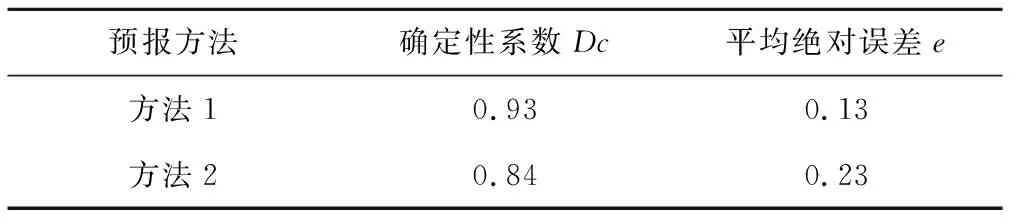
表5 模型确定性系数和平均绝对误差统计表Tab.5 statistical table of deterministic coefficientand mean absolute error

在检验期2001-2008年的8年中，两种方法的实测值与预报值的误差见表6。

根据多年变幅的10%作为许可误差，方法1中只有2003年的预报误差超过允许值，预报的合格率为87.5%；方法2中的2003年和2007年的误差超过允许值，合格率为75%。

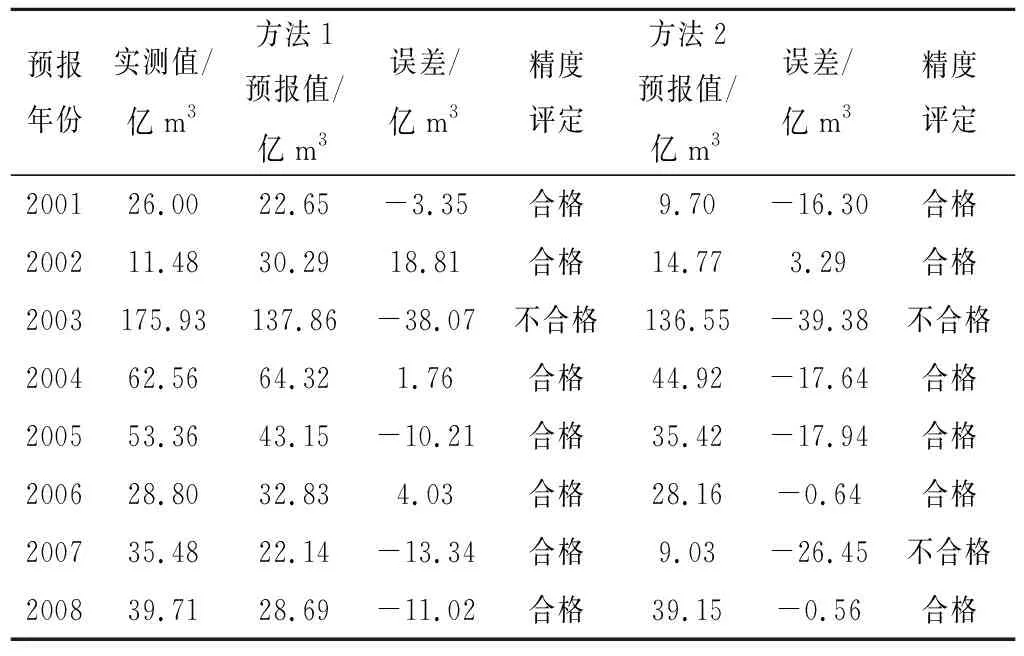
表6 检验期实测值与预报值误差统计表Tab.6 statistical table of measured and predictedvalues in the test period

4 结 语

(1)预报结果表明，基于马氏距离判别的分级预报模型采用定性定量预报相结合的方法，预报的精度和稳定性优于采用单一定量预报的逐步回归模型。

(2)利用AIC准则通过综合考虑模型精度和复杂度来确定因子个数，对于提高预报精度和稳定性有一定的帮助，提高预报精度关键在于提高因子的代表性而不仅仅是增加因子的数量。

(3)基于物理成因出发筛选出的预报因子对提高预报精度有较好的效果，今后可加强预报因子之间的关联性分析以及预报因子与预报对象之间的成因机理分析研究，进一步提高预报因子的相关性和代表性，从而减小预报的误差。