基于分数阶缓冲算子的时变参数离散灰色模型

刘基伟，张辉

(中国传媒大学 理学院，北京 100024)

1 引言

由于对可靠小样本统计的需求日益增长，小样本预测是一个很重要的课题。多年来，学者们对小样本非平稳时间序列的预测问题做了深入研究，突出问题是，对于非平稳时间序列，当系统受到干扰的严重影响时，过去的可用数据不能如实反映系统的规律。因此，为使预测模型的扰动界变小，引入分数阶经典弱化缓冲算子，对原始序列进行微调来提高预测精度，并且通过建立时变参数离散灰色模型对实例进行研究验证。

2 分数阶弱化缓冲算子的构造

经典弱化缓冲算子充分考虑每个数据的优先性，而变权弱化缓冲算子只考虑最新一个数据的优先性[1]，所以从综合利用原有数据信息的角度考虑，经典弱化缓冲算子是一种不错的缓冲算子。

容易证明，经典弱化缓冲算子的阶数越高，越能体现新信息的作用，提高预测质量[1]。但是经典弱化缓冲算子不能实现缓冲作用强度的微调，本文引入分数阶弱化缓冲算子。

一阶弱化缓冲算子的矩阵形式为：

二阶弱化缓冲算子的矩阵形式为

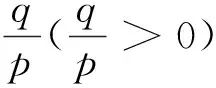
若X(0)为单调衰减序列，因为A(X(0))T≤(X(0))T，A为可逆矩阵，可得A-1A(X(0))T≤A-1(X(0))T，即(X(0))T≤A-1(X(0))T，所以D-1为单调衰减序列的强化缓冲算子；同理D-1为单调增长序列的强化缓冲算子。

若X(0)为震荡序列，x(0)(l)=max{x(0)(k)，k=1，2，…n}，x(0)(h)=min{x(0)(k)，k=1，2，…n}，

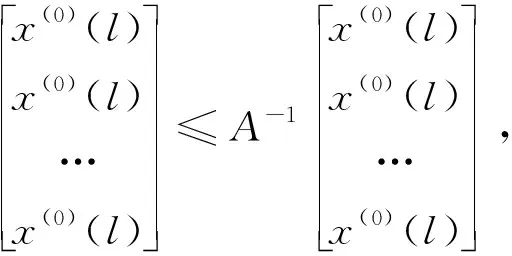
3 时变离散参数灰色预测模型介绍

对于实际应用的数据，因为受到外界诸多冲击因素的干扰而失真。为了能够准确地挖掘事物规律，针对以往模型使用连续时间响应时进行预测产生的跳跃性误差，本文构造二次时变参数离散灰色模型。

定理3.1 设x(0)(k+1)d1=(β1+β2k)x(0)(k)d1+β3k+β4为线性时变参数离散灰色模型，其中x(0)(k)为原始序列观测值，d1为经典弱化缓冲算子。则该模型的最小二乘参数估计分别为：

4 实例研究：不同分数阶预测结果比较

本文以我国北京市科普专项经费为例，比较不同阶数经典弱化缓冲算子对模型预测结果的影响。原始数据见表1，数据来源《中国统计年鉴》。

表1 2008-2015年 江苏省年度科普经费筹集额(万元)

取2008-2014年数据为原始序列，分别建立0.6阶、0.8阶、1阶经典弱化缓冲算子的线性时变参数离散模型，对2015年数据进行预测，预测结果及误差见表2。

表2 三种模型预测值与误差比较

由表2结果对比说明，0.8阶经典弱化缓冲算子可以实现模型的微调，拟精度较高，能较好地挖掘系统的发展趋势，得到比较好的预测精度。