固定翼无人机轨迹跟踪的滑模变结构控制
唐余, 林达
(四川理工学院a.自动化与信息工程学院;b.物理与电子信息工程学院, 四川自贡643000)
引言
在当今社会的各个领域中,无人机已得到了广泛的应用,并将完成更多的任务,比如监视一些危险区域,完成指定任务,其中轨迹跟踪[1]是其基本技能。固定翼无人机因其强悍的长航时和远程工作能力已成为各国军方重点发展的装备。固定翼无人机因为经常高空作业,经常受到风场干扰的影响,并且无人机建模存在不确定性,这两种情况都会导致动力学模型参数发生改变[2-3],所以需要一种具有较强鲁棒性[4]的算法来抵抗这些影响。
目前,针对固定翼无人机的控制问题已经提出了很多方法。其中,文献[5]提出的线性变参数(LPV)方法需要将非线性系统转化为线性系统,再通过配置极点构造反馈控制器,虽然其控制器设计简单且控制效率较高,但在工程应用上难以实现,因为很难在实物上对模型进行线性化处理;文献[6-7]提到的比例积分微分(PID)方法和反步方法虽然控制效果良好且不需要将非线性系统转化为线性系统,但为了获得良好的控制效果,PID方法主要是通过构造一个由误差、误差导数和误差积分组成的稳定闭环回路,所以需要不断调整以获得合适的控制参数,反步法在构造出控制器前需要定义虚拟控制量,这增加了控制参数的数目,也增加了获得合适控制参数的难度。考虑到既不需要改变系统结构,又不需要特意调整控制参数,本文采用滑模变结构[8](SMVSC)方法,不仅其控制参数数量较少,且无人机的控制参数可以通过计算获得。
1固定翼无人机的动力学模型
将飞机视为一个刚体,其在空间中的运动具有六个自由度,包括质心的3个自由度和绕质心旋转的3个自由度,分别是速度的增减、上下升降、左右侧移和俯仰、滚转、偏航运动。飞机的运动主要是受推力和几个飞机操纵面控制,如图1所示。其中发动机产生推力,副翼产生滚转力矩L,取下偏为正向,L值为负;升降翼产生俯仰力矩M,取下偏方向为正向,M值为负;方向翼产生偏航力矩N,取左偏方向为正向,N值为负。考虑速度分量用(u,v,w)表示,无人机姿态分量用(φ,θ,ψ)表示,无人机角速度分量用(p,q,r)表示,以及攻角为α,迎角为β,风速为Va。
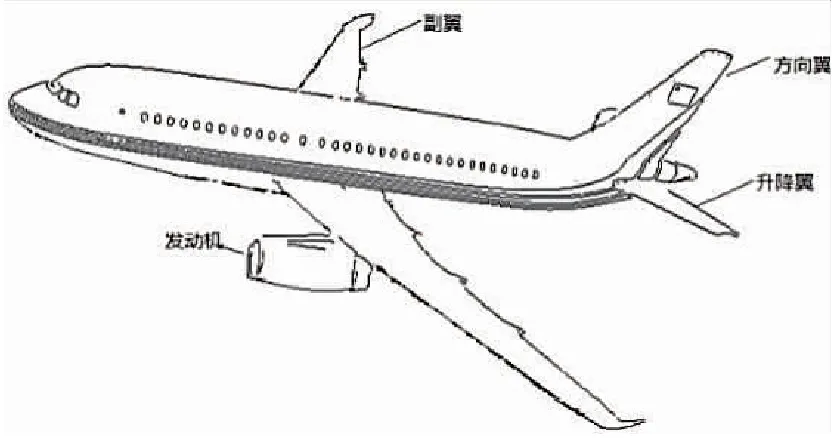
图1固定翼飞机机操纵面
根据文献[9-11],得到带不确定性参数的无人机动力学模型:
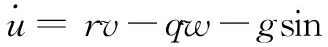
(1)
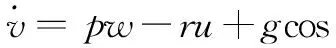
(2)
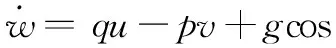
(3)
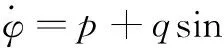
(4)
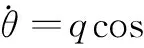
(5)
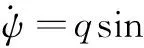
(6)
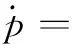
(7)
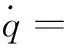
(8)
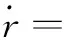
(9)
式中:g是重力加速度,m是无人机质量,Ax,Ay,Az是无人机气动力(阻力、侧向力、气动力),J是发动机推力。L、M、N分别是滚转、俯仰、偏航的力矩,d(t)是模型不确定性参数,Fw是阵风。τi,τ2,τ5,τ6,τ7由惯性常量Jx、Jy、Jz、Jxz相互组合计算而得,计算过程如下:
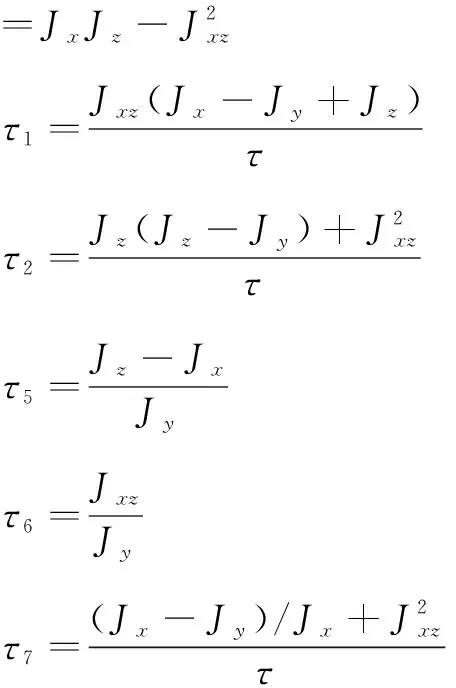
此外,动力学公式中的相应系数为:
(10)
(11)
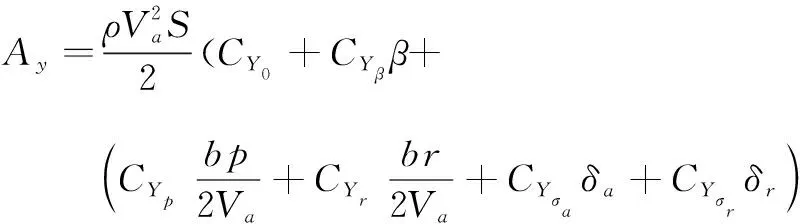
(12)
(13)
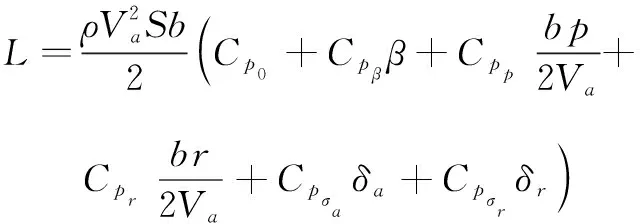
(14)
(15)
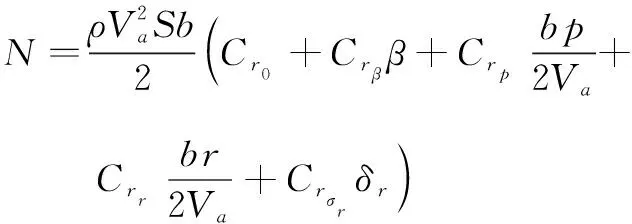
(16)
式中:ρ是空气密度,Sprop是螺旋桨面积,km是电动机效益常数,Cprop是推进器气动系数,S是机翼面积,b是翼展,Va是空速,α是攻角,β是侧滑角,c是机翼平均气动弦,CX(α)、CXq(α)、CXσe(α)是阻力系数,CY0、CYβ、CYp、CYr、CYσa是侧向力系数,CZ(α)、CZq(α)、CZσe(α)是升力系数,Cp0、Cpβ、Cpp、Cpr、Cpσa、Cpσr是滚转力距系数,Cm0、Cma、Cmq、Cmσe是俯仰力矩系数,Cr0、Crβ、Crp、Crr、Crσr是偏航力矩系数,其中δa是无人机副翼控制信号,δe是无人机升降翼控制信号,δr是无人机方向翼控制信号,δt是无人机发动机控制信号。并且:
(17)
α=arctan(w/u)
(18)
β=arcsin(v/Va)
(19)
CX(α)=-CD(α)cosα+CL(α)sinα
(20)
CXq(α)=-CDqcosα+CLqsinα
(21)
CXσe(α)=-CDσecosα+CLσesinα
(22)
CZ(α)=-CD(α)sinα-CL(α)cosα
(23)
CZq(α)=-CDqsinα-CLqcosα
(24)
CZσe(α)=-CDσesinα-CLσecosα
(25)
其中:
CL(α)=CL0+CLaα
CD(a)=CD0+CDαα
2基于滑模变结构的飞行控制
在实际的飞行控制中,包括对无人机的轨迹和姿态进行控制,因为无人机的轨迹和姿态受控制信号δa、δe、δr、δt影响,所以可以根据式 (1)与式(3)和无人机的参考轨迹设计控制回路,求解出控制信号δe、δt,再根据式(6)与式(9)和无人机期望的偏航角ψd设计出偏航角控制回路,求解出δr,再联合式(2)求解出δa。
2.1控制策略
固定翼无人机是一个欠驱动、强耦合的系统,本文采用的控制策略如图2所示。
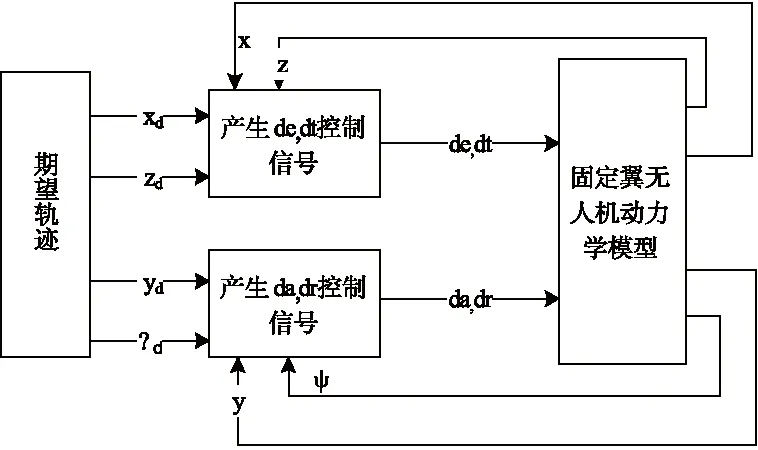
图2固定翼无人机控制策略
2.2固定翼无人机控制信号δe、δt求解
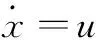
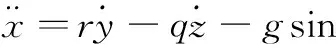
(26)
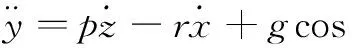
(27)
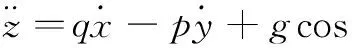
(28)
假设无人机的参考轨迹为xd、yd、zd,令:
ex=x-xd
(29)
ey=y-yd
(30)
ez=z-zd
(31)
根据文献[12-14],设计跟踪滑模函数:
(32)
(33)
(34)
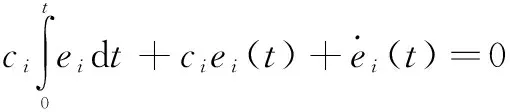
定义Lyapunov函数:
(35)
从而有
(36)
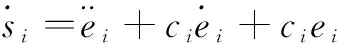
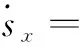
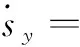

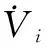
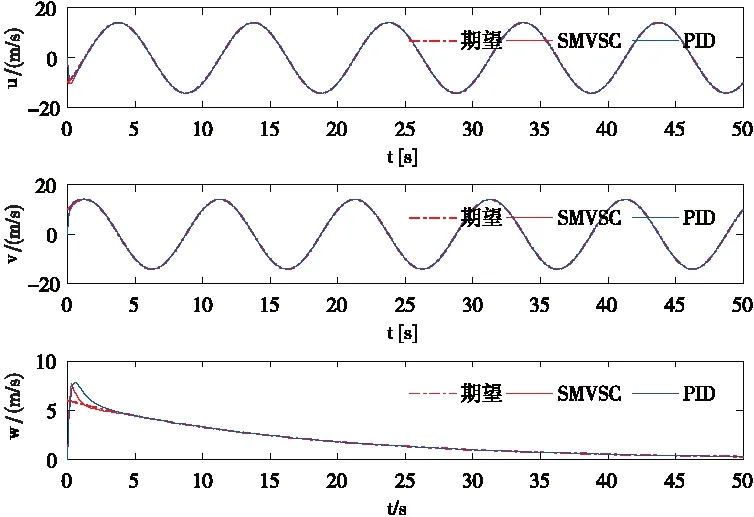
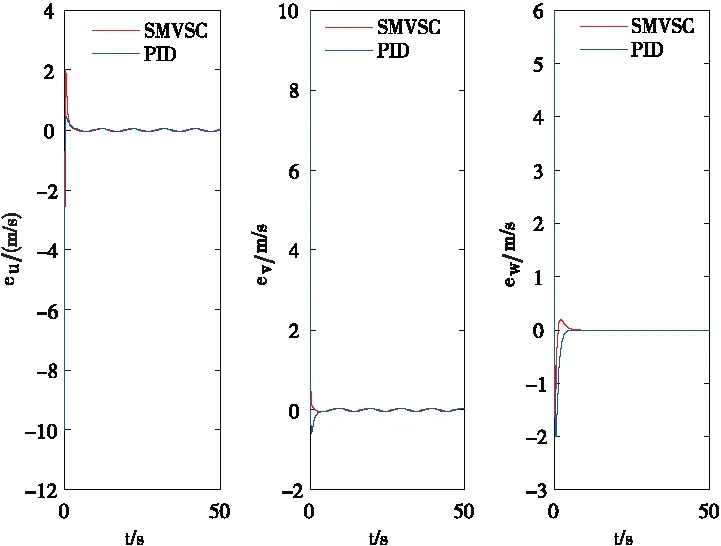
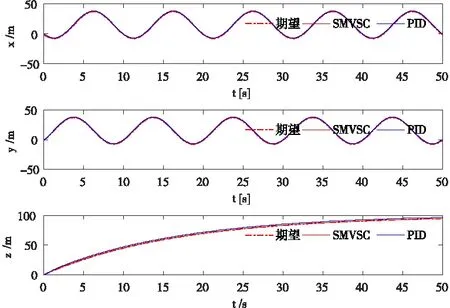
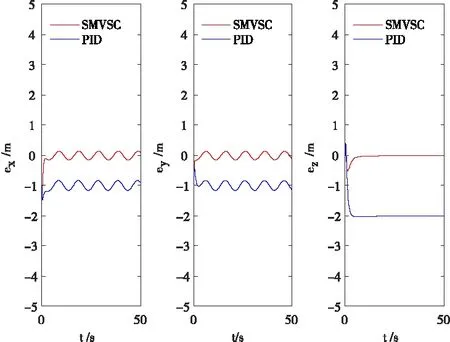
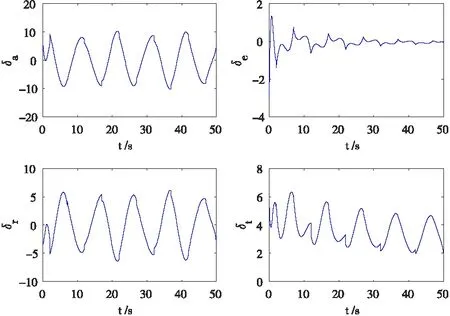
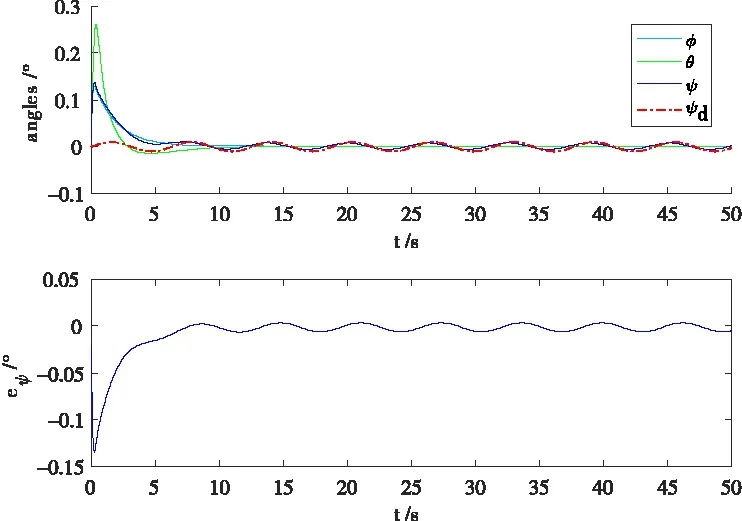
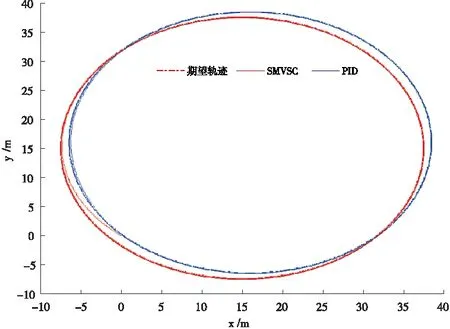
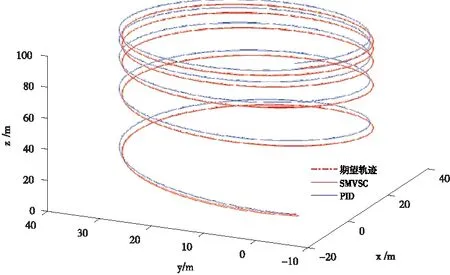
Vi(t) Ax+J=m(-kxsx-sat (sx)- (37) Ay=m(-kysy-sat (sy)- (38) Az=m(-kzsz-sat (sz)- (39) 将式(37)~式(39)分别代入式(26)~式(28)可得: -kisi-sat (si)-Dsign (si)+ d(t) < -kisi 由上述证明可知si收敛,所以上式能构成一个稳定的闭环回路,保证ei收敛于0。 由式(13)和式(39)可得: (40) 由式(10)、式(11)和式(40)可得: (41) 假设期望偏航角为ψd,则根据式(6)可求得期望角速度rd: 令: er=r-rd 根据2.2的推导过程可得: N=-krs-sat (s)-Dsign (s)+ (42) 将式(42)代入式(9)可得到稳定得闭环系统: Dsign (s) +d(t) < -krs 其中s收敛于0。可得到如下收敛效果: er(t)=er(0)e-crt 其中,er的收敛速度取决于cr值的大小以及s的收敛速度。 由式(16)与式(42)可得: (43) 由式(12)、式(38)和式(43)可得: (44) 本文使用Matlab软件对式(45)表示的期望轨迹进行仿真,PID控制器设计过程参考文献[15],固定翼无人机的物理参数见表1,SMVSC算法仿真参数Ki=4、ci=6(其中i=x,y,z,r),PID算法仿真参数:kp=kd=6,ki=0。为了验证本文控制算法的收敛性以及控制性能,在仿真过程中加入外界阵风干扰为D=[Dx,Dy,Dz]T=[120,120,120]T,即三个方向上的干扰力均为120 N的较强阵风,仿真结果如图3~图11所示。 (45) 图3无人机速度跟踪 图4无人机速度误差 图5无人机位置跟踪 图6无人机位置误差 图7无人机控制输入 图8无人机姿态角,期望偏航角,偏航角控制误 图9无人机空速,攻角和迎角 图10无人机轨迹跟踪(俯视图) 图11无人机轨迹跟踪(三维图) 从图3~图6可知,在无人机速度跟踪方面,采用SMVSC控制算法或PID控制算法达到的稳态误差大致相当,但是相对于PID算法,采用SMVSC算法达到控制效果较为稳定,初始误差更小,能在极短的时间内完成速度跟踪;在无人机位置跟踪方面,PID算法明显就不如SMVSC算法,其稳态误差远大于SMVSC算法。 图7为飞行器四个控制信号的仿真图。图8给为无人机的飞行姿态。图10和图11为无人机轨迹跟踪的俯视图和三维图。从仿真结果来看,应用本文提出的SMVSC算法,无人机飞行更加稳定,轨迹跟踪性能更强。 本文提出的滑模变结构方法,对于结构复杂,MIMO且呈非线性强耦合的固定翼无人机具有良好的控制效果,不但能有效减小稳态误差,而且可以在较强的阵风干扰和不确定参数的影响下不偏离期望轨迹。通过与PID控制方法比较发现,该方法具有较强的鲁棒性和抗干扰能力。在下一步研究中,考虑在滑模控制中引入智能控制算法,这样不仅能完成轨迹跟踪任务,还能进行最优路径规划。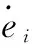
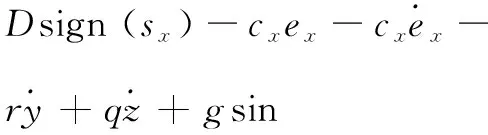
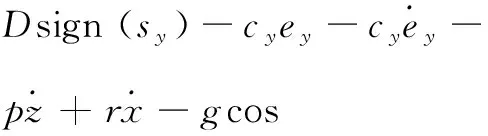
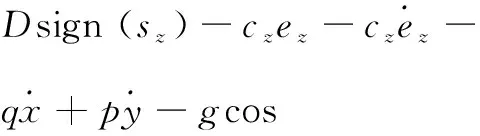
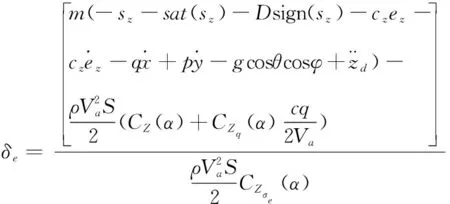
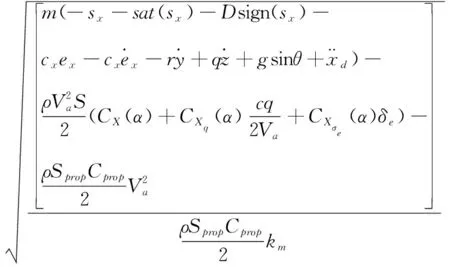
2.3固定翼无人机控制信号δr、δa求解
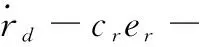
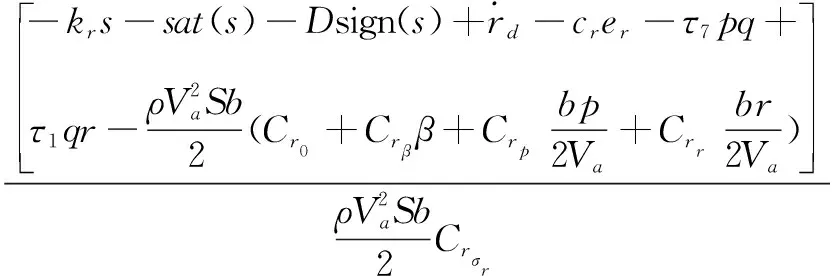
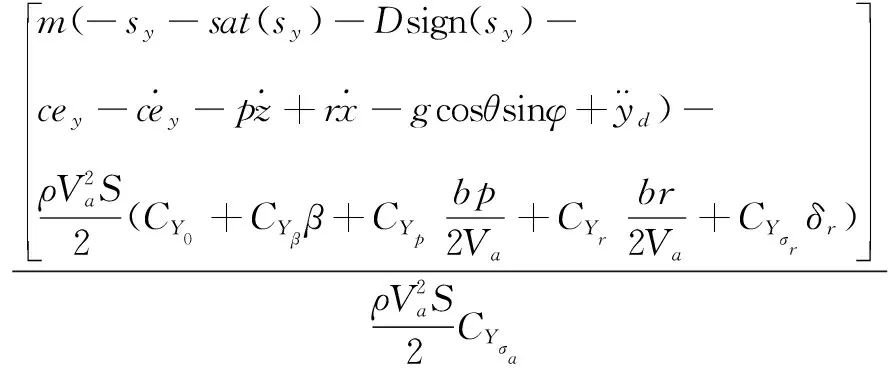
3仿真与分析

4结束语

