曲柄滑块机构滑块匀速运动研究

李昊轩 何恒健 刘浩南 李岳林

(长沙理工大学汽车与机械工程学院，湖南 长沙 410114)

曲柄滑块机构的作用是将曲柄的旋转运动转换成滑块的往复直线运动。因此，在工业生产中得到广泛应用[1-3]，在食品加工、食品包装的机械设备中也承担着重要作用[4-5]。但在原动机匀速转动的情况下，其滑块速度和加速度按类似正弦函数关系随时间变化[6]，限制了曲柄滑块机构在许多方面的应用。在切片、摊铺等工作中，往往要求滑块能够匀速运动。文献[7]以滑块速度波动与平均速度的差值最小为优化目标，用粒子群算法对曲柄滑块机构进行优化设计，在原动机匀速转动的条件下，得到了优化的曲柄长度与连杆长度(均为固定值)，但并未给出滑块实际运动速度曲线。理论上，改变原动机的转速变化规律，可以近似实现滑块匀速运动，但对原动机的转速控制非常困难，需要复杂的控制算法[8-9]，且使得原动机的转速变化非常剧烈。为避免对原动机进行复杂控制，又实现滑块匀速运动，本研究根据曲柄滑块机构的几何关系，用复数矢量法分析得到曲柄长度与位置夹角的解析关系；在此基础上，由滑块匀速运动的期望值，求解该解析关系的差分方程，得到曲柄长度的变化规律，并设计了一种可改变曲柄长度的曲柄滑块机构，通过SolidWorks/Motion仿真验证其可行性。

1 曲柄长度与曲柄位置的关系

如图1所示，设定曲柄的长度L1是随时变化的，且以ω1的角速度匀速转动；连杆的长度L2固定；设计目标是在机构正常工作过程中滑块在水平方向上作匀速运动，即VC为固定速度值[10]。机构的运动分析可采用复数矢量法[11]进行推导解析。

由几何向量关系列出机构的矢量封闭方程：

(1)

矢量封闭方程[式(1)]转换成复数形式，可表示为：

L1eiφ1+L2eiφ2=XC。

(2)

利用欧拉公式展开式(2)得：

A. 表示曲柄与机架连接L1. 曲柄的长度 B. 曲柄与连杆连接L2. 连杆的长度 C. 滑块

图1 曲柄滑块机构简图

Figure 1 Schematic diagram of slider-crank mechanism

L1sinφ1+L2sinφ2=0，

(3)

L1cosφ1+L2cosφ2=XC。

(4)

对式(2)两端关于t求导，得：

(5)

式(5)两边乘上e-iφ2，展开取实部得：

(6)

将式(3)代入式(6)，得：

(7)

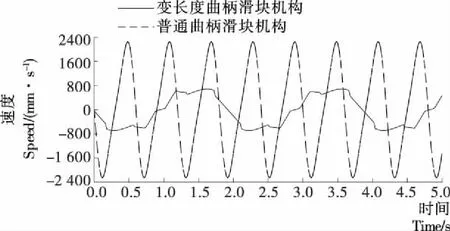
由于cosφ2>0，0

(8)

即：

(9)

(10)

根据曲柄长度与其所处角度的关系设计出通过带凸轮槽以改变曲柄长度的装置，具体结构见图3。设计曲柄滑块机构实现滑块匀速运动时，在曲柄与连杆的连接处设置一个导柱，导柱随着旋转块的旋转在变曲柄长度装置上按照凸轮槽轨迹运行，达到改变曲柄长度的效果，具体结构见图4。

图2 曲柄长度(L1)与曲柄位置(φ1)关系图

图3 变曲柄长度装置结构示意图

1. 变长度装置 2. 曲柄 3. 导柱 4. 连杆 5. 滑块 6. 旋转块

2 变曲柄长度滑块机构运动解析

在对变曲柄长度的曲柄滑块机构进行运动解析时，可选滑块作为研究对象，依据动态静力学理论，得到滑块受力见图5，平衡方程见式(11)。

Fi+F+FN+mg=0，

(11)

式中：

Fi——滑块所受的合力,Fi=-ma,N；

m——滑块质量,kg；

a——滑块加速度,m/s2；

F——连杆施加在滑块上的力,N；

FN——机架施加在滑块上的力,N；

g——重力加速度,m/s2。

图5 滑块受力图

选取直角坐标系Oxy(图1)，将式(5)分别在x、y轴上投影得：

(12)

滑块坐标(x,y)为：

(13)

由几何关系：

L1sinφ1=L2sinφ2。

(14)

化简得：

(15)

由三角函数关系得：

(16)

将式(16)代入式(13)得：

(17)

对时间求导

(18)

同理，再将速度对时间求导得到加速度与时间的关系表达式，在图4所示的带凸轮槽的曲柄滑块机构结构示意图中，假定连杆长度L2=500 mm(该长度值可以根据实际需要选取)；曲柄长度L1按式(10)计算出的数据变化关系而改变；旋转块连接电机输出轴，电机转速为100 r/min。

3 机构动力学分析

通过SolidWorks/Motion软件[12]对变长度曲柄滑块机构与普通滑块机构进行了对比分析。在使用SolidWorks/Motion软件时，首先需要创建零部件、设置零部件的配合关系、设置驱动、软件对机构进行动力学计算、生成数据图表。普通曲柄滑块机构与变长度曲柄滑块机构的参数设置见表1。

变长度曲柄滑块机构与普通滑块机构的滑块速度和加速度对比分别见图6、7。图6中的曲线表明，变长度曲柄滑块机构在除滑块转换方向以外(即工作行程中)基本保持在800 mm/s 的速度。而且换向时间较短，约为0.2 s。图7表明，变长度曲柄滑块机构的加速度变化频率更高，加速度变化的作用是对滑块运行速度进行调整，从而实现滑块匀速运动。

表1 普通曲柄滑块机构与变长度曲柄滑块机构的参数对比

Table 1 Comparison of the parameters between crank-slider mechanism and variable length crank-slider mechanism

机构曲柄长度/mm连杆长度/mm电机转速/(r·min-1)普通曲柄滑块机构 200500100变长度曲柄滑块机构式(10)计算结果500100

图6 不同机构中滑块速度时间关系对比图

图7 不同机构中滑块加速度时间关系对比图

驱动电机的力矩对比见图8，能源消耗见图9。图8与图9表明,普通曲柄滑块机构在滑块运行方向改变时，驱动电机的力矩急剧增大，对机构造成较大的冲击。而变长度曲柄滑块机构力矩平缓，且能源消耗相对较低。

图8 电机力矩对比图

Figure 8 Diagram of motor torque in crank-slider mechanism and variable length crank-slider mechanism

图9 能源消耗对比图

Figure 9 Diagram of energy consumption in crank-slider mechanism and variable length crank-slider mechanism

4 结论

(1) 原动机匀速运行时，滑块运行速度严重不均匀是曲柄滑块机构的固有特点，本研究提出了一种曲柄滑块机构中滑块匀速运动的实现方法，与普通曲柄滑块机构的仿真结果对比表明：在普通曲柄滑块机构中增加改变曲柄长度的装置，能够较好地实现滑块在每个工作行程中同一运动方向的匀速运动。

(2) 由于滑块速度均匀性的改善，其加速度均匀性也得到很好的改善，从而有效降低了原动机的力矩突变，能源消耗明显降低。

(3) 该方法可推广至其他四杆机构以及复杂机构中。