动量-自适应学习BP算法在加工领域的探索

耿胜财，胡玉兰

(沈阳理工大学 信息科学与工程学院，沈阳 110159)

在人工智能[1]如火如荼的今天，复杂的事情完全可以交给机器处理。BP(Back Propagation)神经网络[2]，即多层前馈神经网络，是机器学习(Machine Learning,简称ML)中典型学习算法之一，已在函数逼近、模式识别、分类以及数据压缩等方面广泛应用[3-4]。经典的BP算法通常存在学习效率低、收敛速度慢、易陷入局部极小状态等问题。针对以上问题，国内外研究学者常用三种方式对BP算法进行改进：附加动量法、自适应学习速率以及动量-自适应速率调整算法。第三种方式是前两种方式的结合，在缩短训练时间的同时，可以找到全局最优解。目前，国内外关于动量-自适应学习BP算法[5]的应用并没有统一的标准，即对权值或阈值更新时采用何种关于动量法和自适应学习速率的组合，是针对具体问题，通过调参决定的。

本文的研究基于电解加工[6]，电解加工过程非常复杂。通过动量-自适应学习BP算法，建立BP神经网络在电解加工领域的预测模型。该模型利用函数逼近原理，将复杂的电解加工过程装入“黑盒子”，可通过输入加工参数得到输出参数，通过对比输出参数和加工指标得到满足加工要求的参数。

1 影响电解加工的主要因素

电解加工是一种基于金属阳极电化学溶解原理、利用成型的阴极工具将工件加工成型的方法。电参数、电解液参数、工件特征和阴极等参数(如图1所示)为主要影响加工质量的因素。

图1 主要加工参数

用容易测得并容易控制改变的电流值I、电解电压U、脉冲电源频率f、脉冲电源占空比c、初始加工间隙d和电极给进速度v等加工参数进行预测模型研究。

2 BP神经网络模型设计

2.1 BP网络结构的设计

采用单隐含层的BP神经网络，来建立加工参数与加工微孔孔径大小关系的预测模型。BP网络的输入层节点数m=6，分别对应上面提到的6个加工参数；输出层的节点数n=3，分别对应微孔上表面孔径D1(mm)、微孔下表面孔径D2(mm)和电解加工时间t(s)；ωij为第j个输入层节点到第i个隐含层节点的权值，ωki为第i个隐含层节点到第k个输出层节点的权值，BP神经网络结构图如图2所示。

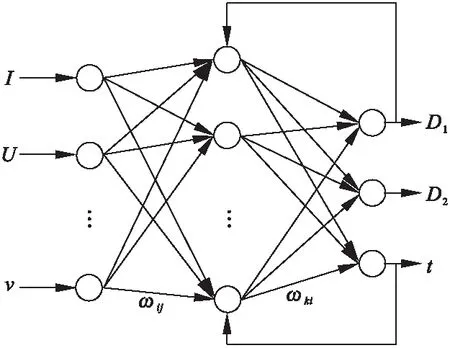
图2 典型三层BP神经网络结构图

BP网络中间隐含层的节点数对网络的学习和计算有重要影响。隐含层节点数过少，网络过于简单不能满足精度要求；隐含层节点数过多，训练时间太长、易出现过拟合以至于泛化能力差。根据经验公式确定隐含层节点数。

(1)

式中，h为隐含层节点个数，b为1～10的任意数。

2.2 动量-自适应学习过程

BP网络的学习过程由前向计算过程和误差反向传播过程组成[5,7]。理论上，至少一个S型隐含层加上一个线性输出的网络，能够逼近任意闭区间的连续函数。因此本文BP网络隐含层传递函数为式(2)，输出层传递函数为式(3)。

y=logsig(x)

(2)

y=x

(3)

式中x、y分别为网络中隐含层和输出层当前节点的总体输入和输出。网络的误差反向传播过程，即首先由输出层计算各层神经元的输出误差，然后根据误差梯度下降法来调节各层的权值和阈值，使修改后的网络最终输出能够接近期望值。系统对P个训练样本的总误差准则函数为式(4)。

(4)

根据误差梯度下降法依次修正输出层权值变化量为Δωki，输出层阈值的变化量为Δa，隐含层权值的变化量为Δωij，隐含层阈值的变化量为Δθi，变化量公式分别如下式：

(5)

(6)

(7)

(8)

式中：η为固定学习速率；xj为第j个输入层节点的输入；yi为第i个隐含层节点的输出。

由于典型的BP算法有学习效率低，收敛速度慢，易陷入局部极小状态，本文将用动量-自适应学习算法将其改进。附加动量法使网络在修正其权值时，不仅考虑误差在梯度上的作用，而且考虑在误差曲面上变化趋势的影响，有利于滑过局部极小值找到全局最小值。自适应学习有利于提高BP神经网络的学习效率，增加其收敛速度，缩短训练时间。改进后各层的权值和阈值的调节公式如下。

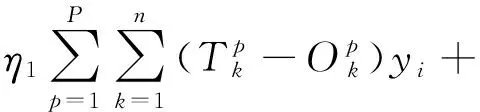
mcΔωki(K)

(9)

(10)

式中：K为训练第K步；mc为动态的动量因子；η1为自适应学习速率。mc和η1调整公式分别为：

mc=mc(1+α)

(11)

(12)

式中：α为动量因子系数，0≤α≤0.5；E(K)为第K步误差平方和；η1(K)为第K步自适应学习速率。

由公式(5)～(12)可以看出，更新阈值时采用自适应学习算法，更新权值时采用动量-自适应学习的算法。

采用批处理的方式进行Matlab仿真，即仅当所有的输入数据都被提交后，网络的权值和阈值才被更新。动量-自适应学习BP算法流程图如图3所示。

图3 BP网络算法程序流程图

3 BP神经网络预测模型与试验验证

3.1 试验装置与设计试验

采用微细加工系统装置的电解部分进行电解加工试验，该系统主要由气体辅助激光加工模块、高频微秒级脉冲电解电源、恒温电解液系统、侧壁绝缘管状电极以及低浓度酸性钝化电解液等模块组成。

试验过程中考虑到成本问题，采用直径0.6mm的裸电极，浓度为8%的NaNO3溶液，电解液恒为21℃，阳极工件0.59mm厚的1Cr18Ni9Ti不锈钢片等。需要试验的6个输入层参数，在有效参数范围内使用正交试验法，既能极大的减少试验次数又能使试验更有代表性和说服力，参数设计见表1。

表1 有效范围内的参数设计

3.2 模型训练与预测结果分析

将表1中的参数用正交试验法设计50组试验，其中40组的试验数据用来训练改进的BP神经网络，剩下的10组数据用以测试训练好的BP神经网络预测模型。训练过程中发现当隐含层的节点个数为10时预测效果最佳，同时确定了改进BP神经网络中各参数的取值。其中，自适应学习速率初使值η0=0.035且0.015≤η1≤0.2，动量因子初始值mc0=0.65且0.65≤mc≤0.9，α=0.001。目标误差E0=4，目标误差过小，会出现过拟合的情况；目标误差过大，会达不到较高的训练拟合度，两者都会大大降低预测精度。加工时间的预测值和试验值的对比如图4所示。

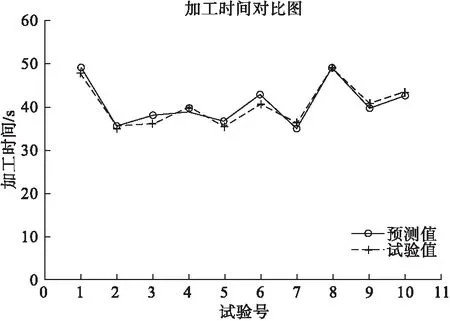
图4 加工时间预测对比

至此，完成一次预测精度的取值。上述过程需重复十次，且每次的分组情况不同，由此得到如表2所示的预测精度误差表。

表2 试验结果的预测精度误差表 %

经计算入口直径模拟误差为5.04%，出口直径模拟误差为4.15%，电解加工时间预测误差为3.29%。其预测误差都在±15%以内，相对于郑旭等[8]在该领域优化工艺参数时得到的平均预测误差5.97%，以及王蕾等[9]在该领域精度预测误差12%有明显的改进效果。预测结果与实际加工结果基本一致，验证了动量-自适应学习BP神经网络电解加工预测模型的有效性。

4 结论

提出用动量-自适应学习BP神经网络对电解加工部分参数预测的模型。选取主要加工参数，确定BP神经网络的模型结构。利用现有的试验系统装置设计了正交试验，用试验结果对动量-自适应学习的BP网络进行训练及测试。经验证，该预测模型对电解加工微孔的出入孔径及加工时间预测精度高达95%。利用机器学习、人工神经网络等智能算法解决实际工程领域中的复杂非线性问题有明显优势，本文的模型对未来的生产具有一定的指导意义。