解凸可行性问题的选择性投影方法

何松年，田瀚琳

（中国民航大学理学院，天津 300300）

1 引言与预备知识

假设H是实Hilbert空间，H的内积和范数分别用〈·，·〉和‖·‖表示。C为定义在H上的有限个凸函数水平集的交集，即其中 m 是一个正整数，ci：H→R（i=1，…，m）是一个凸函数。文中总是假设ci（i=1，…，m）是次可微的且次微分∂ci是有界算子（即在有界集上有界），考虑凸可行性问题即寻找一个点

众所周知，对于H中每一个点x，在C中总存在唯一一个点，记作PCx，满足称PCx为x到C上的度量投影，称PC：x→PCx为H到C的投影算子。

为了求解凸可行问题，在每一步迭代中往往需要计算每个投影PCi，如果这些Ci比较复杂，则计算其非常困难。为克服这一困难，1986年Fukushima[1]介绍了一种方法，即通过计算到包含原始水平集的半空间的一列投影去代替计算到一个凸函数的水平集的投影。之后，此想法被分别应用去解决有限维或无限维Hilbert空间中的分裂可行性问题[2-3]和Hilbert空间中的变分不等式问题[4]。He等[5]应用Fukushima的思想提出了一种松弛的Halpern-type算法[6]用来求解凸可行问题。

算法1∀u∈H取定，取任意一个初始值x0∈H，通过如下迭代格式构造序列{xn}

序列{λn}⊂（0，1）。

对于算法1，He等证明如下结果。

定理 1假设 λn→0（n→∞）和，则由算法 1 产生的序列{xn}强收敛到点

He等的算法可以很好地解决定义在有限个水平集的交集上的凸可行问题。但算法1在每一步迭代中都需计算m次投影，所以算法1的计算量较大。另外，当m较大时，水平集的构造也会越来越复杂。

纵观全文提出一种比算法1更简捷的新算法，称之为选择性投影方法，在新算法每一步迭代中只计算一次投影算子，因而计算量明显减小。

为符号简明起见，将用到如下记号：

2）I表示恒等算子；

为证明主要结果，需用到如下结论。

定义1称算子T：H→H为非扩张的，如果

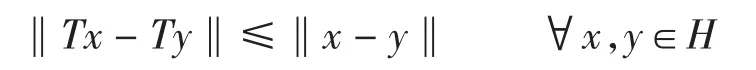
定义2称算子T：H→H是firmly非扩张的，如果

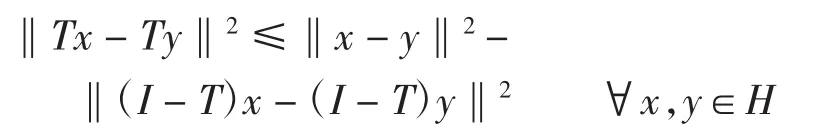
容易验证，算子T：H→H是firmly非扩张的，当且仅当不等式成立，即

众所周知，度量投影算子PC是典型的非扩张算子和firmly非扩张算子。

引理1（钝角原理） 对于x∈H，z∈C，z=PCx的充要条件是

引理2∀x，y∈H，则如下不等式[7]成立

引理3假设{sn}是非负实数列，满足

其中{γn}⊂（0，1），{ηn}是非负实数列且{δn}和{αn}是两实数列，满足：

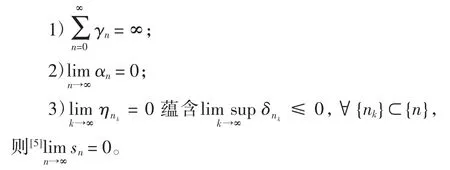
定义3对 f：H→R，若对任何{xn}⊂H，只要，就有

定义4ξ∈H称为f：H→R在点x的一个次梯度，如果满足次微分不等式

如果函数f：H→R在点x至少存在一个次梯度，则称f在点x为次可微的。f在点x的次梯度集用∂f（x）来表示，称为f在x点的次微分。如果f在H中的每一点均次可微，则称函数f次可微。

2 迭代算法

采用选择性投影方法计算PCu，其中u为实Hilbert空间中任意取定的一个向量，C是H中有限个水平集的交集，即其中m是一个正整数，ci：H→R（i=1，…，m）是一个凸函数。

算法2选择性投影算法的步骤：

Step1给定u∈H，任取一初始点x0∈H，且设n=0；

Step2计算并比较c1（xn），c2（xn），…，cm（xn）中的最大值。取 in∈I={1，2，…，m}，使得构造一个半空间

Step3通过如下迭代格式计算xn+1，即

其中 λn∈（0，1）；

Step4令 n=n+1，返回 Step2。

对于算法2，证明了如下强收敛结果。

定理2假设 λn→0（n→∞）和，则由算法 2产生的序列{xn}强收敛到点

证明1）证明{xn}是有界的。令则

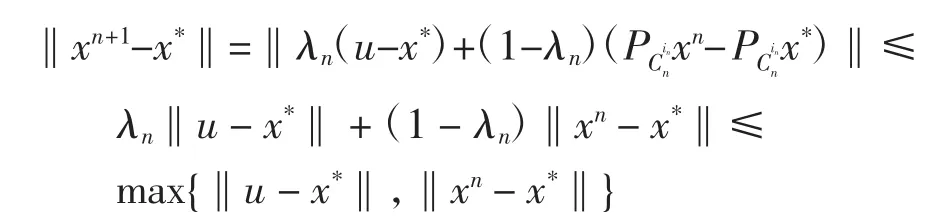
由归纳法知

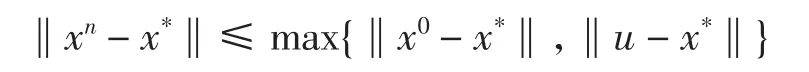
故序列{xn}有界。

2）注意到投影算子是firmly非扩张的，得到

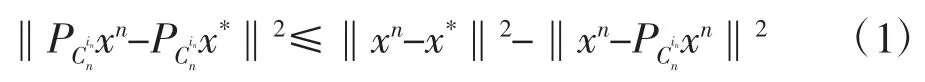
又由引理2，得到

另外，由式（1）和式（2）的第一个不等式得到

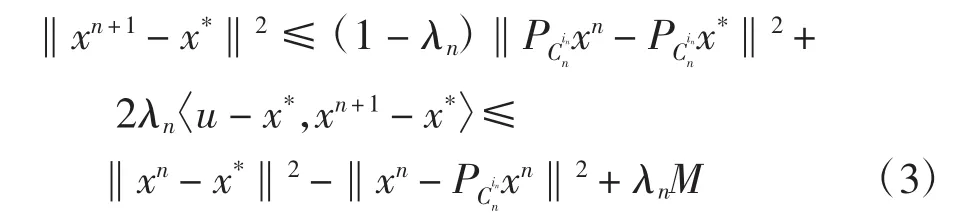
令

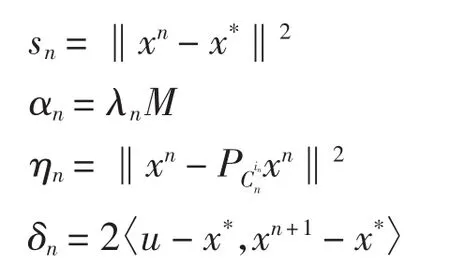
则式（2）和式（3）可被分别改写为如下形式

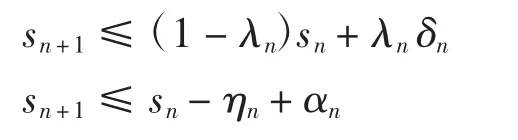
3）注意条件λn→0蕴含αn→0和条件分别成立。为了使用引理3完成定理的证明，需验证对于任一子列{nj}⊂{n}

蕴含着

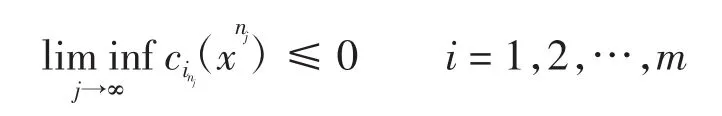
另一方面

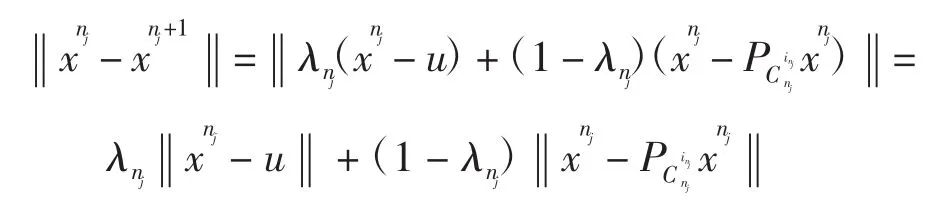
根据引理1，可知

即对于任一子列{nj}⊂{n}，有