基于不同模型的机场客流量预测
刘 夏 ,陈 磊 ,邱 钊 ,陈焕东 ,陈明锐
(1.三亚航空旅游职业学院教务处,海南 三亚 572000;2.海南大学信息科学技术学院,海口 570228;3.海南师范大学教务处,海口 571158)
准确预测机场的客流量,对于机场的运力安排、航线调整及规划发展有着至关重要的作用。在客流量预测方面,众多学者做了相关研究。文献[1]分别采用Holt-winters模型、ARMA模型、一元回归模型,基于近10年的客流量数据预测了未来2年的情况,预测模型仍可改进。文献[2]将时间序列ARIMA模型和BP神经网络模型得到误差平方和,利用权数公式计算得到时间序列ARIMA模型和BP神经网络模型的权值,再根据组合预测模型的计算公式得到预测结果,组合预测结果优于单项预测结果。文献[3]运用灰色预测模型预测了2017年某航线每月的客流量,但预测结果时序图呈线性趋势,预测方法仍可改进。文献[4]运用多元回归分析法建立了旅客吞吐量模型,逐步回归剔除不相关因素后对旅客年吞吐量进行预测,结果显示平均相对误差仅为2.49%,精度较高,但只是基于统计年鉴数据,没有预测每月的旅客吞吐量。文献[5]基于ARIMA模型对时间序列进行回归分析,建立一元线性回归方程,但其一元线性回归方程的变量仅为年份,比多元线性回归方程的预测精度差。文献[6]分别用SPSS、Matlab建立GM(1,1)模型和多元线性回归模型,对未来的入境客流进行预测,预测结果表明,GM模型精度高于多元线性回归模型,但单一模型预测仍欠缺说服力,预测精度仍可改进。文献[7]运用SPSS对安徽省入境游客人数进行二次差分,剔除趋势影响因素,确立预测模型并对未来的人数进行预测,但结果显示短期内的精度较好,长期预测误差大,模型有待改进。文献[8]通过多元线性回归模型和时间序列模型对首都机场2012—2016年的客流量进行预测,并在此基础上采用加权方式进行组合预测,但权重各占50%,说服力不够。文献[9]运用ARIMA模型预测客流吞吐量的线性部分,再用BP神经网络对ARIMA模型的残差进行修正,得到非线性特征趋势后,将ARIMA模型的结果和BP模型的结果进行组合,预测误差值仅为2.12%,但该模型仅是对已有数据的验证,并没有预测未来数据。文献[10]建立 GM(1,1)模型,利用2007—2012年旅游人数的数据,对2013和2014年旅游人数进行预测,并运用移动平均趋势剔除法去除季节影响,对季度城镇旅游人数进行预测,预测值与实际值吻合较好,并依此对2013和2014年季度城镇旅游人数进行预估。
1 数据描述性分析
数据来源于三亚市旅游发展委员会官网的统计数据及三亚凤凰机场提供的真实数据,选取三亚机场2008—2016年每月的客流量进行描述性分析,做出该机场客流量的时序图,如图1所示。

图1 2008—2016年三亚机场每月客流量时序图Fig.1 Sequence chart of monthly passenger flow Sanya Airport 2008—2016
从图1可知,每月客流量具有明显的季节特性,在每年的7~9月旅客人数相对较少,而在1~3月旅客人数明显较多,这和当地的天气等旅游条件有关。统计2008—2016年三亚机场每年的客流量,结果如图2所示。
从图2可知,从2008—2016年三亚机场每年的客流量均保持增长的趋势。从2008年的6 008 308人次增长到2016年的17 850 199人次,年均增长14.88%。统计出2008—2016年三亚机场平均每月的客流量,得到的结果如图3所示。
从图3可知:每年的1~3月、11、12月这5个月的客流量较多,均超过了百万人次;在5、6、9月的客流量较少。呈现明显的季节效应,这与图1的描述一致。
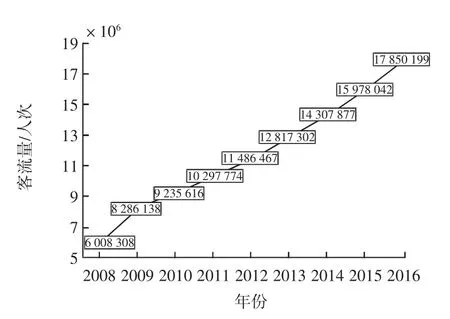
图2 2008—2016年三亚机场每年客流量Fig.2 Annual passenger flow at Sanya Airport 2008—2016

图3 2008—2016年三亚机场平均每月客流量Fig.3 Monthly passenger flow at Sanya Airport 2008—2016 on average
2 预测方法讨论
2.1 ARIMA模型
ARIMA模型又称自回归移动平均模型,是时间序列分析中简单而又实用的模型之一,且预测精度较高。ARIMA模型仅考虑单个变量,试图找出单个变量自身历史走势的规律,进而运用此规律外推以实现预测。
2.1.1 ARIMA模型的形式
设单整序列yt能够通过d次差分将非平稳序列转化为平稳序列,即yt~I(d),则

其中:L 为滞后算子;ωt为平稳序列,即 ωt~I(0),则可对 ωt建立 ARMA(p,q)模型,即

2.1.2 ARIMA模型的识别
ARIMA模型的识别主要是对参数p、d和q的识别。其中,参数d的识别是非平稳序列通过d阶差分变为平稳序列,而p和q的识别主要根据平稳序列的偏自相关函数(PACF)图和自相关函数(ACF)图,具体的识别方法如表1所示。

表1 ARIMA模型识别图形判断方法Tab.1 Identification chart judgement of ARIMA model
根据表1再结合PACF和ACF可有效地识别模型的参数,并对参数进行估计,最后得到预测模型。
2.2 灰色预测模型
邓聚龙[11]提出的灰色系统理论,以“部分信息已知,部分信息未知”的“小样本、贫信息”不确定性系统为研究对象,通过对“部分”已知信息的生成、开发,提取有价值的信息,实现对系统运行行为、演化规律的正确描述和有效监控。鉴于航班上的客流量符合灰色系统的特点,使用灰色预测模型来预测某航线的客流量则有较强的针对性。
2.2.1 模型的建立
首先,假设时间序列 X(0)有 n 个观察值,X(0)={X(0)(1),X(0)(2),…,X(0)(n)},通过累加生成新序列X(1)={X(1)(1),X(1)(2),…,X(1)(n)},则 GM(1,1)模型相应的微分方程为

方程(3)称为白化方程,也称影子方程。其中:a为发展灰数;b为内生控制灰数。
其次,设μ为参数向量,可利用最小二乘法解得
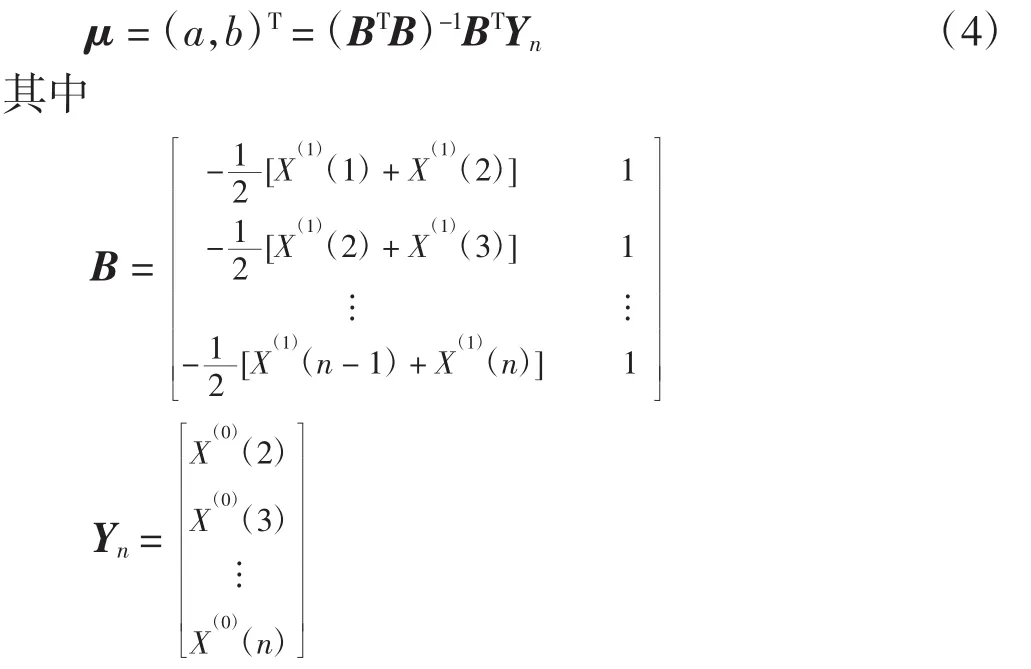
求解微分方程,可得预测模型
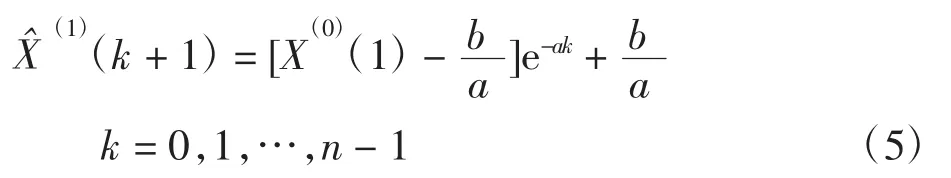
2.2.2 模型检验
灰色预测模型检验主要有:
1)残差检验 计算原始序列及其灰色预测序列之间的绝对误差和相对误差相对误差越小,模型精度越高。
3)后验差检验 首先计算原始序列X(0)的标准差为

然后计算绝对误差序列的标准差为
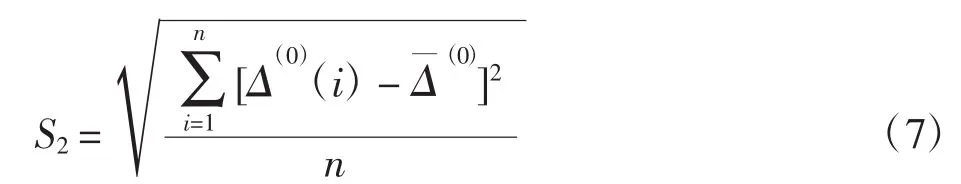
再计算方差比c=S2/S1,最后计算小误差概率p=根据下面预测精度等级划分表确定模型的精度,如表2所示。

表2 预测精度等级划分表Tab.2 Prediction accuracy level
若残差检验、关联度检验及后验差检验都通过,则可用所建模型进行预测,采用分组预测的方法对航线每月客流量进行预测,最后计算预测精度。
2.3 回归与ARMA模型
2.3.1 模型定义及形式
如果能把回归模型的误差项进一步建立成时间序列模型,称此模型为回归与ARMA组合模型,该模型有时会得到比单一方法更好的预测结果。若有如下多元线性回归模型为
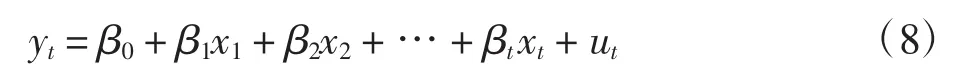
其中:xt为解释变量;yt为被解释变量;ut为随机误差项,通常满足假定条件。当ut存在自相关时,时间序列分析的一个有效应用是对残差序列ut建立ARMA模型,即ut=Φ-1(L)Θvt,代入式(8)可得回归与时间序列相结合的模型为
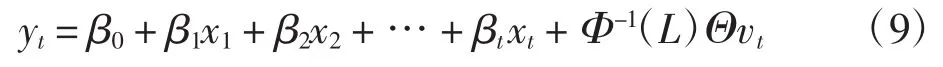
其中:vt是满足全部假定条件的误差项,vt的方差一般与ut不同。
2.3.2 模型意义
如果从回归模型的角度理解,则是用时间序列模型进一步描述不符合假定条件的误差项。如果从时间序列模型的角度理解,则是把回归部分看成从被解释变量中剔除解释变量的确定性影响后,对一个不含任何确定性成分的平稳随机序列建立时间序列模型。
3 模型实证预测
3.1 基于ARMA模型预测
用传统的时间序列ARMA模型,对上述的每月客流量进行拟合和预测。在建立ARMA模型前,根据图1可得三亚机场的客流量呈现明显的季节特性。采用X12的季节调整法对每月的客流量进行季节调整,得到的是每月季节指数,如表3所示。
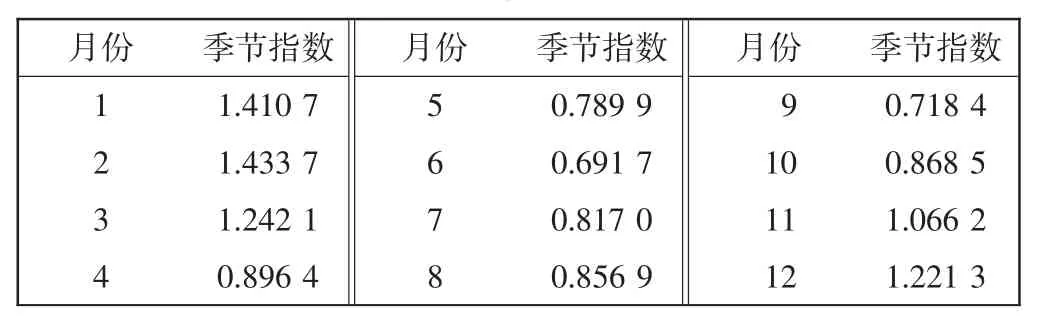
表3 每月季节指数Tab.3 Monthly seasonal indices
对调整后的月客流量进行单位根检验,检验结果如表4所示。

表4 调整后客流量的单位根检验结果Tab.4 Unit root test result of passenger flow after adjustment
根据表4可得,调整后客流量序列可使原序列平稳,所以应建立 ARMA(p,0,q)模型,即 ARMA(p,q)。
3.1.1 模型建立
通过NUM的PACF和ACF图,对p、q进行识别,所得结果如图4所示。

图4 NUM的PACF和ACF图Fig.4 PACF and ACF charts of NUM
根据图4的ACF和PACF可知,序列Y对应的PACF图表现出2期“截尾”的现象,而ACF图则表现为“拖尾”现象,所以对机场每月客流量初步建立ARMA(2,1)。经过反复调试,最终建立 ARMA(2,1)模型的结果如表5所示。
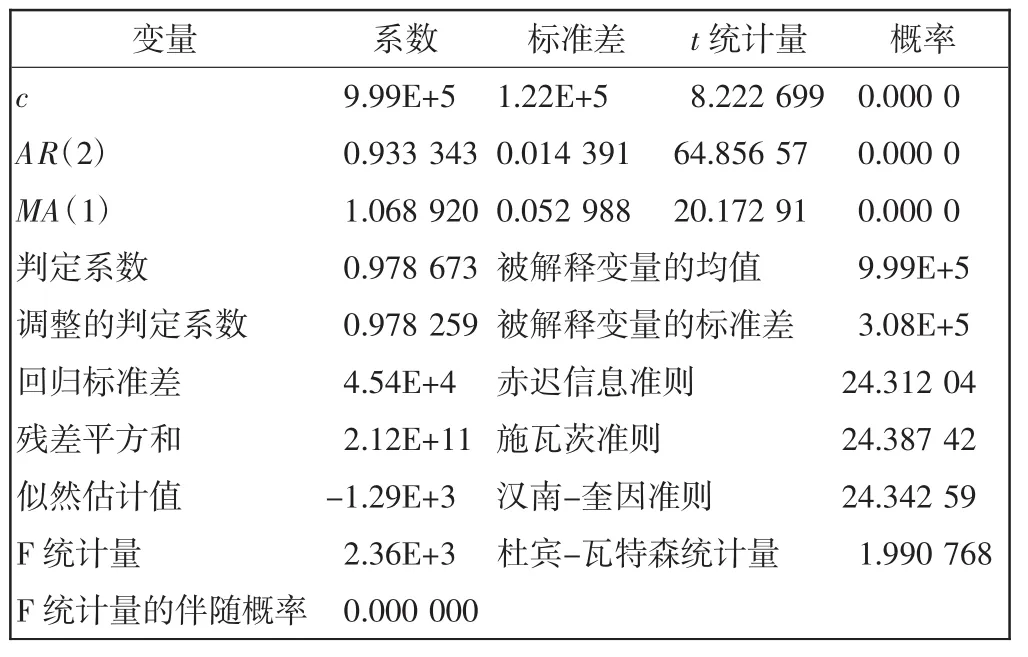
表5 ARMA的结果Tab.5 ARMA result
根据表5可得,在0.05的显著水平下,模型总体的似然比检验显著。ARMA(2,1)的各项系数均是显著的,得到具体的方程为
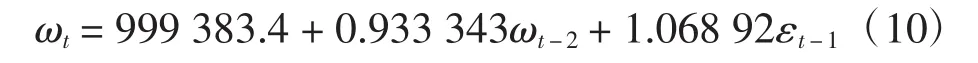
3.1.2 模型检验
对上述模型的残差进行检验,画出残差的PACF和ACF图,观察其模型是否提取了客流量序列全部的有效信息,所得结果如图5所示。

图5 残差的PACF和ACF图Fig.5 Residual PACF and ACF
根据图5可看出残差序列的PACF和ACF均在两个标准差之后,说明上述模型有效地提取了序列的全部信息。利用建立的ARMA(2,1)模型对机场内的每月客流量进行预测。
3.1.3 模型预测
经过上述的模型建立和检验,利用该ARMA(2,1)模型对样本内机场的每月客流量进行预测,得到预测序列Yj′再乘以相应月份的季节指数Sj(参见表3),得到最后的预测序列。以1月份为例,预测序列可表示如下

其中,YF1为1月份客流量的预测序列。1月份预测的平均绝对百分误差为
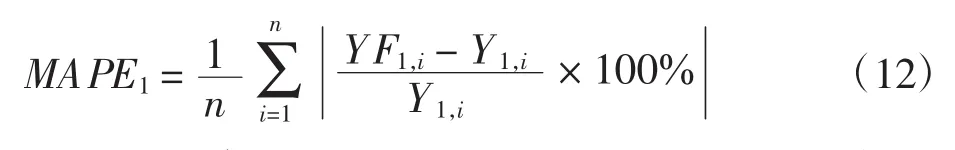
根据上述建立的ARMA(2,1)对三亚机场的每月客流量进行预测的MAPE=4.20%。
3.2 灰色预测模型
根据图1可看出,2008—2016年三亚机场的客流量具有明显的季节特性,下面采用2008—2016年每月对应的客流量作为原始序列建立灰色预测模型,采用分组预测可有效地避免季节效应对预测的影响。
3.2.1 模型建立
以2008—2016年1月份的客流量为例建立具体的灰色预测模型。首先,令


3.2.2 模型检验
同样的方法可得到三亚机场1~12月份的预测模型,下面利用R3.2.3软件得到各模型的检验参数,所得结果如表6所示。

表6 模型检验参数Tab.6 Test parameters of model
根据表6可知,各月的预测精度等级为好,且MAPE=4.19%,总体预测精度较好。
3.3 基于ARMA改进回归模型
选用起降架次S、行李量LUG和客座率PLF这3个指标作为解释变量,以回归作为被解释变量,建立回归模型。以2008—2015年的数据作为训练样本集,以2016年的数据作为测试数据集,对上述建立的回归模型的预测能力进行评价。
在训练样本数据集上建立回归模型,所得回归结果如表7所示。

表7 回归结果Tab.7 Regression results
根据表7可得,总体回归方程在0.05的显著水平下是显著的,且起降架次S、行李量LUG和客座率PLF的回归系数的显著性检验的p值均小于0.05的显著水平,说明三者对客流量具有显著性影响,得到的回归方程为

对上述建立的模型进行自相关检验,所得到的结果如表8所示。

表8 回归方程的异方差检验结果Tab.8 Heterosced asticity test result of regression equation
根据表8可得,在0.05显著水平下建立的回归模型拟合的残差存在自相关,对上述建立的回归模型的残差建立ARMA(2,1)模型,所得结果如表9所示。
根据表9可得,在0.05的显著水平下总体方程和各变量的系数均是显著的,可得到ARMA(2,1)模型的表达式为

利用上述的回归模型对训练样本集进行预测,并建立ARMA(2,1)对回归的残差进行拟合,得到预测结果的MAPE=1.67%。利用建立的ARMA改进回归模型对2016年每月的客流量进行预测,所得结果如表10所示。
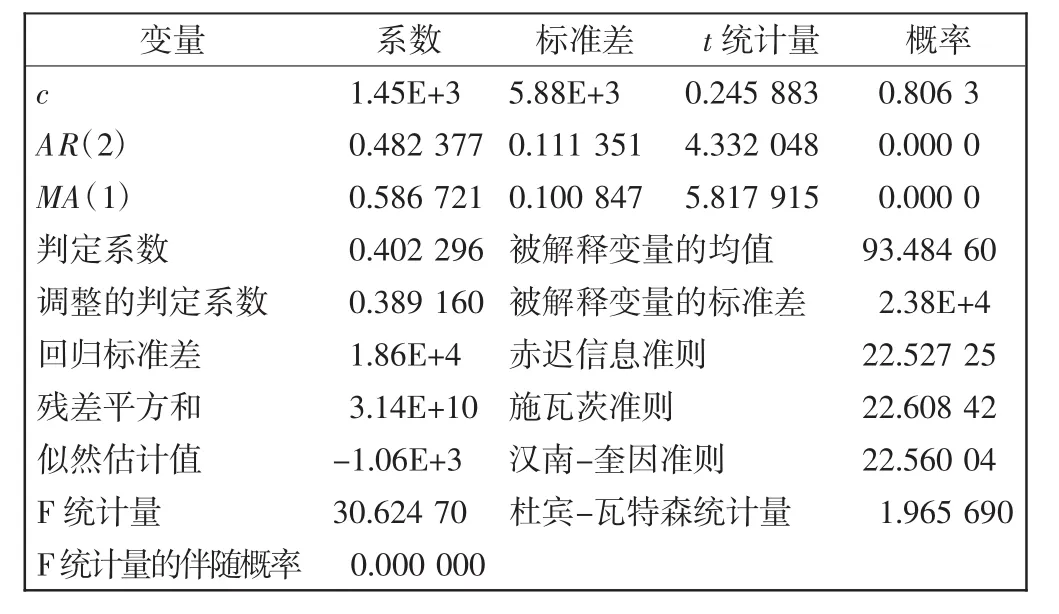
表9 ARMA模型残差回归结果Tab.9 Regression residue result of ARMA model

表10 2016年每月客流量的预测Tab.10 Predicted passenger flow in 2016
根据表10可得,基于ARMA改进的回归模型对2016年机场客流量的预测与真实值比较接近,说明基于ARMA改进后的回归模型具有很好的预测能力。
4 对比分析
将3个模型得到的预测值与真实的客流量进行对比,所得结果如图6所示。
计算3个模型的平均绝对百分误差,所得结果如表11所示。
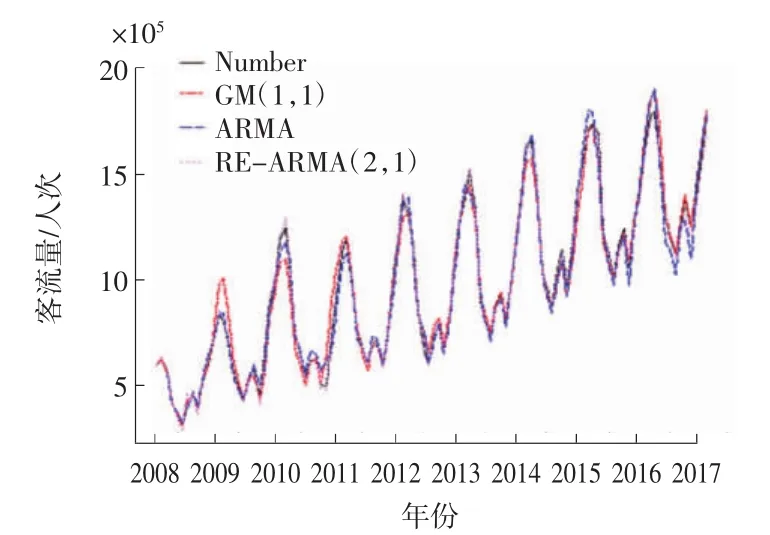
图6 不同模型的预测值比较Fig.6 Predicted value comparision of different models

表11 3个模型的MAPE值Tab.11 MAPE values of three models
根据表11可得,ARMA模型和改进后的GM(1,1)模型的预测精度相差不大,而基于ARMA改进后的回归RE-ARMA(2,1)模型相对于其他2种模型更精确。说明RE-ARMA(2,1)模型对机场的客流量有很好的预测能力。因无法得到2017年的起降架次S、行李量LUG和客座率PLF的数据,所以暂时无法对未来进行预测。一方面,由于采用分组预测,灰色模型对小样本和数据信息量少的情况,具有很强的针对性。另一方面,采用ARMA模型对未来2年的机场客流量进行预测,预测时间跨度较大,误差较大,而灰色预测具有较好的针对性。基于上述两方面的原因,采用灰色预测模型对2017和2018年三亚机场的客流量进行预测,所得结果如表12所示。

表12 2017年和2018年每月客流量的预测Tab.12 Passenger flow prediction each month in 2017 and 2018
5 结语
通过上述的建模与分析,对不同的模型进行比较,最后选定适用于小样本预测且精度较高的灰色预测模型。灰色预测模型可以较为准确地预测未来2年三亚机场的客流量,对该机场的发展具有重要的指导意义和实践价值。
未来2年的客流量预测结果不仅可供市政府相关部门参考,制定旅游业、交通运输业发展规划,也可提供给机场作为调配运力、增开航线、调整时刻容量及改、扩建的参考依据。

