基于改进灰色Markov链的民机偶然损伤预测模型
贾宝惠,耿喆元,蔺越国,王毅强
(中国民航大学航空工程学院,天津 300300)
偶然损伤是飞机结构损伤的三大来源之一[1],是飞机在使用期间受到随机事件或非计划事件影响而造成飞机结构出现损伤,其表现为变形、开裂、穿孔或其它受损结构、分层或脱胶。民用飞机维修大纲的制定有利于对飞机的偶然损伤进行恰当的维修和维护,其具有重要意义[2]。偶然损伤贯穿民用飞机使用的全过程,具有随机性和偶然性,因而维修大纲中偶然损伤的维修等级和维修间隔较难界定。
民航事故征候,是指在航空器运行阶段或在机场活动区内发生的与航空器有关的、不构成事故但影响或可能影响安全的事件[3]。ICAO安全管理手册中描述了事故、事故征候及近似事故征候之间的关系,即每一起事故发生前,平均有29起事故征候和300起近似事故征候发生[4]。因此对偶然损伤事故征候的分析和预测与航空安全息息相关。
灰色系统理论是由邓聚龙[5]提出的一种新方法,主要研究“小样本、贫信息”的不确定性系统,目前已广泛应用于电力、生物医学、机械等领域[6-9]。GM(1,1)模型是灰色系统中最常用的一个模型,其本质是以指数型曲线去拟合原始数据,继而预测出一条较为平滑的曲线。但GM(1,1)模型对于波动性较大的数据列拟合较差、预测精度较低,而Markov预测理论以其独有的无后效性,即系统将来所处状态只与系统现在的状态有关,而与系统过去的状态无关,可对灰色模型进行修正。灰色马尔可夫模型,一方面利用GM(1,1)模型使数据序列满足了马尔可夫的前提条件,即无后效性和平稳过程等均值特点;另一方面,马尔可夫模型又解决了对随机波动性较大序列的预测问题,提高了预测精度,在交通、商业、林业、能源等领域得到应用[10-12]。
偶然损伤事故征候受到天气因素、机械、地面保障、机组、机务、空管或其他不可控因素影响,属于动态的时变系统。利用灰色马尔可夫模型建立偶然损伤事故征候的预测模型,并利用新陈代谢法进行改进,避免了专家打分带来的主观影响,可以对短期和中长期的偶然损伤事故征候进行预测,为偶然损伤的预防性维修方案提供预测模型支持。
1 灰色马尔可夫模型的建立
1.1 灰色 GM(1,1)模型
灰色系统预测模型具有所需信息较少、计算简便、精度较高等特点。灰色GM(1,1)模型建模过程如下:
1)给定原始的数据序列
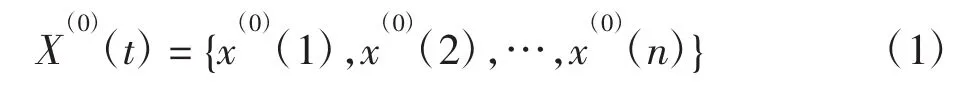

3)构造数据矩阵B和数据向量Y,即
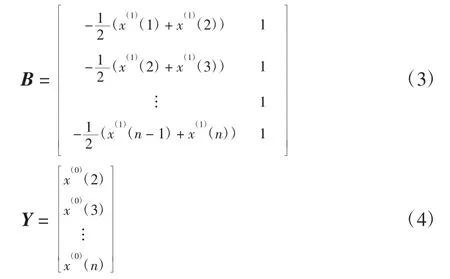
4)由累加生成的数列X(1)得到白化微分方程

5)根据最小二乘估计算法得到白化微分方程中的参数a、u为

6)将求解出的参数向量代入微分方程,对微分方程进行求解,得到 GM(1,1)模型

7)将上式进行累减还原,得到预测值
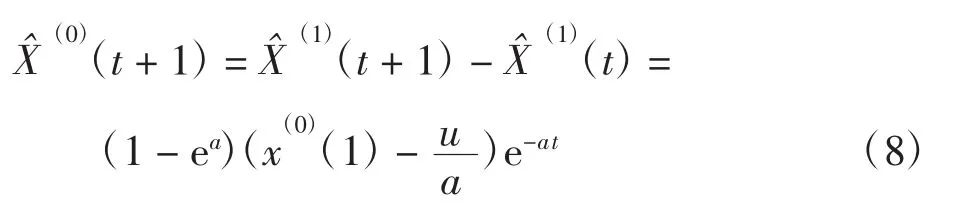
其中:a为发展系数;b为灰色作用量。
8)对预测值进行精度检验:
残差公式为

相对误差公式为

9)后验差检验:
a)原始数列的均值为

b)原始数列的方差为

c)残差的均值为

d)残差的方差为

e)后验差比值为

f)小误差概率为

表1给出了各指标值的大小与模型精度之间的关系,如果一个灰色模型的相对误差△t、后验差比值C、小误差概率P都处于“好”的等级,则认为该模型精度较高,适合应用。灰色模型建立的流程图如图1所示。

表1 模型精度检验等级Tab.1 Model accuracy testing level

图1 灰色GM(1,1)模型预测体系Fig.1 Forecast system based on GM(1,1)model
1.2 状态划分
马尔可夫模型中状态划分常用样本均方差法、模糊聚类法和有序聚类法这三种方法来定义状态区间,实际问题中统计指标值均按一定次序排列,在划定状态时不能随意调整。偶然损伤事件事故征候的统计数据与年份紧密相关,打乱顺序会破坏事实原有的客观性。因此采用有序聚类的方法将偶然损伤事故征候分成n个状态。其任意一个状态可表示为

马尔可夫链的最终预测值也一定落在某个[⊕1i,⊕2i]区间内,因此可用区间的中值去估计预测值,即

1.3 灰色马尔可夫模型
已知过程在t0时刻所处的状态,系统在t>t0所处状态的分布及过程与t0之前所处的状态无关,只与现在的状态有关,则称之为马尔可夫过程。而时间和状态都离散的马尔可夫过程称作马尔可夫链。依据C-K方程

可以根据已知现在的分布和构造转移矩阵的方法来预测未来状态。一般地,用fij表示从状态i转移到状态j的频数。根据概率的稳定性,可以近似地用转移频率来估计转移概率,即,其中Pij为转移概率,表示从状态i到状态j的概率。由Pij组成的矩阵就是马尔可夫链中的状态转移矩阵,即


图2 灰色马尔可夫链模型建模流程图Fig.2 GM(1,1)chain modeling flowchart
2 偶然损伤事故征候预测实例
采用《中国民用航空安全信息分析报告》,针对2005—2014年偶然损伤事故征候的统计数据,如表2所示,检验灰色马尔可夫模型的精度并对偶然损伤事故征候进行预测。

表2 2005—2014中国偶然损伤事故征候事件数Tab.2 Accidental damage incidents in China 2005—2014
2.1 建立 GM(1,1)模型
根据1.1节中的GM(1,1)模型,用Matlab编写程序求得系数矩阵为
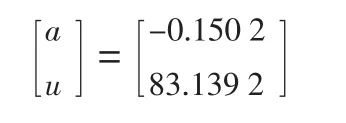
将 a=-0.150 2,u=83.139 2代入式(7)得


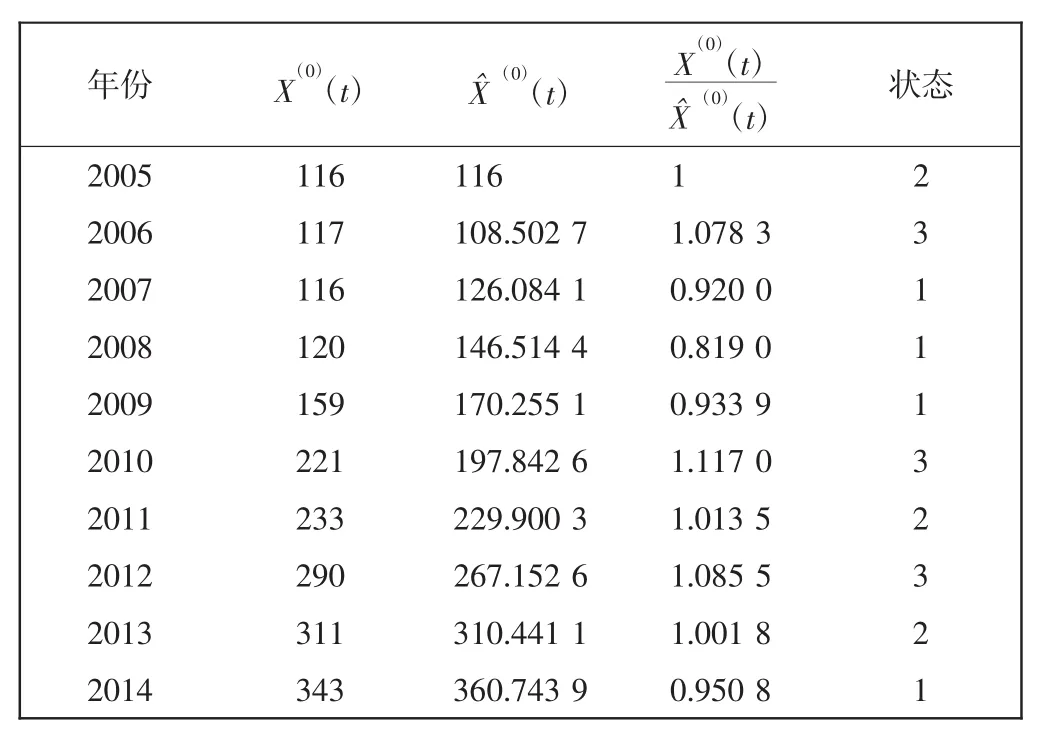
表3 灰色模型预测值与实际值对照及状态划分Tab.3 Comparison and state devision between GM(1,1)forecast and actual values
对灰色模型进行精度校核,分别计算残差检验Δt、后验差检验C和小误差概率P,结果如表4所示。

表4 精度检验Tab.4 Accuracy test
根据表1中的精度标准,表4中的后验差比值C=0.182 6,小于 0.35,小误差概率 P=1,大于 0.95,所以GM(1,1)模型在偶然损伤事故征候中的应用程度为“好”。
2.2 状态划分
依据1.2节中灰色模型的状态划分方法,根据实际值与预测值的比值,得到灰色GM(1,1)模型预测的相对变化率,依据相对变化率将偶然损伤事故征候转化为⊕1、⊕2、⊕3这3个状态,如表5所示。

表5 偶然损伤事故征候状态划分Tab.5 State division of accidental damage incidents
根据表5的状态划分区间,2002—2012中的数据状态划分结果如表3所示。
2.3 计算预测值
由表3得到马尔可夫模型的一步转移矩阵为

因为2014年的状态处于⊕1,所以初始概率矩阵为Pa(0)=(1 0 0),则根据C-K状态方程,2015年的状态分布概率为
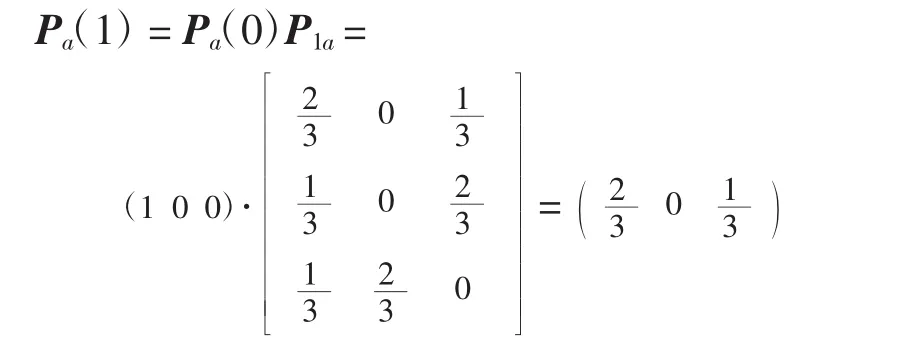
因此,2015年的状态有66.67%的可能性处于状态 1,根据⊕1的比值范围是⊕1=[0.819 0,0.999 6],结合灰色GM(1,1)模型对2015年的预测数值为419.197 6,可以求得2015年偶然损伤事故征候的事件数(0)(11)∈(343.322 8,419.029 9),而 2015 年偶然损伤事故征候的实际值为394,取值显然在上述区间内。可用区间的中值381.18去估计2015年偶然损伤事故征候的预测值,但利用马尔可夫转移矩阵对灰色模型预测的结果进行修正,可以得到精度更高的预测值。
图3显示了灰色模型与灰色马尔可夫模型对偶然损伤事故征候的预测结果。由图3可知,灰色模型在2005—2014年期间对偶然损伤总数事故征候趋势的预测与实际值基本吻合,2011年、2013年的预测结果和真实值几乎重合。但从2015年的预测结果看,灰色马尔可夫模型的预测结果更接近真实值,也就是预测更加精准。

图3 偶然损伤事故征候的预测及实际值Fig.3 Accidental damage incident forecast and actual values
下面预测2016年的偶然损伤事故征候所处的状态。根据C-K状态方程,由于2016年位于最后一个年份及2014年之后的第2个时刻,所以考虑用两步转移矩阵,即

则2016年的状态分布概率为

所以,根据马尔可夫链的预测结果,2016年的偶然损伤事故征候状态应该处于状态⊕1,但实际上2016年的偶然损伤事故征候数为548,与灰色模型在2016年预测值的比值是1.125 0,已超出了之前划分的状态,更不可能在状态⊕1。造成这种结果的原因不是由于模型出现了错误,而是在2005年航空安全信息网的使用还没有普及,仅依靠各大航空公司自觉上传数据,很多数据不完全。而2016年全新的航空信息安全平台上线后,样本数据量增加了,2005年的数据显得过于陈旧,因此,在预测新一年的事故征候时,使用新陈代谢的灰色马尔可夫模型进行修正和预测。
2.4 改进的灰色马尔可夫模型的预测
新陈代谢GM(1,1)模型的建模思路是,去除原始数据中最旧数据(即2005年的数值),补充通过GM(1,1)模型刚刚预测出的2015年的事故征候值419,计算出新的GM(1,1)模型的系数矩阵为

新的预测模型为

根据新的 GM(1,1)模型,计算出 2006—2016年的偶然损伤事故征候的预测值如表6所示。
改进模型的精度检验如表7所示,后验差比值C=0.149 9,小于 0.35,小误差概率 P=1,大于 0.95,所以GM(1,1)模型在偶然损伤事故征候中的应用程度为“好”。依据相对变化率将偶然损伤事故征候转化为⊕1、⊕2、⊕33个状态,如表 8 所示。
依据表8的状态划分区间,将2005—2014年的数据状态划分结果列于表6。由表6得到计算所得新转移概率矩阵为
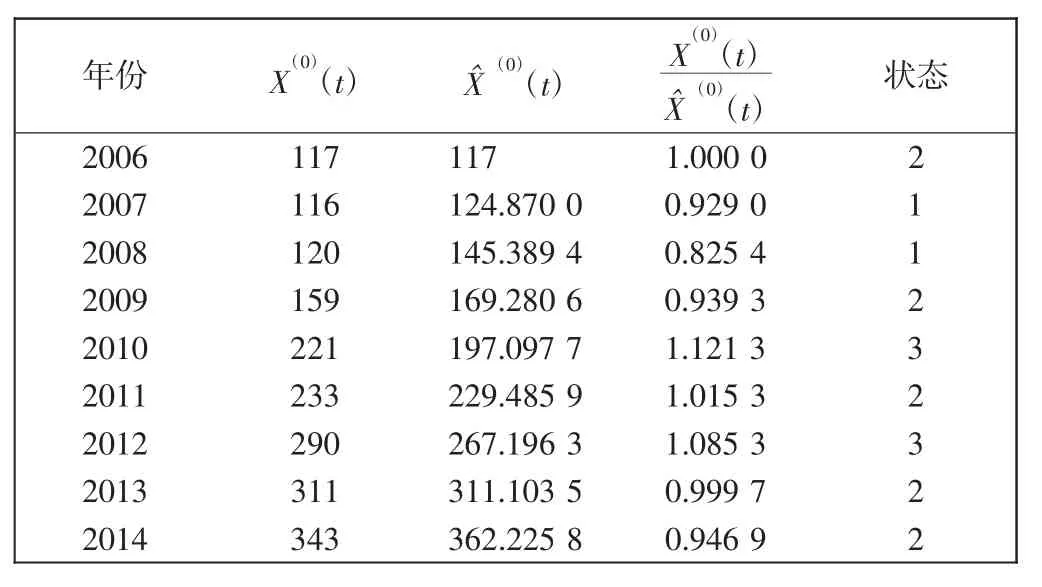
表6 新陈代谢灰色模型预测值与实际值对照及状态划分Tab.6 Comparison and state devision between metabolism GM(1,1)forecast values and original data

表7 改进模型精度检验Tab.7 Accuracy test of advanced model

表8 改进模型偶然损伤事故状态划分Tab.8 State division of accidental damage incidents for advanced model

由于2015年新的GM(1,1)模型的预测值为421,而真实值为394,其相对变化率为0.934 2,因此2015年的偶然损伤事故征候在新陈代谢灰色马尔可夫模型处于状态⊕2,所以初始概率矩阵为Pa(0)=(0 1 0),则根据C-K状态方程,2016年的状态分布概率为

因此,2016年的状态有50%的可能处于状态3,根据⊕3的比值范围是⊕3=[1.082 4,1.121 3],结合灰色GM(1,1)模型对2015年的预测数值为491.052 8,可得2016年的预测区间为(531.458 4,550.617 5),而2016年偶然损伤事故征候的实际值为548,显然在此区间内,用中值去估计预测值为541.07,显然利用新陈代谢灰色GM(1,1)模型可以抵消陈旧数据对模型的影响,也可以对未来年份的预测得到更精确的结果,其精度亦得到了提高。GM(1,1)模型、灰色马尔可夫模型和改进的灰色马尔可夫模型的预测结果和精度比较如表9所示,新的模型曲线如图4所示。

表9 三种模型的预测结果和精度比较Tab.9 Comparison of forecast results and accuracy by three models

图4 3种模型对偶然损伤事故征侯的预测与实际值Fig.4 Accidental damage incident forecast and actual values by three models
其中预测精度的计算公式为

由图4可知,GM(1,1)模型的预测曲线与偶然损伤原始数据的趋势大致相同,可以较好地拟合偶然损伤的发展状态。灰色马尔可夫模型通过转移矩阵对灰色模型进行修正,得到了更为接近真实值的结果。改进的灰色马尔可夫模型通过新陈代谢的方法,去掉旧的数据,加入灰色模型预测出的新数据,曲线趋势并没有明显变化,但是恰恰可以弥补灰色马尔可夫模型对中长期预测的不足,使2016年的预测精度达到98%以上。
3 结语
偶然事故征候属于少样本、贫数据的随机系统。GM(1,1)模型对以年份作为基本时刻的偶然损伤事故征候预测效果较好,某些年份的预测值和真实值近似重合,表明利用GM(1,1)模型预测偶然损伤事故征候是有效的。灰色马尔可夫模型是在GM(1,1)模型预测的基础上,凭借马尔可夫模型对无后效性事件预测上的优势,利用转移矩阵对GM(1,1)的预测结果进行修正。修正之后精度明显提升,可以有效地估计未来一年的偶然损伤事故征候数量。新陈代谢的灰色马尔可夫模型,抵消了陈旧数据对模型预测的影响,改进之后可以预测未来中长期的发展趋势,为偶然损伤可能性等级的评定以及预防性维修大纲的制定提供参考。

