基于植物生物学参数的多枝柽柳耗水量估算方法
李 双,杜建括
(陕西理工大学历史文化与旅游学院,陕西 汉中 723001)
我国荒漠区植被以耐旱草本和灌木为主。了解干旱荒漠区灌木个体和群丛对有限水资源的消耗量,对于研究荒漠植被的生长状况、个体和群落尺度的水量平衡至关重要。目前,基于植物个体和林分水平研究植物耗水过程的方法很多。测定林分水平耗水的方法大致可以分为两类,一类是直接测定的方法,主要包括空气动力学法、涡动相关法、Penman-Monteith方程法、水分平衡法、能量平衡-波文比法和红外遥感法[1];另一类方法是借助一定的尺度转换参数,由单株/木耗水推求林分水平的耗水信息[2]。基于尺度转换的林分蒸腾耗水量通常可以依据液流与胸径[3,4]、茎干横截面积[5,6]、边材面积[7]、叶面积[1,2]的关系以及植被种植密度[8]和单株木占地面积[9]等进行尺度扩展后求得。选择何种尺度扩展方法推求林分蒸腾主要取决于植被群落特征[10]。在个体尺度水平上,测定植物耗水的方法主要有整树容器法、风调室法、盆栽法、蒸渗仪法、液流测定法(同位素示踪法和热力学方法)。热力学技术实现了对植物茎干液流实时、准确、高时间分辨率的自动监测[11,12],已在草本、农作物、乔木和灌木耗水研究方面得到广泛应用[13]。
灌木没有明显主干或主干很短,热平衡液流仪通常监测的是灌木单枝耗水量,需要借助合适的尺度转换参数来推导和获取单株、灌丛群落的耗水量。已有学者通过茎流与茎干横截面积[6]、叶面积[1,2,14]的函数关系推算了灌木单株和群落的蒸腾耗水量,取得了较好的实验结果。在干旱荒漠区,灌木等植被的分布相对稀疏,阳光照射时冠层叶片之间相互遮挡的程度不高,灌丛群落耗水量与叶片总面积之间存在着极强的相关性[2]。但与灌丛叶片总面积相比,叶片总干重更容易直接获取,若荒漠植被蒸腾耗水与叶片干重显著相关,则叶干重可作为扩展参数推求单株、灌丛尺度的耗水量。
近些年来,在我国西北荒漠植物耗水与生态需水量计算方面已取得一些成果[15-19],但基于茎干液流量与植物形态参数估算小尺度范围柽柳耗水的研究很少。本文选择甘肃省景泰县寺滩乡典型荒漠灌木多枝柽柳作为研究对象,在单枝茎流测定基础上,以叶干重作为扩展变量来推算单株蒸腾耗水量,并对样地柽柳总耗水量作估算,旨在寻求一种适合小尺度范围或种植布局和长势较统一的灌丛单株/群落蒸腾耗水量的测量方法和理论,为科学评价荒漠区水分平衡及人工植被管理提供一定依据。
1 研究区概况
甘肃省景泰县寺滩乡位于黄土高原与腾格里沙漠过渡地带,属于温带大陆性干旱气候,海拔1 828 m(37°14′N,103°48′E),年均气温8.6 ℃,极端最高气温为38.6 ℃,极端最低气温-27.3 ℃,≥0 ℃的年活动积温3 614.8 ℃,≥10 ℃的年有效积温3 038 ℃,无霜期120 d左右,年日照时数2 723.9 h。年平均降雨量180 mm,降水分配不均,夏秋多雨,冬春干旱,约60%的降水集中在7-9月,年潜在蒸发量3 038 mm。风沙日数较多,平均风速2.0~3.1 m/s,瞬时最大风速可达21.7 m/s。土壤类型以灰钙土和灰棕荒漠土为主。
为了保护脆弱的生态环境,研究区为2003年退耕后种植的多枝柽柳(以下简称柽柳)生态建设林用地。柽柳行株距为4×2 m。林地内草本植物主要有碱蓬(Suaedaglauca)和灰藜(Chenopodium album Linn.)等。柽柳的平均株高170 cm,茎干基径平均为3.2 cm。本区地下水埋藏较深,无人工灌溉柽柳生长的水源主要来自于大气降水和土壤水。
2 研究方法
2.1 茎干液流测定
在研究区选择一块50 m×50 m的样地进行植被调查和茎流监测。选择长势良好、健康的柽柳作为样本,使用热平衡茎流仪(Flow 32, Dynamax Inc., Houston, TX, USA)监测它们的液流速率变化。使用游标卡尺测量茎干直径范围以选取合适的茎流仪探头型号。2013年6-9月、2014年6月和8月均在研究区样地开展了柽柳茎干液流监测。数据采集器(CR1000, Campbell Scientific, Logan, UT, USA)每10 s扫描一次,每1 min平均一次,每6 min记录一次数据。实验期间用到的探头型号有SGA10、SGA13、SGB16、SGB19和SGB25,每个探头有2~3个重复。
2.2 地上生物参数的测定
2014年6月和8月分别选取柽柳个体各6株,共计12株作为标准木,在其上安装热平衡液流仪传感器。每一块样地内地形平坦,同一立地条件下绝大多数柽柳个体差异不显著。测量所选样株的冠幅大小(东西、南北长)、株高、所有枝条的基径和长度。每株柽柳样本中选取3个枝条,其中至少有1个来自包裹着传感器的枝条,共计36枝,采集其上的所有叶片,每枝的叶片单独装入样品袋,带回实验室,于80 ℃鼓风恒温烘箱中烘至恒重,获得叶片干物质量。其中24枝样品的叶干重及枝条基径、长度用于建立单枝叶干重与枝条基径、长度的关系模型,其余12枝用于模型检验。
(1)柽柳单枝叶干重估算模型。参考董道瑞等[20]关于塔里木河下游柽柳地上生物量估算方法,根据单枝柽柳的基径和长度,用线性、幂、对数和指数4种函数形式来建立柽柳单枝叶干物质量的估算模型,并用决定系数R2和F检验对拟合的回归方程进行评判,从中选出最优估算模型。
w=a(d2h)+b
(1)
w=a(d2h)b
(2)
w=aln (d2h)+b
(3)
w=aebd2h
(4)
式中:w为单枝叶干重,g;d为单枝柽柳的基径,cm;h为单枝柽柳的长度,cm;a、b均为系数。
(2)柽柳单株叶干重估算模型。根据12株样本所有枝条的基径和长度数据,利用从公式(1)~(4)中选出的最优单枝叶干重估算模型获得每株柽柳叶干总干重,其表达式为:
Wi=niwi(i=1,2,…,12)
(5)

利用公式(5)计算的单株叶片总干重,结合每株样本的冠幅及株高,建立单株叶片总干重与冠幅周长和株高之间的函数关系式,其表达式为:
W=a+b(P2H)c
(6)
P=2 πs+4 (l-s)
(7)
式中:W为单株柽柳叶片总干重,g;P为冠幅周长,m;H为株高,m;s为冠幅的短半径,m;l为冠幅的长半径,m;a、b和c均为系数。
2.3 快速称重法测蒸腾
试验地柽柳快速离体称重法参考杨劼等[21]离体称重测定人工灌木蒸腾强度的方法,在包裹液流仪探头的柽柳植物附近选择一株长势和大小较一致的柽柳,在植株冠层中部四周剪取长5~10 cm的枝条6~8个,剪下后立即用精度为0.001 g的电子天平称重,记为W1,并记录称重时间;称重后将枝条迅速放回原处,使离体枝条处在原来的环境下蒸腾,3 min后取下迅速重新称重W2,两次重量之差即为蒸腾耗水量。本实验设计6次重复以减少蒸腾失水误差,每间隔1 h做一组实验。将第二次称重后的枝条摘下叶片(包括嫩梢),并装入已知重量的信封,带回实验室烘干样品,称重,净叶片干重用Wd表示。利用以下公式即可求出柽柳蒸腾速率 。
Tr=60 (W1-W2)/Wd/t
(8)
式中:Tr为蒸腾速率,g/(g·h);W1为离体枝叶的初始重量,g;W2为离体枝叶的t分钟后的重量,g;t为两次称重的蒸腾时间间隔,min;Wd为叶片净干重,g。
3 结果与分析
3.1 柽柳茎干液流与形态参数的关系
为了同一尺度水平上比较不同单位表示的液流速率变化的差异性,单位横截面积和单位叶干重表示的液流速率分别乘以系数2和100,这样3种单位表达的液流速率数值均介于0~300之间(图1)。无论用何种单位表示液流速率,3个茎干的液流变化趋势相同,但3种单位表示的不同径级枝条液流速率间的差异明显不同,例如,用单位时间通过横截面的液流量表示的柽柳不同径级间的液流速率相差显著[图1(a)];用单位时间通过2个单位横截面积的液流量表示的各茎干间液流值差异略微缩小,尤其是枝条S1与S2的液流速率相近[图1(b)];用单位时间每100 g叶干重的液流量表示的不同茎干液流变化的曲线彼此间几乎相互重叠[图1(c)],说明柽柳茎干液流与枝条叶干重密切相关,液流量主要是由枝条叶片量决定的,经叶干重标准化处理后可以很好地消除不同枝茎干液流的差异。
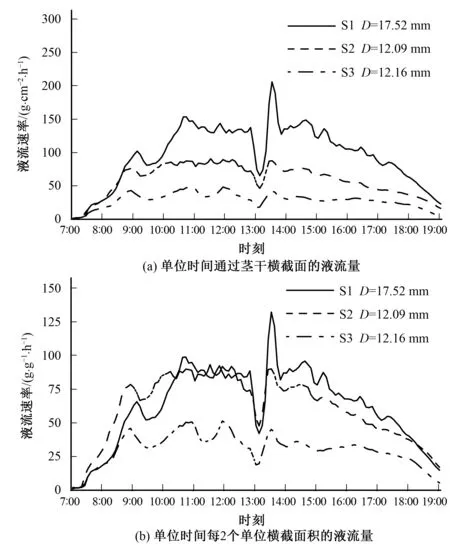

图1 不同单位表示的柽柳不同枝条液流速率变化的日过程
为进一步明确柽柳液流量与生态学参数的相关性,对其进行了线性回归分析。柽柳7∶00至19∶00累计液流量与茎干边材面积、横截面周长和面积的相关度R2分别为0.739、0.669和0.679(P<0.001)[图2(a)~图2(c)],而与叶干重存在极其显著的正相关(R2=0.965,P<0.001)[图2(d)]。虽然柽柳液流量与枝条断面参数整体上呈正相关,但也可能出现例外,譬如,直径12.09 mm茎干的液流速率始终大于直径12.16 mm茎干的液流速率,表明液流与茎干直径没有很好的一致性,类似结果也存在于液流与茎干横截面积之间。图1和图2揭示了与茎干直径和横截面积相比,叶干重作为一个基础参数用于植物耗水研究将更加准确和有效。因此,本文将叶干重作为扩展参数来获取整株或灌丛尺度的耗水量是可行的。
3.2 柽柳单枝/株叶片总干重的估算
3.2.1 柽柳单枝叶片总干重回归模型
选取12株柽柳中的24个单枝样本,在SPSS17.0统计分析软件中利用公式(1)~(4)构建4种函数形式的生物量估测回归模型(见表1)。经查F值表,F0.01(1,22)=7.94,结合表1可知,4种拟合函数均通过显著性检验,且线性函数的R2值最高,故认为估算柽柳单枝叶片总干重的最优模型为:
w=0.074 (d2h)+14.538 (9)

表1 4种函数拟合的柽柳单枝叶片总干重回归方程统计分析表
注:**表示显著性水平P<0.01。
用其余的12个单枝样本对线性模型进行检验,均方根误差RMSE为2.014 g,实测值与模拟值的斜率为0.937,接近1(见图3)。所以,利用基径平方与长度乘积建立的枝条叶片总干重线性模型是可信的。
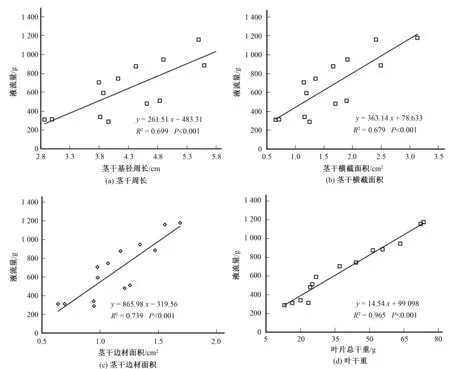
图2 柽柳日液流量与茎干周长、横截面积、边材面积及叶干重的关系
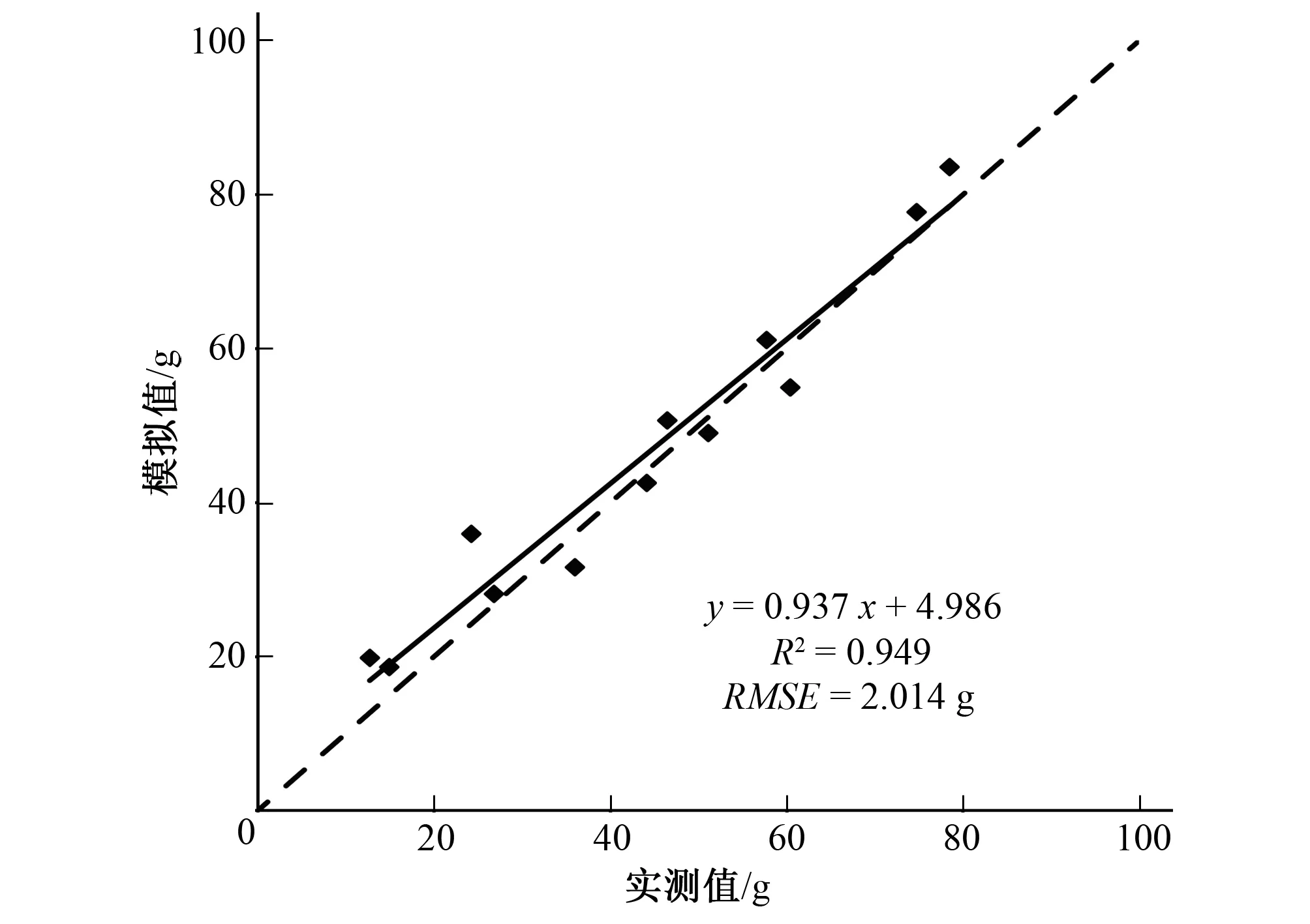
图3 柽柳单枝叶片总干重实测值与模拟值的比较(虚线表示1∶1关系)
3.2.2 柽柳单株叶片总干重回归模型
根据公式(5)计算12株柽柳的单株叶片总干重,再根据公式(6)、(7)基于冠幅周长和株高建立单株叶片总干重估算回归模型如下:
W=3.540P2H+89.877 (R2=0.938,F=182.472) (10)
为了检验模型的精度,另外选取了6株柽柳用于实测值与模拟值的误差分析,见表2。由公式(10)获得的模拟值与实测值的绝对误差介于29.036~67.741 g,误差率为11.709%~52.499%,其中植株1的误差最大,植株5的误差最小,总体表现为植株叶片总干重越小,由公式(10)模拟误差越大。可见,当样地植株叶片总干重跨度较大时,不适合用同一个公式表达单株叶片总干重与冠幅周长和株高的关系。为此,我们将植株叶片总干重划分为两个量级分别构建模型。
当W≤200 g,即P2H值小于30.3 m3时:
W=46.238 e0.049P2H(R2=0.992,F=500.921)
(11)
当W>200 g,即P2H值大于30.3 m3时:
W=379.1 ln (P2H) (R2=0.986,F=341.226)
(12)
与公式(10)模拟结果相比,由公式(11)、(12)获得的模拟值与实测值的绝对误差显著减小(表2),平均误差率分别为13.141%和8.008%,即模型精度达86.86%和91.99%,表明分级建立柽柳单株叶片总干重估算模型提高了模型估算精度。分级估测模型更符合植株叶片总干重与体积的实际关系:同一环境中,灌木体积越大,叶片总干重也越大,但当灌木冠幅增加到一定程度后,叶干重、冠幅体积随冠幅增大而增加的程度变小。
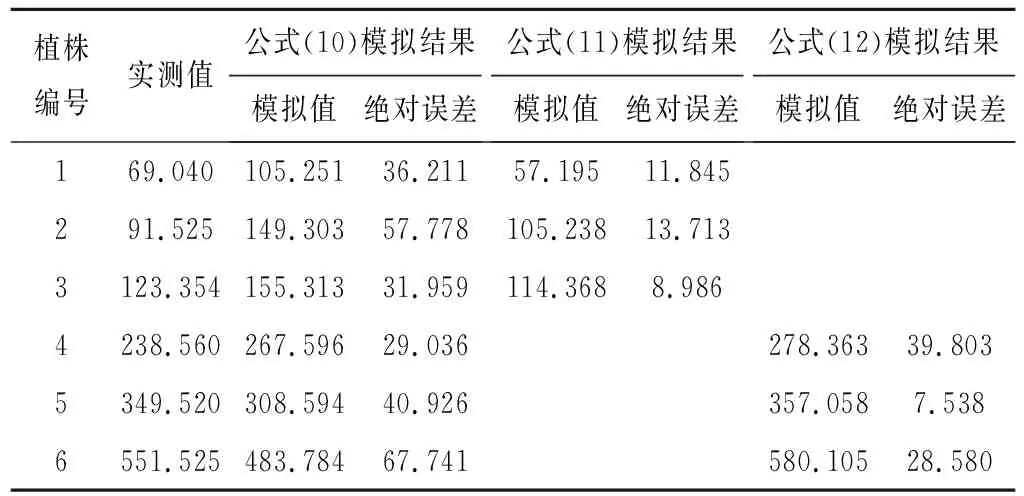
表2 柽柳单株叶片总干重实测值与模拟值比较 g
3.3 柽柳蒸腾耗水量的尺度转换
图2(d)的线性方程仅是由一天的枝条日液流量与叶干重拟合得到的。为了提高拟合的合理性,对12株样本中的15个枝条晴天时连续3 d的日液流量(7∶00-19∶00)平均值与叶干重的关系进行拟合,得到如下线性回归方程估算:
fl=14.486w+47.571 (R2=0.948,F=298.476)
(13)
式中:fl为柽柳单枝日液流量,即单枝日蒸腾耗水量,g;w为单枝叶片总干重,g。
用另外包裹着热平衡液流仪的3个枝条对公式(13)进行验证(见图4)。由图4可知茎流仪实测值与模拟值相差不大,相对误差分别为5.358%、5.929%和4.544%,平均误差为5.277%,说明用公式(13)估算柽柳单枝耗水量是可信的。
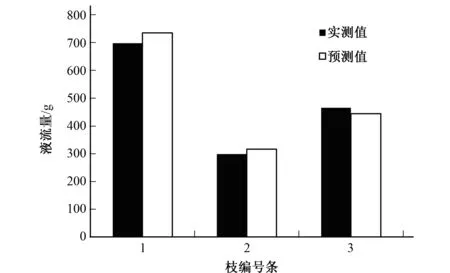
图4 柽柳3个单枝茎干日液流量实测值与模拟值的比较
借助合适的尺度转换参数可由热平衡液流仪监测的单枝耗水量来推导和获取单株、灌丛群落的耗水量。先根据公式(9)和(13)计算12株样本柽柳单株日液流量,再结合公式(11)和(12)计算每株的叶片总干重,建立柽柳单株液流量与叶片总干重之间的函数关系,其表达式为:
fl=15.605w+93.049 (R2=0.943,F=275.834)
(14)
柽柳单株耗水量线性回归方程在P<0.01水平上的相关系数R2=0.943,F=275.834,达到极显著线性相关,并且单枝耗水量估算模型[公式(13)]的估算精度在94%以上,说明利用叶干重构建柽柳单枝、单株耗水模型是可信的。
为了进一步验证柽柳单株耗水模型的可信度,随机选择3株小型柽柳样本用于检验。将同一时期柽柳单株日蒸腾耗水量模型计算的结果与快速称重法扩展获取的同株耗水量值作比较。3株柽柳各自的叶片总干重由公式(11)或(12)估算。根据公式(8),快速称重法测定的3株柽柳日蒸腾量为7∶00-19∶00蒸腾速率与叶片总干重乘积的累加值。由表3可知,两种方法的平均误差为11.657%。单因素方差分析显示两种方法测定结果的Levene方差齐性检验显著水平为0.943,远远大于0.05,说明两组测定结果在同一水平下方差一致;差异性水平为F=0.054,P=0.828>0.05,表明两种方法测定的柽柳单株耗水量之间没有显著差异,故认为用叶片总干重作为变量估算柽柳蒸腾耗水量是可行的。
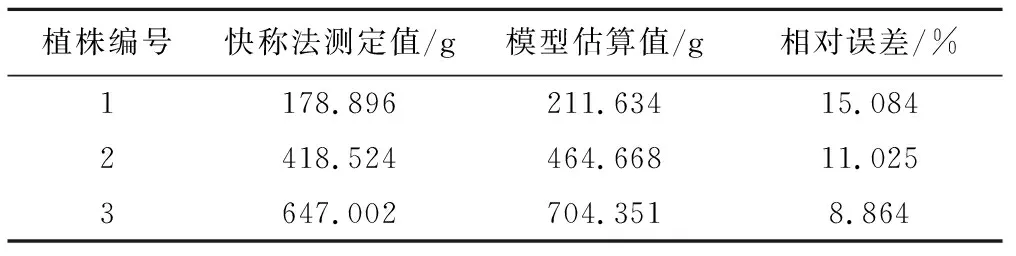
表3 两种方法测定结果的相对误差
考虑到本文的单枝/株叶片总干重是由柽柳形态参数易测因子枝条基径与长度,或植株冠幅与株高估测的,所以把公式(13)与(9)合并得公式(15),公式(14)与公式(11)、(12)分别合并得公式(16)和(17),将晴天柽柳单枝/株的耗水量回归方程转换为单枝/株耗水量与易测因子(枝条基径与长度、植株冠幅和株高)之间的关系,各表达式如下:
fl=1.072 (dh)+258.168
(15)
当PH<30.3 m3时:
fl=724.544 e0.049PH+93.049
(16)
当PH>30.3 m3时:
fl=5 915.856 ln(PH)-18 729.702
(17)
本文的研究区为退耕还林地,柽柳的行株距均为4×2 m,所以通过估算柽柳标准木的平均日蒸腾耗水量,再乘以50 m×50 m样地内柽柳的株数,即可获得样地内柽柳的日耗总量。50 m×50 m样地范围内应有338株柽柳,除去死亡的21株,实际共有317株。经计算12个标准木的日平均耗水量为5.320 kg,那么50 m×50 m样地内柽柳日耗水总量约为1 686.44 kg,即约0.675 mm,生长季5至10月的累计耗水量约124.2 mm。另外,对灌木种植布局不统一,且植株个体差异较大的小尺度样地而言,也可通过测量样地内每株植物的冠幅、株高,通过公式(16)和(17)计算出所有植株的日耗水量,再求和得到样地灌木总耗水量。
4 结 语
(1)植物生态学参数是影响植物耗水特性的主要因素之一。本文以单位时间通过横截面的液流量、单位时间通过单位横截面的液流量和单位时间单位叶干重的液流量分析了柽柳形态学参数对不同径级茎干液流的影响。无论用何种单位表示液流速率,3个茎干的液流变化趋势相同,但3种单位表示中仅经叶干重标准化处理后可以很好地消除不同枝茎干液流间的差异。同时线性回归分析表明,柽柳茎干液流与叶干重极显著相关,在P<0.001水平上相关度R2达0.965,而液流量与茎干边材面积、横截面周长和面积的相关度R2分别为0.739、0.669和0.679(P<0.001)。之所以与叶干重显著相关,是因为叶片是植物进行蒸腾作用的主要器官,叶片数量直接关系到蒸腾量,且干旱区灌木分布相对稀疏叶片之间相互遮挡度不高。
(2)以枝条基径和长度建立的柽柳单枝叶片总干重的最优模型为:w=0.074(d2h)+14.538(R2=0.902,P<0.01);以P2H=30.3 m3为分界点,利用冠幅周长与株高建立的单株柽柳叶片总干重估算模型分别为W=46.238 e0.049P2H(R2=0.992,F=500.921)和W=379.1 ln(P2H)-1 206.2(R2=0.986,F=341.226),精度分别达86.86%和91.99%。董道瑞等[20]利用冠幅周长与株高建立的塔里木河下游柽柳生物量估算模型精度为80.09%;彭守章等[22]利用相同参数建立的黑河下游柽柳生物量估算模型精度达90%以上。本文的估算模型精度明显高于前者,而与后者相似,主要是因为同一环境中,当灌木冠幅增加到一定程度后,叶干重、株高随冠幅增大而增加的程度变小,所以在建立模型时应依据灌木体积分级构建,可提高模型精度。
(3)基于叶干重的单枝、单株柽柳耗水模型均达到了显著水平,模拟值与实测值的平均误差分为为5.277%和11.657%,说明基于叶干重的柽柳耗水估算模型是可信的。结合叶干重与冠幅、株高的函数关系,单株柽柳耗水模型可表述为当P2H<30.3 m3时,fl=724.544 e0.049 P2H+93.049;当P2H>30.3 m3时,fl=5 915.856 ln(P2H)-18 729.702。根据模型估算研究区柽柳生长季5-10月的累计耗水量约124.2 mm,该值处于彭守章等[22]计算的柽柳多年平均耗水量在30~386 mm研究结果的范围内。
本文用于建立估算模型的数据为2014年6月和8月晴天时的液流数据和同时期的植物生态学参数,因此推算的柽柳生长季耗水量与实际值可能存在误差。借助热平衡液流仪可实时监测植物茎干液流变化的特点,建立植物不同生长阶段、不同天气条件下的柽柳单枝/株液流量与叶干重或者形态特征易测因子的关系,则有助于更加准确地掌握柽柳整个生长季的蒸腾耗水量的动态变化。

