基于Free Search的植被叶面积指数Logistic模型研究
朱伟峰,王 斌,杨军明
(1.黑龙江省农田水利管理中心,哈尔滨 150040;2.东北农业大学水利与土木工程学院,哈尔滨 150030)
叶面积指数(Leaf Area Index,LAI)是描述植被冠层结构的重要参数之一,控制着植被的蒸散发、截留等多种物理生物过程[1],在农业、林业、水文等学科领域应用广泛[2,3]。通常可以采用直接和间接两类方法获取植被的LAI,直接方法较精确,但工作量相对较大,部分直接方法由于采样对植被具有破坏性;间接方法能够在较短时段内获取大范围内的LAI数据,可以有效减少对植被的破坏作用,但一般需要直接方法进行校正[2-5]。然而,无论采用直接法和间接法,一般均不易获取连续短时段(如逐日)的LAI数据。
在利用遥感影像研究区域植被作用时,归一化植被指数(Normalized Difference Vegetation Index,NDVI)是描述植被生长状态和空间分布的最佳因子[1,6],也是采用间接方法反演区域LAI的常用数据[7-10]。然而,目前能够获取的NDVI多为月、旬等时段数据,基于这样的NDVI数据所反演的LAI相应地为LAI的月值和旬值;不仅如此,在农田等小空间尺度,受试验处理、人工、资金、天气等条件限制,采用取样等直接方法测定LAI时也很难做到逐日观测。另一方面,关于植被蒸散发、截留等过程的研究通常在更小的时间尺度开展,涉及的LAI往往为日等时间步长,因此,需要采取一定的方法将基于月、旬NDVI数据反演的月、旬LAI转化为较短时段序列。针对这个问题,本文以呼兰河流域为例,应用月NDVI反演了该流域6种土地覆被类型下的植被月LAI系列,同时对传统的Logistic模型进行了相应改进,提出基于自由搜索(Free Search,FS)算法识别参数的Logistic模型,并利用该模型模拟了呼兰河流域6种植被的逐日LAI,以期为模拟植被LAI的逐日变化过程提供一种新方法。
1 流域概况与月LAI反演
1.1 呼兰河流域概况
呼兰河为松花江左岸支流,发源于小兴安岭西麓,最大支流为诺敏河和通肯河,至哈尔滨市呼兰区流入松花江,本文的呼兰河流域是指呼兰河兰西水文站以上的汇水区。利用美国国家地球物理数据中心(National Geophysical Data Center of the United States,NGDC)的1km 分辨率的数字高程模型(Digital Elevation Model,DEM)识别河网并确定汇水区后,全流域共提取到12种国际地圈生物圈计划(International Geosphere-Biosphere Programme,IGBP)土地覆被类型,其中:混交林和耕地的面积很大,分别占流域总面积的39.50%和39.00%;有林草地、落叶阔叶林和落叶针叶林面积较大,分别占流域总面积的17.08%、1.77%和1.48%;其余7种土地覆被分布稀少,其面积和仅占流域总面积的1.17%。虽然常绿针叶林所占的流域面积比例很小(0.13%),但常绿针叶林为该流域内唯一一种常绿的土地覆被类型,因此,本文将混交林、耕地、有林草地、落叶阔叶林、落叶针叶林及常绿针叶林6种IGBP土地覆被作为研究对象。
1.2 月LAI反演
本文所采用的LAI利用简单生物圈模型(SiB2)反演,反演公式见式(1)~式(3)[11,12]。对于流域内不同地点的6种覆被,取相同时期(同年同月)各网格LAI的平均值作为该种覆被LAI的月份值。
(1)
(2)
(3)
式中:SR为简单植被指数;FPAR为光合有效辐射比率;FPARmin为最小光合有效辐射比率,取0.001;FPARmax为最大光合有效辐射比率,取0.950;Fcl为丛生植被比例;SRmin为5%NDVI对应的SR值,可取0.039;SRmax为98%NDVI对应SR值;LAImax为植被充分生长时的最大LAI;Fcl、NDVI98%、LAImax参考文献[7]确定。
本文采用NOAA-AVHRR的全球8 km分辨率NDVI数据集作为反演覆被LAI的基础数据,由于该数据集存在数据缺失情况,在本文的研究时段(1982-2000年)内,缺失的1994年9-12月数据利用1993年的相应月份数据代替。采用IGBP土地覆被数据识别流域内部的覆被后,利用公式(1)~(3)求得的呼兰河流域6种覆被1982-2000年间的月LAI平均值见表1。
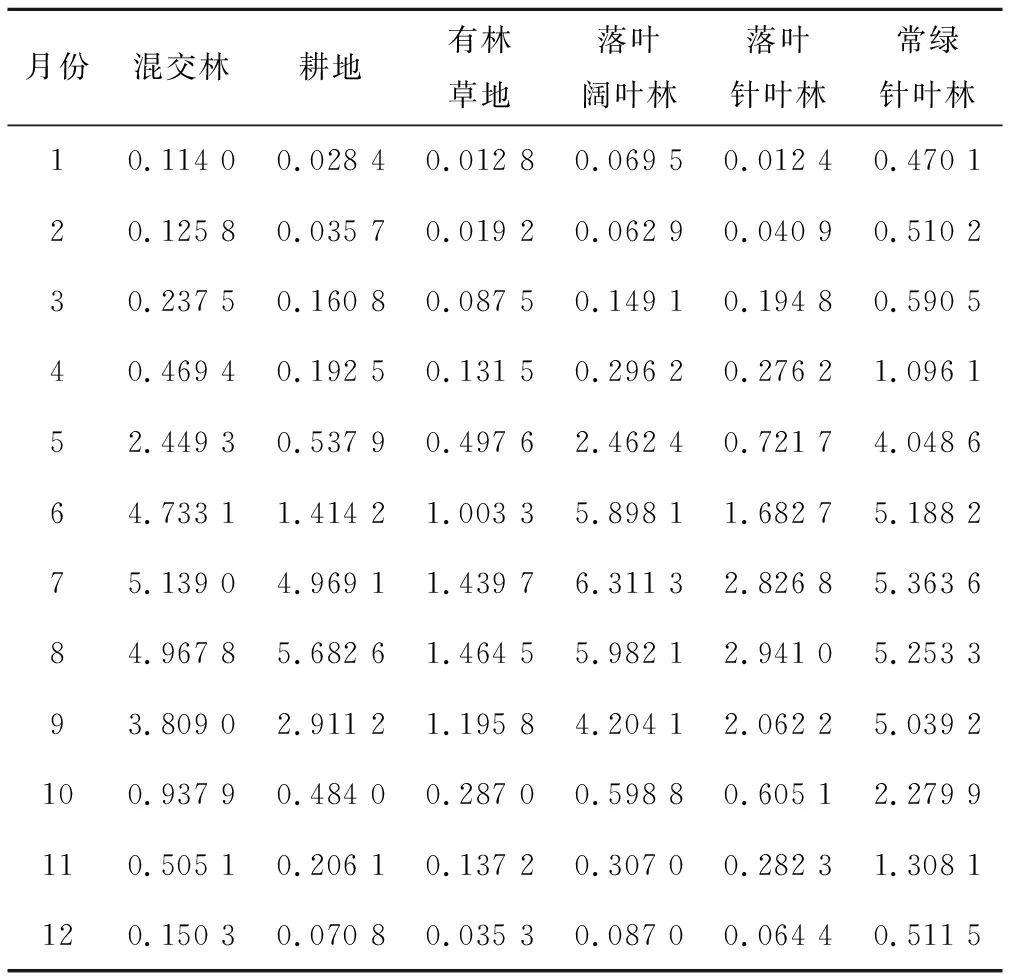
表1 呼兰河流域6种覆被多年平均叶面积指数 Tab.1 The average of leaf area index from 6 land covers of Hulan River basin
2 改进的LAI模型及其参数识别
2.1 Logistic方程及其改进模型
荷兰生物学家 Verhulst 提出的Logistic曲线可分为先缓慢增长、再快速增长、最后逐渐趋于稳定3个阶段,能够反映事物发生、发展与成熟的一般规律,又可称为生长曲线或“S”曲线,其数学方程一般可表达为[13]:
(4)
式中:t为时间;W为t时刻的变量值;Wm为W的理论上限;a、b均为待定参数。
为能更好地利用Logistic方程模拟作物干物质积累的动态过程,王信理[13]提出了2种修正的Logistic方程,并利用修正的模型模拟了作物叶、茎、穗干重的动态变化过程,模拟效果良好。其中,采用二次函数作为指数的修正Logistic模型如下:
(5)
式中:X为作物群体的状态变量;Xm为作物群体状态变量的最大值;a1、b1、c1均为待定参数。
考虑到传统Logistic方程的曲线为“S”形,而植被LAI在一年内的变化过程为单峰形,为克服传统Logistic方程在模拟年内逐日LAI时线型方面的劣势,参考式(5),提出式(6)、式(7)2种改进的Logistic模型,其中式(6)的3参数模型与文献[13]一致,记为模型Ⅰ;式(7)的5参数模型为改进模型,记为模型Ⅱ。模型Ⅰ和模型Ⅱ均取日序数的相对值作为时间变量,为了保证能够模拟平、闰年内所有日期的LAI,年最大日序数取为366。
(6)
(7)
式中:J为日序数,J=1,2,…,366;LAIj为第j日的植被LAI;p1、p2、p3、p4、p5均为待定参数。
2.2 叶面积指数Logistic模型参数识别
式(6)和式(7)含有较多的参数,普通的方法难以奏效,本文将自由搜索(Free Search,FS)算法[14]引入到改进模型的参数率定中,以期提供一种不过多依赖专业经验,但效率和精度均较高的逐日LAI模拟模型参数识别方法。
采用FS率定Logistic模型参数时,设动物群体数量为m,则动物个体每步探查行走的位置向量对应参数的一组潜在解。第j个动物通过T步探查行走得到的位置矩阵可表示为:
(8)
式中:t为探查步伐数,t=1,2,…,T;Pj为第j个动物T步探查得到的位置矩阵,j=1,2,…,m;ptj为第j个动物第t步探查时的位置向量;ptij为第j个动物第t步探查时的第i维位置分量(即改进Logistic模型的第i个参数),i=1,2,…,n,本文模型Ⅰ中n=3,模型Ⅱ中n=5。
采用随机化的初始策略,则:
p0ij=pimin+(pimax-pimin)rand(0,1)
(9)
式中:p0ij为第i维位置变量的初始值,即Logistic模型第i个参数的初始值;pimin、pimax为第i维搜索空间的边界,即Logistic模型第i个参数值的变化区间;rand(0,1) 为介于[0,1]之间的随机数。
通过探查行走,更新动物个体位置:
ptij=p0ij-Δptij+2Δptijrand(0,1)
(10)
式中:Δptij=Rij(pimax-pimin)rand(0,1),Rij为搜索邻域半径。
在探查行走过程中,动物个体的行为可以表示为:
ftj=f(ptij)fj=max (fij)
(11)
式中:ftj为第j个动物第t步探查所得的目标函数值;fj为第j个动物t步探查过程中的最优值;
信息素Ij更新为:
Ij=fj/max (fj)
(12)
敏感性Sj更新为:
Sj=Smin+ΔSj
(13)
ΔSj=(Smax-Smin)rand(0,1)
(14)
式中:Smax为最大敏感性;Smin为最小敏感性。
Imax=SmaxImin=Smin
(15)
最后,选择和决策下一次探查行走的开始位置:
(16)
式中:Il为第l个动物散发的信息素。
采用式(17)的均方误差(Mean Squared Error,MSE)作为FS识别参数的优化目标函数,并以式(17)评价模型的模拟精度:
(17)
式中:N为月份数,N=1,2,…,12;LAIinv,N为利用NDVI反演的LAI;LAIsim,N为模型Ⅰ或模型Ⅱ模拟的LAI。
由于本文识别模型参数采用的LAI为月值,而模型Ⅰ和模型Ⅱ模拟输出的LAI为日值,因此,对于6种土地覆被,在式(17)中,取每月第15日的LAI模拟值对应NDVI反演的月LAI。
3 结果分析
利用FS率定的模型参数及模型模拟均方误差见表2,2种模型对6种土地覆被的月LAI模拟结果见图1。

表2 FS率定的2种Logistic叶面积指数模型参数及其模拟误差Tab.2 The parameters and error of two Logistic models on leaf area index calibrated by Free Search
从表2可以看出,模型Ⅰ和模型Ⅱ对6种覆被的月LAI模拟精度均较高,虽然二者的MSE相差甚微,但改进后的模型Ⅱ的MSE更低。由图1可见,模型Ⅰ和模型Ⅱ对混交林、落叶阔叶林的模拟效果良好;但2种模型对冬季各月植被LAI的模拟值均偏低,分析原因是在冬季(约为每年的11月至次年4月),除常绿针叶林外,呼兰河流域其他土地覆被类型下的植被或死亡,或落叶处于休眠期,理论上这一季节的植被LAI很小,甚至趋向于0,而利用NDVI数据、采用式(1)~式(3)估算的植被LAI值在冬季通常不会为0。此外,模型Ⅰ在夏季七八月对LAI的估计值偏低,而改进后的模型Ⅱ在夏季对植被LAI的模拟结果良好。综合表2和图1所述,本文建立的2种叶面积指数Logistic模型对月LAI的模拟结果均可以接受,相对而言,改进的模型Ⅱ的模拟效果更佳。
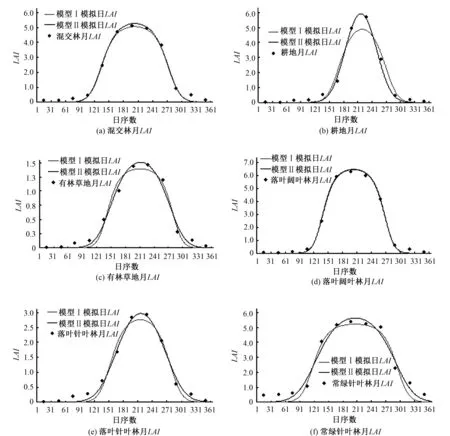
图1 两种Logistic模型对不同覆被叶面积指数的模拟结果Fig.1 Simulation result of two Logistic models on leaf area index of different land covers
4 结 语
当前,能获取的NDVI虽然空间分布情况较好,但时间分辨率仍较粗,通常为月、旬数据集,利用这样的NDVI反演的LAI时间分辨率较低,一般难于满足更短时间步长的客观需求。借鉴以往学者在研究Logistic模型时取得的成功经验,通过增加参数建立了可以模拟不同土地覆被LAI日变化过程的Logistic模型。FS算法计算过程和程序实现过程简单,不需要复杂的数学知识,也不过分依赖专业经验,以均方误差作为模拟准则,利用FS算法可以快速识别所建立的Logistic模型参数,为模拟区域不同土地覆被LAI的逐日变化过程提供了一种新途径,也可为田间尺度下,将实测不连续的植被LAI插值为更短时间步长系列提供参考。

