基于SOGI的记忆相位延迟锁相环研究

时维国, 刘晨

(大连交通大学 电气信息学院，辽宁 大连 116028)

0 引 言

随着分布式发电系统的发展，并网逆变器的应用越来越广泛[1]。在并网逆变器控制策略中，三相静止坐标系与两相旋转坐标系之间的变换会用到电网电压的相位角，因此，获取实时准确的电网电压相位角是并网逆变器实现精确控制的前提。锁相环分为开环锁相环和闭环锁相环两大类，由于开环锁相环响应速度慢，精度低，所以闭环锁相环更适合响应速度快，高精度的场合[2]。目前最常用的锁相环技术是基于同步旋转参考坐标系的锁相环[3](Synchronous Rotating Frame Phase Locked Loop,简称SRF-PLL)。但是电网出现不平衡电压时，锁相环输出相位波动，相位差出现两倍频的较大脉动[4-6]。近年来，很多学者采用特定的滤波技术对不平衡电网电压进行正负序分离，然后对正序分量(Positive-Sequence Component,简称PSC)进行提取。文献[7]提出基于全通滤波器的锁相方法，但是，当电网含有谐波时，该方法的锁相误差变大。文献[8]提出了基于双二阶广义积分的锁相环DSOGI-PLL(double second order generalized integrator-PLL)，但是由于信号调理电路可能会引起直流偏置，所以会造成锁相精度的下降。文献[9-11]是在SRF-PLL中的Park变换后且在PI控制之前，通过d轴分量进行滤波(陷波)等处理，消除二倍频以及其他低频分量，进而得到准确的相位信息。考虑到有些场合需要锁相算法简洁以及系统延时小等因素，该方法不再适应。

本文提出基于二阶广义积分的电压信号延迟的新的电网电压正负序提取和分离方法，仿真试验证明，该锁相环在电网不平衡电压、谐波电压及频率变化下，仍然具有高精度的锁相性能。

1 DSOGI-PLL简介及问题

当电网发生不平衡故障时，电网会存在不平衡电压，可以表示为[12]：

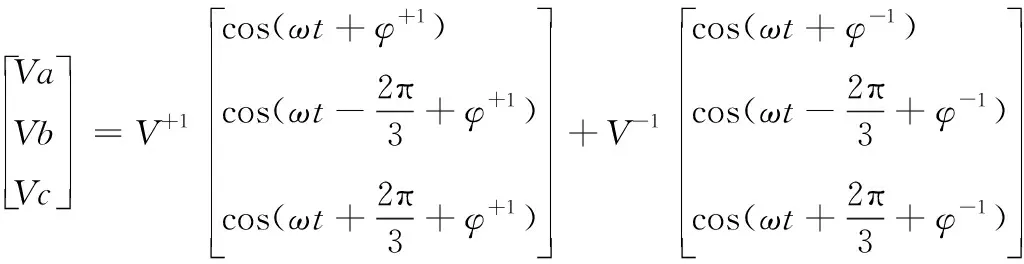
式中:“+1”和“-1”分别表示电网电压的正序分量和负序分量，由于零序分量在clark变换时被消除，所以不考虑零序分量。

同时，电网电压会存在5次，7次以及更高次谐波问题[13-14]，如式(2)所示：

(2)

当电网电压发生故障时，SPF-PLL的锁相性能较差。针对该问题，很多学者做了改进。DSOGI-PLL就是其中之一。图 1为DSOGI-PLL锁相环原理框图。

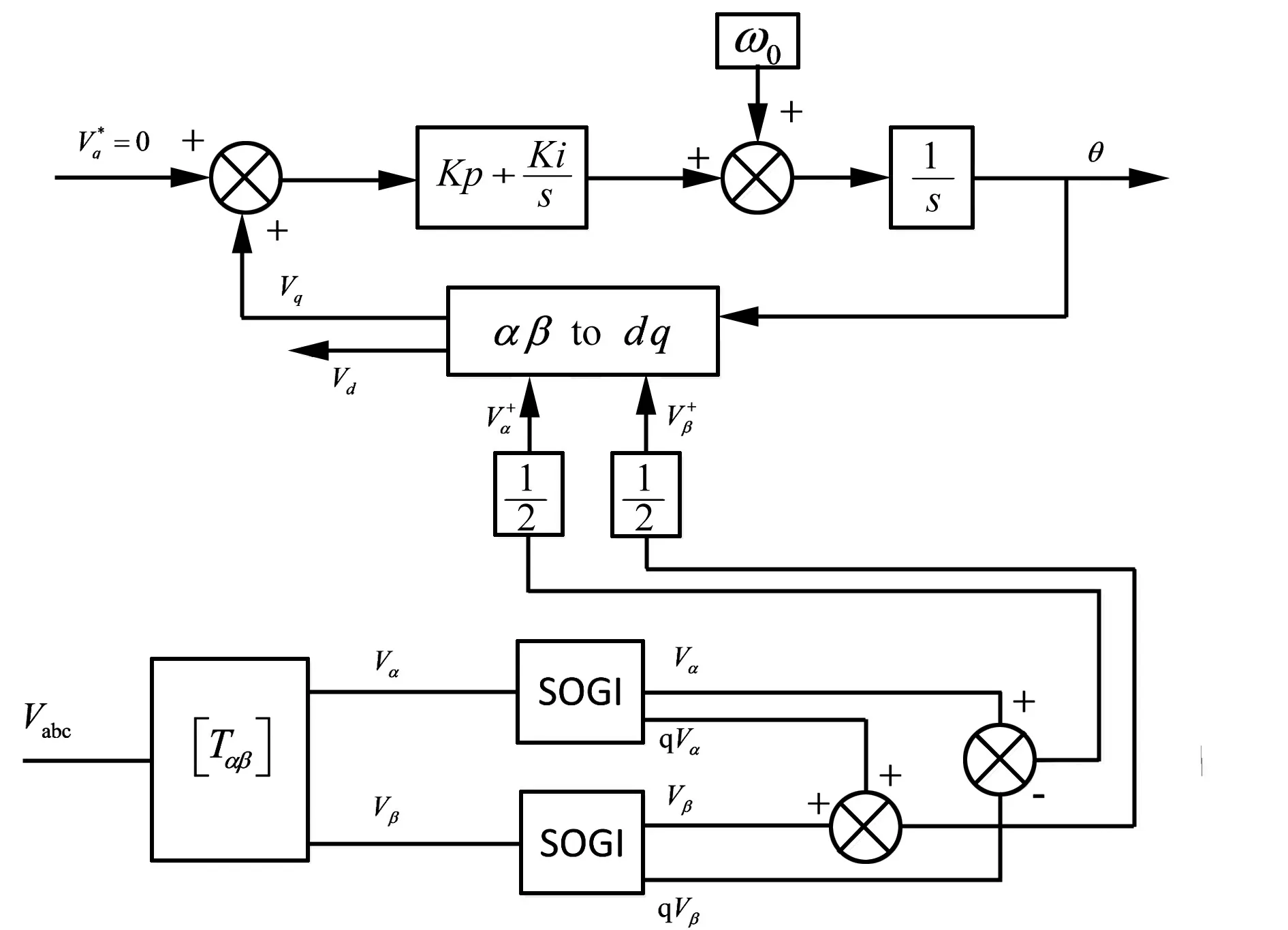
图1 DSOGI-PLL锁相环原理图

在DSOGI-PLL中，DSOGI对电网电压正序分量进行提取和滤波。其滤波器的传递函数为：

(3)

图2、图3为D(s)，Q(s)的bode图。由图2、图3可知,D(s)为带通滤波器，当ω0=ω时，输入信号可以无衰减地通过，在其他频率处输入信号均有不同程度地衰减，k值越小，衰减程度越大，相应的带宽也越小，对直流分量的抑制能力也越强，调节时间越长，工程中可以根据实际要求选择合适的k值，Q(s)为低通滤波器。

图2 D(s)滤波器bode图

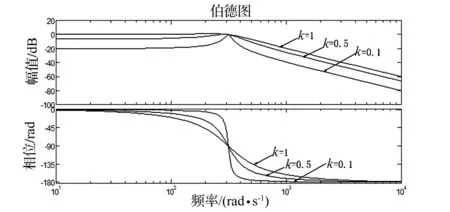
图3 Q(s)滤波器bode图

当电网电压存在直流分量时，经过D(s)滤波器的直流分量基本都可以衰减掉，而经过Q(s)滤波器的直流分量的衰减特性则与k值的选取有关。k值越小，直流分量的衰减度越高，但是仍然存在。因此当电网电压存在直流偏置时，DSOGI无法消除直流分量引起的误差[15]。

2 改进型锁相环

为了解决此问题，只使用D(s)滤波器来滤掉电网电压中存在的高次谐波及直流分量。

由上述可知，D(s)滤波器对直流分量和高次谐波有很大的衰减，谐波次数越高，衰减越大。不平衡电压信号通过D(s)滤波器滤波后，将只剩下基波电压的正负序分量。然后通过以下方法去除负序分量。

经过park变换后得到的d，q轴电压vde，vqe可以表示为：

(4)

在d，q旋转坐标系下，PI控制系统将控制旋转角度，实现锁相误差Δθ=ωt-θe为0的目标。因此，在理想状况下ωt=θe，在d，q旋转坐标系下式(4)可表示为：

(5)

由式(5)可以看出，在d，q旋转坐标系下的锁相系统中，三相电压的正序分量变为了直流量，而三相电压的负序分量变为了电网电压频率的两倍。

本文是通过在α，β坐标系下，将电压信号延迟π/4角度来消除负序分量的。

理想状况下，α,β坐标系电网电压可表示为：

(6)

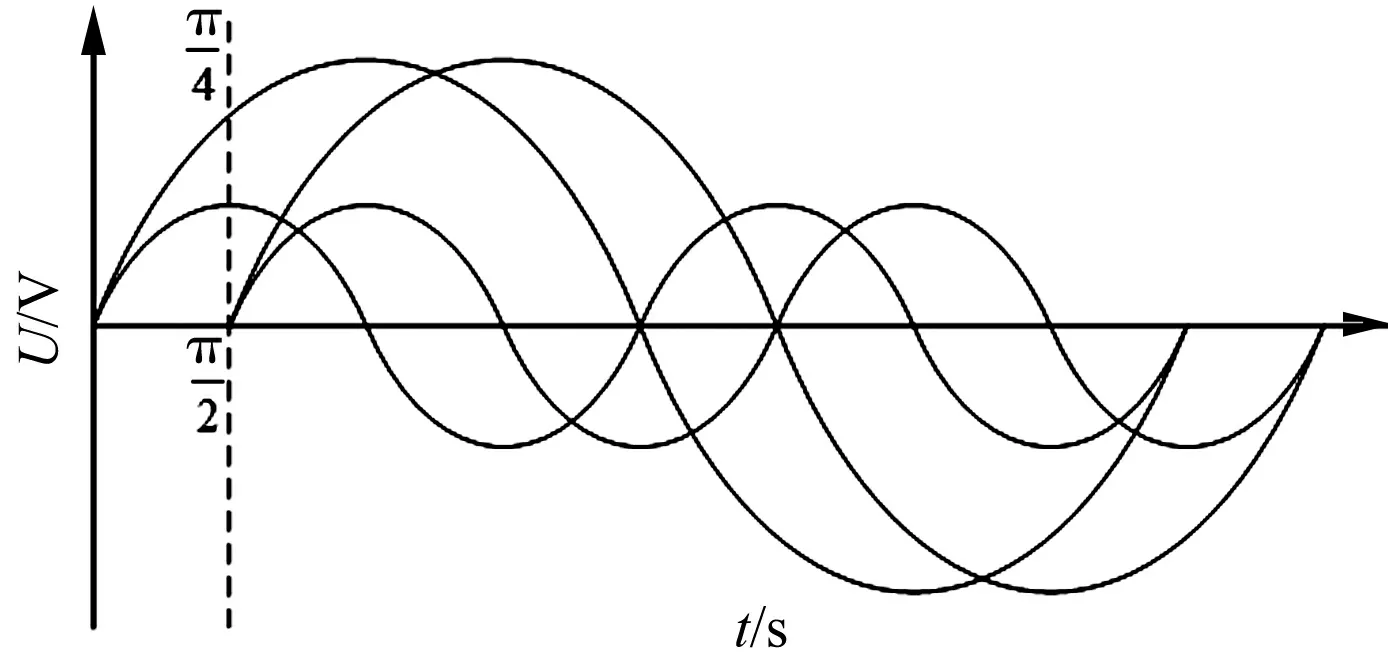
图4 电压信号延迟原理图

将ωt=(θ-π/4)代入式(6)中，在α，β坐标系下，电网电压信号延迟了π/4的相位。在d，q旋转坐标系下，负序分量相当于延迟了的π/4相位，如图4所示。

化简后得到d，q轴下含负序分量的电压如式(7)所示：

(7)

将延迟后的d，q轴电压信号与延迟前的d，q轴电压信号经过简单的加减混合运算即可提取出正序分量。计算公式如式(8)所示。

(8)

电网电压正序分量提取结构如图5所示。

图5 正序分量提取结构图

电网电压信号先经过二阶广义积分D(s)滤波器滤除电网电压的高次谐波及直流分量，然后经过信号延迟和坐标变换模块，最后经过加减混合运算将基频电压中的负序分量去除。

图6为二阶广义积分D(s)滤波器的原理图，当电网电压频率发生变动时，只需要将锁相环输出的实时频率输入到ω0中即可完成频率的自适应性。

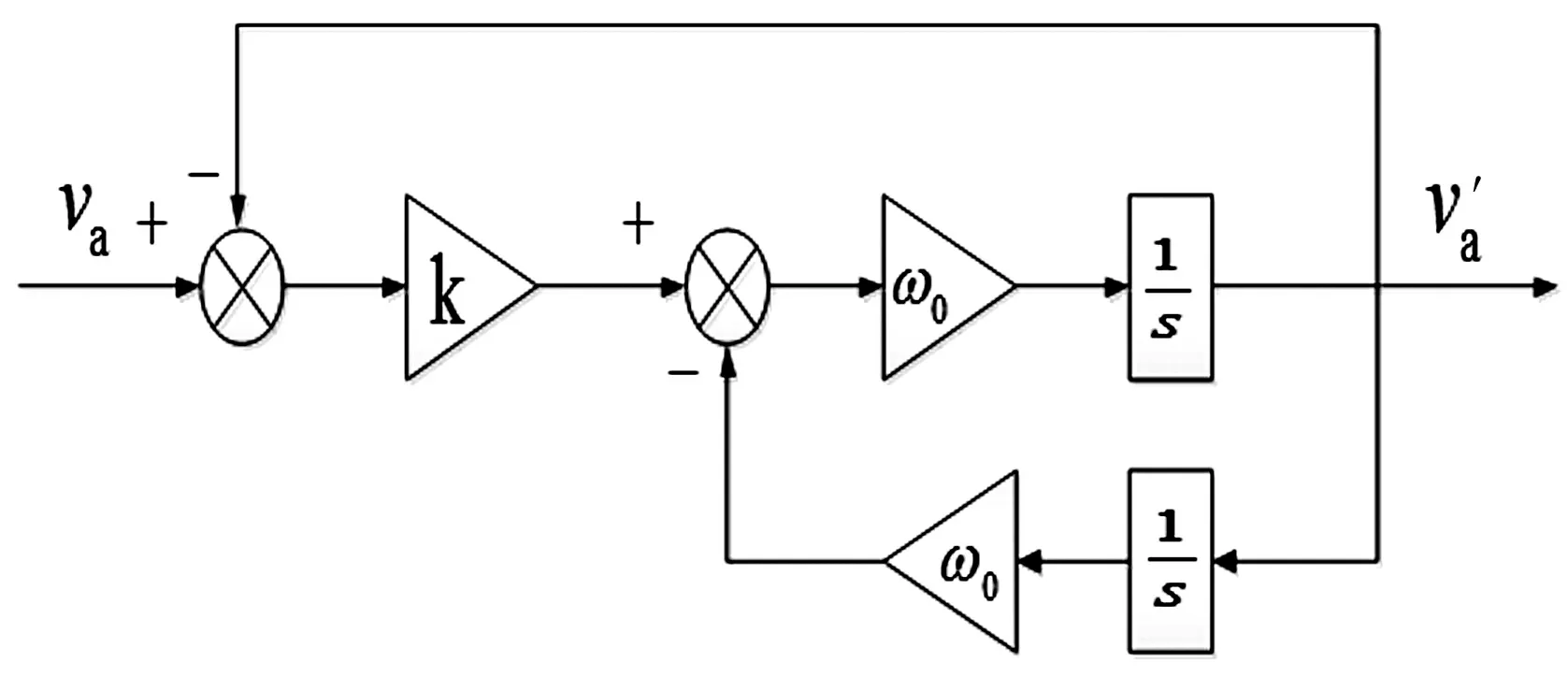
图6 D(s)滤波器原理图

值得注意的是经过二阶广义积分滤波器滤波后的电压信号幅值是由0 V逐渐增大到额定值的，经过信号延迟再进行加减混合运算时会产生误差，因此需要在电压信号上升为额定值的响应时间内将电压信号补偿致额定值。

3 仿真分析

以MATLAB/Simulink仿真工具搭建了新型锁相环的锁相系统。参数设置如下：三相电网电压380 V，频率50 Hz。

图7为电网电压平衡状态下的三相电网电压，dq轴电压以及锁相角。从图中可以看出，在0.02 s内s轴电压稳定在0 V。锁相环正确锁相。

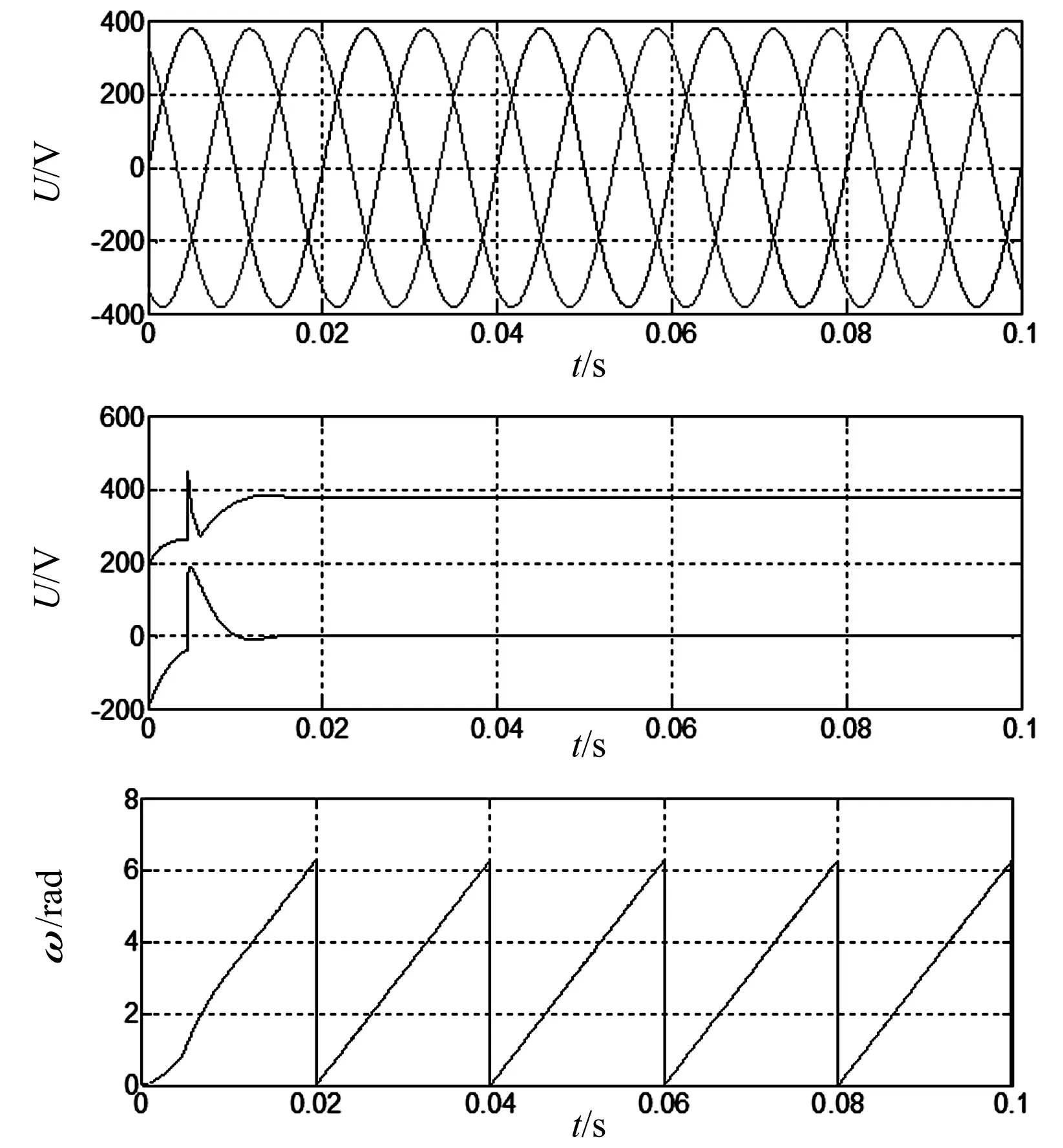
图7 平衡状态下电网电压，dq轴电压及锁相角

为了验证锁相环在不平衡电压下的锁相能力，在0.05 s处将三相电网电压的A相电压突变为原来的一半，图8为电网电压不平衡下三相电网电压、dq轴电压以及锁相角的仿真波形。从图中可以看出，在A相电网电压突变位原来的一半后，未经过加减混合运算的dq轴电压产生两倍电网电压频率的负序分量，与理论分析一致。经过加减混合运算后，q轴电压在短时间波动后迅速稳定在0 V，同时锁相环正确锁相。

图8 电压相位突变下电网电压dq电压及锁相角

为了验证锁相环在电网电压含少量谐波和直流分量情况下的锁相能力，0.01 s时在电网电压中加入幅值为38 V的5次谐波，7次谐波和直流分量如图9所示，以A相电压为例，滤波前，A相电压5次，7次谐波及直流分量含量为14.13%，滤波后谐波及直流分量含量只有0.26%。同时q轴电压仅含有非常少的5次谐波，锁相环正确锁相。

图9 谐波电压下的锁相环仿真图

为了验证锁相环的频率响应，0.01 s时将三相电网电压频率由50 Hz突变为40 Hz。从图10可以看出q轴电压在短暂的波动后很快稳定在0 V。同时角频率ω在很短时间内由100 π变为了80 π，锁相环正确锁相。

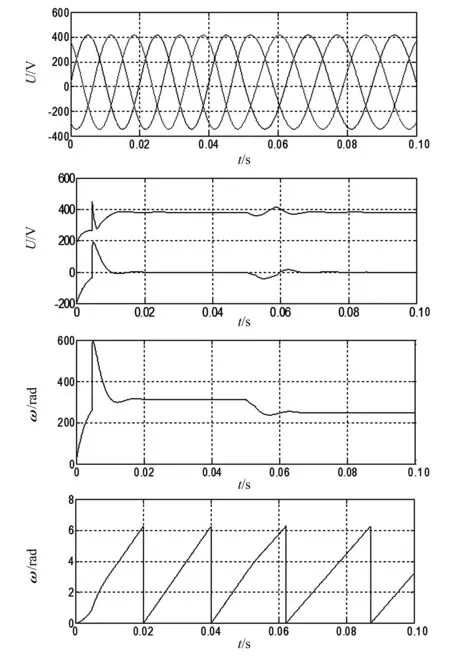
图10 频率突变下的锁相环仿真图

4 结束语

针对传统SRF-PLL在电网电压故障情况下锁相精度差的缺陷，提出了一种由二阶广义积分和记忆相位延迟相结合的电压基频信号的正负序分量提取和分离方法，该方法解决了双二阶广义积分Q(s)滤波器引起的直流偏置问题。最后，仿真结果证明，此方法同时具有在不平衡电压，谐波电压及频率突变的情况下仍能正确锁相的特点。