设境追问,让练习更高效
江苏南京市浦口区行知小学(211800) 唐兴友
在日常教学中,学生普遍表现出对练习主观淡漠、情感懈怠等不积极反应。如何才能拨动学生想要探究练习的欲望,实现练习的高效性?经过实验和摸索,笔者发现,学生喜欢的练习都有良好的练习情境和优质的练习追问这两个要素。为学生创设良好的练习情境,能够引发学生自主探索的欲望,而优质的练习追问,能够激发学生的探究热情,使学生的思维获得生长。
一、设比较之境,追问异同
有比较才有鉴别,通过比较可以知道相同点和不同点,对事物本质有更深刻的了解。在练习中,教师可以创设比较情境,追问异同,引导学生进行有条理的思考,辨析数学概念,由表象推及本质,使学生对数学知识有更深刻的理解。
比如,在教学“列方程解稍复杂的百分数实际问题”时,教师以学生的比较心为出发点设计了三组练习。
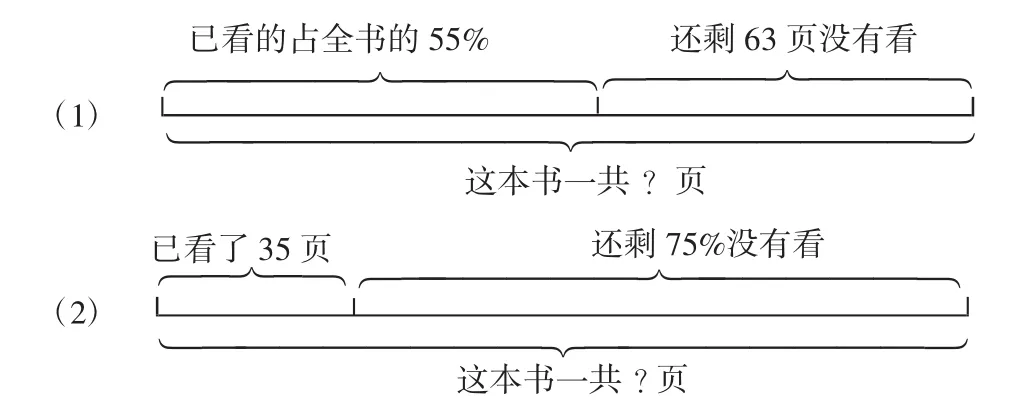
1.如图,这两题都用到了以下数量关系:已看的页数+还没看的页数=书的总页数;书的总页数-已看的页数=还没看的页数;书的总页数-还没看的页数=已看的页数。在列方程时,你会选用哪个数量关系?为什么?设置这组比较性练习,目的是让学生学会根据题意,选择恰当的数量关系列方程。
2.(1)一桶油,用去25%,正好用去2.5千克。这桶油重多少千克?
(2)一桶油,用去25%,还剩7.5千克。这桶油重多少千克?
待学生解答后,教师追问:“为什么这两道题都可以用列方程来解答?题(2)比题(1)复杂在哪里?为什么?”这组练习题的设境追问,目的是让学生思考已知量之间是否存在着直接的对应关系,由此突破教学的重点和难点。
3.(1)学校买来篮球和足球共80个,其中篮球占45%,其余的是足球。买的足球有多少个?
(2)学校买来一些篮球和足球,其中篮球占45%,足球有44个。买的篮球和足球一共有多少个?
待学生解答后,教师追问:“这两道题有什么不同点?为什么题(1)不用方程来解?”设置这组练习,目的是帮助学生进一步厘清单位1的量,找到已知和未知的关系,从而有效突破教学难点。
以上三组练习,从不同角度层层追问,步步深入,通过比较情境的设置及多次的追问异同,引发了学生的自主比较,借助比较使学生更好地关注问题的核心,更透彻地理解数学知识和数学概念。
二、设互助之境,追问算理
每个学生的内心都存在沟通、交流、合作的交往需求,教师可依据学生的年龄特点创设互助情境,让学生借助同伴合作的机会和教师的追问,深刻理解算法和算理。
比如,在教学“小数乘小数”时,为了能让学生对枯燥乏味的数学运算练习感兴趣,教师紧紧围绕互助互学创设了三组练习情境,并展开层层追问。
1.互相推荐
教师出示练习:(1)1.6×24;(2)9×5.4;(3)1.38×2;(4)4.1×30;(5)72×0.66;(6)1.45×12。这些练习可帮助学生复习巩固整数乘一位小数。待学生思考后,教师追问:“如果只需做其中两道题,那么你认为哪两道题比较合适帮助大家复习呢?”这立刻引发了学生的踊跃发言,通过分组讨论后,最终选出了题(1)和题(6)。这两道题既体现了练习的梯度,又迁移了整数与小数相乘的计算法则,在帮助学生回顾整理旧知的同时,也为新知做好了铺垫。而从学生心理上来说,由原来要做六题降低为只需做两题,内心获得了满足感和兴奋感。
2.互相设计
为了充分调动学生的能动性,教师可以让学生尝试设计三道小数乘小数的练习题,并说出理由。学生积极思考之后,设计出的习题有的难易层次比较明晰,比如7.5×2.3,7.8×0.78,6.5×3.4;有的计算量比较大,比如3.55×2.33,9.11×2.22,1.13×2.2。通过互相设计习题,满足了学生的表现欲,学生竭尽全力设计出的难题,不但考验了同伴,同时也是考验自己,有效提升学生对知识的综合运用能力。
3.互相诊断
“爱找茬”是学生的童趣所在。为此,教师设计习题:“小明的妈妈计算8.6×3.2,结果等于23.4。你认为这个答案正确吗?为什么?”学生立刻表现出了极大的兴趣,七嘴八舌的开始纠错。教师乘胜追击,呈现小明纠错后的口算方法(如下图),并追问:“你认为小明的算法对吗?为什么?”

通过互相诊断的练习,不但丰富了学生检验算法的途径,而且将竖式计算和图形相结合,再一次帮助学生厘清了小数乘整数的算理。
三、设探究之境,追问数形
在教学中,通过课堂探究能够发现新问题,得出新思考。对于学生来说,猎奇探究也是一大认知喜好,因此,教师可以为学生创设具有探究情境的练习,利用数形结合追问学生,使要研究的问题化难为易,步步深入。
比如,教学“分数的初步认识”时,为了让学生更好地掌握和理解分数的概念,教师设计了三组探究练习。
1.探究分数意义
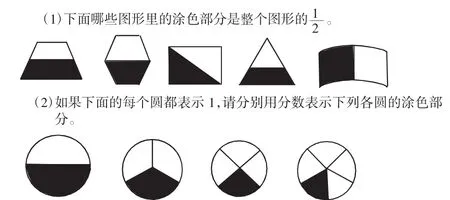
待学生解答后,教师追问:“从这些图中你明白了什么?仔细观察这些分数,它们有什么相同的地方?”
通过这组探究练习,学生感悟到不管把一个圆等分成多少份,涂色的部分都表示等分的几份中的一份。
2.探究分数大小
教师结合上图,让学生比较同一个圆的1/2、1/3、1/4和1/5的大小,并追问:“按顺序观察,你发现了什么?”学生通过观察比较,发现同一个圆等分的份数越多,它的每一份就越小。
3.探究数学思想方法
教师设计探究练习:“如果把 1/2,1/3,1/4,1/5……在分数条上表示出来,你会发现什么?”待学生解答后,教师追问:“1/10有多大,1/5又有多大呢?”通过探究练习和追问,让学生在头脑中建立起一个分数墙,充分体会到分母越大,分数越小。
以上三组练习,逐步渗透了数形结合的思想方法,学生不仅直观感知了分数之间的大小关系,而且深切体会到分数的无限性,让函数这个概念在不知不觉中萌芽。
总之,教师应从学生的喜好出发,为学生创设特定的练习情境,设计有效追问,只有这样才能够让学生想做、爱做,最终实现练习的高效性。

