丰富找的经验,巩固找的规律
——“搭配的规律”的教学实践与反思
福建安溪县第五小学(362400) 钟夏苏
“找规律”的知识能培养学生观察、归纳的能力。那么教学时,如何展现“找”的经过,积淀“找”的经验,增强学生“找”到规律的能力呢?本文将以寻找“搭配的规律”为例谈一谈“找”的艺术。
一、强调有序思考,摸索找的捷径
师:同学们到麦当劳点餐,一般吃什么套餐?(学生自由交流)快餐店提供了牛肉汉堡、薯条、鸡翅3种熟食以及可乐、柠檬汁2种饮品,如果选1种熟食和1种饮料做早餐,你准备如何配餐?(学生自由回答)
师:看来配餐方式多种多样,那共有几种配餐方案呢?(大部分学生回答有6种)
1.合作探究证明:到底是不是6种方案呢?我让各学习小组拿出事先分发的熟食、饮品图卡进行摆一摆的活动,验证一下。
2.展示汇报:学生演示搭配的过程。
(先演示随机搭配法,再演示有序搭配法)
3.小结:有序搭配,才能做到不重不漏。那么怎么做才叫有序呢?这个秩序指的是什么?
生:先选定一种熟食,再依次与所有的饮品搭配;也可先选定一种饮品,再依次与所有的熟食搭配。
数学教学的核心目标,就是要锻炼学生的数学思维能力,而有序思考恰好是数学思维严谨性的体现,也是解决基本应用问题的通法。让学生通过“有序”和“无序”两种操作方法,将“有序”从理论认识落实到具体的操作程序上,强调了有序思考,引导学生总结出搭配的规律。
二、经历探究过程,优化学习策略
让学生收起图卡,提问:如果撤走代表实物的图卡,你能用写一写、画一画、连一连的方法推演出不同的搭配法吗?请试一试。
1.学生独立试探,教师视导。
2.交流评价。
(1)展出生1的作品(文字连线表示):
汉堡—可乐、汉堡—柠檬汁、薯条—可乐、薯条—柠檬汁、鸡翅—可乐、鸡翅—柠檬汁
(2)展出生2的作品(代数符号表示):
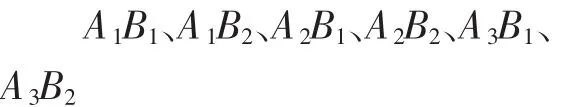
(3)展出生3的作品(连线表示,如图 1):
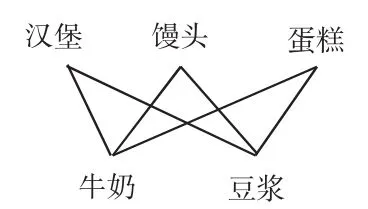
图1
(4)展出生4的作品(符号连线表示,如图2):
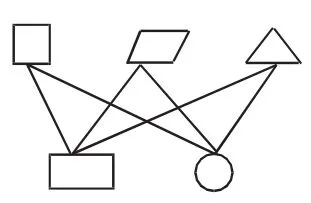
图2
有序操作让学生摸到了找规律的门道,但每次寻求搭配次序不可能都建立在操作上,因此要让学生对规律进行总结升华。这个总结升华的过程并非直接出示课本上的抽象图,而是要让学生充分探究后,在分享交流、比较优化的基础上,形成成熟可靠的思维模式。当学生解决的时候,就能按照思维的抽象展现,这样有利于思维逐步提升。
三、着眼于理解,抽象出数字计算法
1.算式表示:在前面分析总结的基础上,你能计算出配餐种数吗?(3×2=6或 2×3=6)
师:算理是什么?
生:第一个算式:依次拿3种熟食配2种饮品,即3个2种,共计6种;第二个算式:依次拿2种饮品搭配3种熟食,那3个3种,合计6种。
2.假如饮料品种增加到3种,配餐方案有多少种?
3.该如何连线?怎么计算?
生:多出一种饮品,也就意味着所有的熟食多出一种搭配模式,现在是3个3种,就是3×3=9(种)。
3.假如熟食再增加一种,有多少种配餐方案?
生:新加的熟食,又可以分别与3种饮品搭配,又多出3种匹配种类,因此就有4个3种,4×3=12(种)。
4.假如有10种熟食、8种饮品,搭配方案又有几种?
……
寻找普遍规律本质上就是建模,小学数学知识的结论很难通过理论去证明,往往是从形象直观的数学模型中抽象归纳出的。列式很简单,就是种类数乘以种类数,但如果不将搭配的思考过程用乘法概括出意义来,那数字计算规律就是死板的教条。设计增加熟食和饮品种数环节来推算搭配方案的细微变化,使计算原理得到更深的渗透。
总之,当学生通过操作、提炼、总结对规律形成客观稳定的认识后,他们的操作经验也会得到长久地发展,而对蕴藏在搭配方案中的规律价值也能得到理解上的升华。

