理解算理才能提高计算技能
江苏徐州市贾汪区紫庄镇中心小学(221133) 孙 玲
算理和算术是相辅相成的,只有主导思想和操作技能高度合一,才能做到算无遗策。下面笔者结合教学实践来谈谈讲授算理的策略。
一、立足起点,回归本源
【案例1】小数加减法
笔者先导入整数加法算式“475+2”,通过问题:“2与哪个数字相加?为什么是和5相加?”让学生回顾“相同数位对齐”的定律;然后将题目更改为“4.75+0.2”,让学生尝试计算,并探究其计算法则;在学生讨论交流了小数加法法则后,笔者再让学生比较“475+2”和“4.75+0.2”的竖式,启发学生思考:“475+2”中的2和5对齐遵循的是末位对齐的规则,而“4.75+0.2”遵循的是小数点对齐的规则,虽然这两者规则不一,但有没有相同点?
学习小数加减法之前,学生对整数加减法的计算经验十分丰富,对“末位对齐”的规则也烂熟于心,也认识到“末位对齐”实际上就是以末位为基准实现所有数位对齐。但“末位对齐”的刻板印象也会产生负迁移,在教学小数时,需要激活并提取“数位对齐才能相加减”的通则。上例中将整数加法设为知识原点,把整数运算中的“末位对齐”与小数运算中的“小数点对齐”统一起来,总结出“加减法计算要对齐数位”的通则。小数计算时,只要将计量单位替换成计数单位,然后进行类比迁移,就能得出“单位相同的数可以直接相加减,单位不一致的数需要化为单位一致才能计算”的结论。
二、建立表象支撑,倡导多元化表征
【案例2】除数是整十数的笔算
面对除数是整十数的除法,学生受到“除数是一位数除法”的影响,经常出现下列错误:
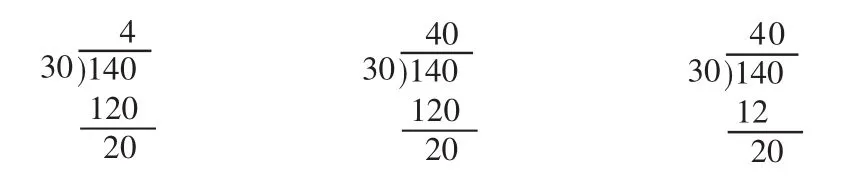
怎样纠正学生的定式思维,让学生理性对待除数变为30后商4的位置变化以及竖式中各数字所占位置的原理,这些问题都是教师要思考的。在教学时,笔者就借助拆分小棒来揭示该算式的算理。
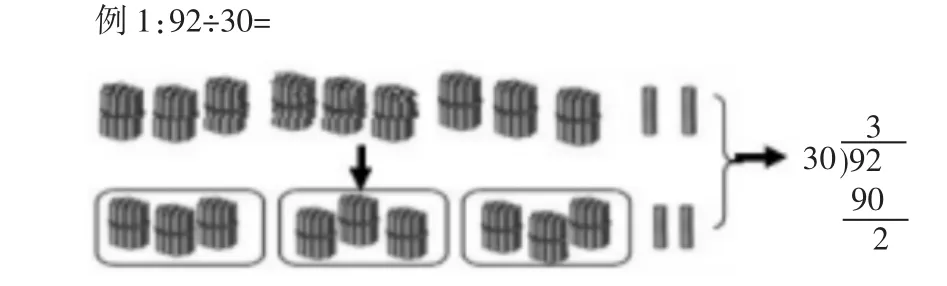
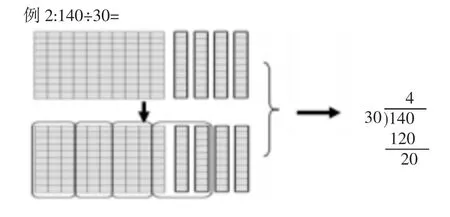
学生通过分配小棒的模型来理解竖式的意义:商代表小棒的堆数,被除数代表小棒的总数,除数代表一堆小棒的数量,很显然,分出的堆数是一位数,应该放在个位上。
三、创设问题情境,突出内涵本质
【案例3】除数是两位数的除法(试商、调商)
笔者创设问题情境:若只买其中一种魔方,153元可以买几个?

1.选购单价为21元的魔方,列式“153÷21=”
(1)怎么试商?开始试商时如何推定数位?
(2)根据情境解释为什么一开始不能在百位和十位上试商。
2.以另外两种单价为例,列式“153÷32=”“153÷38=”
(1)怎么试商?开始试商时如何推定数位?
(2)根据情境解释为什么一开始不能在百位和十位上试商。
(3)对比算式“153÷32”和“153÷38”,它们有什么不同点?为什么除数都是三十几,“153÷32”第一次试商会扩大化,而“153÷38”第一次试商会缩小化?
将除数“四舍五入”是基本的试商方法,但“四舍”时商会偏大,“五入”时商会偏小,而引入购物情境便可以很好地揭示调试上商的规则。
总之,要想促进学生计算技能的提升,教师在教学计算时就必须向学生渗透算理,加强学生对算理的理解,以确保学生的计算技能得到有效发展。

