浅谈小学生思维能力的培养与发展
福建泉州市安溪县感德镇岐阳小学(362413) 陈世军
《义务教育数学课程标准(2011版)》提出:小学数学教学实质上是思维活动的教学,摒弃思维活动的教学就不算是数学教学,更谈不上锻造思维能力,启迪智慧。教师在教学过程中应该怎样培养和发展学生的思维能力呢?对此,笔者结合平时的教学经验谈几点看法。
一、机械解题灵活化
在解决问题的过程中,学生若只是用生硬机械的解题思路去分析问题,通常把握不了解决问题的方向,这时教师引导学生摆脱死板的思维方式,调整分析问题的角度,就能拓宽学生的解题思路,使问题变得明晰。
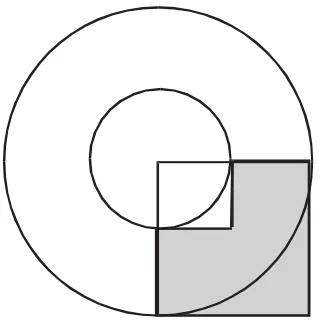
题目:如下图所示,已知圆环面积S环,求图中阴影部分的面积S阴影。
学生从图形中可以看出阴影部分的面积等于两个正方形的面积差,即 S阴影=S大正方形-S小正方形=R2-r2,但最大的问题是两个半径R和r是未知数,故不能直接将R和r代入公式求出结果。笔者是这样引导学生思考:题中已知圆环的面积S环,而圆环的面积为S环=πR2-πr2=π(R2-r2)。这时,思维灵活的学生就能发现R2-r2=S环÷π,(R2-r2)的值正好是所求阴影部分的面积,也就是不用知道R和r的值也可以解决此题。
二、抽象知识形象化
在小学数学教学中,教师若能强化数学知识与其他知识的横向联系,那么不仅能拓宽学生的思维,而且能使抽象的知识形象化和具体化。
例如,新人教版四年级下册数学广角中的“鸡兔同笼”问题:笼子里有鸡和兔子,已知共有45个头,116只脚,问笼子里鸡、兔子各有多少只?其实,这道题的难点是鸡和兔子的脚的只数不同,假如鸡和兔子的脚数相同,那么解决这个问题就变得简单多了。在教学时,笔者设置了一个课堂游戏,对学生下令:“假如你们都是兔子。全体兔子立正!提起前两只脚。”(通过多媒体展示兔子的抬脚过程)笔者接着说:“现在每只兔子和每只鸡的脚的数量一样了,有45个头,脚的总数有什么变化呢?”学生顿时明白:缺少的26只脚是兔子提起来的前两只脚。通过游戏,学生很快领会了解决问题的方法和策略。
三、发散思维多样化
在教学过程中,教师要引导学生挖掘并处理教材中有价值的素材,同时启发学生从多角度思考问题,把握全局,进而提高学生解决问题的能力。例如,题目:学校为补充体育室的器材,购买了一条长135米的尼龙绳,已知先剪下9米做了5根跳绳,照这样计算,剩下的尼龙绳可以再做几根这样的跳绳?
(1)利用“直进归一法”思考:先求每米可以做多少根跳绳——(5÷9),再求其他数量。列式:(5÷9)×(135-9)。
(2)利用“逆转归一法”思考:先求每根需要多少米——(9÷5),再求其他数量。列式:(135-9)÷(9÷5)。
(3)利用“倍比法”思考:先求剩下的长度是剪下长度的多少倍——(135-9)÷9,再求其他数量。列式:5×[(135-9)÷9]。
(4)利用“正比例关系”思考:每根跳绳的长度不变,根数与米数成正比例。设剩下的尼龙绳可做x根这样的跳绳。列式:9∶(135-9)=5∶x。
(5)利用“等量关系”思考:剪下的长度加上剩下的长度等于总长度,设剩下的尼龙绳可做x根这样的跳绳。列式:9÷5×(5+x)=135。
四、进退结合,相辅相成收奇效
在解决问题的过程中,教师要引导学生学会把握事件发展过程的全貌,用辩证的眼光看问题,进退结合,通常可在解题时取得意想不到的效果。
例如,题目:小明今年10岁,他的妈妈今年35岁,问几年前,妈妈的年龄是小明的6倍?
先前进:已知“小明今年10岁,他的妈妈今年35岁”,可知今年他们两人的年龄差为35-10=25(岁)。
再后退:考虑目标——“几年前,妈妈的年龄是小明的6倍?”由此可以想到,那时妈妈的年龄比小明大6-1=5(倍)。解题的关键是:不管是经过几年,两人的年龄总是相差 25 岁。采用“差倍”方法求解:(35-10)÷(6-1)=5(岁)。当小明 5岁时满足题目要求,10-5=5(年),即 5年前妈妈的年龄是小明的6倍。
总之,教师要有意识、有目的地激发学生的学习兴趣,强化学生的思维能力。事实证明,通过恰当的引导、归纳和示范,可以使学生更好地理解知识、掌握技能、积累经验和感悟数学思想,进而使学生的思维能力得到高效发展。

