让数学探究在慢节奏中取得实效
——以苏教版教材五年级上册“三角形面积的计算”的教学为例
江苏淮安市实验小学新城校区(223001) 张 超
“三角形面积的计算”是苏教版教材五年级上册的内容,这部分内容的学习难点是理解“除以2”的意义。推导三角形面积计算公式需要很强的探究性,但学生的最近发展区严重制约着探究效率,使得很多探究活动流于形式,只见动静大,未见真效果。有时探究刚刚有“眉目”,便因时间有限而被紧急叫停。那么,如何才能让探究真正落到实处呢?现笔者以“三角形面积的计算”的教学为例进行论述。
一、分解步骤,扎牢探究基础
要想引领学生,首要的是找准学生的学习起点。通过前测发现,大多数学生习惯用直角三角形进行研究,通常先画出直角三角形,然后割补成长方形,再得出三角形的面积;少数学生选择用等腰三角形进行研究,沿着等腰三角形的底边中线裁剪,然后拼贴成长方形,从而间接求出三角形的面积。前测中,学生自动摒弃用任意三角形为模型的想法,道理很简单,直角三角形和等腰三角形更容易转化成长方形。
要实现真正的“数学探究”,应该创设足够的思考、尝试、推理、表达的空间,放手让学生探索如何推导三角形面积公式,让学生在具体实践中自主发现,体验到自主发现、自主解决问题的成就感。
依据前测,笔者决定放缓节奏,循序渐进,将探究过程延展成以下三个层次。
第一层次,探究直角三角形的面积求法。
学生自主探究出两种方法(见图1)。

图1
受直角三角形特殊性的影响以及自身经验的限制,在第一层次探究中,学生并未采用教材提供的“平行四边形拼合法”,基本上都是用图1的两种方法。方法一:将两个直角三角形拼合成一个长方形,求其面积的一半。方法二:将直角三角形沿某条直角边的中位线剪切,然后拼贴成一个长方形,拼贴后的长方形与原三角形面积相等,长方形与三角形同底,高则是其一半,于是得到三角形的面积=底×(高÷2)。
看着自己的探究成果,学生变得自信起来。
第二层次,探究等腰三角形的面积求法。
学生创造出四种方法(见图2)。
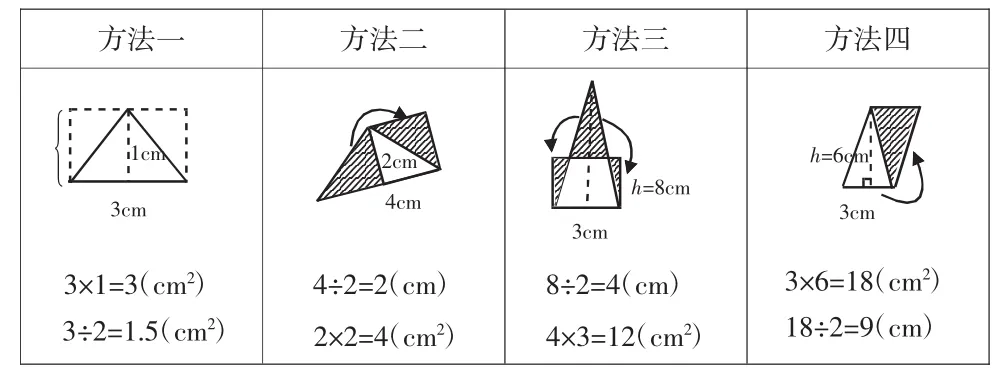
图2
以直角三角形的探究为基础,学生的思路彻底打开了,实现了“真探究”“真交流”。结合等腰三角形的特性,学生共创造出四种方法。整体思路是将原图形进行等面积的割补变换,“方法四”中的整体旋转复制法,虽然只有两位学生想到,但这已经是自主探究的飞跃。
第三层次,探究任意三角形的面积求法。
学生共创造出三种方法(见图3)。

图3
在展示汇报后,学生的思维轨迹暴露无遗,教师就可以顺着学生的思路进行引导,将最大的发挥空间留给学生,使学生经历多元化思维。探究任意三角形面积求法确实比探究直角三角形面积难度大,但是转化思想是一个渐进的过程,学生通过前两次特殊三角形的转化实践,对于任意三角形的转化也能慢慢熟练起来。
二、真实互动,渗透数学思想方法
“为什么用任意三角形为素材可以研究出三种方法?而用等腰三角形研究还多出一种方法?”学生在对比质疑中发现,对于前一个问题,以任意三角形为素材研究出的三种面积求法中,图3的“方法一”和“方法二”属于一类,都是将三角形扩充至2倍大小的四边形(“方法一”转化是为平行四边形,“方法二”是转化为长方形)后再还原成原来的面积大小,所以要除以2,是先求面积再除以2,而“方法三”则是将三角形转化成等面积的长方形,除以2的理由是三角形的高在中点处被切断,是先除以2后再求面积。对于后一个问题,等腰三角形比任意三角形多出一个“方法二”(如图2)——将等腰三角形沿着底边中线(高线)切割,分成两个全等的直角三角形,然后演变成直角三角形中的“方法一”。当学生用一幅幅生动的图画解析问题时,一部分学生深受启发,在惊叹“我怎么没想到”之余,感知到特殊三角形和一般三角形之间的异同,从而归纳出一般性结论,总结出三角形面积的计算公式:S=a×h÷2 或 S=a×(h÷2)。可见,推导三角形面积的计算公式时,要着眼长远,开放式地整体构架,以“自主探究”贯穿全程,在“三探三思”中,以探究为横线,以交流为总线,做理性探索。因为教师没有过多的干涉和要求,所以学生的转化方法百花齐放;因为教师没有过分的干预和掣肘,所以学生在探究活动中更深入,更收放自如,经历了“形变”到“质变”的思维过程,体验了公式的来历和原理,学会了从特殊到一般进行合情推理,能够用不完全归纳法得出三角形面积的计算公式,感悟到转化、归纳、抽象等数学思想。
三、放慢节奏,让探究变得真实
在教学三天后,再次安排测试。测试题如下。

正是由于体验维度扩展了,积淀变得更有层次感。测试结果显示,在公式中遗漏“除以2”的学生只有一个。这样,推导三角形面积的计算公式,从调查到测试,每个步骤都分散穿插于各教学课时的正常教程之中,潜移默化地完成了“三角形面积计算公式”的探究活动,耗时5天。
三个层次的探究,学生的体验是深刻、丰富、积极的,探究成果是丰硕的,上台交流是热情洋溢的,这种成功的体验是终身铭记的。其实,对于教材中的教学内容,机械重复练习实在没有必要,而探究活动却值得我们花费大量心血去设计规划。作为教师,应该为探究性强的内容规划一条较长的教学路线,拉长战线,与其一课时教完三角形面积内容,再花费大量时间去做巩固练习,一点点地试错、纠错慢慢积累,倒不如放慢步子,循序渐进,分步推进,让探究活动变得真实有效。

