借助动态直观图感悟假设法
——以“鸡兔同笼”问题的教学为例
安徽望江县第一小学(246200) 吴新结
人教版教材四年级下册安排了数学广角“鸡兔同笼”这一内容,展示了解决该问题的一些方法,体现了解决问题方法的多样性。其中,将假设法作为一种重要的数学思想方法进行了重点介绍,引导学生在学习中感悟假设法,同时培养学生的推理能力。
在实际教学这一内容时,我们存在许多困惑。一是“假设”这种想法,是教师给出的,而不是学生自然想到的,如何才能让学生自然地萌发这种思想呢?二是假设法伴随着较为复杂的分析推理过程,学生理解起来有一定的困难,如何帮助学生克服困难?三是如何抽象出假设法,使学生有所感悟并在新的情境中进行推广运用?
同时我们也了解到:在先前的学习中,学生从没有系统地接触过假设法,即在他们的知识结构中不存在“假设”这一图式,但他们在日常生活中不乏“假设”的经验,如“过家家”时角色的扮演、“假如”“当成”这些词汇的运用等。基于上述困惑和认识,我对“鸡兔同笼”这一内容中的假设法进行了新的教学尝试。
首先让学生通过画图尝试解决问题(如图1),师生交流解题思路。
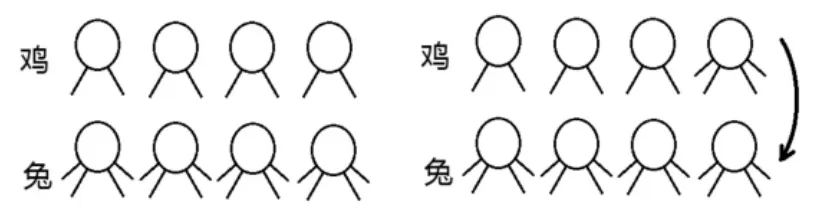
图1
生1:先把鸡和兔都看成是4只,画好后数一数,发现脚的只数少了,就再添上一些脚。
师:“先把鸡和兔都看成是4只”是一种很好的想法,数学上把它叫作假设。我们还可以怎样假设呢?
(学生分别假设鸡和兔不同的只数,就是没有假设“笼子里都是鸡”或“笼子里都是兔”这两种情况)
师(动画展示“玉兔拜月”):从数学的角度看,这时的兔子与鸡就没什么两样了,都是1个头、2只脚。如果笼子中的兔子都在拜月,这时候,笼子中的动物就可以全部看成什么?
生2:全部都是鸡。
生3:由既有兔又有鸡变成全部都是鸡,使问题变得简单了。
仅有这样的“启蒙”还是不够的。假设法要求:“在条件改变之后,根据题目的数量关系进行计算和推理,再根据所得数据与原数据的差异进行修正和还原,最后使原问题得到解决”。这样的一个基本思考过程,还是要让学生在动态的图示中去一步步体验和领悟。
接着,我引导学生根据上面的讨论,将笼子里的动物假设都是鸡,画出图2,并进行计算和推理,比较差异。
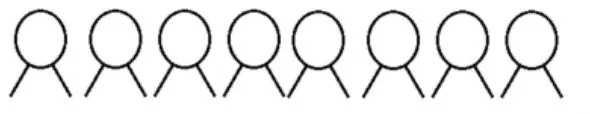
图2
生4:每只鸡有 2只脚,2×8=16(只脚)。实际有 26只脚,少了 26-16=10(只脚)。
师:这是什么原因呢?
生4:把兔子画成了鸡,脚数变少了。
(我顺势画出图3,再进行修正和还原)
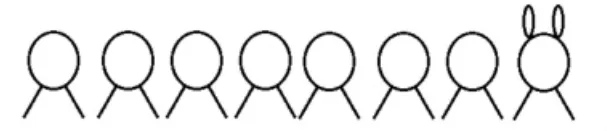
图3
师:把几只兔子画成了鸡?
生5:5 只。
师:你怎么知道是5只兔子呢?
(虽然学生已通过其他方法得知了鸡和兔的只数,但教师还是要追问推理的过程)
生5(展示推理过程):一共少画10只脚,每只兔子少画 2 只脚,10÷2=5(只)(兔),8-5=3(只)(鸡)。
(我出示图4,突出强调求出的是兔子的只数,这也是学生最容易混淆的地方)

图4
师:看了这些怪模怪样的兔子你有什么想法?
生6:把兔子的脚补上去。
(学生在作业纸上补画,教师用投影仪展示学生补画的图,如图5)

图5
师:现在符合条件了吗?算一算,检验一下。
生7:2×3=6(只),4×5=20(只),20+6=26(只),符合题意。
在上述教学过程中,我借助动态的直观图,逐步揭示用假设法解决问题的过程,学生在参与数学活动的过程中,对假设法有了一定的感受和体验。
数学思想方法的感悟不是一蹴而就的。就一节课来说,一种思想方法的学习也不能仅仅通过一两个例子去完成。要让学生将数学思想方法内化为自己的认知,并能自觉地在今后的学习中予以运用,教师就要注意一般方法的概括以及对学生迁移能力的培养。
在这节课的最后一个部分,我安排了以下几个教学内容。
1.如果假设全部是兔子,你是怎样思考的?请用画图法在小组内向同伴说一说你的想法。
2.“新星小学‘环保卫士’小分队12人参加植树活动,男同学每人栽了3棵树,女同学每人栽了2棵树,一共栽了32棵树。男女同学各有几人?”这个问题与“鸡兔同笼”问题有哪些相似的地方?能用画图法解决问题并说明你的想法吗?
3.不用画图,在脑中想象:鸡、兔共有6个头,16只脚。鸡、兔各几只?
这是一个递进的过程,从熟悉的“鸡兔同笼”问题,到情境不同但实质相同的植树问题,从具象到表象,所依托的仍然是图形。在这些感性材料的基础上,引导学生对假设法的一般程序进行初步总结。
课件再次展示以上学习中的直观图,逐步提炼假设法的一般程序:假设一种特殊的情况→根据数量关系计算相关数据→与原来的数据比较(找出不同)→分析这些不同的原因→计算得出正确的答案。
诚然,假设法并不止本文所述的这一种,这里仅以“鸡兔同笼”为例,假设的是一种极端的情况,而不是一般意义上的“对数学问题的一些数据做适当的改变”,是一种特例,其他情况有待于后续的学习。我们在这里只是播下一粒种子,期望今后开出更加美丽迷人的数学之花。
通过画图描述和分析问题,可以使复杂的数学问题变得简明、形象,有助于探索解决问题的思路,是培养学生思维能力的有力拐杖。可以说,通过画图解决问题,是学生数学素养的一个方面。本文所示的一些示意图,不仅使抽象的思想方法具体化、形象化,有助于学生感悟假设法,动态的生成过程,还契合了学生的思考路径,较好地发展了学生的数学思维。
从更一般的角度来看,“数学广角”教学内容所蕴含的数学思想方法大都有一定的思维难度,考虑到小学生的年龄和心理特点,借助一些直观的图形去体验感悟,是一条有效的路径。

