圆的面积计算公式创新教法

江苏淮阴师范学院附属小学（223001） 马乃骥

“圆的面积”是小学几何学习的重点，它是平面线条由直线向曲线过渡的知识转折，线条由直到曲，需要学生的思维有一些突破。理论上，曲边形应该采用微积分知识求面积，教材采用的实验法推导面积公式，间接渗透了极限思想。推导出圆的面积计算公式后，教材编排了两道公式应用类习题。课后，笔者进行了后测。后测试题如下：（1）如图1，若正方形的面积为36 cm2，则圆的面积是多少？（2）若正方形的面积为20 cm2，则圆的面积是多少？答题情况如下表。

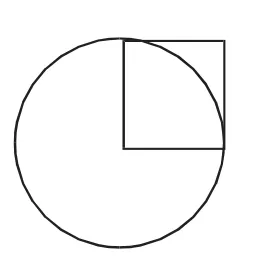
图1

题号 错误人数 总人数 出错率 典型错误第（1）题 10 90 11.11%（1）r=36÷4=9 cm，3.14×92=3.14×81=254.34 cm2。（2）r=6 cm，3.14×62=3.14×12=37.68 cm2。第（2）题 75 90 83.33% r=20÷4=5 cm，3.14×52=3.14×25=78.5 cm2。

一、分析诊断

1.对面积的意义理解不够深刻

在学习“圆的面积”之前，学生已经学过了简单的平面几何图形的面积，并能够说明白什么是面积。于是在教学“圆的面积”时笔者就没有复习面积的概念。后测结果显示，当正方形面积为20cm2时，学生求出正方形的边长为5 cm，其实是将面积与周长概念混淆了。

2.对公式的推理过程不清楚

后测数据显示，学生能顺利将平方数“36”分解成6cm×6cm，求出正方形的边长为6cm，观察图形可知，正方形边长等于圆形半径，然后根据圆的面积公式S=πr2，代入数据即可求出圆的面积。但是数据“36”变成“20”后，学生就做错了。他们总是先求出半径的具体数值，再代入圆的面积公式，完全没想到能将r2作为一个整体代入公式就可求解。

3.缺乏探究经历

教材是通过剪、切、拼、贴等将圆形分割成若干个近似的等腰三角形，然后交叉嵌入，形成一个近似的平行四边形（或者长方形），最终利用求四边形面积法推导出圆的面积计算公式。许多教师认为圆的面积计算公式的推导过程含有极限思想，超出小学生的认知范围，于是只要求学生记住面积公式。用单一的方法推导公式，学生无法经历“异中求同”的思维训练，缺乏对面积计算公式权威性和严谨性的认同。

二、解决对策

1.重视情境操作，感悟“面积意义”

研究表明，通过实践操作得到的面积概念信息是深刻、稳固而理性的。教学中，教师应设计一些操作环节，引导学生揣摩并体会圆的面积意义。

例如，在“圆的面积”一课开始，笔者设计这样的活动：

（1）描画，区分周长和面积

出示四个大小不一的圆形（如图2），让学生尝试描绘周长和面积。学生能用绕线法来感知周长，用剪纸法来感知面积，在比较中发现，周长是线条的长度，而面积是平面展开的大小。

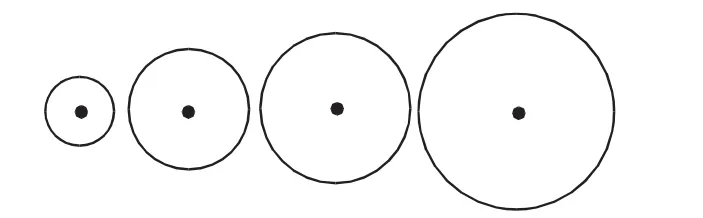
图2

（2）比较、感悟面积与什么有关

面对四个不同大小的圆形，学生会在观察和比较中思考：圆的面积大小跟圆的什么有关？在初步交流中发现，影响圆的面积大小的因素主要是直径和半径。在教学中，充分运用比较的方法，有助于突出引起面积大小变化的主因。

2.借助几何直观，聚焦“公式本质”

在探究“圆的面积”时，可利用几何直观充分揭示其与正方形面积的关系，并通过计算理解公式本质。

（1）感知圆与正方形面积的大小关系

呈示三个不同的正方形和一个圆（如图3），引导学生观察分析，判断它们的面积大小关系。

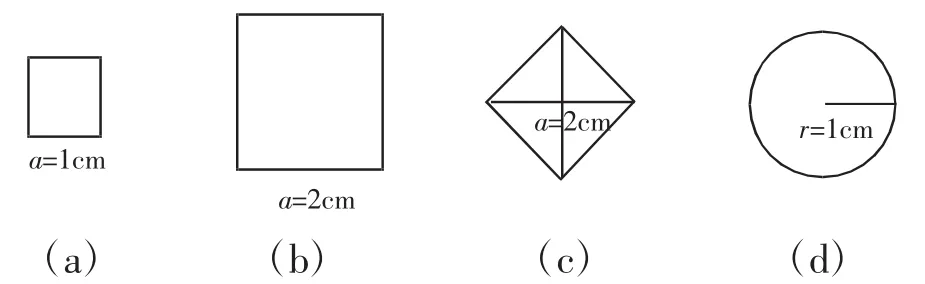
图3

先让学生比较三个正方形的面积大小，通过计算，学生发现图（b）正方形面积是图（a）正方形面积的4倍，图（c）正方形面积是图（a）正方形面积的2倍。学生会感到好奇，“图（d）圆的面积是图（a）正方形面积的多少倍呢？”从而发现正方形面积和圆的面积有个共同部分就是1cm2。

（2）感知圆的面积与正方形面积的大小关系

先画出一个正方形，再以正方形的顶点为圆心、边长为半径画圆，估测：圆的面积与正方形面积的倍数关系。（如图4）

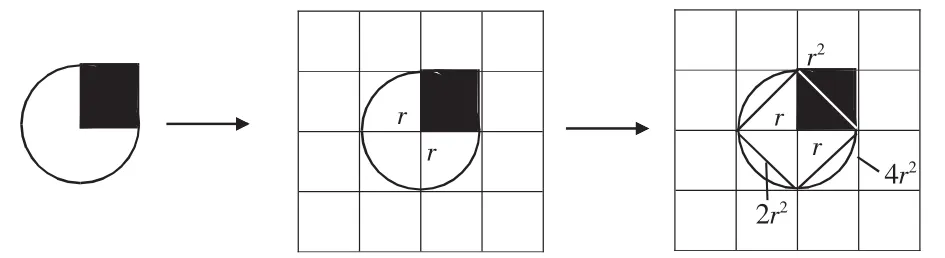
图4

从原始的“数方格”起步，作出辅助线、圆的内接正方形和外切正方形，进行转换和间接对比，得出圆的面积约为正方形面积的2至4倍，让学生明确：圆的面积与r2成正比，比值为圆周率。

三、探索验证

1.于多种形式的探索中体验转化思想

可直接要求学生用割补法将圆形转化为已经学过的几何图形，以小组为单位合作探究圆的面积计算公式。由于圆的大小以及分割的份数不一样，学生得到了多种多样的方案。学生通过观察实践，发现可以将圆形转化为近似的长方形，分得越精细，越接近长方形，再通过转化前后的对比，发现了变化量和恒等量，从而推导出圆的面积计算公式。

2.以不同的推演方案验证公式的可信度

教材只提供了“转化为长方形”这一种转化模式。为了追求多样性，笔者引导学生求异求变：“以平分成16份为例，除了长方形，还可以拼接成什么图形？能利用新图形推导圆的面积计算公式吗？”

学生通过将圆转化成三角形、梯形（如图5），从不同角度推导出了圆的面积计算公式，经历不同的推导过程后，转化思想得以培养。

图5

站得高才能看得远。一切尝试得出的结果只有经过多番证明，才显得真实可靠。正是因为有了前面正方形的引领，后面的多样性重组法才有了坚固的理论根基。

综上，圆的面积计算公式推导是几何教学中的重要内容。只有创新教学方法，让学生通过观察、拼接等探究方法，将面积计算公式盘活，并能融会贯通、运用自如，才能有效解决面积计算问题。