基于圆锥曲线一种切线画法的试题命制

福建省泉州第五中学 (362000) 李萍萍 杨苍洲

1.圆锥曲线切线的作法

1.1 过椭圆上点S的切线的作法

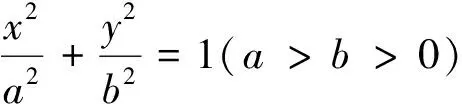
①任作一条直线m垂直于椭圆的长轴A1A2；

②作直线A1S、A2S分别交直线m于I、J两点；

③作线段IJ的中点T，则直线ST即为所求的切线l.

图1

设IJ的中点T(x1,y1)，则x1=t，y1=

图2

1.2 过双曲线上点S的切线的作法

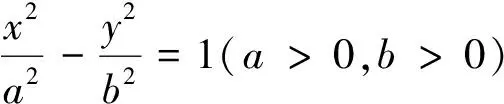
①任作一条直线m垂直于双曲线的实轴A1A2；

②作直线A1S、A2S分别交直线m于I、J两点；

③作线段IJ的中点T，则直线ST即为所求的切线l.

证明同上.

1.3 过抛物线上点S的切线的作法

设抛物线y2=2px(p>0)的顶点为O，S为抛物线上一点，过点S作抛物线的切线l，作法如下：

①任作一条直线m垂直于抛物线的对称轴；

②作直线OS交直线m于I点，作平行于对称轴的直线SJ交直线m于J点；

③作线段IJ的中点T，则直线ST即为所求的切线l.

证明同上.

2 基于圆锥曲线切线作法的试题命制

题1 已知抛物线x2=2py(p>0)，焦点F到准线l的距离等于2.

图3

(Ⅰ)求抛物线E的方程；

(Ⅱ)若直线AB过抛物线的焦点F交抛物线于A,B两点，C,D为l上的两点，AC⊥l,BD⊥l,E为线段CD的中点，证明：AE,BE分别与抛物线C相切于点A,B.

解析：(Ⅰ)∵p=2，∴抛物线x2=4y.

同理可证：直线BE与抛物线相切.

图4

(Ⅰ)求椭圆E的方程；

(Ⅱ)给出命题：“已知P是椭圆E上异于A1,A2的一点，直线A1P,A2P分别交直线l:x=t(t为常数)于不同两点M,N,，点Q在直线l上.若直线PQ与椭圆E有且只有一个公共点P，则Q为线段MN的中点”，写出此命题的逆命题，判断你所写出的命题的真假，并加以证明;

(Ⅲ)试研究(Ⅱ)的结论，根据你的研究心得，在图5中作出与该双曲线有且只有一个公共点S的直线m，并写出作图步骤.

(注意：所作的直线不能与双曲线的渐近线平行.)

图5

(Ⅱ)逆命题：“已知P是椭圆E上一点，直线A1P、A2P分别交直线l:x=t(t为常数)于M、N两点，若Q为线段MN的中点，则直线PQ与椭圆E有且只有一个公共点P”为真命题.

证明如下：

图6

(Ⅲ)如图6，①任作一条直线n垂直于实轴；②作直线A1S、A2S分别交直线n于I、J两点；③作线段IJ的中点V，则直线SV即为所求的直线m.