一种联合小波阈值和维纳滤波的探地雷达信号去噪方法

张梦殊，那振宇，梁道轩，熊木地*，刘鑫

（1.大连海事大学信息科学技术学院，辽宁 大连 116026；2.大连理工大学信息与通信工程学院，辽宁 大连 116024）

1 引言

探地雷达是一种具有探测速度快、实时成像特点的无损探测仪器，被广泛应用在考古学[1]、地下能源勘探[2-3]、道路桥梁质量检测[4]、公共安全与军事探测[5]等领域。在实际探测过程中，为了能够使探地雷达获得更全面的目标反射回波信号特征，一般选用宽频带进行记录，这就使得在记录有效回波的同时，不可避免地将频带内的噪声也记录下来。

为了能够从含噪的雷达回波信号中准确提取出目标信号，学者们提出了各种去噪方法。许军才等[6]提出了基于集合经验模分解（EEMD, Ensemble Empirical Mode Decomposition）的探地雷达信号时域分析方法。该方法克服了经验模分解（EMD, Empirical Mode Decomposition）方法的模态混频现象，在去除信号中的白噪声时效果显著。Xun等[7]利用信号分解方式实现了主成分分析法-奇异值分解（PCA-SVD, Principal Component Analysis-Singular Value Decomposition）混合去噪方法，得到了较好的去噪效果。陈瑞鼎等[8]利用卡尔曼滤波对雷达回波信号进行杂波抑制，将原始信号分解为目标信号、背景信号和噪声信号，最后对目标信号沿空间方向进行了快速傅里叶变换，获得了较好的目标信号特征。王超等[9]提出了基于希尔伯特-黄（HHT, Hilbert-Huang）变换去除雷达回波信号噪声的方法。该方法摆脱了传统傅里叶变换的约束，但是在利用HHT变换时忽略了相邻两道雷达回波的数据影响及周围噪声的连续性。Gan等[10]提出了一种基于二维经验模态分解（BEMD, Bi-dimensional Empirical Mode Decomposition）和小波阈值的去噪方法，提高了雷达图像的解译准确度。石显新等[11]提出了一种方法，利用二维物理小波函数模拟与目标信号相匹配的小波函数，并结合小波阈值去噪，获得了较好的去噪效果。杨建功等[12]指出在对探地雷达信号进行去噪处理时，小波分析的去噪效果优于常规的去噪方法，可以根据信号与噪声的小波系数性质不同，采用相应规则对含噪信号进行小波阈值去噪，能够较好地抑制噪声，提高信噪比。

通过以上分析可以看出，探地雷达信号的去噪可以在时域、频域或时频域联合实现。无论哪种实现方式，都是利用有效信号和噪声在频域内分布不相同这一特点。传统的去噪方法往往将包含噪声的高频部分全部去除，但这使得去噪的同时也去除了高频部分含有的有效信号。而基于小波变换的阈值去噪方法能够解决这一问题，但是传统的小波阈值去噪方法没有对低频部分进行去噪，这就导致了去噪不完全。因此，本文提出了一种联合小波阈值和维纳滤波的探地雷达信号去噪方法。该方法是在小波阈值去噪的基础上，使用维纳滤波对低频部分进行处理，实现更完全的去噪。仿真结果表明，该方法相比传统的小波阈值去噪方法能够获得更好的去噪效果，特别是在低信噪比时效果更为明显。

2 小波阈值去噪

探地雷达接收天线接收到的原始雷达回波信号由目标反射波、杂波和噪声组成。为便于分析，不考虑杂波的影响，则雷达回波观测信号可以表示为：

对式(1)两边做小波变换得到：

式中，wj,k表示含噪的雷达回波信号w(n)的小波系数，sj,k和uj,k分别表示目标回波信号s(n)和噪声信号u(n)的小波系数。

由于目标信号对应的小波系数的幅值都要比噪声信号对应的小波系数的幅值大，并且主要分布在低频小波系数中。因此，可以设置一个合适的阈值λ，令小波系数与λ比较。当小波系数小于λ时，认为该系数是噪声对应的小波系数，将其设为0。否则认为该系数是有效信号对应的小波系数，将其保留或进行收缩，从而得到各尺度下阈值处理后的小波系数ŵj,k，然后根据ŵj,k进行重构得到目标信号的逼近ŝ(n)。

一般地，含噪雷达回波信号的小波阈值去噪过程如图1所示。

从图1中可知，雷达回波信号小波阈值去噪可分为如下三个步骤：

（1）小波变换。根据选取的小波基与分解层数m，对含噪的雷达回波数据进行m层小波分解。图2是一个m=3的分解示意图，其中w(n)表示含噪的雷达回波信号，Ci(i=1, 2, 3)表示各层分解出的低频小波系数，Di(i=1, 2, 3)表示各层分解出的高频小波系数。

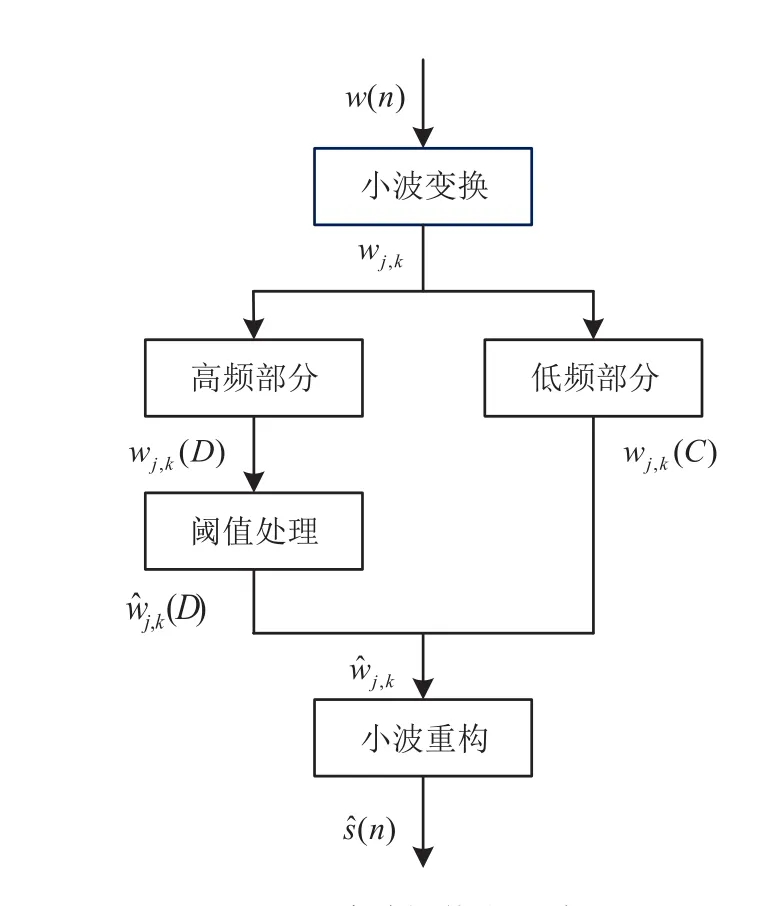
图1 小波阈值去噪过程

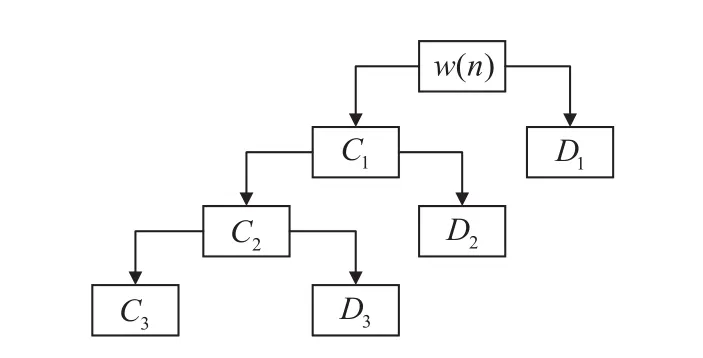
图2 小波三层分解示意图

（2）阈值处理。为保持雷达回波信号的整体形状不变，对分解出的低频小波系数不做处理，对每层的高频小波系数wj,k(D)进行阈值处理得到ŵj,k(D)。

3 小波域维纳滤波

维纳滤波仅限于处理平稳随机信号[13]，而探地雷达回波信号往往不具有该特性。但是，小波变换能够对信号起到白化作用，可较大程度地降低信号的非平稳随机特性[14]。所以，可以将雷达回波信号经过小波变换后再进行维纳滤波处理。

令σ2j,k和σ2分别表示式(2)中目标回波信号小波系数sj,k和噪声信号小波系数uj,k的方差，则维纳滤波器可以表示为：

假定σ2已知，而可用含噪信号小波系数的方差估计得到。由于有效信号和噪声信号互不相关，因此：

又由于σ2j,k≥0，所以：

将式(6)代入式(3)中，则维纳滤波器可以表示为：

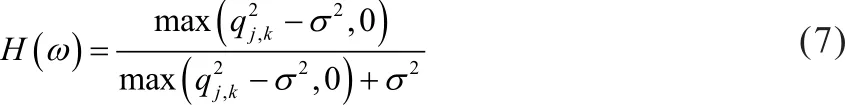
将待去噪数据与式(7)相乘即可得到无噪数据的最优线性估计。

4 小波阈值和维纳滤波联合去噪

由前面小节分析可以看出，含噪的信号在经过小波变换后得到的低频小波系数中也是含有噪声的。而在小波阈值去噪过程中的第二步，由于仅对探地雷达回波信号的高频小波系数进行了小波阈值去噪，因此会导致小波阈值去噪不完全。本文将维纳滤波应用于小波变换后的低频小波系数的去噪处理，将小波阈值去噪和维纳滤波结合，提出联合小波阈值和维纳滤波的探地雷达信号去噪方法。该方法的去噪实现过程如图3所示。

联合去噪方法的实现同样分为三步。其中，第一步和第三步与小波阈值去噪方法相同，第二步是在小波阈值去噪的基础上加入了维纳滤波。

为了不出现二次去噪的情况，图3中只对小波分解得到的最后一层的低频小波系数进行维纳滤波处理。

由式(5)和式(7)可求得低频部分各小波系数的估计，即：

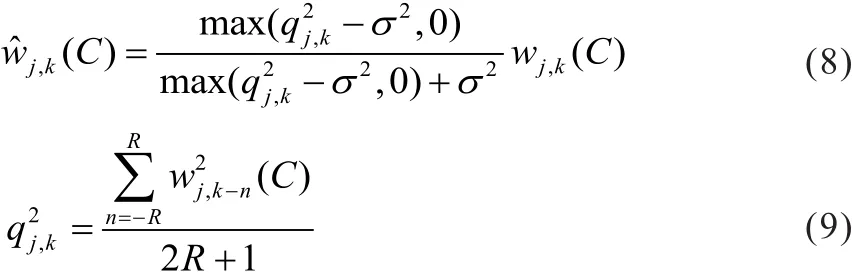
5 实验结果分析

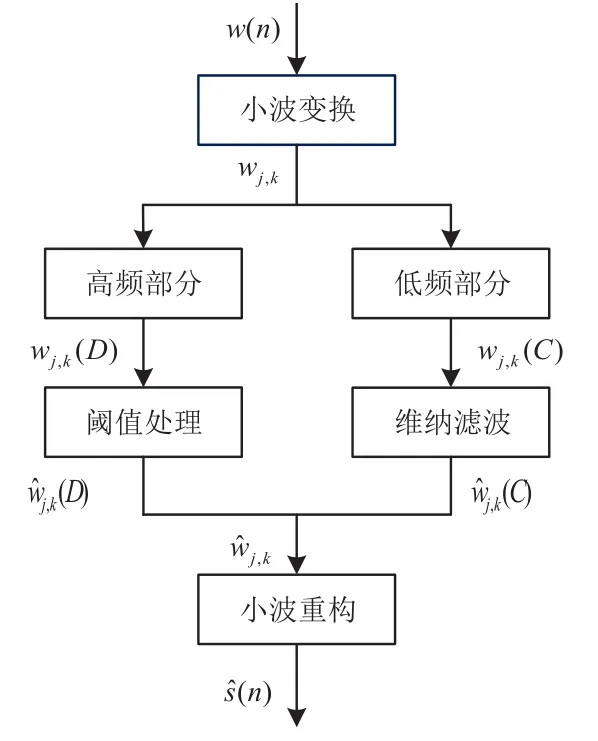
图3 联合去噪过程

为了验证本文提出的联合小波阈值和维纳滤波去噪方法的有效性，下面使用小波阈值去噪中不同的阈值函数和维纳滤波进行联合去噪，并与传统的仅使用小波阈值进行去噪的方法进行对比。图4为去噪仿真时用的单道探地雷达回波原始信号：

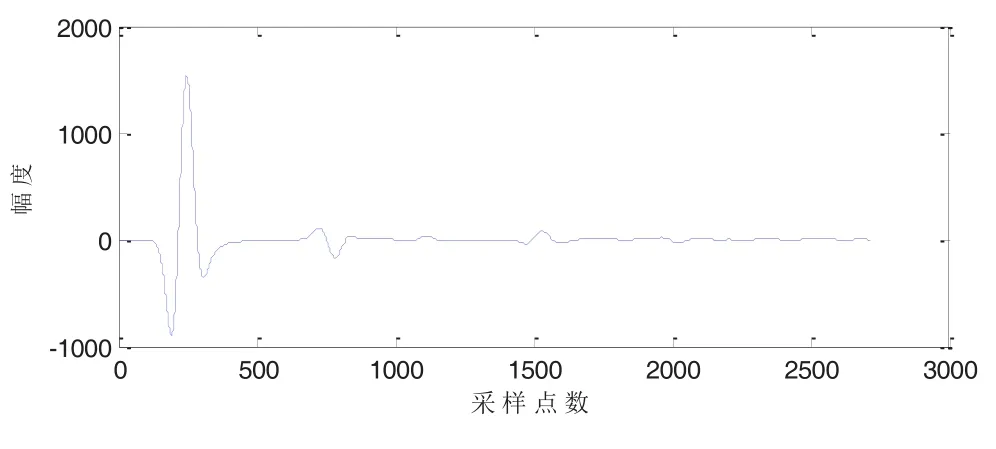
图4 探地雷达单道回波

去噪效果的评价指标除选用信噪比（SNR,Signal to Noise Ratio）和均方根误差（RMSE, Root Mean Square Error）外，还引入了相关系数（CC,Correlation Coefficient）评价方法[15]。其定义分别为：

式中，x1(i)表示不含噪的原始信号，x2(i)表示去噪后的信号，N表示信号长度。得到的SNR和CC的数值越大、RMSE数值越小表示去噪效果越好。

图5是传统小波阈值去噪方法中采用硬阈值函数时，有联合维纳滤波和无联合维纳滤波两种情况的去噪指标对比。图例中的“硬无”表示仅使用了硬阈值函数进行小波阈值去噪，“硬有”表示在使用硬阈值函数进行小波阈值去噪的同时联合维纳滤波去噪。图6是传统小波阈值去噪方法中采用软阈值函数时，有联合维纳滤波和无联合维纳滤波两种情况的去噪指标对比。其图例中的“软无”和“软有”含义与图5类似。从图5和图6均可以看出，与传统的小波阈值函数去噪方法相比，本文提出的联合小波阈值和维纳滤波去噪之后得到的SNR、RMSE和CC均有所改善，并且在低SNR下的去噪指标改善较为明显。这是因为含噪信号在经过小波变换之后，得到的低频小波系数中所含噪声会随着信噪比的降低而增加，对低信噪比下的低频小波系数进行维纳滤波处理能够除去更多的噪声，从而使得去噪效果较好。

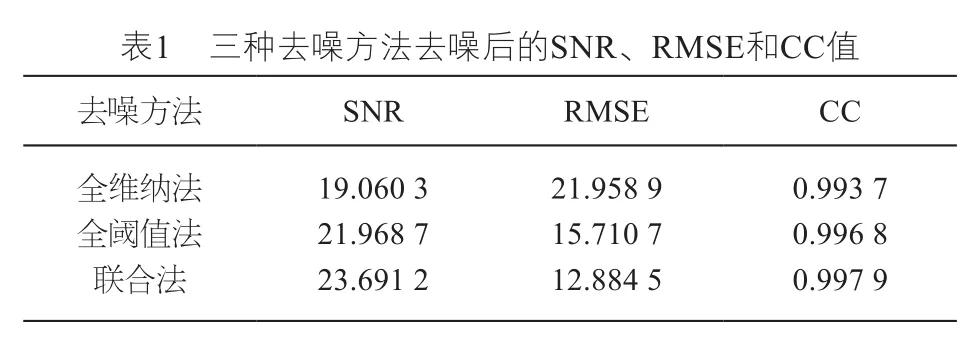
图7为硬阈值函数和维纳滤波联合去噪（简称联合法）、高低频小波系数均使用维纳滤波去噪（简称全维纳法）、高低频小波系数均使用硬阈值函数去噪（简称全阈值法）的去噪指标对比。从图中可以看出，联合法比全阈值法和全维纳法得到的去噪效果更好，得到的SNR和CC值最大，RMSE值最小，进一步证明了本文提出的联合去噪方法的有效性。

对图4中的单道回波进行加噪，得到信噪比为10 dB的含噪信号，然后用图7中的三种去噪方法对该道含噪信号进行去噪处理，图8为去噪后的波形图。在表1中给出了对应的SNR、RMSE和CC值。

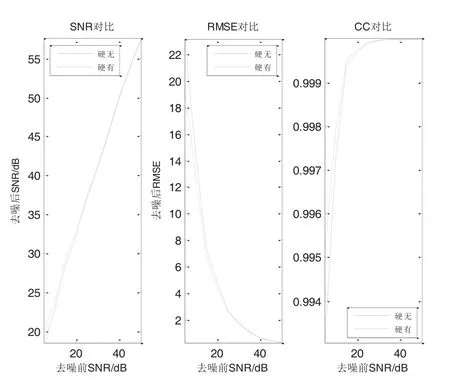
图5 硬阈值函数有无联合维纳滤波的去噪指标对比

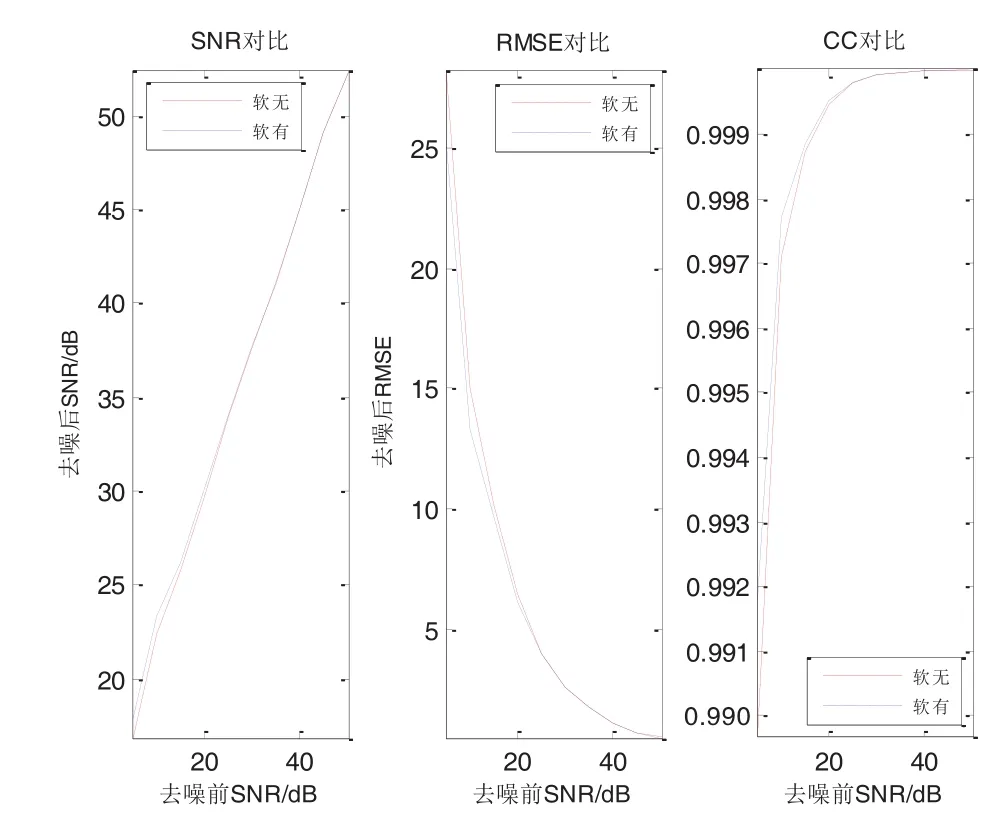
图6 软阈值函数有无联合维纳滤波的去噪指标对比

?

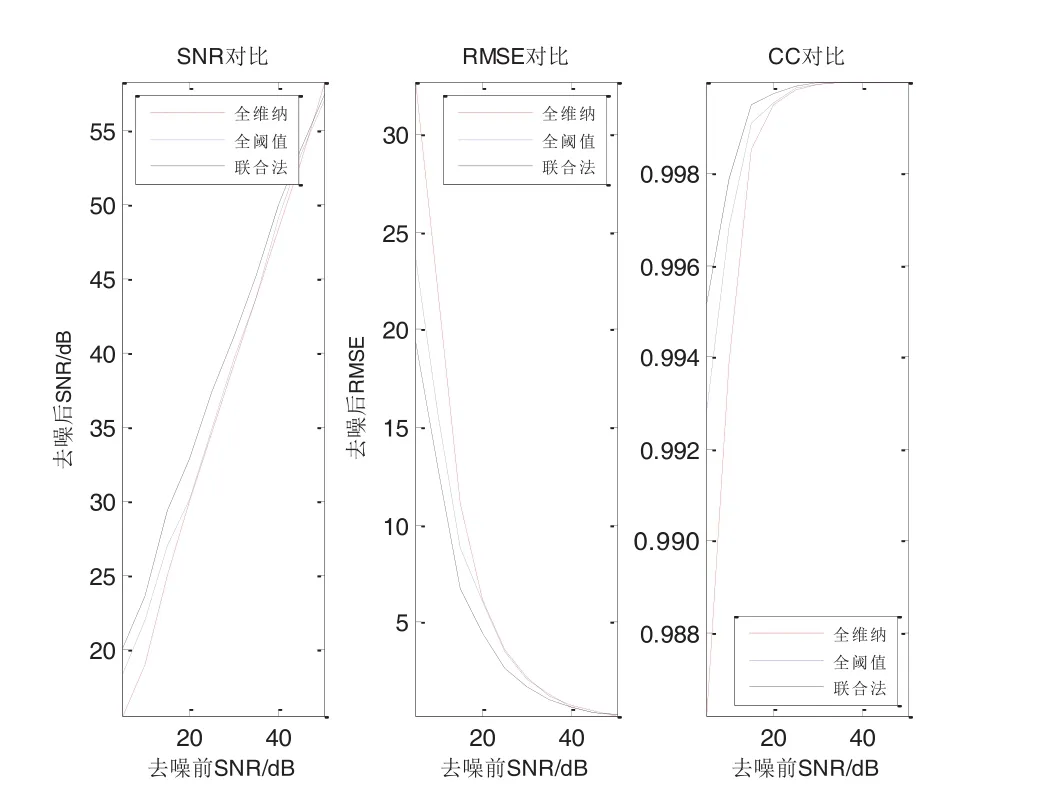
图7 三种去噪方法去噪指标对比

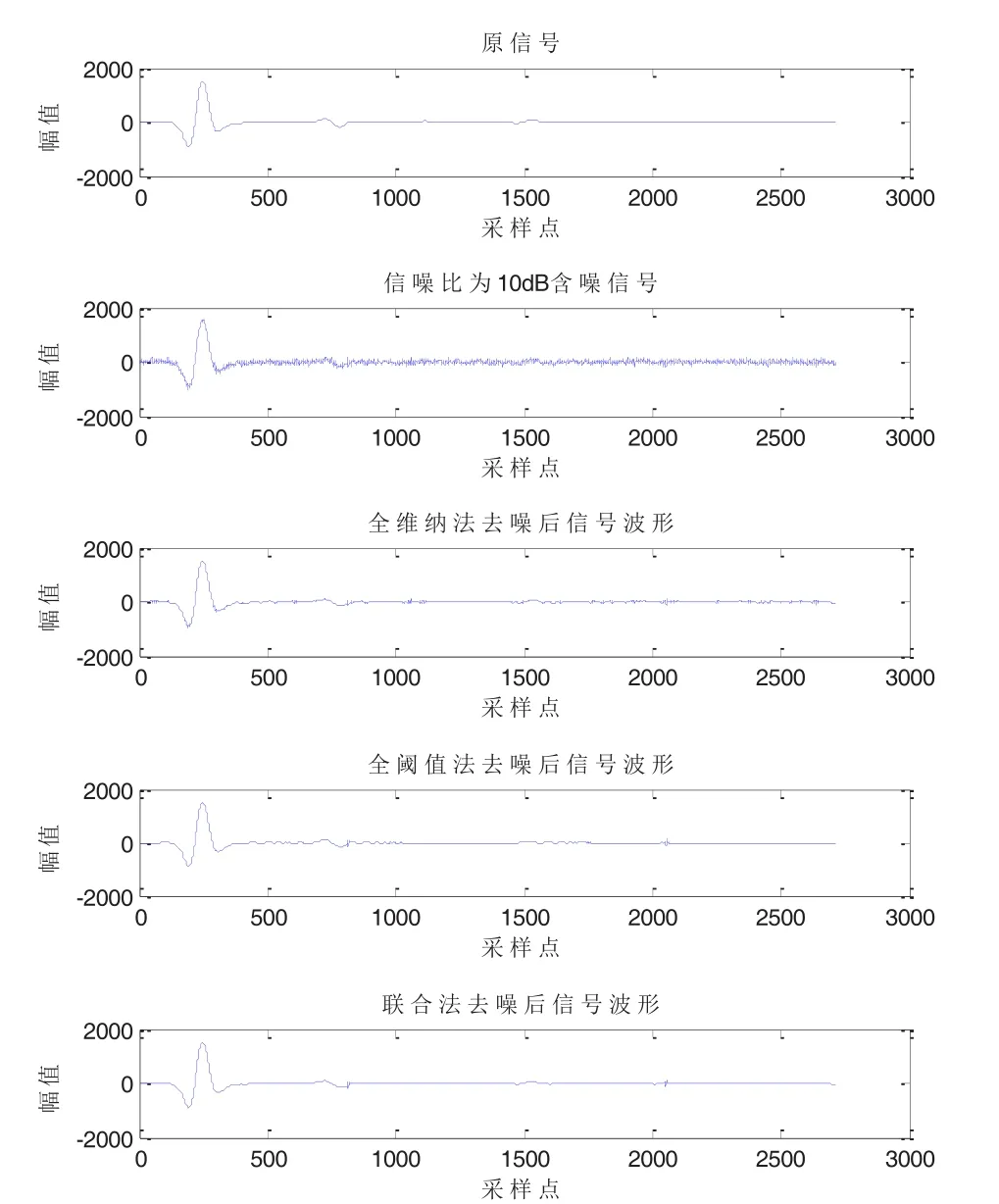
图8 三种去噪方法去噪后的波形图

6 结论

探地雷达信号的去噪是正确接收目标回波信号的前提。本文针对利用传统小波阈值方法对探地雷达信号去噪时，无法对回波信号的低频小波系数进行去噪的情况，提出了一种联合小波阈值和维纳滤波去噪方法。该方法是在小波阈值去噪的基础上，对分解出的低频小波系数进行维纳滤波处理。仿真结果表明，联合去噪方法相比传统的小波阈值去噪方法得到的波形更接近原始信号，并且得到的去噪指标值SNR和CC最大，RMSE最小，由此可说明本文提出的联合去噪方法可以获到更好的去噪效果。