3-P(4S)并联平台振动特性分析与实验验证

赵星宇 赵铁石 徐雪寒 赵延治 李忠杰

(1.燕山大学河北省并联机器人与机电系统实验室, 秦皇岛 066004；2.燕山大学先进锻压成形技术与科学教育部重点实验室, 秦皇岛 066004)

0 引言

为了实现更好地振动模拟及测试，将并联平台应用到振动领域是国内外的研究热点[1-7]。美国的MTS公司生产了多种类型的振动台，其中354.2型六维振动台可应用于大型设备的地震模拟，323.2型六维振动测试台可应用于汽车零部件的振动测试[8-9]。美国TEAM公司生产的电液伺服驱动六自由度振动台，可用于汽车组件的测试[10-11]。德国Instron公司生产的六自由度振动台，采用电液驱动形式，可应用于整车的振动模拟以及疲劳测试[12-13]。日本IMV公司生产的大型六自由度振动台可应用于地震模拟[14]。加拿大QUANSER公司生产的六自由度振动台，主要应用于小型设备的低频率振动测试[15]。中国水利水电科学研究院研制了一种三维平动的振动模拟台，可应用于地震模拟以及大型设备的动力试验[16]。中国科学院长春光学机械研究所基于传统的Stewart构型设计了一款多维振动模拟平台，可用来模拟空间环境中的多维扰动[17]。上海交通大学自主研发的多维电动振动台，可用于多维振动模拟[18]。

本文在文献[19]的研究基础上，对3-P(4S)平台的振动特性进行深入分析，首先建立机构的简化振动模型，并应用仿真软件进行验证，然后对机构的固有频率随运动位置变化特性和灵敏度特性进行分析，并通过实验进行验证。

1 3-P(4S)机构振动模型

1.1 振动方程的简化

图1为3-P(4S)并联平台三维造型和结构简图[19]。该机构由上平台、基座以及3个P(4S)分支组成，其中驱动部件为包含磁力弹簧的直线电机。机构简图中坐标系的建立以及结构参数的意义在文献[19]中已阐明，该机构有沿着xp、yp、zp的3个平动自由度，且其动力学方程可表示为[19]

(1)

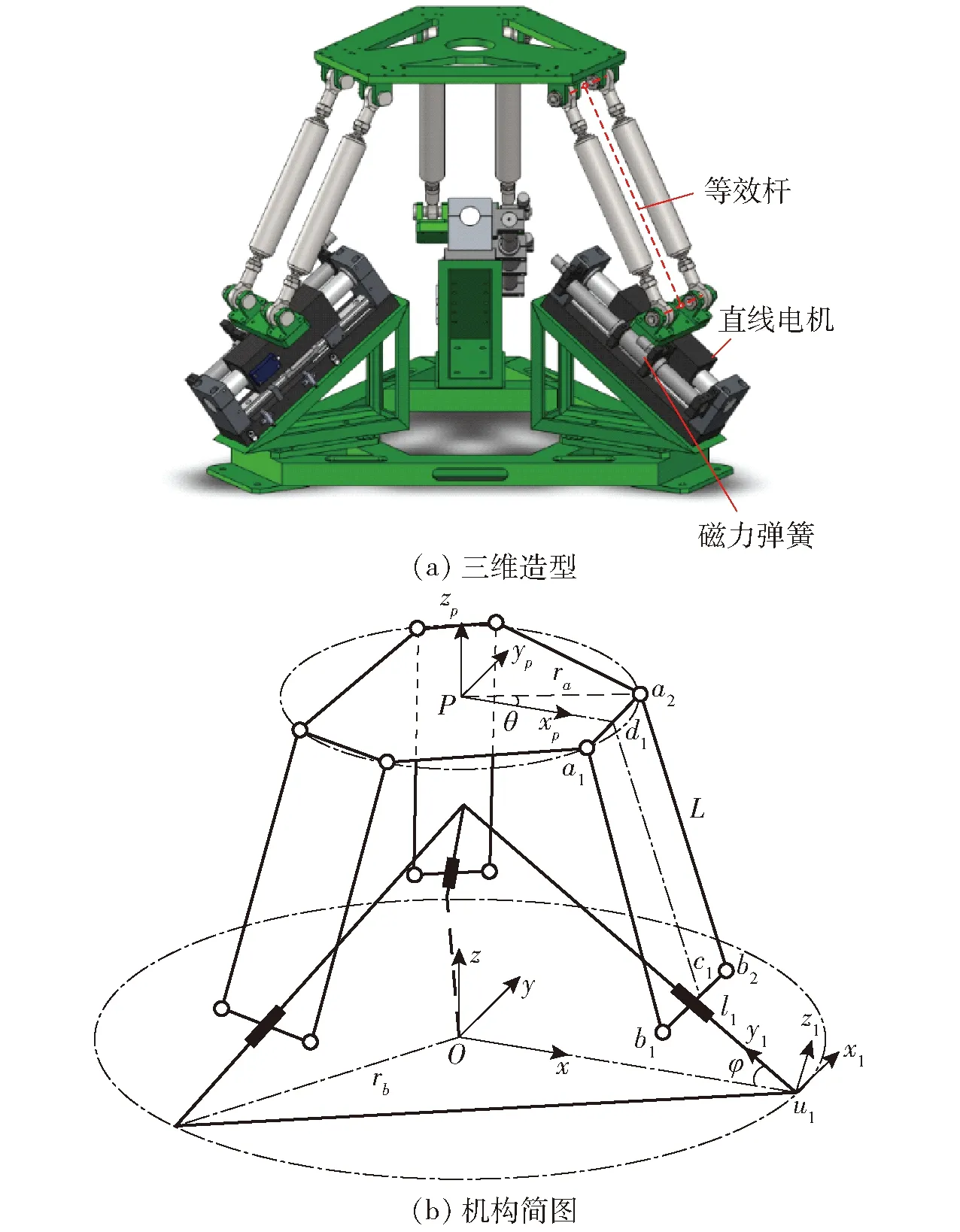
图1 3-P(4S)并联机构Fig.1 3-P(4S) parallel mechanism

式(1)出自文献[19]中式(23)，为了避免符号重复，故本文中用E和F代替文献[19]中式(23)的M和N。在振动分析过程中，只考虑电机的伺服刚度，假设其他构件为刚性件，则有

τA=Kq

(2)

其中K=diag(k1，k2，k3)

式中K——直线电机广义刚度矩阵

ki——直线电机的伺服动刚度，i=1,2,3

其测定值为ki=2.19×106N/m。

由于τG为常数项，而求解机构的固有频率的实质在于求解动力学方程拉普拉斯变换后的微分方程，常数项对其无影响，可忽略，则式(1)可表达为[19]

(3)

其中

则式(3)可化简为

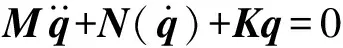
(4)

其中M=EJ-1

式中M——广义质量矩阵

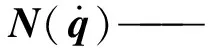
(5)

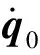
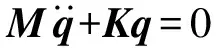
(6)

假设外界激励为F，则振动方程可表示为

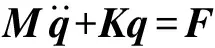
(7)

1.2 固有频率及振型

对式(7)做拉普拉斯变换，可得

(s2M+K)q(s)=F(s)

(8)

式中q(s)、F(s)——振动响应和外界激励的Laplace变换结果

令Z(s)=(s2M+K)，根据线性系统有s=jω，则Z(ω)=(K-ω2M)。则机构的振动特征方程为

Δ(ω2)=det(K-ω2M)=0

(9)

在无阻尼自由振动下，振动响应可列为

q(ω)=uqr

(10)

式中u——振型向量

qr——对应的坐标矩阵

(11)

式中un——机构第n阶振型向量

ωn——机构第n阶固有频率

(12)

式中urr——机构的正则主振型

通过式(12)可得到机构的正则固有振型u=[u11u22u33]T。

1.3 数值算例

该机构的结构参数如表1所示，将结构参数代入1.2节，可求得机构在初始位置下的固有频率及正则固有振型向量，如表2所示。

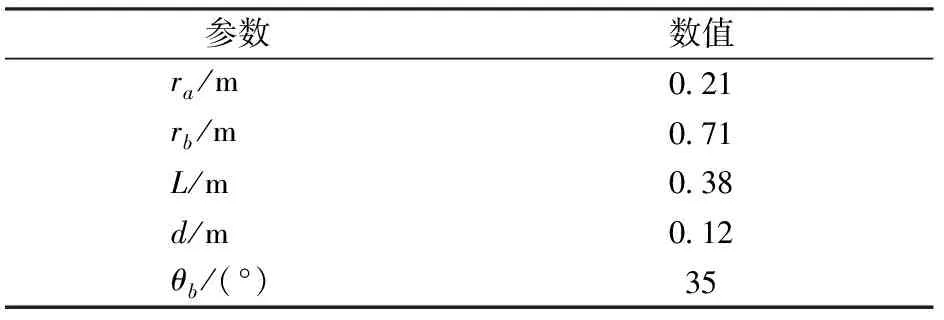
表1 结构参数Tab.1 Mechanism parameters

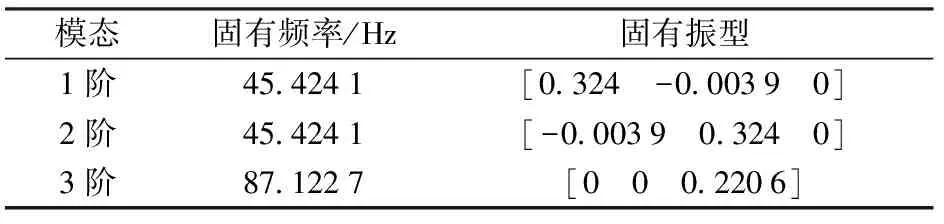
表2 固有频率及固有振型Tab.2 Natural frequencies and natural modes

由表2可知，机构的1阶和2阶固有频率的值均为45.424 1 Hz，并根据其固有振型，可将1阶主振动视作为沿xp方向的平动，2阶主振动作为沿yp向的平动。机构的3阶固有频率为87.122 7 Hz，其主振动为沿zp方向的平动。

为验证振动台的理论模型，应用ADAMS进行振动仿真分析。由于该直线电动机实际为欠阻尼，其阻尼数值对振动台固有频率的影响可忽略，并和理论推导保持一致，所以在驱动位置添加弹簧时只设定具体刚度，阻尼设为零，并假设振动台的各构件是刚性的。首先定义机构激励的输入通道，在机构上平台中心点P处，分别建立3个沿移动坐标轴方向上的正弦激振力，力的大小均为500 N，相角均设为零；其次，定义输出响应通道，同样输出响应的拾振点选在上平台的中心点P处，选择沿3个移动坐标轴xp、yp、zp的方向为拾振方向，选择测量类型为输出位移，通过模态仿真，可以得到机构的各阶模态，如图2所示。

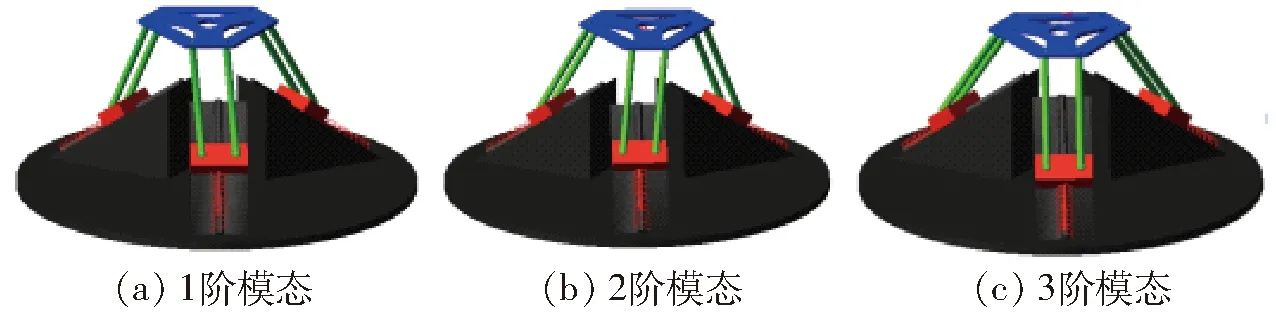
图2 3-P(4S)平台各阶模态Fig.2 Sketches of modes of 3-P(4S) mechanism

通过给定仿真步长以及测量频率的范围，可分别测得的机构沿xp、yp、zp方向的输出响应的幅频特性曲线，并将其数据点导入Matlab中进行显示，如图3所示。

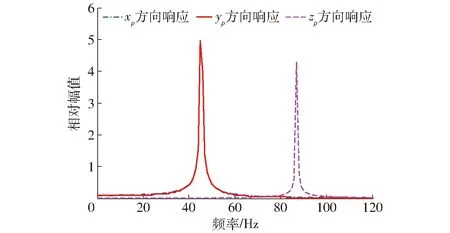
图3 振动幅频曲线Fig.3 Amplitude frequency curves of vibration

如表3所示，通过将理论计算以及ADAMS仿真所得到的机构固有频率的结果相对比可知，两者结果很接近，两者误差均在0.5%以内，说明应用振动方程得到的计算结果足够精确，可以作为进一步计算的依据。

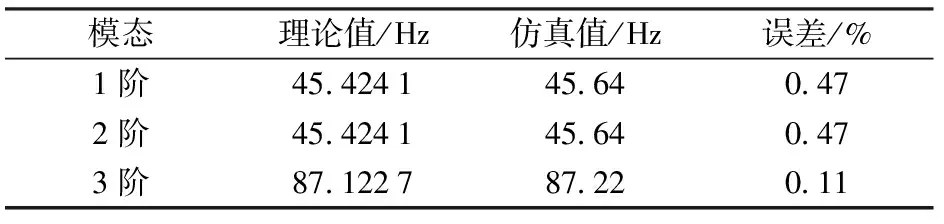
表3 固有频率对比Tab.3 Contrast of natural frequencies

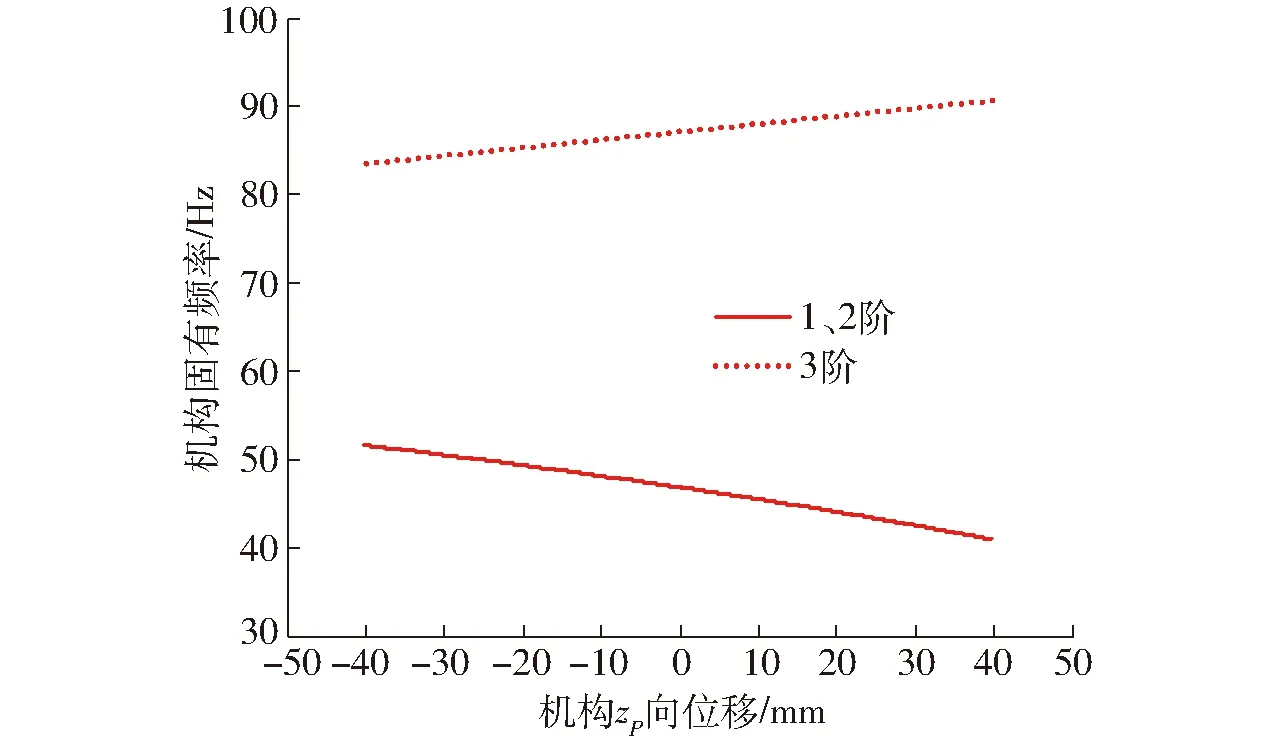
图4 zp向运动时固有频率变化Fig.4 Natural frequency variation of motion zp

2 振动特性分析

2.1 机构固有频率随位置变化分析

假设该平台在中心线上沿zp向运动，根据式(9)可得，机构固有频率变化如图4所示，其1、2阶固有频率沿zp向位移的增加而递减，3阶固有频率沿zp向位移的增加而递增。

假设机构在初始高度下，沿xp和yp方向运动，根据式(9)，固有频率的变化如图5所示，其1阶固有频率在初始位置有最大值，向运动空间的四周扩散递减，而2、3阶固有频率在初始位置最小，向运动空间的四周扩散递增。

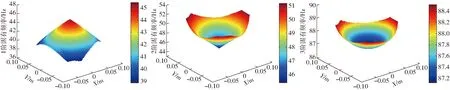
图5 机构的固有频率变化Fig.5 Changing charts of natural frequency of mechanism

2.2 机构固有频率灵敏度分析

(13)

设x代表各结构参数，求导可得到

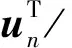
(14)

将式(14)展开并化简，可得

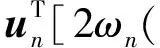
(15)

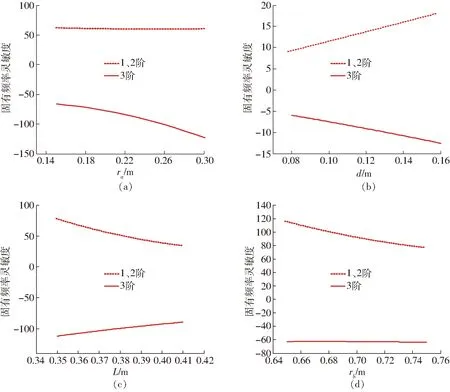
图6 固有频率对各结构参数的灵敏度Fig.6 Sensitivity of natural frequency to various structural parameters

将机构固有频率随结构参数变化趋势称为灵敏度特性，其表达式为

(16)

式(16)表示了机构的结构参数对振动特性的影响程度。设机构处于初始位置,可得机构的固有频率对各结构参数的灵敏度如图6所示。

由图6a可知，随着ra的增大，机构的1、2阶固有频率的灵敏度为负值但其绝对值逐渐增加，而3阶固有频率灵敏度近似为恒定的正值。这说明随着ra的增大，该机构的1、2阶固有频率逐渐减小，并且其减小的幅度越来越大，而3阶固有频率呈递增趋势，并且其与ra近似呈线性关系。由图6b、6c可知，机构的1、2阶固有频率对d和L的灵敏度均为正，3阶固有频率对d和L的灵敏度均为负，但其变化趋势相反。这说明随着d和L的增大，机构的1、2阶固有频率不断增加，但增加幅度不同，而3阶固有频率变化趋势相反，两者的灵敏度都逐渐减小，且减小幅度也不同。由图6d可得，随着rb的不断增大，1、2阶固有频率灵敏度为正且递减，而3阶固有频率灵敏度为负且保持不变。这说明随着rb的增加，1、2阶固有频率逐渐增加，3阶固有频率单调减小，并且与rb呈线性关系。

对于振动台而言，1阶固有频率对其振动特性以及振动台的工作状况影响最大。因此，根据式(16)，在图7中得到了3-P(4S)振动台在初始高度平面(zp=0)内，1阶固有频率对各结构参数的灵敏度的位置变化图。

由图7可以看出，3-P(4S)振动台在初始位置(xp=0,yp=0,zp=0)对各结构参数的灵敏度最小，而越靠向运动空间的边缘，其灵敏度则越来越大。而且，3-P(4S)振动台只对ra的1阶固有频率灵敏度是负值，对其他结构参数的1阶固有频率灵敏度均是正值，这说明机构的1阶固有频率同结构参数ra呈反向变化，同其他结构参数则呈同向变化。

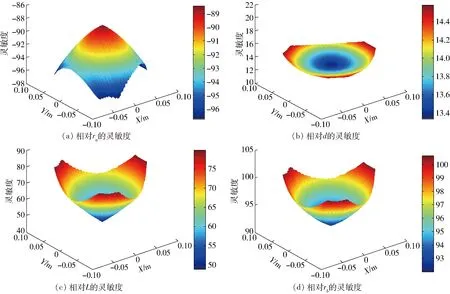
图7 1阶固有频率对结构参数的灵敏度Fig.7 Sensitivity of the first order natural frequency to structural parameters

由图7中还可看出，固有频率对ra和rb的灵敏度高于对d和L的灵敏度，这说明ra和rb对机构的低阶振动特性的影响更大，因此在实验过程中，如果机构的固有频率不符合工作条件要求，改变机构上下平台的结构尺寸可以达到更好的效果。

3 模态实验

模态实验主要对机构进行激振测试，应用传感器对激励信号以及振动响应信号进行采集并处理，将信号输入模态分析软件中，得到系统的振动特性。模态测试包括激励系统、测试系统及分析系统[20]。

激励系统的激励形式有稳态正弦激励、随机激励和脉冲激励，为了节约成本，提高实验效率，选择脉冲激振形式。通过带有力传感器的冲击力锤进行敲击，以施加给振动台宽频脉冲信号，从而实现脉冲激励，进而激发振动台的各阶模态。

测试及分析系统主要包括力传感器、加速度传感器以及计算机分析系统，其中力传感器可用来采集激励信号，加速度传感器可用来采集拾振点的振动响应信号。传感器将采集到的模拟量信号通过电荷放大器、数据采集卡输送到计算机，计算机通过数据处理，得到各阶幅频特性曲线，从而得到机构各阶固有频率。模态测试步骤框图如图8所示。所搭建的模态实验系统如图9所示。

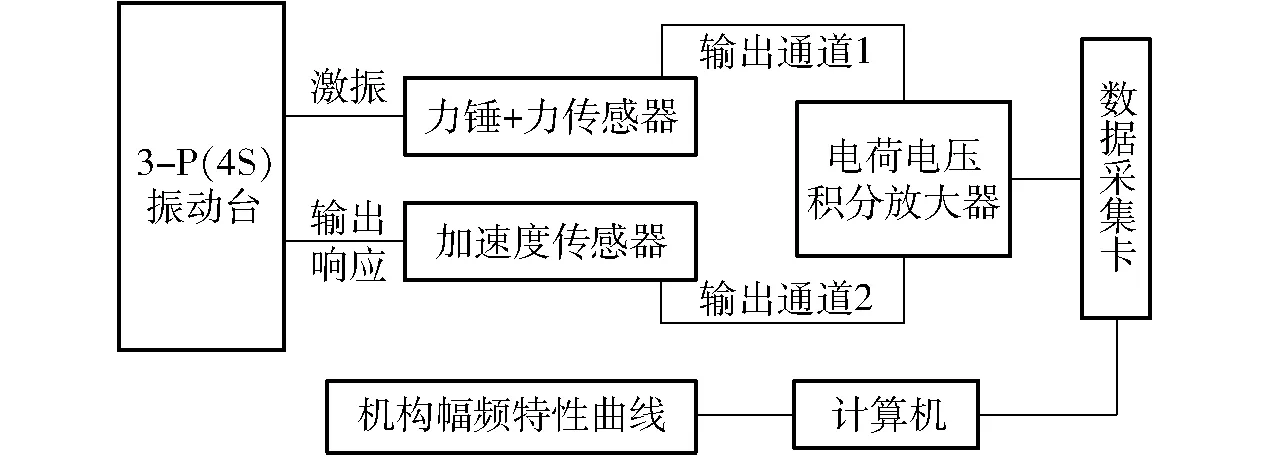
图8 振动台模态实验框图Fig.8 Modal experiment diagram of vibration platform

图9 模态实验平台Fig.9 Experimental platform of modal1.计算机 2.数据采集卡 3.控制柜 4.带力传感器的力锤 5.加速度传感器 6.3-P(4S)振动台 7.电荷放大器

实验选用LC-1型电荷式模态力锤，其灵敏度为4.74 pC/N，适用范围为0～5 kN，整体由锤体、锤帽以及力传感器组成。加速度传感器型号为YD81D电荷输出型，安装在上平台的螺纹孔内，灵敏度为1.39 pC/(m·s-2)，其谐振响应频率为27 kHz，远高于测试频率，可满足实验要求。

对于电荷型加速度传感器所接的SD1436型电荷电压积分放大器，需将拨码开关上的数值设定成传感器的灵敏度，并将功能转换器设定为输出加速度，采用低通滤波模式，并将输出数值设为1 mV/(m·s-2)，然后，所采集到的电压模拟量即可作为振动加速度。

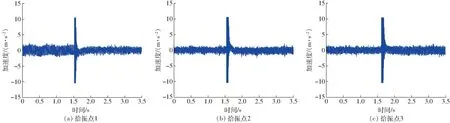
图12 输出响应的时域波形Fig.12 Output response time domain waveform

最后数据采集卡选用USB-1608G十六位数据采集卡，模拟量信号通过USB接口传给计算机，计算机经数据处理后得到振动分析结果。

上平台激振点以及拾振点的位置布置如图10所示，由于振动台具有分别沿坐标轴X、Y、Z方向的模态，所以需要在每个模态方向上分别进行一次敲击测试。图中激振点1、2、3代表着力锤敲击点的位置和方向，拾振点1、2、3则为加速度传感器的布置位置及方向，拾振点处有螺纹孔，可将加速度传感器旋入安装。由于上平台呈六边形结构，所以对Y轴模态测试的激振点和拾振点不好布置，因此选择六边形两组对应的邻边作为X轴和Y轴的激振点和拾振点的布置位置。

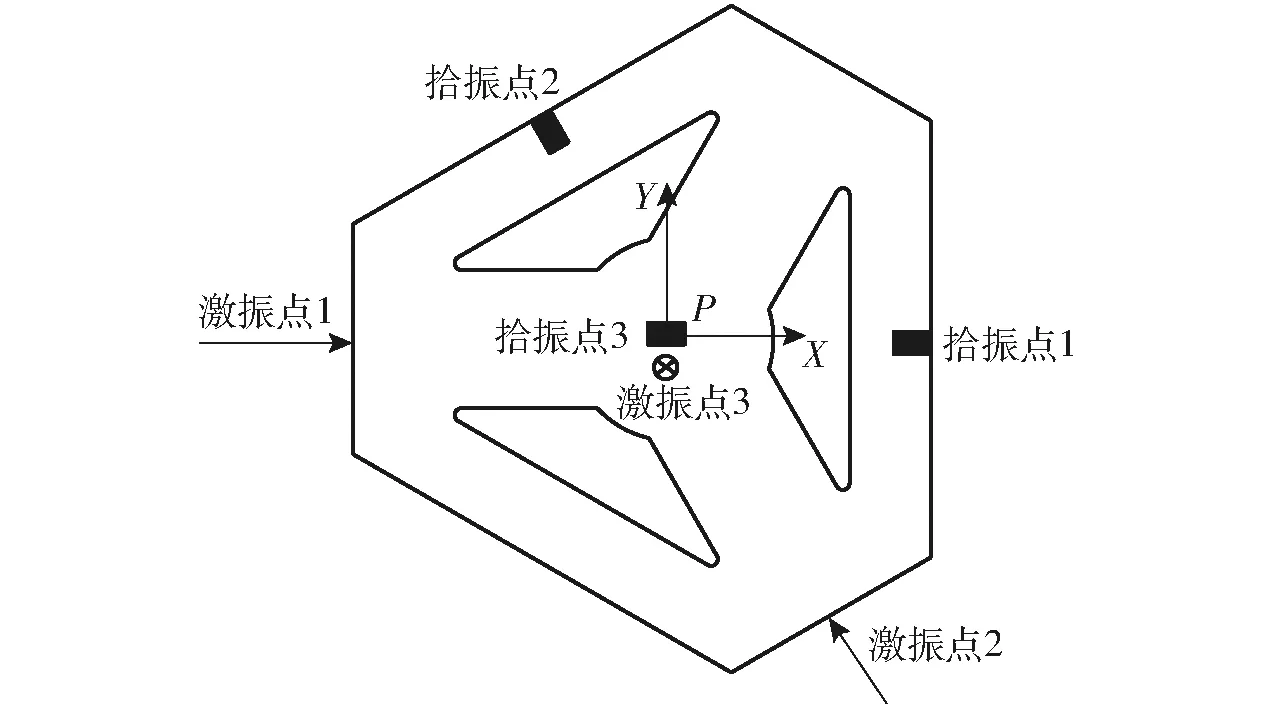
图10 激振点以及拾振点布置Fig.10 Layout of exciting point and vibration point

测定的是机构在初始位置(X=0,Y=0,Z=0)下的各阶模态参数，因此测试前需将机构调整到0位，分别沿激振点1、2、3进行敲击测试，每个激振点测定3次，然后应用LabVIEW软件采集每次测试的输出信号。图11为机构沿X轴方向的敲击模态实验过程。

图11 沿X轴方向的模态敲击测试Fig.11 Modal strike test along X direction

对测得的加速度传感器的信号进行处理，可得振动台输出响应加速度的时域波形，共得3组，图12所示为其中1组，由于实际中阻尼的存在，响应会逐渐衰减。

对3组时域信号分别进行傅里叶变换，然后求其平均值，可得到输出响应的频谱图，如图13所示。

将实验结果和理论计算结果对比分析，由表4可知，理论与测定结果存在误差，其原因有：理论模型的建立中忽略了阻尼以及非线性因素的影响；在实验过程中，传感器的测量以及频谱分析都存在一定的误差，但总误差在3%以内，从而验证了理论计算过程的正确性。

本实验并未应用力锤的激励信号，因为本次实验是为了验证固有频率的理论求解，以确保共振频率高于工作频率范围，通过对振动输出响应的处理，并得到响应频谱图即可实现。应用力锤的激励信号可求得系统传递函数，并对振动台进行模态参数识别，本实验系统的搭建为其奠定了基础。

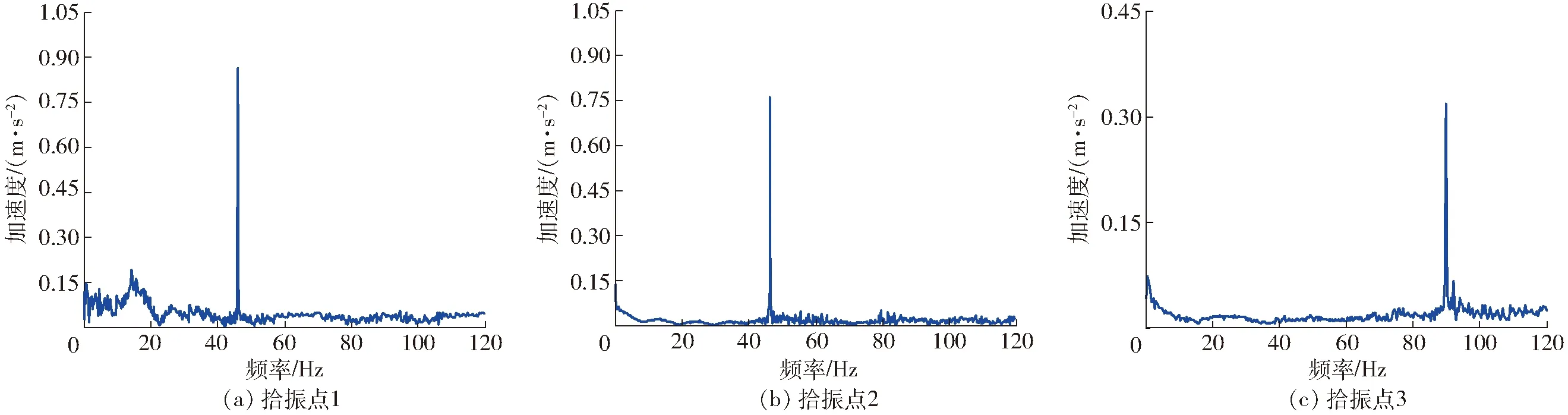
图13 输出响应的频域波形Fig.13 Output response frequency domain waveform

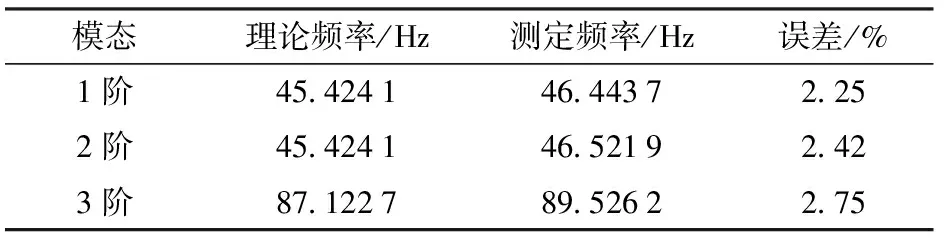
表4 理论与实验结果比较Tab.4 Contrast of theory and experiment results

4 结束语

对3-P(4S)振动台的振动特性进行了深入分析，首先建立了机构的简化振动模型，并应用仿真软件进行验证，其误差在0.5%以内。然后对机构的固有频率随运动位置变化特性以及灵敏度特性进行了具体分析。最后进行了3-P(4S)振动台的模态实验。通过比较，振动台的固有频率的实验测定值与理论计算值的误差均在3%以内，从而证明了理论模型的正确性，对3-P(4S)机构的实际应用提供了可靠的基础。