生物炭对东北草甸黑土水分运动参数的影响

王睿垠 魏永霞 刘 慧 张翼鹏 马德才 李冠奇

(1.东北农业大学理学院，哈尔滨 150030； 2.东北农业大学水利与土木工程学院，哈尔滨 150030；3.农业部农业水资源高效利用重点实验室，哈尔滨 150030； 4.中山大学中法核工程与技术学院，珠海 519082；5.中铁西南科学研究院有限公司，成都 611731)

0 引言

生物炭是一种稳定的碳化合物，是生物质在缺氧及300～1 000℃温度下的热解产物[1]。已有研究报道，用生物炭作为土壤改良剂，可以改善土壤的某些特性和功能[2]。生物炭具有多孔性，因此在土壤中添加生物炭可以改善土壤物理性质，包括孔隙大小分布、总孔隙度、土壤容重、土壤含水率及导水率等[3]。

有研究者认为，生物炭作为土壤改良剂引起土壤物理性质的改善，直接原因是生物炭的多孔性。但文献[4]表明，大多数生物炭中95%的孔隙直径小于0.002 μm，生物炭的自身孔隙增加了土壤1×105～1×107cm基质吸力的持水量，从而潜在地增加了土壤中直径范围在0.000 3～0.03 μm的孔隙数量；同时注意到，大多数植物不能从小于0.2 μm(低于永久枯萎点15 000 cm)的孔隙中提取土壤水，故生物炭的自身孔隙不能提高土壤的持水量。有研究认为，在土壤中添加生物炭，会在生物炭颗粒和土壤团聚体之间形成适应性孔隙[5]，孔隙的大小和比例受土壤团聚体的大小、生物炭颗粒的大小、土壤压实程度以及土壤固结的影响，但以上影响因素缺乏有效证据[6]，因此添加生物炭的土壤具有较高总孔隙度的原因还没有确切结论。

土壤水影响着植物和土壤生物的生存状况，土壤导水率是土壤的重要参数，决定了土壤中水分渗透的快慢、产生径流的大小[7]，影响着地表水的存储以及植物的可利用水，所以研究生物炭对土壤水力特性的影响对农业尤为重要。有研究证明，将生物炭添加到土壤中，可以提高土壤含水率[8]，增加作物的产量[9-11]，提高植物可利用的有效水[12-13]，改变土壤疏水性[14]以及改变土壤的水力学特性[15-17]。还有研究表明，添加生物炭，会导致沙土的导水率变小[18]、黏土的导水率变大[19]。受制备生物炭的原料和热解温度的影响，关于不同质地的土壤中添加不同量的生物炭对土壤导水性的影响，很多学者未达成一致。尽管土壤的导水率对于农业土壤水的利用至关重要，但生物炭对土壤水力特性直接影响的研究大都集中在试验研究，且研究结论尚不一致[20-22]。

本文从简化的土壤几何模型出发，采用土壤的VAN GENUCHTEN模型推导出添加生物炭土壤的水分特征方程，说明生物炭对土壤水分特性的影响；采用MUALEM理论和利用水分特征方程推导添加生物炭土壤的相对导水率和水分扩散率方程。通过理论与试验数据比较，给出修正的添加生物炭土壤的水分特征方程和相对导水率方程。利用水平土柱吸渗试验，在室内条件下验证扩散率方程的准确性。同时，利用自然降雨数值模拟东北草甸黑土区坡耕地的降雨入渗，比较数值计算与田间试验的数据来验证理论推导的有效性，以期为理论及数值上研究添加生物炭土壤的水力学特性提供方法与保障。

1 材料与方法

1.1 研究区概况

研究地点为典型东北黑土区，位于黑龙江省农垦北安管理局红星农场试验基地(48°10′E、127°1′N)，坡度为3°～5°。该地区7—9月累积降雨量约402 mm，约占年平均降雨量的75%。该区域土壤以粗粉沙和粘粒为最多，各占30%～40%左右，透水、持水、通气性均较好，容重1.0～1.3 g/cm3，总孔隙度为40%～60%，通气孔隙度约20%，毛管孔隙为20%～30%。

1.2 试验材料与设备

供试材料为购自辽宁金和福农业开发有限公司的玉米秸秆生物炭，在450℃无氧条件下高温裂解。基本理化性质为：2 mm粒径约占60%以上，密度约为596 kg/m3，pH值为9.28。全碳质量分数72.21%，全氮质量分数1.56%，全磷质量分数0.72%，全钾质量分数1.64%。

采用CR-21G3型高速离心机，其脱水面半径为9.8 cm，用离心机在室内测定水分特征曲线；自制有机玻璃筒，长80 cm、直径8 cm，玻璃筒表面距供水端10、20、30、40、50、60、70 cm处有取土孔，用于取出不同位置的土壤，可测得各位置的含水率；采用TRIME-T3型管式土壤水分测量系统(TDR)进行田间土壤含水率的测量。

1.3 试验方法与内容

2017年5月中旬将生物炭均匀混入黑土耕层(0～20 cm)。田间试验地块面积为5 m×20 m，取样时间为2017年9月。设置5种处理：不添加生物炭处理(CK)和生物炭分别占土壤的体积比为2%(C1)、4%(C2)、6%(C3)、8%(C4)。

沿径流小区纵向每隔6.5 m用环刀采样器取各处理的原状土样，取土深度10～15 cm、环刀体积100 cm3、高5 cm。为消除生物炭的疏水性，将购买的生物炭(BC)放置田间4个月后再进行试验。用蒸馏水将各处理土样和生物炭吸水48 h，吸至饱和后称量。称量后在环刀上放置滤纸和环刀底盖，用离心机法测定土壤和生物炭的水分特征曲线。离心机转速设定为500～6 000 r/min，离心时间100 min[23]，离心结束后称量。各处理土壤与生物炭各重复3次。

用定水头法在室内测定5种处理的饱和导水率，试样为用环刀采样器取出的各处理原状土样。维持马氏瓶供水水头恒定为5 cm，每隔10 min记下出流水量，直到出流水量稳定后，结束试验。根据测得的数据计算饱和导水率，各处理重复3次。

采用水平入渗法测量土壤水分扩散率。水平入渗法是测定土壤水分扩散率的非稳定流法，该方法利用水平土柱吸渗试验数据，结合解析方法计算出土壤水分扩散率。采用BOLTZMANN变换，ξ=xt-1/2，其中ξ为BOLTZMANN变换参数。对一维水平流动微分方程求解，得

(1)

式中D(θ)——土壤水分扩散率，cm2/min

θa——初始土壤含水率，cm3/cm3

θ——土壤含水率，cm3/cm3

通常将式(1)转换为差分的形式，表达式为

(2)

水平土柱试验装置示意图如图1所示。在5个处理小区取原状土样，取土深度为10～15 cm，风干后碾碎磨细，过2 mm筛，按田间实测容重分层回填入有机玻璃筒。每层3 cm，层与层之间的接触面打毛，回填高度共80 cm。开启马氏瓶供水阀门，记录起始时间，湿润锋移至土柱70 cm处停止供水，记录结束时间。供水停止后迅速从有机玻璃柱间隔为10 cm的取土孔取土，取至湿润锋所在位置。测定相应位置的土壤容积含水率，每个处理重复3次，再由式(2)计算土壤的水分扩散率。

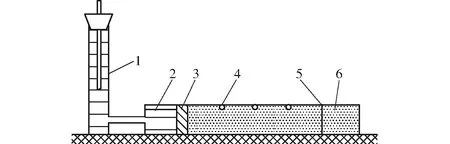
图1 土壤水分扩散率试验装置示意图Fig.1 Schematic of experimental setup for measuring soil water diffusivity1.马氏瓶 2.水室 3.滤层 4.取土孔 5.湿润锋 6.水平土柱

2017年8月9日研究区自然降雨后，测定田间土壤不同时间和不同深度含水率。降雨时长10 h，降雨总量15 mm，降雨30 h后每隔20 h用TDR测各小区深度10～15 mm处的含水率；降雨20 h和120 h后用TDR测量各小区深度为0.15、0.3、0.6、0.8、1 m处土壤的含水率，重复测量3次。

1.4 数据处理方法

采用Microsoft Excel 2010进行数据计算整理，采用Retc软件进行水分特征曲线的拟合，采用Matlab进行数值计算和数据可视化，采用限元分析软件Abaqus 6.13进行数值模拟计算。

2 添加生物炭土壤的水力特性分析

2.1 水分特征曲线

根据试验分别测定土壤和生物炭的水分特征曲线，将生物炭按不同比例添加到土壤中，通过计算可以得到添加生物炭土壤的水分特征曲线。计算添加不同比例生物炭土壤的水分特征曲线几何模型如图2所示。

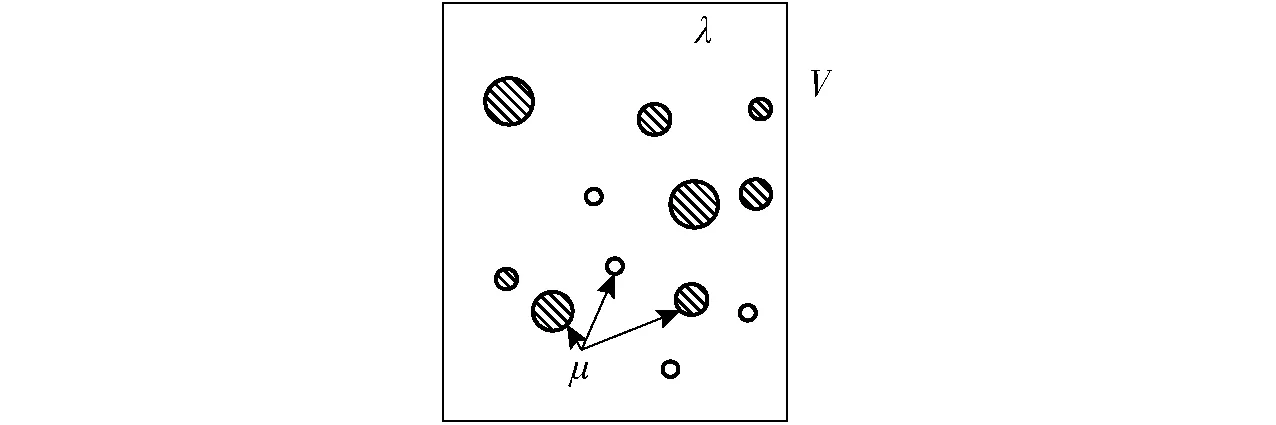
图2 添加生物炭的土壤模型Fig.2 Soil model of added biochar

设添加生物炭土壤中土壤的体积比为λ，生物炭的体积比为μ，λ+μ=1。当生物炭和土壤混合对应的基质吸力为h时，体积为V的土壤总含水量为

Q=λVθ1+μVθ2

(3)

式中θ1——对应基质吸力为h的土壤含水率

θ2——对应基质吸力为h的生物炭含水率

这时添加生物炭土壤的含水率为

(4)

当添加生物炭土壤饱和时，土壤和生物炭都处于饱和状态，此时添加生物炭土壤的饱和含水率为

θs=λθ1s+μθ2s

(5)

式中θ1s——土壤饱和含水率

θ2s——生物炭饱和含水率

同理，添加生物炭土壤的残余含水率为

θr=λθ1r+μθ2r

(6)

式中θ1r——土壤残余含水率

θ2r——生物炭残余含水率

当基质吸力为h时，添加生物炭土壤的饱和度为

(7)

如果θ1s-θ1r和θ2s-θ2r相差不大，可近似看作相等，式(7)中各项除以(θ1s-θ1r)，并考虑到λ+μ=1，得

(8)

式中Θ1——土壤饱和度

Θ2——生物炭饱和度

VAN GENUCHTEN[24]在1980年提出了土壤水分特征曲线(SWCC)的模型。该模型给出土壤的饱和度和基质吸力的关系为

(9)

其中

m=1-1/n(n>1)

式中α、n、m——曲线拟合参数

本研究采用VAN GENUCHTEN模型，如果土壤和生物炭都满足式(9)的模型，则式(8)可以写成

(10)

式中α1、n1、m1——土壤拟合参数

α2、n2、m2——生物炭拟合参数

如果测得土壤和生物炭的各个参数，就能由式(10)推导出添加生物炭土壤的饱和度。又式(10)不能简化为单一的指数形式，因此添加生物炭土壤的饱和度不能采用单一的VAN GENUCHTEN模型，而只能是叠加形式。如果已知土壤和生物炭的饱和度，通过式(10)就能给出添加生物炭土壤的饱和度。

采用式(5)和式(6)，并根据

θ=(θs-θr)Θ+θr

(11)

给出添加生物炭土壤的含水率，进而得到添加生物炭土壤的水分特征曲线。

2.2 非饱和导水率

土壤的非饱和导水率不仅难测定，而且测量数据的准确度也较难保证。因此，很多学者推荐采用非直接的方法来估计土壤的非饱和导水率[24-25]。其中，利用较容易测得的土壤水分特征曲线，来推测非饱和导水率是最常用的方法。MUALEM[25]用水分特征曲线来预测土壤的相对导水率，采用的公式为

(12)

其中

Θ0=Θ(h0)

式中Θ0——基质吸力为h0时的饱和度

Kr(Θ0)——基质吸力为h0时的相对导水率

f(Θ0)——以水分特征曲线为变量的函数

确定了基质吸力和饱和度关系，可以采用式(12)得到土壤的相对导水率，再根据

K=KsKr

(13)

式中Ks——土壤的饱和导水率

K——土壤的非饱和导水率

得到土壤的非饱和导水率。

由于式(10)分成两项，式(12)中f(Θ0)不能直接写成显式形式，把函数进行变量替换，f(Θ0)描述为

(14)

式中Θ1(h0)——基质吸力为h0时土壤饱和度

Θ2(h0)——基质吸力为h0时生物炭饱和度

吸力作为饱和度的函数，可以采用不同的参数，同一土壤内，生物炭和土壤的饱和度虽然不同，但基质吸力是一样的，即h(Θ)=h(Θ1)=h(Θ2)。利用式(9)和式(10)给出

(15)

式(14)中的第1项可以写为

(16)

式(16)中采用变量代换，Θ1=ym1。因为式(16)的积分项是不完全的BETA函数，只有m1-1+1/n1为整数时，积分才有值。当m1-1+1/n1=0时，式(16)变为

(17)

将式(17)代入式(14)得

(18)

将式(18)和式(8)代入式(12)，可得

(19)

根据式(8)和式(10)有

(20)

2.3 水分扩散率

式(1)中土壤水分扩散率的基础是一维土壤水分运动的BOLTZMANN变换解，本文理论上采用水分特征曲线给出水分扩散率。理论上

(21)

将式(19)和式(20)代入式(21)得到水分扩散率为

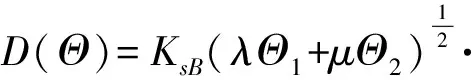
(22)

式中KsB——添加生物炭土壤的饱和导水率

3 结果与分析

3.1 生物炭对土壤物理性质的影响

不同处理土壤的物理性质如表1所示。土壤容重随生物炭的增加呈下降趋势，土壤的饱和含水率和饱和导水率随着生物炭的增加而增加。这表明施加生物炭会增加土壤的总孔隙度，这和已有的研究结果[3]一致。

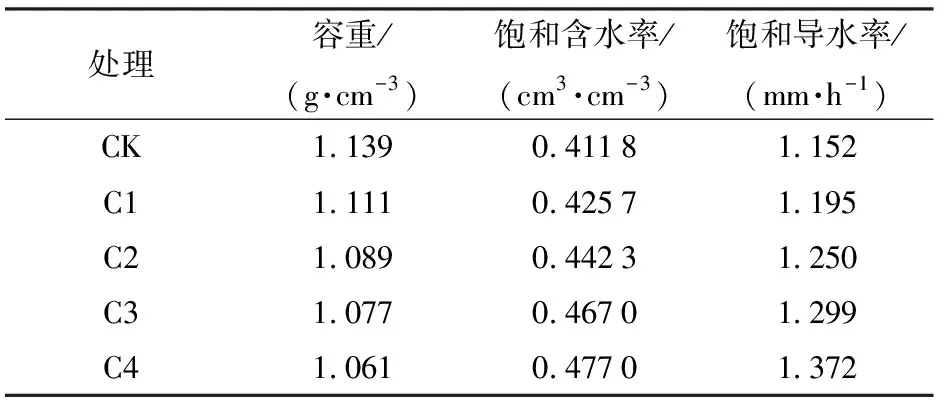
表1 不同处理土壤的物理性质Tab.1 Physical properties of soil for different treatments

3.2 土壤水分特征曲线

用离心机法分别测得土壤和生物炭的水分特征曲线如图3所示。

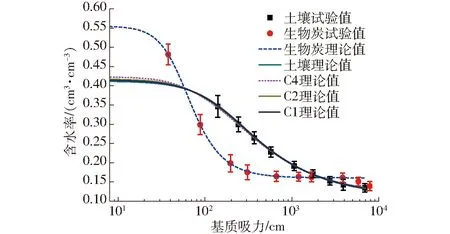
图3 土壤与生物炭水分特征曲线的试验和理论计算值Fig.3 Measured and theoretically calculated values of soil and biochar characteristic curves

采用VAN GENUCHTEN模型，利用Retc软件对离心机法实测的土壤水分数据进行拟合，拟合的饱和含水率为0.411 8 cm3/cm3、残余含水率为0.107 8 cm3/cm3、参数α1为0.006 18、n1为1.666 7。农业土壤的基质吸力一般在中低段，在中低吸力段拟合生物炭的饱和含水率为0.555 cm3/cm3、残余含水率为0.16 cm3/cm3、参数α2为0.018 8、n2为2.797 9。根据式(9)拟合的曲线如图3所示，由于曲线较密集，C3的数据没有在图中显示。

根据式(5)、(6)以及式(10)、(11)，利用拟合的参数，采用Matlab计算的C1、C2、C4的水分特征曲线如图3所示。试验测得的C1、C2、C4的数据如图4所示。

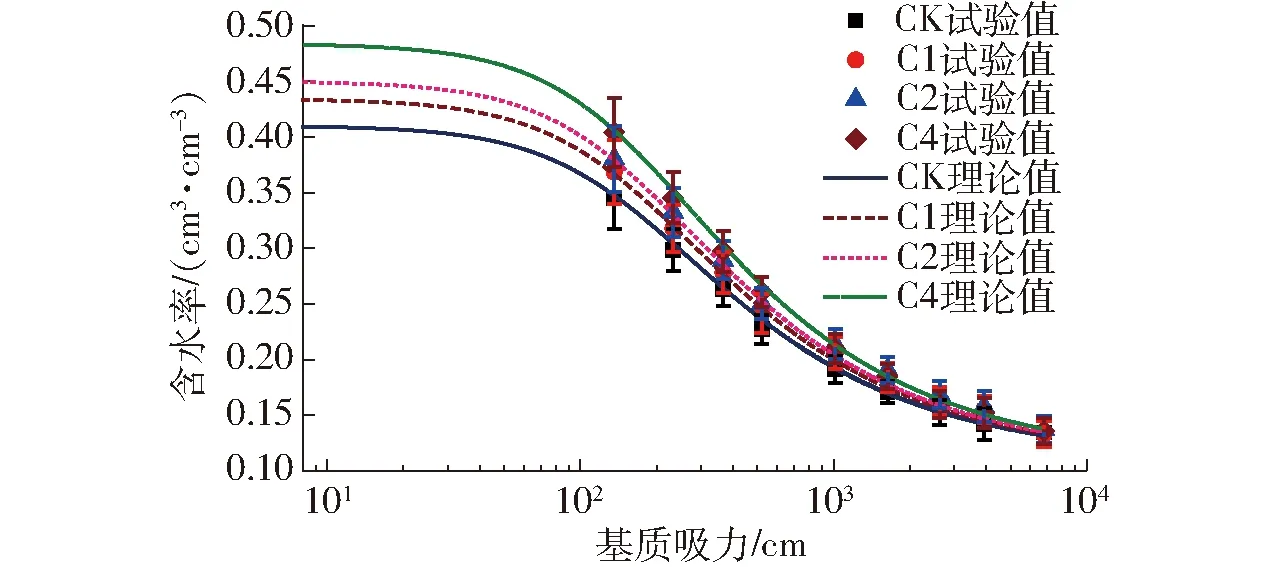
图4 添加生物炭土壤的水分特征曲线Fig.4 Soil water characteristic curves of soil that added biochar

比较图4的试验值和图3的理论值发现，在较低吸力下添加生物炭土壤含水率的试验值明显高于图3的理论值，这表明添加生物炭土壤与对照土样相比出现了较多空隙，进而提高了土壤的含水率。添加生物炭后土壤含水率提高的原因，不能是生物炭的孔隙直接引起的土壤孔隙度的增加，只能是生物炭与周围土壤团聚体之间的空隙或生物炭粒子之间的空隙引起的。

另外，在吸力较小时，添加生物炭土壤与无添加生物炭土壤相比，含水率随着添加炭的比例的增加而增加，这与理论和试验结果一致。但在中高吸力范围内，理论上添加生物炭的土壤应该比无生物炭添加土壤的含水率略低，实际测量结果却是添加生物炭土壤的含水率较高，这说明添加生物炭后土壤的结构发生了改变。基质吸力小于2 000 cm时，添加生物炭土壤的含水率显著提高；而基质吸力高于8 000 cm时，含水率变化不明显。从图4还可以看到，随着吸力的增加，添加生物炭土壤的曲线较理论值平缓，添加生物炭土壤的含水率较理论值下降得慢，说明土壤颗粒对生物炭发生作用即吸力增加时，生物炭中的水较难排出，这是因为当生物炭添加量较少时，生物炭颗粒被土壤团聚体包裹，水分随基质吸力的变化特性更接近无添加的土壤。式(10)推导过程中，没有考虑到土壤团聚体对生物炭的作用。如果添加生物炭土壤的饱和度随基质吸力的变化更接近无添加的土壤，则有

(23)

添加生物炭土壤的含水率就可以表达为

θ=(θs-θr)Θ1+θr

(24)

采用试验测得5个处理的饱和含水率，再根据式(9)和式(24)，可以给出不同生物炭添加量土壤的水分特征曲线，得到的理论曲线如图4所示。从图4可以看出，基质吸力小于1 000 cm时，式(24)能很好地描述添加生物炭土壤的水分特征曲线。图4中土壤水分特征曲线的理论值和试验值的最大误差出现在C4处理的7 780 cm吸力处，含水率的理论值和试验值分别为0.164 4、0.159 9 cm3/cm3，误差为3.2%。

3.3 土壤水分扩散率

用式(22)计算土壤水分扩散率，需采用式(24)计算出的含水率以及添加生物炭土壤的饱和导水率。实际测量CK、C1、C2、C4的饱和导水率如表1所示。为消除吸力为零处扩散率过大的影响，计算的吸力初始值取为5 cm。采用水平入渗法测定含水率，利用式(2)计算出土壤水分扩散率与含水率的关系如图5所示。

图5 土壤水分扩散率与含水率的关系Fig.5 Relationship between soil water diffusivity and water content

由图5可知，在含水率较低的区域，扩散率的试验数据比计算值略大，说明理论分析缺少生物炭与土壤团聚体间的空隙对土壤水分扩散率影响的考虑。由图5可知，理论分析仍能较准确地给出添加生物炭的比例对扩散率的影响。理论上在同一容积含水率的条件下，添加的生物炭比例越高，水分扩散率越小，这说明较多的生物炭能够抑制土壤水分的水平扩散。

4 自然降雨入渗条件下的数值模拟

为验证前述理论的准确性，进行了自然降雨条件下的数值计算和试验测定。数值计算采用分析软件Abaqus进行仿真。软件采用达西(DARCY)定律和质量守恒定律计算水分流动，对于二维问题垂直方向(y)的入渗，非饱和土壤水运动的基本微分方程为

(25)

其中

式中kx、ky——x和y方向的相对导水率

ks——各向同性的饱和导水率

Q1——施加的边界流量，为降雨量

Cw——容水度，由式(20)给出

γw——水的重度

对于非饱和土，kx和ky为基质吸力的函数，需要给定相对导水率函数，这里由式(19)给出。

根据东北典型的坡耕地地貌，采用的降雨入渗模型如图6所示，坡度为5°左右，添加生物炭土壤在上表面，厚度为20 cm。

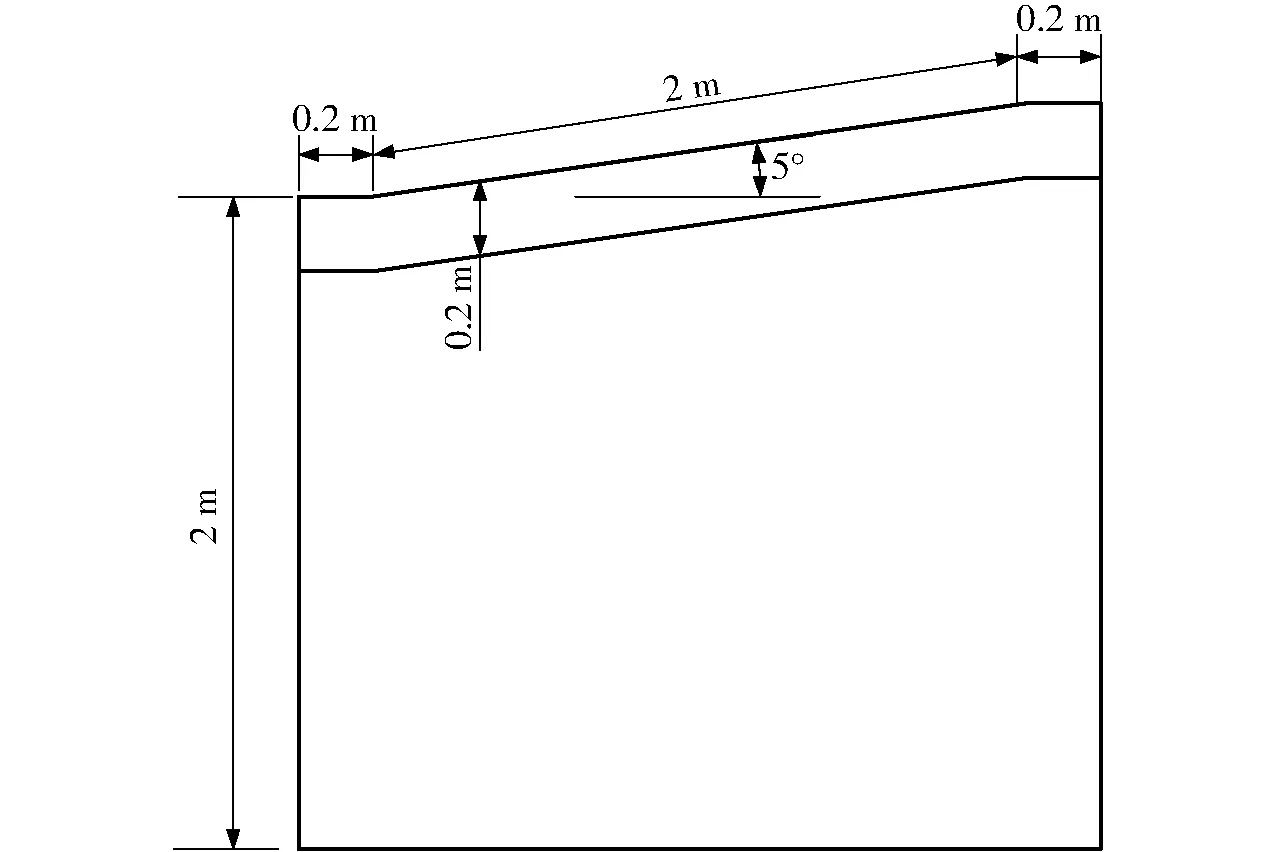
图6 计算降雨入渗模型简图Fig.6 Sketch of rainfall infiltration model

计算时采用的土壤水分特征曲线、相对导水率与含水率的关系曲线由式(10)、(11)、(19)给出。计算时CK、C1、C2、C3、C4的饱和导水率见表1。测量土壤的初始容积含水率为0.31 cm3/cm3、饱和度为0.662 7、对应的基质吸力为230 cm。实测降雨时长为10 h、降雨量为15 mm，计算采用的降雨载荷为1.5 mm/h、降雨时间持续10 h，降雨后持续测量120 h。计算降雨120 h后土壤的饱和度分布如图7所示。

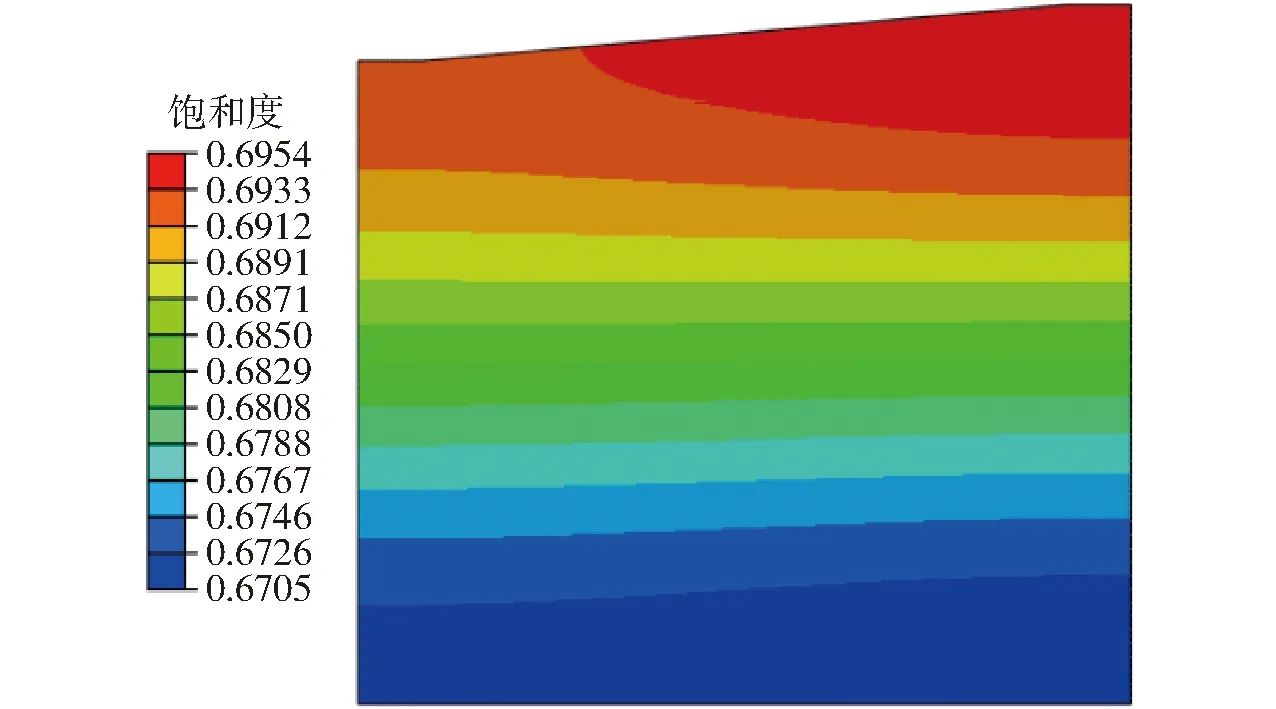
图7 降雨120 h后土壤的饱和度分布Fig.7 Soil saturation distribution after rainfall of 120 h

生物炭混入耕层土壤的厚度为20 cm，测量时考虑到表层土壤扰动大、蒸发作用明显，因此取10～15 cm处的土壤测量，以便较好地与计算值比较。计算结束后，取图7左边距离上表面15 cm处的含水率随时间变化值以及降雨后田间测量的含水率如图8所示。

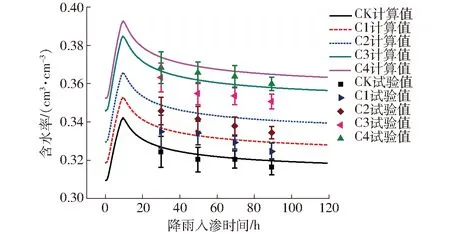
图8 降雨入渗的含水率计算值和试验值Fig.8 Calculated and measured data of soil water content after rainfall infiltration

从图8可以看到，田间测定的曲线落在计算值曲线的下方，即田间测得的数据整体比计算值偏低。二者不能完全吻合的原因为：①数值计算采用的数据都是室内试验测定的，与田间实际土壤有差别。②计算时没有考虑田间土壤的固结产生的各向异性。③模型仅考虑了水的渗透，忽略了实际土壤中水渗透的流固耦合问题。田间测定值和理论值的最大误差出现在C3处理的90 h处，为4.1%(小于5%)，这说明数值计算和田间实际情况比较吻合。

模型左边距地面不同深度的含水率计算值、降雨后20 h和120 h测量各生物炭处理小区不同深度的含水率如图9所示，由于曲线较密集，C3的值没有在图中显示。

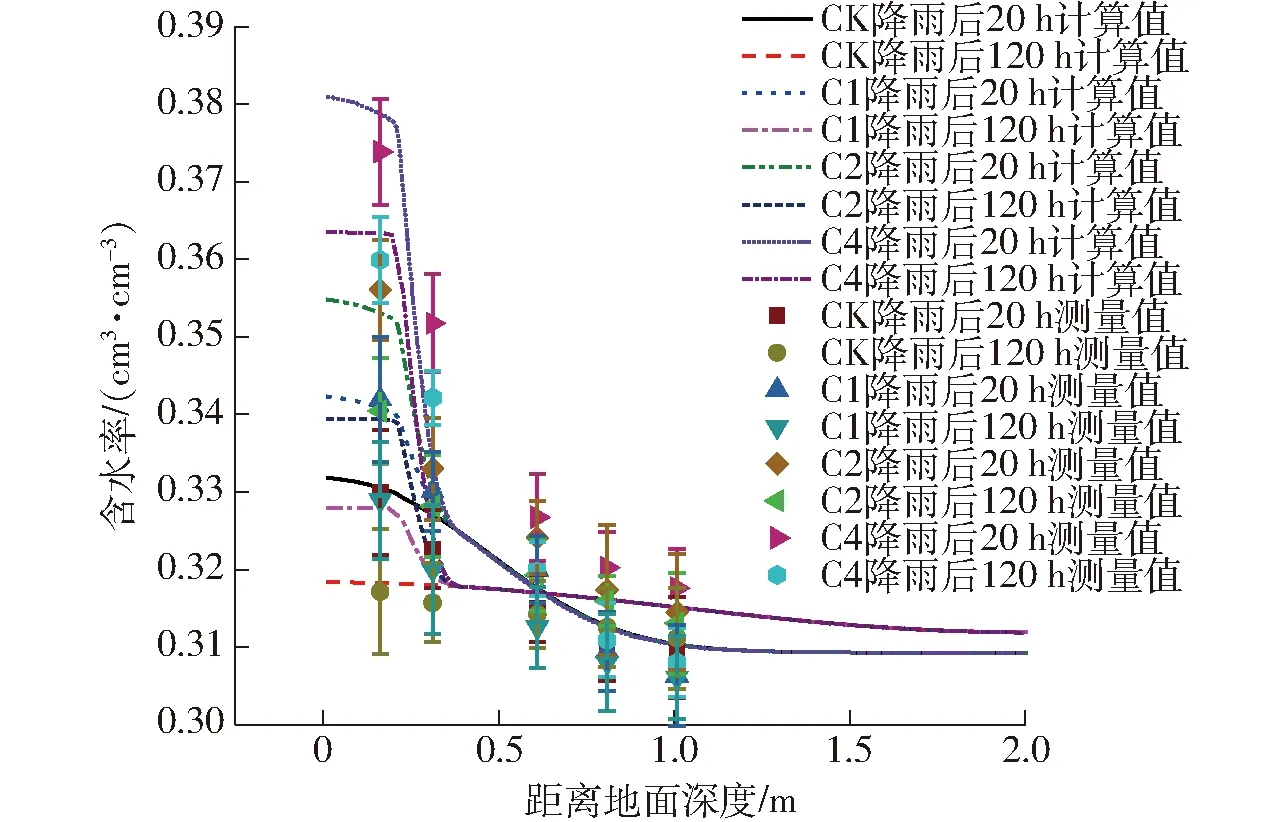
图9 含水率随距离地面深度变化的计算值和试验值Fig.9 Calculated and measured data of soil moisture content changed with depth

由图9数值计算的结果看，降雨后添加生物炭土壤的含水率随添加量的增大而增加。此外，随着土壤深度的增加，添加生物炭土壤层对底层土壤的含水率的影响很小，只有添加了生物炭的土壤层含水率才会增加。田间测得含水率分布的趋势与数值计算的结果基本一致。此外，降雨后底层土壤的含水率比数值计算结果偏高，这是因为数值分析采用的土壤特性数据是在室内理想状态下测定的。由于田间土壤的复杂性，如土壤中动植物活动以及农业作业的影响，使得田间底层土壤的测量值与实际产生偏差。数值分析的结果大体上和实际测量值吻合，在测量的深度范围内，数据的最大偏差为13.3%。

5 讨论

水分是农业生产的重要因素，许多研究把生物炭作为土壤改良剂来改善土壤的水力特性，目前针对生物炭改良土壤的研究多为试验研究，生物炭对土壤水分运动的影响尚不十分明确。试验研究较为复杂且不具有共性，如采用了非农业土壤[26]、使用木炭[27]、添加不切实际的高比例生物炭[28]、采用自己配比的土壤而非原状土[29]等。另外，很多研究结果只针对特定的土壤环境和特定的生物炭材料，鲜有生物炭对土壤水分影响的理论研究以及添加生物炭土壤水力特性的原理性分析。

土壤的理论模型研究较为广泛也比较成熟，本研究针对东北黑土区的草甸黑土添加生物炭，利用VAN GENUCHTEN土壤模型，推导出施加生物炭后的土壤水分特征曲线，利用MUALEM理论预测土壤的相对导水率。经分析发现，添加生物炭的土壤不完全满足VAN GENUCHTEN土壤模型，却与多孔隙土壤模型更加类似[30]。研究认为生物炭在土壤中的施加会在生物炭颗粒和土壤团聚体之间形成空隙，从而影响土壤的水分特征曲线。本研究试验数据表明，生物炭粒子和土壤团聚体之间会产生大量空隙，因此试验测得的添加生物炭土壤的含水率高于忽略了空隙的理论模型。

试验还发现，生物炭粒子被土壤团聚体包围，在中低基质吸力范围内，添加生物炭土壤饱和度与无添加的土壤相似，所以多孔隙土壤模型并不准确，添加生物炭草甸黑土的水分特征方程需要修正，修正后的方程在中低吸力范围内能够和试验数据相吻合。

本研究修正了土壤水分特征方程，推导了添加生物炭土壤的相对导水率方程以及水分扩散率方程。通过比较5种添加生物炭处理的水分扩散率的理论与试验数据，结果显示推导的理论结果能够较好地给出添加生物炭土壤的导水特性。在含水率较低即基质吸力较高时，添加生物炭土壤的水分扩散率理论值比实际测量值略低，主要是由于理论模型中没有考虑空隙对导水率的影响。

本研究采用有限元软件数值计算了添加生物炭土壤的降雨入渗问题，通过比较数值计算与田间实测数据来验证理论的准确性。结果显示，本研究给出的理论准确、有效，因此能为不同土质施加生物炭后的水力特性研究提供更多的方法与依据。

6 结论

(1) 比较理论分析和试验给出的添加生物炭土壤的水分特征曲线发现，土壤基质吸力小于2 000 cm时，添加生物炭会提高土壤的含水率；在高于8 000 cm的基质吸力时，添加生物炭不一定提高土壤的含水率。

(2) 试验证实了生物炭粒子会被土壤团聚体包裹，使得添加生物炭土壤的饱和度随基质吸力的增加而变化缓慢，在中低基质吸力区域，饱和度的变化更接近无生物炭添加的土壤。

(3) 添加生物炭后土壤含水率提高的原因，不是生物炭自身孔隙引起的土壤孔隙度的增加，应该是生物炭与周围土壤团聚体之间的空隙或生物炭粒子之间的空隙引起的。

(4) 理论分析和试验数据表明，施用生物炭能够抑制东北草甸黑土水分的水平扩散。

(5) 生物炭在土壤中的体积比小于8%时，降雨入渗的数值分析结果和田间实测的误差小于13.3%，本研究结果可为土壤水分运动参数数值计算提供依据。