遥感图像信号不相关随机噪声去除方法研究
刘雪峰 王聪聪 张现军


摘 要: 遥感图像无论在获取还是在传输中都会受到噪声的干扰,影响图像质量和进一步的数据挖掘。因此,在一般数字图像去噪算法的基础上探讨了对遥感图像信号不相关随机噪声的去除方法。由于小波变换理论在图像去噪处理中的应用广泛且效果显著,在此着重研究基于小波变换的小波阈值去噪算法。进而在coif3小波函数下进行仿真实验,结合仿真结果比較硬阈值和软阈值对噪声滤除的效果,同时还在软阈值的基础上尝试了多级软阈值去噪算法。实验结果表明,软阈值处理后的去噪效果要优于硬阈值,而多级软阈值处理后的效果优于纯软阈值处理的效果。
关键词: 图像去噪; 遥感图像; 信号不相关随机噪声; 小波变换; 小波阈值; 去噪效果
中图分类号: TN911.73?34; TP391 文献标识码: A 文章编号: 1004?373X(2018)14?0062?04
Research on signal?independent random noise elimination method for
remote sensing images
LIU Xuefeng, WANG Congcong, ZHANG Xianjun
(School of Automation & Electronic Engineering, Qingdao University of Science & Technology, Qingdao 266000, China)
Abstract: The remote sensing image can be disturbed by noises during its acquisition or transmission, which affects the image quality and further data mining. Therefore, a signal?independent random noise elimination method for remote sensing images is discussed on the basis of the general digital image denoising algorithm. As the wavelet transform theory is widely applied in image denoising processing and has a significant effect, the wavelet threshold denoising algorithm based on wavelet transform is emphatically researched. The simulation experiment was carried out with the coif3 wavelet function. In combination with the simulation results, the noise?filtering effects of hard threshold and soft threshold were compared, and the multi?level software threshold denoising algorithm was tried on the basis of the software threshold. The experimental results show that the denoising effect of soft threshold processing is better than that of hard threshold processing, and the effect of the multi?level soft threshold processing is better than that of the pure soft threshold processing.
Keywords: image denoising; remote sensing image; signal?independent random noise; wavelet transform; wavelet threshold; denoising effect
0 引 言
遥感(Remote Sensing)是通过不与事物直接接触而得到事物信息的探测和感知,它是用传感器收集目标物的电磁波信息,并通过相应的计算机设备对所获得的数据进行整理分析得到其相关信息的一门自然科学技术[1]。遥感技术可以被看作是一个审阅和提取信息的过程,其核心技术的是通过各种传感器来对所要调查对象进行数据的收集和分析,以获得对该调查对象的相关信息。遥感数据的收集形式多种多样,可以通过光谱、电磁能量谱、以及声波等方式来收集。遥感技术具有大面积同步观测、时效性强、数据综合可比性强、经济与社会效益高的优点,在相关领域逐渐成为重要的技术支持,例如:地质找矿[1]、农作物的病虫灾害预测[2]、海洋资源勘测、检测大气分布[1]、军事目标的识别等。
遥感图像是通过各种传感器进行信息的收集,然后再经过电子设备的传输到达处理图像的计算机设备中。因此信号在获取和传输中会受到各种干扰,从而使得遥感图像受到噪声的污染,降低了图像的质量[3]。遥感图像中的噪声以随机噪声为主,主要分为信号相关随机噪声和信号不相干随机噪声两大类。其中信号相关随机噪声是由高光谱传感器中的光学器件的特性造成,这种噪声与信号具有很强的相关性。信号不相干随机噪声是由传感器中的电子元器件产生的,可以看作是一种加性噪声。本文主要讨论此类噪声的去除方法,下文中的噪声均指此类噪声。

遥感图像去噪的基本原理是通过将噪声和图像信号的能量信息进行分离,进而将噪声滤除并得到清晰度比较高的图像。国外在遥感图像去噪方面取得了很多的研究成果。其中最富有代表性和实用性的当数杜和维特利早年提出的Contourlet变换[2],不过该方法的局限性随着应用的深入也日益显露出来。随着数字图像处理和数字信号处理相关领域的继续发展,针对Contourlet变换的不足,很多研究者提出了改进措施,例如:库尼亚和M.N.Do提出了非下采样方法(NSCT)[2]等。
国内也有学者在对此方面进行了相关的研究。其中主要有:基于张量法的遥感影像的去噪算法[4?6]、双变量结构模型和 PDDFB 变换[7]、非局部均值和结构检测结合的遥感图像的去噪算法研究[8]等。小波变换法具有低熵性和多分辨率性质,可以很好地刻画图像非平稳特性,效果比较理想[9]。因此,基于上述理论本文着重讨论了基于小波变换的遥感图像去噪算法并进行了相应的仿真实验。
1 小波变换
1.1 连续小波变换
平方可积函数[f(t)∈L2(R)]的连续小波变换可以表示为[9]:
[Wf(a,b)≤f, ψa,b=1aRf(t)ψt-badt, a≠0]
(1)
[Wa,b(t)=1aψt-ba,]是由母小波生成的小波,[a,b∈R]且[a≠0],a为[f(t)]函数的伸缩子,b为平移因子。为了得出连续小波变换的重构公式,[ψ]需满足一定的容许性条件: [Cψ=-∞∞1ωψ(ω)2dω<∞,] 如果[ψ∈L(R)]是连续的,那么[ψ]可以推出重构公式为:
[f(t)=1Cψ-∞∞-∞∞1a2Wf(a,b)ψt-badadb] (2)
1.2 离散小波变换
离散小波变换(Discrete Wavelet Transform,DWT)[10]是指对参数a和参数b 进行离散化,而不是通常意义上对时间t离散化。在离散小波变换中如何在分析中降低计算量和数据量是研究小波变换的重要课题[11]。因为如果对尺度参数a和偏移参数b 离散的间隔选取较小,那么计算量和数据量都是非常大的。所以为了降低这两个变量通常,把尺度a和偏移b取作幂级数的形式,即:[a=am0,b=nb0am0,m,n∈Z]。这里,[a0]是固定值,為了方便起见,总是假定[a0>1],对应的离散小波[ψm,n(x)]公式为:
[ψm,n(x)=a-m20ψ(a-m0x-nb0), m,n∈Z] (3)
这时的小波函数就是离散小波。相应的小波变换为: [DWTm,n=-∞∞f(x)ψm,n(x)dx =f(x)ψm,n(x), m,n∈Z] (4)
二进制小波(Dyadic Wavelet)数学公式为:
[ψm,n(x)=2m2ψ(2-mt-n), m,n∈Z] (5)
式中,m和n分别表示频率范围和时间步长变化指数。从式(1)~式(5)可以看出,离散小波变换也具有同连续小波变换的时频分析的特性,它从某个区间上的基本函数开始,以基本波形的形式向左或向右移动特定的步长,并通过平移因子的扩张或压缩来构造函数集。
2 基于小波阈值的遥感图像去噪
小波分解可以将遥感图像分解为高频和低频部分,基于此在不同尺度上选择一个既能有效地去除噪声又能使图像有用信息保留完整的阈值。选取合适的阈值是比较困难的,会涉及数学中的概率估计等知识。目前对于一般的图像处理阈值选择中大多数人选择了英国多诺霍和约翰斯顿提出的统一阈值原则[12],[δ=σ2lnN],其中,[δ]为标准差,N为尺度。对于阈值的选取大于阈值的小波系数一般为低频信息,将其保留,小于阈值的小波系数则为高频噪声信息,将其小波系数置零,最后再对其进行小波反变换获得经过阈值去噪处理的遥感图像信号[13?14]。
本文根据噪声主要分布在图像的高频信息中这一特性,取噪声信息集中的高频区域来估计噪声的标准差,以标准差的估计值来代替整个图像的标准差,再通过统一阈值选择的算法计算出阈值的大小,进而实现图像的阈值去噪。同时在软阈值去噪的基础上尝试了多级软阈值去燥方法,即对噪声图像高频系数进行连续的多次阈值处理,从而获得更为清晰的遥感图像。
3 仿真实验
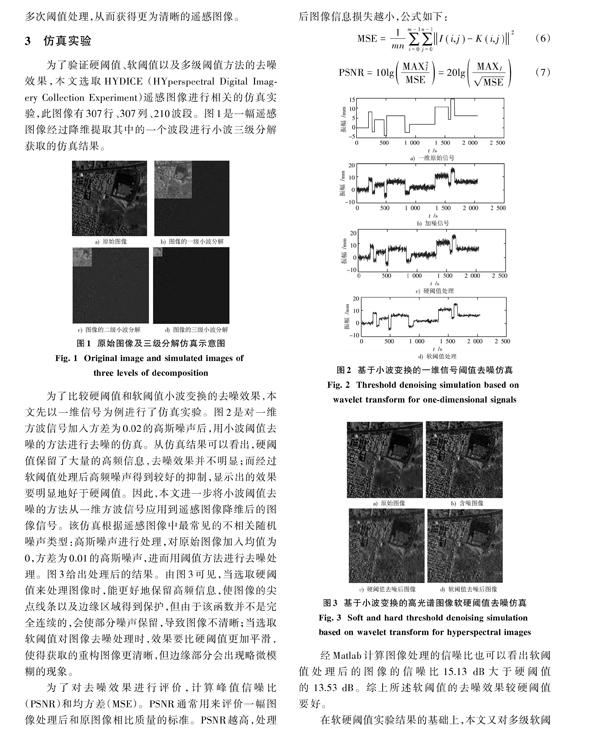
为了验证硬阈值、软阈值以及多级阈值方法的去噪效果,本文选取HYDICE (HYperspectral Digital Imagery Collection Experiment)遥感图像进行相关的仿真实验,此图像有307行、307列、210波段。图1是一幅遥感图像经过降维提取其中的一个波段进行小波三级分解获取的仿真结果。
为了比较硬阈值和软阈值小波变换的去噪效果,本文先以一维信号为例进行了仿真实验。图2是对一维方波信号加入方差为0.02的高斯噪声后,用小波阈值去噪的方法进行去噪的仿真。从仿真结果可以看出,硬阈值保留了大量的高频信息,去噪效果并不明显;而经过软阈值处理后高频噪声得到较好的抑制,显示出的效果要明显地好于硬阈值。因此,本文进一步将小波阈值去噪的方法从一维方波信号应用到遥感图像降维后的图像信号。该仿真根据遥感图像中最常见的不相关随机噪声类型:高斯噪声进行处理,对原始图像加入均值为0,方差为0.01的高斯噪声,进而用阈值方法进行去噪处理。图3给出处理后的结果。由图3可见,当选取硬阈值来处理图像时,能更好地保留高频信息,使图像的尖点线条以及边缘区域得到保护,但由于该函数并不是完全连续的,会使部分噪声保留,导致图像不清晰;当选取软阈值对图像去噪处理时,效果要比硬阈值更加平滑,使得获取的重构图像更清晰,但边缘部分会出现略微模糊的现象。

为了对去噪效果进行评价,计算峰值信噪比(PSNR)和均方差(MSE)。PSNR通常用来评价一幅图像处理后和原图像相比质量的标准。PSNR越高,处理后图像信息损失越小,公式如下:
经Matlab计算图像处理的信噪比也可以看出软阈值处理后的图像的信噪比15.13 dB大于硬阈值的13.53 dB。综上所述软阈值的去噪效果较硬阈值要好。
在软硬阈值实验结果的基础上,本文又对多级软阈值去噪的方法进行了仿真见图4。对加入信号不相关随机噪声的遥感图像先进行小波分解,再对高频系数进行多次软阈值处理。
从图5的PSNR和MSE结果可以看出,处理的次数越多,信噪比越高,但是对图像处理的次数越多对图像信号的损失也就越多,虽然带有高频信息的噪声得到有效的抑制但同时也导致图像越来越模糊。从图4与图5的去噪结果分析得出第2次的效果最佳。
4 结 语
本文介绍了遥感图像的噪声类型以及遥感去噪国内外发展状况。在传统数字图像去噪的基础上,介绍了基于小波变换的图像去噪理论。根据遥感图像中最常见的信号不相关随机的噪声,采用基于小波变换的阈值去噪方法,进而在硬软阈值去噪的基础上,进行软阈值的改进型算法,取得较好的实验结果。将小波应用于去除高光谱信号相关随机噪声将成为后续研究的主要方向之一。但由于小波理论较为复杂,并且是一种时频局部化分析方法,基于小波变换的遥感图像去噪中存在参数调节、小波基选取等问题,这些也将成为今后研究的内容。
参考文献
[1] 徐瑞.基于小波变换的遥感图像降噪与融合技术的研究[D].天津:天津大学,2008.
XU Rui. Study on denoising and fusion technology based on wavelet transform for remote sensing images [D]. Tianjin: Tianjin University, 2008.
[2] ZHOU X, TAN W, ZHANG L, et al. The research of remote sensing image denoising methods [J]. Industrial instrumentation & automation, 2015(3): 71?74.
[3] 胡小军,戴兵,秦飞.SPOT5遥感影像去噪与增强处理[J].江西测绘,2013,95(1):31?33.
HU Xiaojun, DAI Bing, QIN Fei. SPOT5 remote sensing image denoising and enhancement processing [J]. Jiangxi surveying and mapping, 2013, 95(1): 31?33.
[4] LIU X, BOURENNANE S, FOSSATI C. Reduction of signal?dependent noise from hyperspectral images for target detection [J]. IEEE transactions on geoscience & remote sensing, 2014, 52(9): 5396?5411.
[5] LIU X, BOURENNANE S, FOSSATI C. Denoising of hyperspectral images using the PARAFAC model and statistical performance analysis [J]. IEEE transactions on geoscience & remote sensing, 2012, 50(10): 3717?3724.
[6] 张乐飞,张良培,陶大程.张量分类算法的遥感影像目标探测[J].遥感学报,2010,14(3):519?533.
ZHANG Lefei, ZHANG Liangpei, TAO Dacheng. Tensor?based learning machine for remotely sensed image target detection [J]. Journal of remote sensing, 2010, 14(3): 519?533.
[7] 周世健,鲁铁定.双变量线性回归解算方法的等价性[J].江西科学,2009,27(6):867?870.
ZHOU Shijian, LU Tieding. The equivalence of the calculating methodology for bi?variable linear regression [J]. Jiangxi science, 2009, 27(6): 867?870.
[8] GOMEZ L, MUNTEANU C G, BUEMI M E, et al. Supervised constrained optimization of Bayesian nonlocal means filter with sigma preselection for despeckling SAR images [J]. IEEE transactions on geoscience & remote sensing, 2013, 51(8): 4563?4575.
[9] 吴知.基于小波变换的遥感图像去噪算法研究[D].南京:南京信息工程大学,2013.
WU Zhi. Remote sensing image denoising algorithm based on wavelet transform [D]. Nanjing: Nanjing University of Information Science & Technology, 2013.
[10] 刘晓莉,任丽秋,李伟,等.阈值优化的遥感影像小波去噪[J].遥感信息,2016,31(2):109?113.
LIU Xiaoli, REN Liqiu, LI Wei, et al. Threshold optimized wavelet for remotely sensed image denoising [J]. Remote sensing information, 2016, 31(2): 109?113.
[11] SARITHA M, KULKARNI S, HALAGATTI S. Image denoising using wavelets transform and adaptive least mean square method [C]// Proceedings of International Conference on Signal Processing, Communication, Power and Embedded System. Paralakhemundi: IEEE, 2017: 1961?1966.
[12] 邱毅.基于正交小波变换的信号降噪算法研究[J].电脑与电信,2008,1(6):67?68.
QIU Yi. Research on signals denoising algorithm based on orthogonal wavelet transform [J]. Computer & telecommunication, 2008, 1(6): 67?68.
[13] 张霞,孙伟超,帅通,等.基于小波变换的图像条带噪声去除方法[J].遥感技术与应用,2015,30(6):1168?1175.
ZHANG Xia, SUN Weichao, SHUAI Tong, et al. Image destriping method based on wavelet transform [J]. Remote sensing technology and application, 2015, 30(6): 1168?1175.
[14] 张静妙,高双喜,王晓娜.基于低秩字典学习的高光谱遥感图像去噪[J].控制工程,2016,23(6):823?827.
ZHANG Jingmiao, GAO Shuangxi, WANG Xiaona. Hyperspectral image denoising based on low rank dictionary learning [J]. Control engineering of China, 2016, 23(6): 823?827.

