用于胎压监测系统的一种改进贝叶斯估计数据融合的研究

安世奇,由东媛

(青岛科技大学自动化与电子工程学院,山东 青岛 266000)

汽车作为人们日常生活中的代步工具,行车的安全性引起人们的高度重视,而轮胎爆胎因其不可预测性和不可控性成为交通事故发生的主要原因。据相关资料统计,在中国高速上70%以上的交通事故是由于汽车轮胎爆胎引起的,而在美国则高达80%。轮胎爆胎主要与其压力和温度有关,汽车胎压监测系统作为一种能实时监测轮胎的压力和温度的系统,其稳定性、可靠性得到人们广泛关注。如何选择数据融合算法,有效减小系统的漏报和误报,得到精确的结果成为解决问题的关键[1-4]。

目前胎压监测系统大多都是采用单一传感器采集数据,但无法判断失效的数据以及故障的传感器,影响行车的安全性,多传感器信息融合技术充分利用多个传感器协同工作的优势,为提高可靠性和准确性提供了技术支持。文献[5]优化了基于贝叶斯估计的多传感器信息融合方法,采用均值的分批估计算法对多传感器数据进行融合计算,并应用于移动机器人局部定位中,结果表明此方法能有效解决多个传感器测量数据的不确定性和不一致性。文献[6]根据容许函数的阈值判别多个传感器的数据以得到有效数据,在分批估计得到最优估计值的基础上,依据权值最优分配原则进行自适应加权融合,进而提高系统的精确值。文献[7]提出一种基于异常数据驱动的簇内数据融合的方法,仅当数据异常时触发簇头节点,剔除不可靠数据后进行数据融合处理,该方法在保证有效数据不丢失的情况下,减少了节点间的数据通信量,提高了数据融合的准确性。本文基于贝叶斯估计的方法,采用模糊数学中隶属度函数,对多个传感器的数据进行判别,剔除失效的数据和故障的传感器,使用有效的数据计算融合值。然而,传感器采集的信号除了真实信号外还会引入噪声信号,结合卡尔曼滤波器消除噪声,以得到更为精确的融合结果。

1 胎压监测系统方案设计及工作原理

1.1 系统方案设计

胎压监测系统根据不同的分类方式,可分为三大类[8],如表1所示。

表1 胎压监测系统的分类

直接式TPMS通过轮胎模块中的传感器直接测量轮胎的参数(压力和温度)数据,间接式TPMS比较轮胎之间的转速差以达到监测胎压的目的,但是如果汽车有两个及以上轮胎的气压同时升高或降低,那么系统将无法正常工作。目前,无源式TPMS大多数还处于研究开发阶段,产品不成熟,外置式胎压监测系统的安全性低和抗干扰性差[9-10]。由于汽车胎压监测系统要求精度高、实时性强,鉴于以上分析,本文选择内置有源直接式TPMS进行研究。

1.2 TPMS工作原理

胎压监测系统中置于轮胎内部的多个传感器实时采集轮胎的压力和温度数据,通过无线射频技术进行信息传输。中央控制器将射频接收单元中的数据处理融合后,通过人机交互界面实时显示胎压和温度等相关信息,设置压力和温度报警阈值,当胎压或温度出现异常时给予司机报警提示,这种系统能够有效的预防由轮胎爆胎引发的交通事故,提高了行车的安全性。

由于安装在轮胎轮毂上的轮胎模块需锂电池供电,其使用寿命有限且安装过程复杂,所以为了降低模块的功耗,延长电池的工作寿命,本系统采用了低频唤醒技术,当无线终端需要工作时,低频唤醒模块主动唤醒各个轮胎监测发射处理单元中的微控制器,迅速进入工作状态[11]。图1为胎压监测系统原理框图。

图1 胎压监测系统原理框图

2 胎压监测信息融合模型

单一传感器测量不能全面分析轮胎内温度和压力情况,而基于贝叶斯估计的多传感器信息融合技术能够解决这一问题。首先对多传感器测量数据的可靠性进行估计,通过建立置信距离矩阵判断数据之间的关系,然后应用模糊数学中隶属度函数的概念剔除无效的数据,并根据贝叶斯估计融合剩余有效数据,最后,结合卡尔曼滤波器对融合数据优化以得到系统的最优估计。

2.1 多传感数据信号预处理

假设Xi和Xj分别表示第i和第j个传感器所测数据且均服从高斯分布,令xi和xj表示某一次测量中对应传感器的所测数据,则置信距离dij和dji分别为:

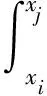
(1)

(2)

pi(x|xi)和pj(x|xj)分别为xi和xj的概率密度曲线,其中

(3)

σi为第i个传感器测量值的均方差,且σi=E{[x-E(x)]2}。dij和dji值反映了两个传感器之间的支持程度。

假设有n个传感器测量同一参数时,构建关于任意两个传感器所测数据的置信距离dij(i=1,2,…,n;j=1,2,…,n)的矩阵Dn。

(4)

确定置信距离矩阵后,引入模糊数学中的隶属度函数判别不同传感器之间是否相互支持,选择阈值γ1和γ2对置信距离dij进行划分,即

(5)

则可根据δij构建关系矩阵Rn,如式(6)所示:

(6)

根据δij的取值判断最佳融合数,当δij=1时,则说明第i和j个传感器相互支持,反之δij=0时,说明两个传感器之间不支持,并剔除只被少数传感器支持的传感器数据,如果此传感器的数据长期无效,需检查传感器是否存在故障。最佳融合数即为剔除无效数据后剩余有效数据的集合m。

2.2 基于贝叶斯估计的有效数据融合

车辆行驶过程中轮胎内部的压力和温度传感器由于其自身内部各个参数的变化以及所处的环境复杂多样,使得单一传感器测量的数据具有不确定性[12]。贝叶斯估计方法能够充分利用先验知识,适当处理采集的参数信息,补偿单一传感器测量轮胎的压力和温度的不确定性以及测量范围的局限性。

根据关系矩阵Rn可得m个有效数据分别为xi(i=1,2,…,m),被测参数W的Bayes(贝叶斯)估计值为:

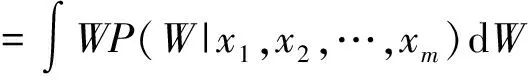
(7)

式中:条件概率密度函数P(W|x1,x2,,…,xm)未知,可由式(8)表示

(8)

(9)

由式(9)可知P(W|x1,x2,…,xm)也服从高斯分布,假设服从N(μN,σN),即

(10)

由式(9)、式(10)可得:

(11)

根据式(11)能够得出温度T和压力P的融合估计值。

2.3 优化的贝叶斯估计方法

胎压监测系统中传感器输出的信号主要由轮胎的压力和温度真实信号和噪声信号组成[13],由于胎压监测系统要求较高的精度,所以有必要对系统去噪。系统中的温度和压力传感器都属于线性动态系统,噪声的作用效果都接近于高斯白噪声[14],所以本文应用卡尔曼滤波器优化融合后的温度和压力估计值,提高系统监测的精度。设t时刻温度和压力状态值分别为T(t)、P(t)。

设线性离散系统:

(12)

式中:w(t)为过程噪声,v(t)为测量噪声;x(t)为状态向量,z(t)为观测向量;A(t)、C(t)为系数矩阵。

w(t)、v(t)的协方差矩阵分别为:

(13)

(14)

卡尔曼滤波算法分析如下:

(15)

卡尔曼滤波包括时间更新(预测)和测量更新(校正),时间更新将当前状态向量作为先验估计递推至测量更新,测量更新结合先验估计和新的测量变量以获得状态的后验估计,卡尔曼滤波联合观测信息及状态转移规律为融合数据提供最优估计[15]。

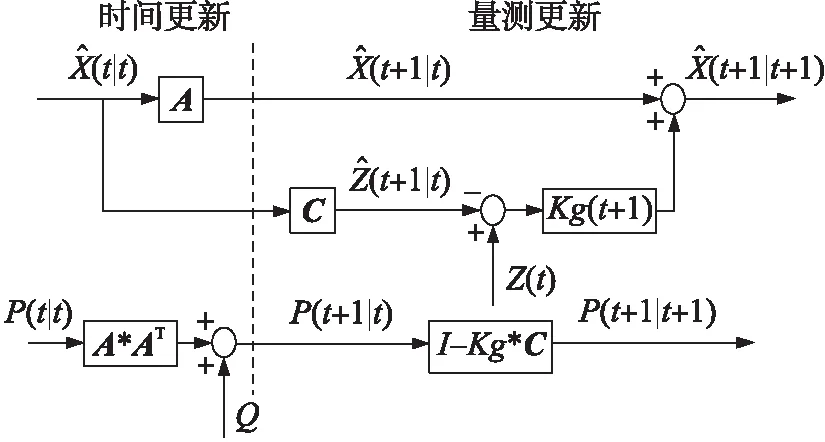
图2 卡尔曼滤波结构图

卡尔曼滤波算法公式中参数的选定:状态转移矩阵A取标量1即:A=[1];观测矩阵C=[1];过程噪声w和测量噪声v的协方差矩阵选定根据多次反复试验,调整滤波器系数确定最优值。

3 实验结果与仿真分析

3.1 实验数据采集及处理

针对小型汽车,每个轮胎内置3个SP370轮胎模块。行驶过程中,如果轮胎胎压高于基准胎压(基准胎压为200 kPa)1.2倍或低于基准胎压的50%时,胎压监测系统报警提示驾驶员停车检查轮胎情况,如无异常,适当降低车速,胎内温度高于75 ℃时(正常温度50 ℃～60 ℃)系统报警,高于85 ℃急速报警,危险系数极高。

本文以小型汽车左前轮压力数据为例,3个压力传感器对轮胎压力进行测量,每次测量5个数据,在保持相同的外界环境的条件下,某一时刻得到3个压力传感器数据如表2所示。

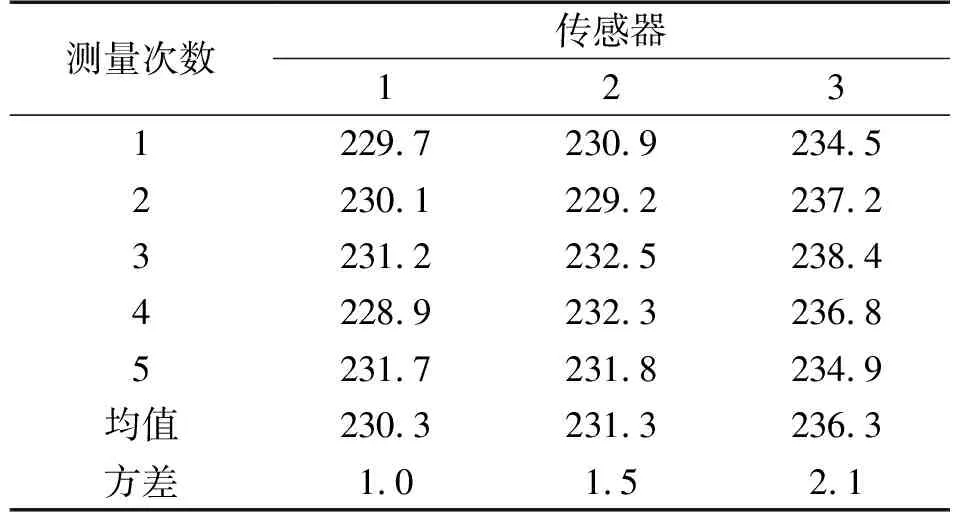
表2 轮胎压力测量数据

代入式(4)求得置信距离矩阵为:

根据隶属度函数确定阈值 和γ2=0.010 0,则关系矩阵为:

从关系矩阵能够看出压力传感器1、2融合性好(即m=2)。将3个压力传感器的数据融合后可得:

引入卡尔曼滤波器优化贝叶斯估计后轮胎压力值为:P=228.6 kPa。

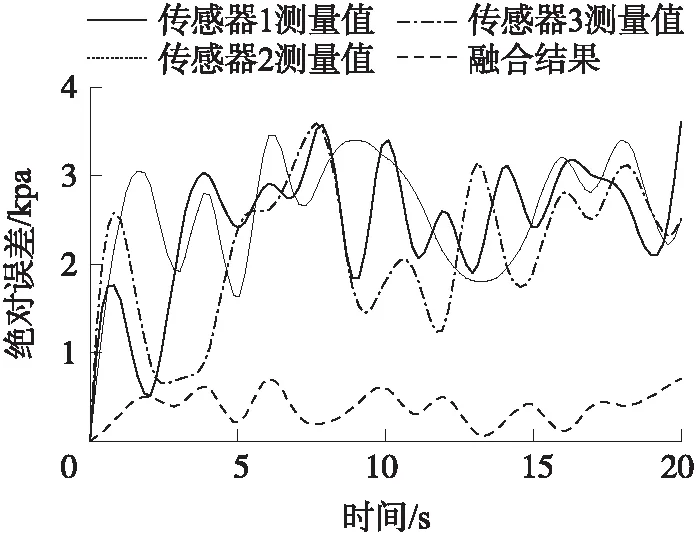
图3 传感器测量值及融合结果值与实际值的误差

3.2 仿真验证

传感器采集数据信号时由于自身特性以及受外界环境的干扰,使得测量结果产生误差,3个压力传感器测量误差值如图3所示。图3也表示了贝叶斯估计融合后所产生的误差。从图3中可以看出单一传感器的测量值与实际值误差较大,经过贝叶斯估计融合后的结果误差较小。因此,采用信息融合技术能够有效的解决单一传感器测量数据的不确定性和不一致性。

应用卡尔曼滤波器为了尽可能消除或减小噪声影响,提高实时监测数据的准确性。方差代表了数据与中心数据的偏离程度,方差越小,表明数据越接近真实值。从图4中能够看出,贝叶斯估计和卡尔曼滤波相结合后的方差值明显比贝叶斯估计后的方差值小,这也就证明了引入卡尔曼滤波器的有效性。

图4 融合后的方差及滤波后方差

4 结论

为了解决单一传感器测量数据的局限性,本文利用改进的贝叶斯估计的方法综合处理轮胎测量数据,通过对采集到的数据进行预处理,去除支持度较低的数据,采用贝叶斯估计的方法对数据进行融合,并改进融合方法以优化融合结果,得到监测数据的最优估计,从而提高整个系统的精度。实验证明,提出的方法能够有效的剔除失效的数据和故障的传感器,并能滤除噪声得到更为可靠的数据,从而避免了事故的发生。

参考文献:

[1] 梁涛,杨伟达,杨玉坤,等. 轮胎压力监测及控制系统[J]. 传感技术学报,2016,26(4):627-632.

[2] 赵新,徐克宝. 基于SP37的汽车胎压监测系统研究与设计[J]. 电子测量技术,2015,38(10):87-95.

[3] 张鉴,戚昊琛,杨文华,等. 一种用于胎压监测的MEMS压力传感器设计[J]. 电子测量与仪器学报,2015,29(10):1424-1430.

[4] 张昊.无线无源轮胎压力和温度传感器及监测系统研究[D]. 广西:广西工学院,2012.

[5] 张品,董为浩,高大冬. 一种优化的贝叶斯估计多传感器数据融合方法[J]. 传感技术学报,2014,27(5):644-647.

[6] 王华东,王大羽. 一种改进的多无线传感器数据分批估计自适应加权融合算法[J]. 传感技术学报,2015,28(8):1239-1243.

[7] 谭德坤,付雪峰,赵嘉,等. 基于异常数据驱动的WSN簇内数据融合方法[J]. 传感技术学报,2017,30(2):306-312.

[8] 秦秀常.胎压监测系统(TPMS)的研究与设计[D]. 四川:电子科技大学,2014.

[9] 周玉兰. 基于多传感器融合的轮胎压力监测系统研究[D]. 西安市:西北工业大学,2005.

[10] 王进. 汽车轮胎压力与温度监测预警系统的研究[D]. 湖南:中南大学,2009.

[11] 潘粟城. 车载蓝牙胎压监测技术研究[D]. 上海:华东理工大学,2016.

[12] Antriksh Sharma,Nishant Pandharpurkar. The Effect of Wheel of Spin Velocity on the Propagation of Signal to Enhance the Performance of Tire Pressure Monitoring System. Industrial Instrumentation and Control(ICIC),India,2015.

[13] 李丽宏. 基于多传感器信息融合的超限超载检测系统设计研究[D]. 山西:太原理工大学,2013.

[14] 刘涛,张文平,陈慧芳,等. 卡尔曼滤波在分布式拉曼光纤温度传感系统去噪中的应用[J]. 红外与激光工程,2014,43(5):1643-1647.

[15] Janjic Tijana,Nerger Lars,AIbertella AIberta,el al. On Domain Localization in Ensemble-Based Kalman Filter Algorithms[J]. Monthly Weather Review,2011,139(7):2046-2060.