经典灰色理论和马尔科夫链的交通量预测模型构建

南爱强, 王锋宪

(1.云南交通职业技术学院,昆明 650500;2.昆明理工大学 建工学院,昆明 650500)

0 引言

短时交通流量整体预测相较长期的交通量预测具备了更高的不确定性，并且在随机预测过程中会受到多方面的因素影响，整体的交通量预测规律也较不明显。迄今为止，已经出现了较多短时期的交通量预测模型方法，主要包括了[1]：1)基于线性理论的模型构建，比如使用“卡尔曼滤波法”等；2)基于计算机终端设备的智能化预测模型，比如使用“非参数回归法”以及“神经网络法”；3)基于非线性理论模型构建方法，比如使用“小滤波分析法”；4)基于数据组合的预测方法，比如使用多种方法以及两种方法的整体综合；5)基于交通模拟预测方法，比如“动态交通分配”等。灰色系统理论被较为广泛的应用于近些年来的多方面预测，比如对于城市噪声、灰色预测以及自然灾害等多方面的灰色预测方面。在近些年来的发展中，对于交通领域的相关研发人员，通过应用灰色理论概念在城市交通量的预测以及道路交通量，还有铁路货运量和公路客运量等多方面的预测。由此本文构建基于经典灰色理论和马尔科夫链的交通量预测模型展开研究。

1 灰色理论马尔科夫预测模型构建原理简述

灰色理论马尔科夫预测模型，在构建系统性的短期数据预测过程中，具备了较高的精准度、较快的收敛速率以及存在整体的较广使用范围，适用于灰色系统的数据预测方面。基于经典灰色理论的交通量预测模型构建，有效的突破了传统的预测模型应用需要海量历史数据这一弊端，不需要对预测结果造成影响的相关因素加以罗列[2]。在具体的应用过程中主要经由时间序列寻找相对应的规律性信息，发现其中所存在的主要规律，构建交通量预测模型。但是此种模型的构建，需要借助指数曲线完成数据的拟合。所完成的相应拟合数据序列，主要所呈现的相应曲线通常是光滑的。由此这一模型通常会存在较大的预测数值波动性，因而致使交通量的预测失真。对于这一情况的解决，通过将马尔科夫链理论引入其中，来有效的解决这一弊端问题。借助经典灰色理论融合马尔科夫链，构建新型的交通量预测模型[3]，从而利用灰色预测对交通事故的整体发生趋势进行预测，还可经由马尔科夫链对具体的交通状态变化规律得以显示，有效的提升了整体的交通量预测精准度。

2 构建灰色理论和马尔科夫链交通量预测模型

通过基于灰色理论和马尔科夫链完成交通量预测模型的构建，具体的构建模型如下：通过先基于经典灰色理论，对原本的交通量数据X(0)完成预测模型构建，在此基础之上完成灰色理论模型的构建，之后将模型结合马尔科夫链理论，完成残缺差值符号的构建以及状态转移概率矩阵。

2.1 构建原始数据的灰色理论预测模型

通过依照经典灰色理论，将原本的数据序列X(0)={x(0)(1)，x(0)(2),…x(0)(n)}，从而对未来短时期阶段内的交通量变化趋势进行预测，在原本的数据累积基础之上，增强了整体的数据预测规律性，针对一次性累积完成了数据序列的生成X(1)={x(1)(1),x(1)(2),…,x(1)(n)}。

(1)

在该公式中，a与u主要代表未辨别的预测量参数。由该方程式的解析解得出式(2)。

(2)

在该解析式(2)中的X(0)(1)=X(1)(1)为预测的初始数值。之后借助最小二乘法来完成对未辨别预测量参数a和u的计算，如式(3)。

(3)

在该公式中的Y和B主要如式(4)和式(5)。

Y=(x(0)(2),x(0)(3),…,x(0)(n))T

(4)

(5)

通过依照上述的基于灰色理论预测模型，从而求解得出一次性的累计生成数量x(1)(t)的模型预测数值，经由公式转换得出了原始数据的模型数值如式(6)。

X(0)(t)=X(1)(t)-X(1)(t-1)。

(6)

2.2 马尔科夫链划分及状态转移矩阵计算

1)马尔科夫链的状态划分

通过将具体的预测数值设置为x(0)(k)，之后完成数值差的拟合e(k)，通过借助这一数值差拟合有效的实现了划分系统状态。

2)状态转移矩阵

进行纳税的双方都有责任履行义务。现阶段，应该加强增值税的立法，将其上升为法律，在一定程度上强调税法的刚性，进而实现市场经济秩序的稳定。

通过设置Aij(n)设置相应的状态θi，经由几个步骤完成了θj的样本均数值的转移，ψi作为原本的θi状态的样本数值，那么pij(n)=Aij(n)/ψi，就会由原本的θi状态的样本数值，转换为θi的n个转换步骤概率。N步的转换概率具体表现,为式(7)。

(7)

3)预测数值的计算

通过完成如上的状态性转移矩阵的确定之后，完成相应的系统所处状态分析，之后经由概率加权获取了系统性的特征数值预测,得出式(8)。

(8)

3 灰色马尔科夫预测模型

在任何的灰色理论预测模型应用中，随着时间段的逐渐推移，就会不断的发生多种无从预测以及随机性的驱动因素，从而导致灰色马尔科夫预测模型预算系统受到了较多的影响，准确度不仅仅较高原点的数据之后1-2个数据，如图1所示。

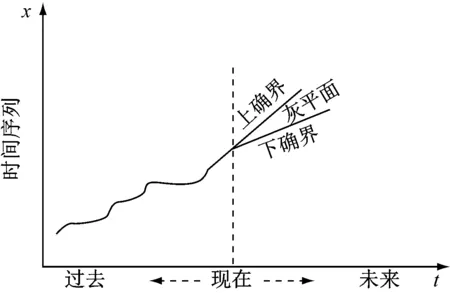
图1 GM(1,1)预测精度受时间推移影响

时间越长，越呈现上升的发展趋势，就会对原本的时间点原理产生偏离，从而致使整体的模型预测准确度逐渐降低。

由此在具体的应用过程中，就需要针对那些具体的影响因素展开考虑，如何能够解决随着时间的逐渐推移从而导致系统模型的整体预测精准度受到影响，以此来有效的减小历史变化数据，构建相对应的等级递推类的经典灰色理论和马尔科夫链的交通量预测模型。在使用该模型完成相应的预测过程中，只有不断的完成将最旧的数据进行排除，不断融入新型的预测数据，以此有效保持数列的等维度，只有这样逐步的完成才能最大限度的确保预测目标的整体精准度。基于经典灰色理论和马尔科夫链的交通量预测模型主要的构建步骤包括如下：

1)通过针对原始模型中所产生的流量数据完成处理，其中主要包括了旧数据以及无效和较为特殊奇怪的数据，之后构建等间隔时间段的序列性交通量数据；2)对处理后的数据构建灰色预测模型，之后经由上述文中所提公式完成序列X(0)(k)的计算；3)利用数据的波动性处理方法，有效的将原本的预测值进行还原；4)计算GM(1,1)的残差数列数值；5)利用上述文中所分析得出的e(k)、X(0)(k)，对马尔科夫状态完成划分，进一步完成对状态的矩阵转移展开计算；6)对X(0)(k)的马尔科夫修正数值进行计算预测，从而得出争取的交通量预测数值f；7)对数据列完成进一步的更新，之后容纳新的数据信息，排除旧的数据信息，从而构建了新型的等同维度的递推类预测模型；8)返回第二个步骤，持续重复第二步至第七步，完成对下一个时间阶段的序列数值确定。

4 基于经典灰色理论和马尔科夫链的交通量预测模型仿真应用实例

传统的模型预测，主要预测数值序列是平滑的预测曲线，曲线的变动趋向可以将具体检测流量变化趋势得以反应。本次研究实例基于构建GM(1,1)为第一点解微分方程舒适条件，曲线过第一点之后，符合最小二乘法，在过第二点时会发生突变，由于阶段性长时间序列，完成逐步预测，提升整体模拟进度的预测模型。选自某地区一桥断面为例，对该地区的交通量相关数据展开实地调查，由早上7点至9点30分，每隔15分钟完成一个交通量的调查，主要测量所得的具体数据,如表1所示。

表1 交通量时间段统计表

通过选取该表中的前8段时间段作为原始数据，之后取9、10两个时间段作为预测数据，通过让X(0)(t)={504,559,631,638,703,623,862,677,935，686}，构造相应的矩阵数值B以及向量数值Y，经由公式(5)可以通过最小二乘法求出最终的数值为公式(9)：

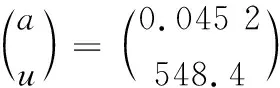
(9)

最终得出所累积的预测数列模型：X(1)(t+1)=130 22e0.045it-12 517

进而得出原始的数据模型数值：X(0)(t+1)=(1-e0.045it)13 0220.045it

之后通过对上述数值模型的计算可以得出模型值以及残差，如表2所示。

表2 模型数值及残差数值

通过对上表所得的残差数值，构建GM(1,1)的预测模型，得出相应的残差绝对值预测模型数字，完成如上的建模可以得出最终的修正后模型，那么该模型所主要得出的结果，如表3所示。

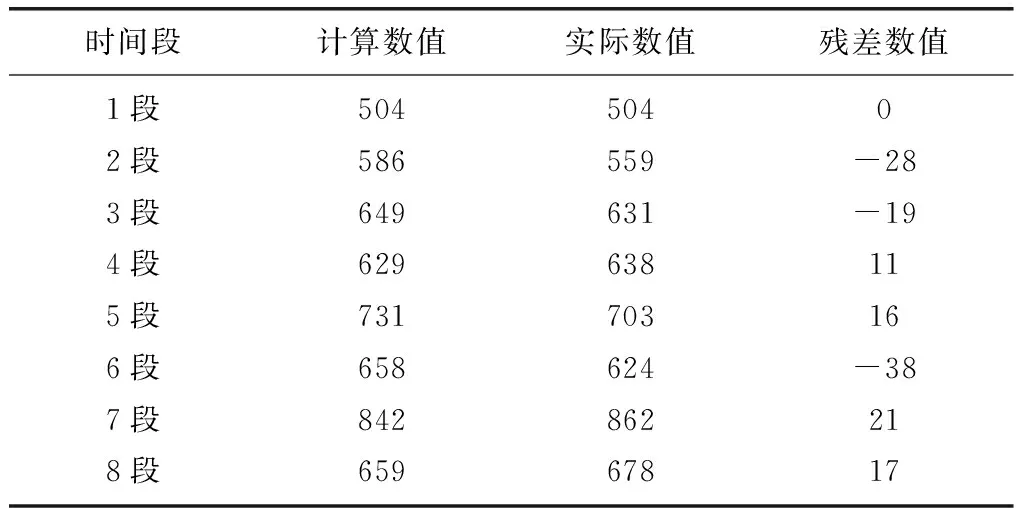
表3 模型值以及残差数值

通过依照上述的预测模型预测数间段9段、10段交通量，具体的结果，如表4、表5所示。

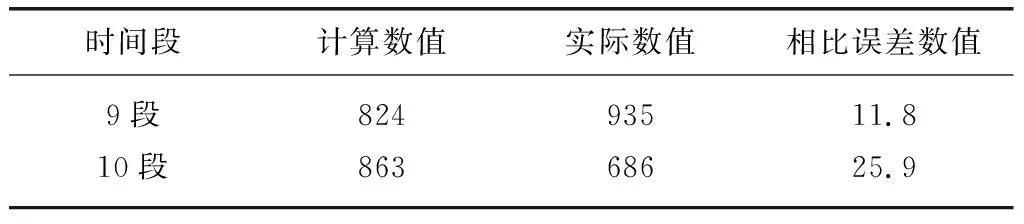
表4 灰色理论GM(1,1,)结果

表5 灰色马尔科夫链模型结果

可以经由数据发现灰色马尔科夫链对于模型的交通量整体预测具备了较高的精准度，并且能够最大限度的减少预测误差数值。

5 总结

通过如上基于经典灰色理论和马尔科夫链，针对灰色马尔科夫链预测模型构建，发现通过基于原始数据的序列及残差绝对数值，完成GM(1,1)的预测模型构建，之后在其中引入马尔科夫链的具体状态转移概率矩阵，构建了灰色马尔科夫链预测模型。后应用于实例发现灰色马尔科夫链对于模型的交通量整体预测具备了较高的精准度，并且能够最大限度的减少预测误差数值。