基于Abaqus的有限元薄壁结构静强度分析方法研究

(中国飞机强度研究所，陕西 西安 710065)

0 引言

薄壁结构主要由薄板、薄壳和细长杆等组成，能以较少的材料承受较大的载荷，在飞行器设计等方面有较大应用。随着计算机技术的发展，薄壁结构的工程强度校核分析常采用有限元分析方法。为了追求计算速度，设计人员在方案设计时多采用有限元软件的自由网格划分技术，网格单元的尺寸多设为薄壁的壁厚；有时为了降低计算模型网格的数量，提高计算速度，有限元网格尺寸甚至大于薄壁的厚度。此种网格划分方式虽然计算速度较快，但因网格尺寸相对薄壁厚度较大，会产生单元刚化现象，从而导致结果出现较大误差，影响方案设计[1]。本文对在进行薄壁结构强度计算时经常采用的六面体单元、四面体单元和壳单元等网格类型进行研究，探究这三种类型的网格和不同网格尺寸对薄壁结构的强度、刚度的计算结果准确性的影响。

1 结构静强度有限元分析流程

有限元分析法是通过单元结点上的位移量为直接求解未知量，为了能用单元的结点位移表示单元的应力和应变分离，有限元分析法假定了一个位移模式，也就是单元上的位移插值函数[2]。结构静强度有限元分析与评估规范流程见图1。

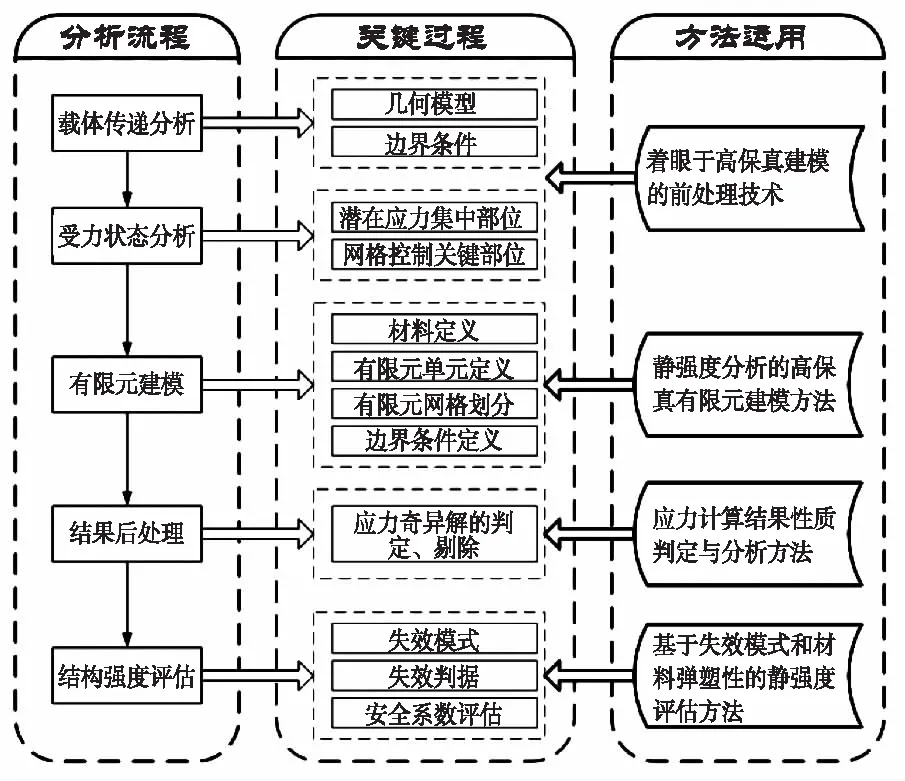
图1 结构静强度有限元分析规范流程图

2 有限元建模及网格划分

2.1 试验件的尺寸及属性

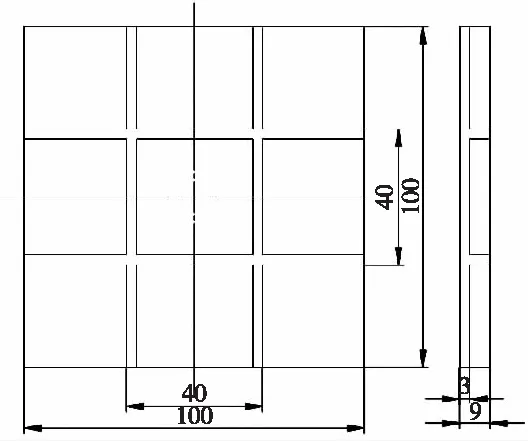
图2 薄壁平板试验件结构尺寸图

现选取典型薄壁结构：单侧有井条形筋板的平板作为研究对象，对其进行有限元建模分析。平板及筋板厚度均为3 mm，结构尺寸如图2。试验件为通用钢材Q345，重量为0.29 kg，密度为7.85 g/mm3，弹性模量为206 GPa，泊松比为0.3。

2.2 有限元模型的载荷和边界

图3 试验件的载荷及边界

试验件在无筋板一侧承受1 MPa的面压，边界条件为矩形平板四边位移约束，载荷及边界条件见图3。

2.3 有限元模型的网格分析

有限元网格生成是有限元计算的关键环节，生成的网格应满足以下要求[3-4]：

1)单元之间不能相互重叠；

2)单元要与原物体的占有空间相容，即单元既不能落在原区域之外，也不能在原区域边界内出现空洞；

3)单元的形状应合理，每个单元尽量趋近于正多边形或正多面体，不能出现面积很小的二维尖角元或体积很小的三维薄元；

4)网格的密度应分布合理，分析值变化梯度大的区域需要细化网格；

5)相临单元的边界相容，即不能从一个单元的边或面的内部产生另一单元的顶点。

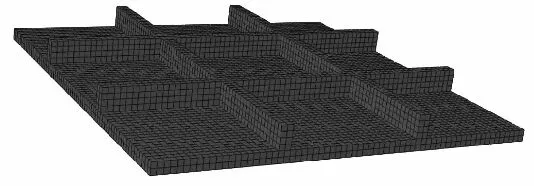
图4 网格尺寸为1.5 mm的六面体单元

对试验件分别建立六面体单元、四面体单元和壳单元的网格划分，网格尺寸分别为3 mm、1.5 mm、1 mm、0.75 mm和0.6 mm，此时板厚方向上的网格数量分别为1、2、3、4和5。现以1.5 mm的网格单元为例，六面体单元、四面体单元和壳单元的网格分布示意图分别如图4-图6。

图5 网格尺寸为1.5 mm的四面体单元 图6 网格尺寸为1.5 mm的壳单元

3 有限元计算及结果分析

为研究不同网格类型对薄壁结构的刚强度的影响，现分别对试验件同一网格尺寸的不同网格类型的模型进行有限元计算。为研究网格尺寸对薄壁结构的刚强度的影响，对不同单元类型的有限元模型分别进行不同网格尺寸的有限元计算。

3.1 六面体单元模型的计算

现分别对网格尺寸为3 mm、1.5 mm、1 mm、0.75 mm和0.6 mm六面体单元的试验件模型进行有限元计算。当网格尺寸为1 mm时，试验件的应力云图和应变云图分别如图7和图8。

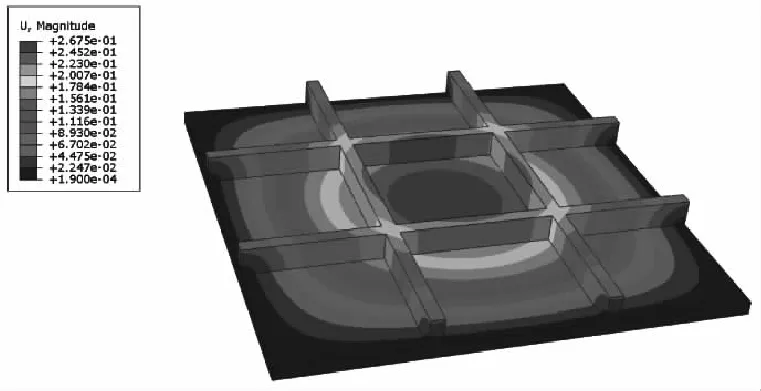
图7 网格尺寸为1 mm时的应力云图

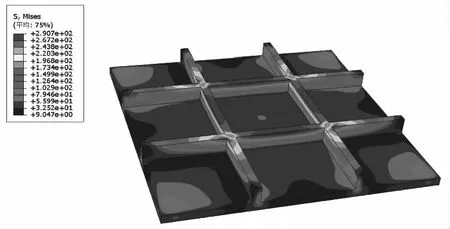
图8 网格尺寸为1 mm时的应变云图

当网格为六面体单元时，随着网格的不断细化，试验件的最大应力和最大变形量的变化如表1。

表1当网格为六面体单元时的应力、应变汇总表

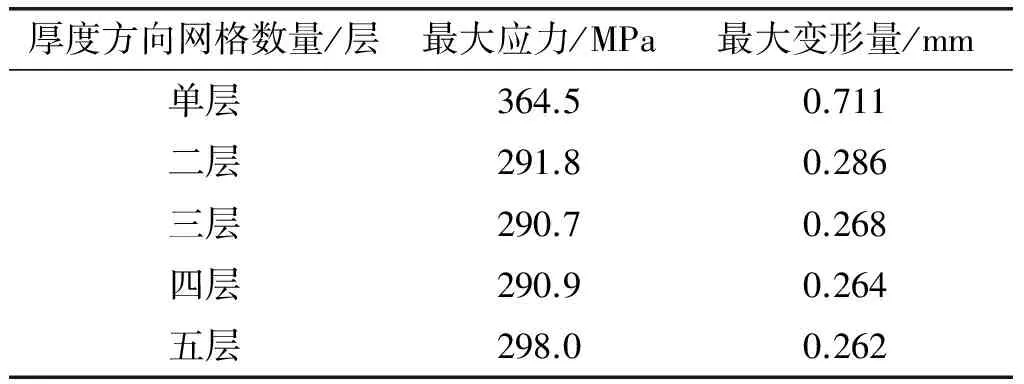
厚度方向网格数量/层最大应力/MPa最大变形量/mm单层364．50．711二层291．80．286三层290．70．268四层290．90．264五层298．00．262

利用表1生成六面体单元的应力、应变随网格尺寸的变化趋势图见图9。

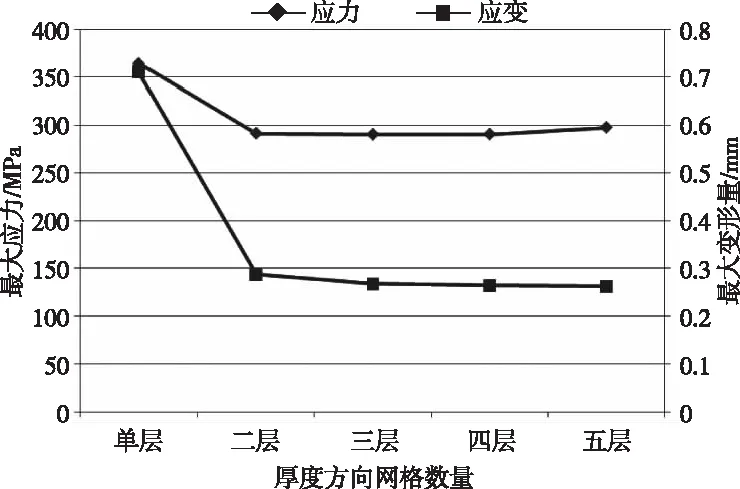
图9 应力及应变随网格尺寸的变化图

由图9可知，在利用六面体单元计算薄壁结构的应力和应变时，不同尺寸的网格单元对计算结果有较大影响。当板厚方向为单层网格时，计算结果不准确：应力值误差为25.6%，应变值误差为168.3%；当板厚方向上的网格数量大于等于2时，计算结果较准确。所以在利用六面体单元进行薄壁结构的刚强度计算时，板厚方向上至少需要2层网格。

3.2 四面体单元模型的计算

现分别对网格尺寸为3 mm、1.5 mm、1 mm、0.75 mm和0.6 mm四面体单元的试验件模型进行有限元计算。当网格尺寸为1 mm时，试验件的应力云图和应变云图分别如图10和图11。

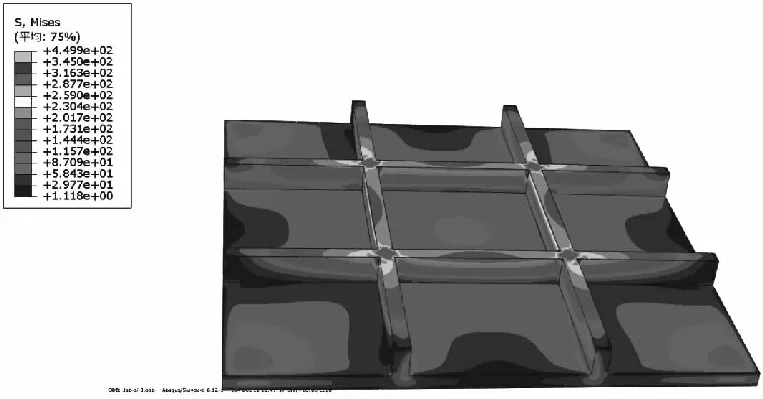
图10 网格尺寸为1 mm时的应力云图

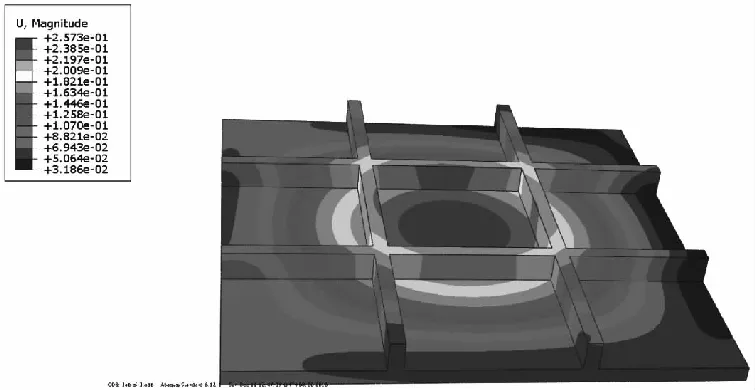
图11 网格尺寸为1 mm时的应变云图

当网格为四面体单元时，随着网格的不断细化，试验件的最大应力和最大变形量的变化如表2所示。

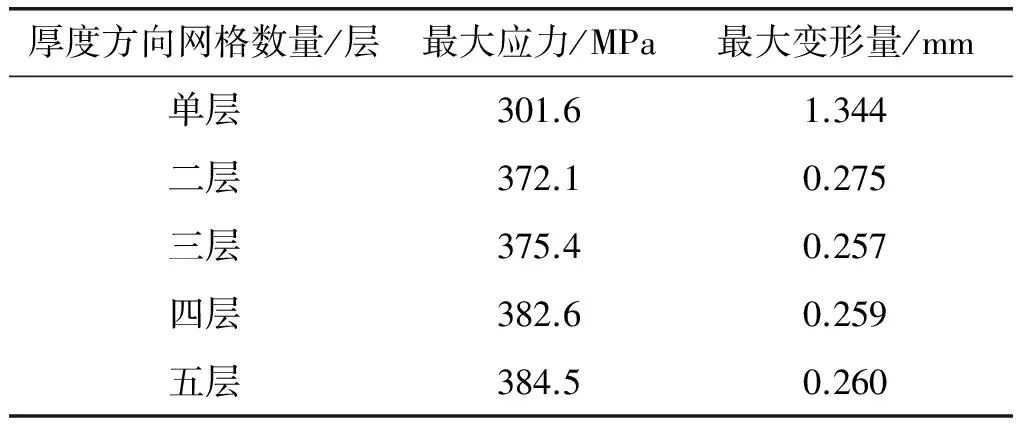
表2 当网格为壳单元时的应力、应变汇总表

利用表2生成四面体单元的应力、应变随网格尺寸的变化趋势图见图12。

由图12可知，在利用四面体单元计算薄壁结构的刚度时，单层网格存在着应变明显增大的情况，当板厚方向网格数量大于等于2时，强度和刚度计算结果较准确。

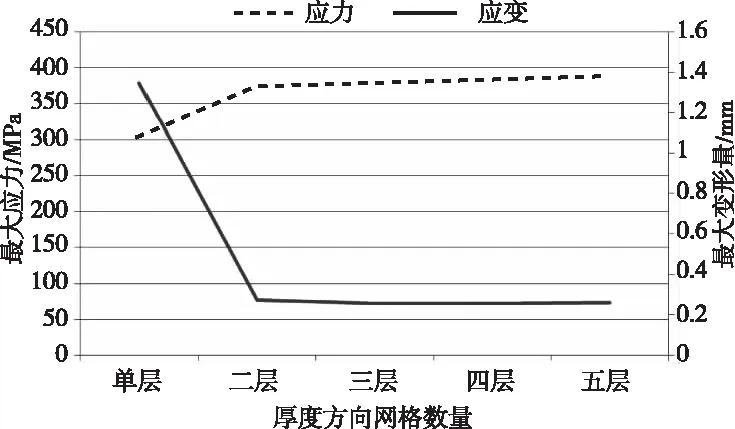
图12 应力及应变随网格尺寸的变化图

3.3 壳单元单元模型的计算

现分别对网格尺寸为3 mm、1.5 mm、1 mm、0.75 mm和0.6 mm壳单元的试验件模型进行有限元计算。当网格尺寸为1 mm时，试验件的应力云图和应变云图分别如图13和图14。

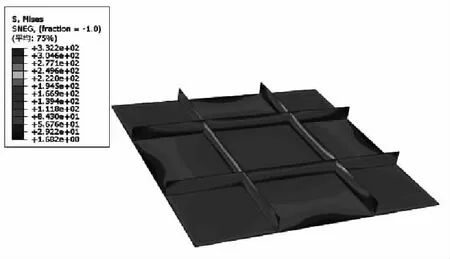
图13 网格尺寸为1 mm时的应力云图

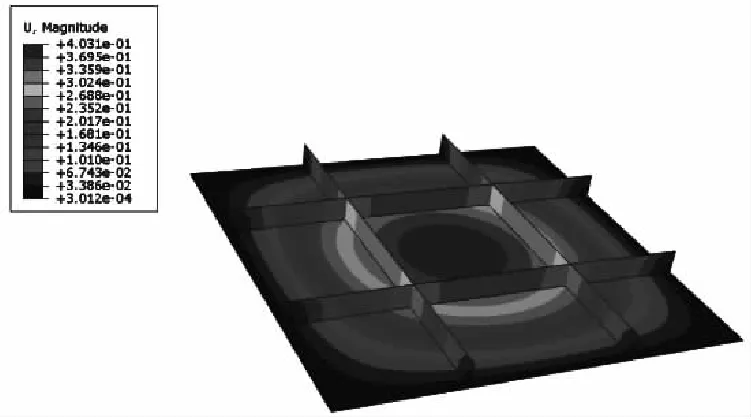
图14 网格尺寸为1 mm时的应变云图

当网格为壳单元时，随着网格的不断细化，试验件的最大应力和最大变形量的变化如表3。

利用表3生成壳单元的应力、应变随网格尺寸的变化趋势图见图15。

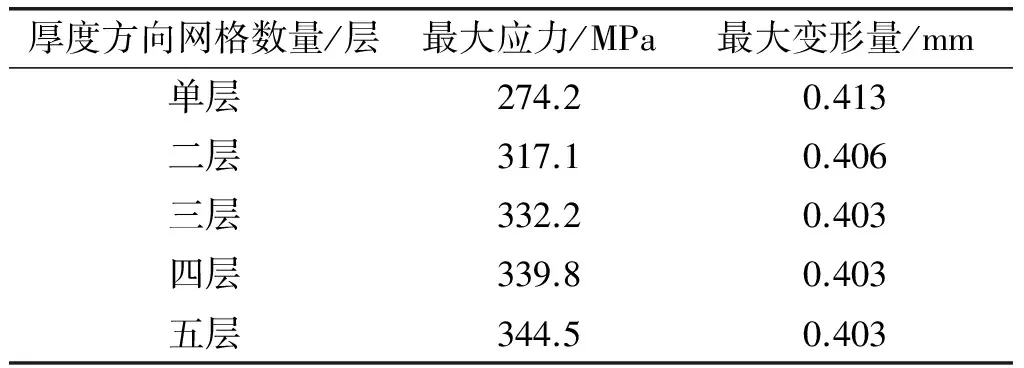
表3 当网格为壳单元时的应力、应变汇总表

由图15可知，在利用壳单元计算薄壁结构的刚强度时，单层网格存在着应力明显偏小的情况。所以在利用壳单元进行薄壁结构的刚度计算时，当结构件的尺寸较大时，可以采用单层网格；在利用壳单元进行薄壁结构的强度计算时，板厚方向上至少需要两层网格，且随着网格密度的增大，结构件的应力呈现出明显上升的趋势。

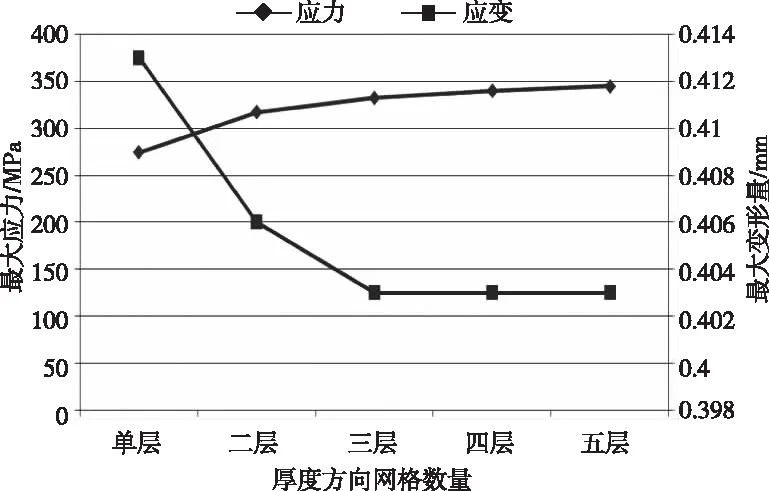
图15 应力及应变随网格尺寸的变化图

4 结果分析

对于复杂应力状态下结构网格选择，为了保证足够的计算精度，应优先选择带有中间节点的六面体单元或四边形单元，以降低计算精度对网格密度的依赖，节约计算资源，提高计算效率。对于几何复杂部位，可以选取壳单元，并进行网格加密，以尽量减小计算精度损失[5-6]。

网格划分过程中应采用有差别的网格尺度控制方法，具体为：

a)关键部位网格尺度较小，非关键部位(如辅助几何体)网格尺度较大；

b)应力集中区网格尺度较小，非集中区网格尺度较大，为保证圆角等应力集中部位的计算结果收敛性，其对应的网格尺度应确保单段弧长不少于3个单元；

c)对于网格尺度梯度较大的有限元模型，应采用阶梯式网格过渡，否则网格尺度梯度较大的界面容易产生结果失真；

d)网格尺度过渡时，优先选择采用形状不规则的单元，以兼顾计算精度和建模工作量，对于大型有限元模型，采用节点约束方程的方式实现网格尺度过渡工作量巨大，不便应用。