Improvement of an ID-Based Deniable Authentication Protocol
Tzu-Chun Lin
Abstract—The deniable authentication protocol is an important notion that allows a receiver to identify the source of a given message, but not to prove the identity of the sender to a third party. Such property is very useful for providing secure negotiation over the Internet.The ID-based deniable authentication protocol based on elliptic Diffie-Hellman key agreement protocol cannot defend the sender spoofing attack and message modification attack. In this paper, we present an improved protocol based on double elliptic Diffie-Hellman scheme. According to the comparison result,the proposed protocol performs better.
1. Introduction
The concept of deniable authentication protocol was initially introduced by C. Dworket al.[1]. The traditional authentication protocol assures the identification of communicated parties. One of drawback is the privacy issue. In compared with the traditional authentication, the deniable authentication has two special characteristics:
It enables an intended receiver to identify the source of a given message.
The intended receiver cannot prove the identity of the sender to any third party, even if he/she fully cooperates with the third party.
Due to the above two characteristics, the deniable authentication protocol can be broadly used for online shopping, electronic voting system, e-learning system,negotiation over Internet, etc. In 1998, C. Dworket al.[1]introduced the notion of interactive deniable authentication protocol based on concurrent zero-knowledge proof. At the time, Y. Aumann and M. Rabin[2]proposed an interactive deniable authentication protocol based on the factoring problem. However, both protocols have a common weakness,they are vulnerable to the person-in-the-middle attack. This means that a third party can impersonate the intended receiver to identify the source of a given message. In 2004, Z. Shao[3]proposed a first non-interactive deniable authentication scheme based on the ElGamal signature scheme. In general, noninteractive protocols are more effective than interactive protocols because of less communication cost. As a result,many non-interactive deniable authentication protocols have been designed. Their security is based on different mathematical hard problems. However, most of these schemes have some drawbacks. For example, in 2005, R. Lu and Z. Cao proposed two non-interactive deniable authentication protocols based on bilinear pairing and integer factorization problem,respectively. These two protocols still fail to achieve the second feature of the deniable authentication scheme[4],[5]. In 2006, W.-B. Leeet al.[6]proposed a deniable authentication protocol based on the generalized ElGamal scheme. They claimed that its communication process is shorter than Z. Shao’s protocol. But Y. Zhang[7]pointed out that W.-B. Lee’s protocol requires more transmission bits than Z. Shao’s protocol. In 2011, C.-Y. Liuet al.[8]showed that Z. Shao’s protocol fails to achieve the second requirement of the deniable authentication scheme. In 2013, J. Kar proposed an ID-based deniable authentication protocol based on elliptic Diffie-Hellman key agreement protocol[9]. However, in 2015,E.-J. Yoon[10]pointed out that Kar’s protocol cannot defend so-called sender spoofing attack and message modification attack. In this note, we present an improved protocol which defends such attacks.
The remainder of this paper is organized as follows. In Section 2, we briefly present some required mathematical properties. In Section3 we review Kar’s ID-based deniable authentication protocol. Our protocol with the security analysis and the performance analysis are presented in Sections 4 to 6. And Section 7 draws the conclusions.
2. Preliminaries
In this section, we briefly outline some basic knowledge which is used in the paper.
2.1 Elliptic Curves and Pairing
Definition 1. An elliptic curve over a finite fieldFpis roughly defined to be an equation of the Weierstraß form
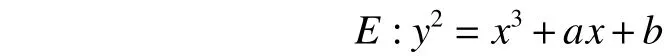
witha,b∈Fpsatisfying.
Let ∞ denote the point at infinity and letqbe a power of the primep. The setE(Fq) of rational points on an elliptic curveEoverFq
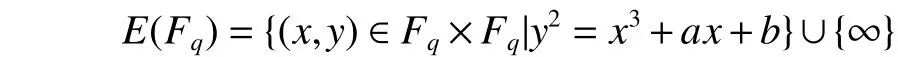
under the addition is an Abelian group.
Definition 2. LetGbe an additively-written group and letGTbe a multiplicatively-written group of the same order. A mappingis called a bilinear pairing, if it satisfies the following conditions:
1) Bilinearity: For allP,Q,R∈G, we have
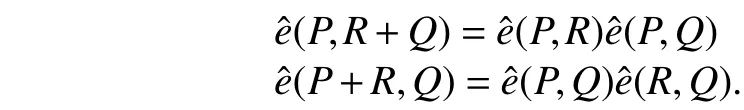
Note that if a bilinear pairing is used on elliptic curves, then usually the Weil pairing or Tate pairing is to recommend. For more information about elliptic curves and bilinear pairing,please see [1], [11] to [13].
2.2 Security Problems
The security of the protocols described in the paper is dependent on the intractability of the following problems. LetGbe an elliptic curve over a finite field of the ordern.
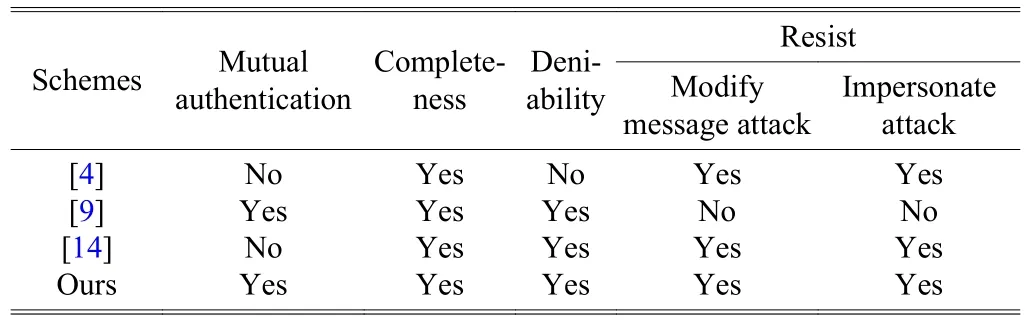
Definition 3. (Elliptic curve discrete logarithm problem(ECDLP)) GivenQ,R∈G, find an integer 0 Definition 4. (Decisional Diffie-Hellman problem (DDHP))GivenP,aP,bP,cPinGandk, determine whethermodn. Definition 5. (Hash decisional Diffie-Hellman problem(HDDHP)) LetHbe a secure cryptographic Hash function.GivenP,aP,bP∈Gandk, determine whether. Definition 6. (Computational Diffie-Hellman problem(CDHP)) GivenP,aP,bP,cPinG, computeabP. We review the Kar’s ID-based deniable authentication protocol. Suppose that Alice (as a sender) wants to send a messagemto Bob (as a receiver). In the beginning, some parameters are selected: A large finite fieldFq, an elliptic curveEoverFqin order to construct an additive Abelian subgroupG1ofE(Fq), and a base pointP∈G1of large order. Letbe two cryptographic Hash functions. Moreover, IDsand IDrdenote Alice’s and Bob’s identification, respectively. The Kar’s ID-based deniable authentication protocol is described as follows. Key Generation Alice chooses an integertsand sets the valueasand the pointQs Similarly, Bob chooses an integertrand sets the valuearand the pointQr. In order to encrypt the information, Bob needs to add an encryption key denoted asand the corresponding decryption key. Bob’s private key isand the public key is. Send Phase 1) Alice concatenatesQswith the timestampTand encrypts it by using Bob’s public key: 4) Alice computes wheremis the deniable message. Alice sends the deniable authentication informationto Bob. Receive Phase 1) Bob recovers the messagemby computing The security of Kar’s protocol is based on DDHP and HDDHP. It is a non-interactive protocol and can be easily implemented in mobile devices, such as the pad and smart card. The major computational cost for the performance of the protocol amounts to one encryption (decryption), onepoint multiplication and three Hash evaluations by both of the sender and receiver. However, E.-J. Yoon[10]has discovered two weaknesses of Kar’s protocol. Following,we explain why Kar’s protocol cannot resist these two attacks. Suppose that an attacker, named Eve, can intercept the pair. Then Eve performs the following steps: 1) Eve selects a random integeraeand computes 3) Letmebe a fake message of Eve. After receiving,Eve computes the session key: Bob verifies the validity of the equalityand the time stampTe. Because, Bob will believe the trustworthy of the attacker Eve. Suppose that Eve can interceptand the deniable messagem. Then 1) Eve extracts the Hashed valueby computing 2) Eve computes a modified whereTeis the current timestamp of Eve. 3) Eve sends the fake authenticated informationto Bob. 6) Bob verifies the validity of the equalityand the timestampTe. Because, Bob will believe the trustworthy of the attacker Eve. In this section, we present a mutual deniable authentication scheme based on the double Diffie-Hellman key agreement and pairing. Choose a cyclic subgroupG1ofE(Fq) and two generatorsPandRof the ordernand a bilinear pairing,whereGTis a multiplicative group of the ordern. Letandbe two cryptographic Hash functions. Moreover, IDsand IDrdenote Alice’s and Bob’s identification, respectively. Key Generation Alice chooses an integerts Send Phase 1) Alice encrypts her private keyQsby using Bob’s public key: If it holds, Alice acceptsQr; otherwise rejects. If, then Alice performs the following step.4) Alice computes Then, Alice sends the deniable authenticated informationto Bob. Receive Phase 1) Bob computes The major computational cost for the performance of the protocol amounts to one encryption (decryption), two-point multiplications, one Hash evaluation, and one pairing evaluation by both of the sender and receiver. In the following, we demonstrate that our protocol not only guarantees the deniability, but also resists the sender spoofing and the message modification attacks. Proposition 1. The sender Alice can identify the receiver Bob. Proof. Suppose that Eve impersonates Bob to communicate with Alice. Eve has to send the Hashed value(see the step 2)of the send phase) to Alice. Also, Eve has to create the session key. To this end, Eve has to decrypt the cipherand solve ECDLP:. Clearly, it is difficult for Eve to derive the decryption key. In addition, it is well known that solving ECDLP is computationally infeasible. So no one can forgewithout knowing Bob’s private key. Proposition 2. After receiving the information, Bob authenticates the identity of the sender Alice by checking. Proof. The valueis the common session key of Alice and Bob. If Eve wants to impersonate Alice, Eve needs to derive Alice’s private keyor Bob’s private key. Eve faces the ECDLP again. Proposition 3. The proposed authentication protocol is deniable. Proof. Bob has the same ability as Alice to generate the authenticated information, sinceand. Thus, it cannot distinguish the authenticated informationwhether was sent by Alice or forged by Bob.This means that Bob can identify the source of the information but cannot prove to any third party that the information comes from Alice. Proposition 4. LetGbe a cyclic subgroup ofE(Fq) of large order. Suppose thatis a bilinear pairing on. Ifand, such thatand ifsandAare known, then the probability for findingCinGis negligible. Proof. Since, for nonzero integersaandb, the problem is also the discrete logarithmic problem. Proposition 5. The protocol can withstand a sender spoofing attack. Proof. Suppose that Eve intercepts the cipherand the authenticated information. Eve selects a random integerteto compute: Thus, Bob computes the pointsQeand. Letmebe a fake message from Eve. Eve creates whereXmay be the pointEve sendsto Bob. After receiving, Bob computesand, and checks whetherand. Only when both equations hold, Bob will accept the messageme. Proposition 6. The protocol can withstand a message modification attack. Proof. Suppose that Eve intercepts the authenticated information. Case 1. If Eve substitutesfor, whereand, after receiving the informationfrom Eve, Bob obtains a queer message, since.Afterwards, Bob computes the bilinear pairing.Thus, Bob rejects the messageme, since the value of the bilinear pairing. Case 2. If Eve substitutesfor, after receiving the informationfrom Eve, Bob computes the fake messageby using his private keytrand Alice’s public key. Bob will discover that. Also, Bob rejects the message. Proposition 7. (Completeness) If a sender and a receiver follow the proposed protocol to negotiate with each other, the receiver can identify the source of a message. Proof. It can be seen that the sender and receiver share the common session secret. Therefore, the receiver can identify the source of the messagemaccording to. In this section, we give a performance comparison of our protocol and other three deniable protocols in [4], [9], and [14].Table 1 shows that the computational cost of four deniable protocols. For convenience, the following notation is used:This the time for executing a Hash function;Tiis the time for executing a modular inverse operation;Tbpis the time for executing a bilinear pairing operation;Tpmis the time for executing a point multiplication operation;Tenis the time for executing an encryption;Tdeis the time for executing a decryption. It is well known that pairing operations are more expensive than point multiplications. For example, if the orderis a 160-bit prime andqis a 512-bit prime, then the performance simulation result in [15] indicates that the cost of oneTbpis about 7 times of that of oneTpmand 15 times of that of oneTh,respectively. The other operations applied in the protocols of Table 1 are negligible compared with them. Thus, the total computational cost (noTenandTde) of the protocols[4],[9],[14]and ours are approximately 5.14Th, 20.3Th, 19.33Th, and 21.3Th,respectively. Table 1: Computational cost In Table 2, we give a comparison of security. Kar’s protocol[9],[10]is insecure. R. Luet al.’s protocol[4]fails to achieve the second requirement of the deniable authentication scheme[5]. Table 2: Security In this paper, we presented an optimized non-interactive deniable authentication protocol based on elliptic Diffie-Hellman and bilinear pairing. It guarantees mutual and deniable authentication as well as confidentiality. To the best of our knowledge, only a few of the deniable protocols have a mechanism for mutual authentication. In 2013, J. Kar proposed an efficient mutual deniable authentication protocol. However,this protocol still has some security vulnerabilities. It cannot resist sender spoofing attack and message modification attack.As can be seen from Table 2, the proposed protocol is more secure than other protocols.3. Related Works
3.1 Kar’s Protocol


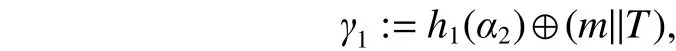
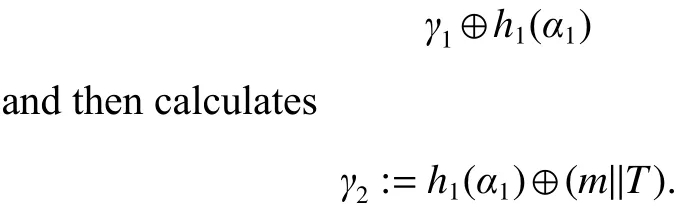
3.2 Sender Spoofing Attack

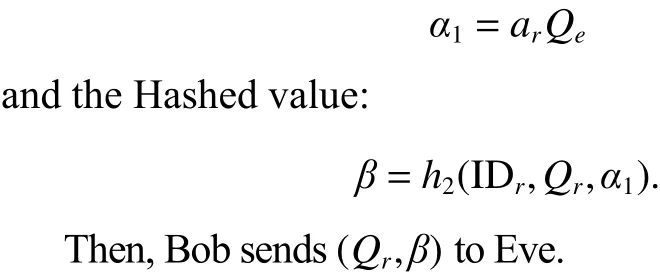

3.3 Message Modification Attack
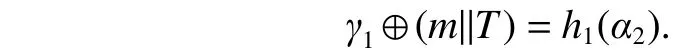
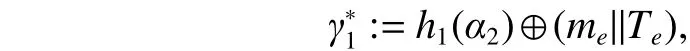

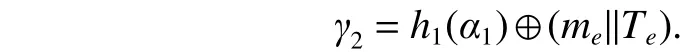
4. Proposed Protocol

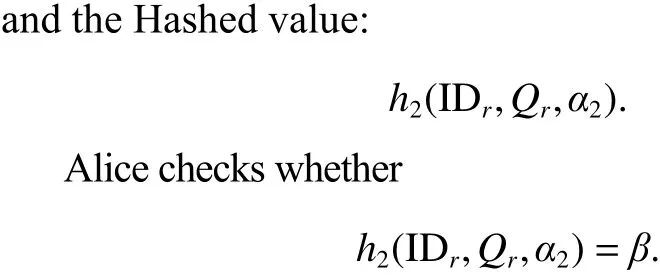

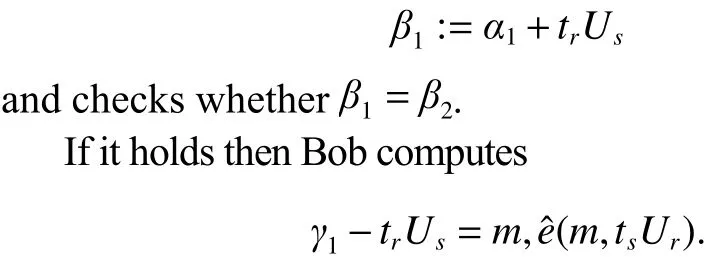
5. Security Analysis
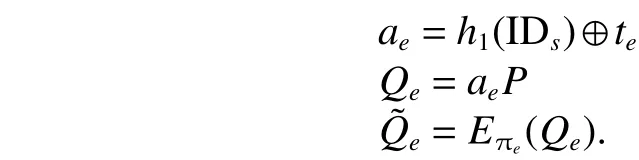

6. Comparison

7. Conclusions
 Journal of Electronic Science and Technology2018年2期
Journal of Electronic Science and Technology2018年2期
