奏响“创新型解析”的集结号
山东 尹承利
由《教学考试》杂志社主办的原创研发项目,为我们提供了广阔的教育、教研平台,基于学生思维过程展开的“创新型解析”模式,犹如出水的芙蓉,为“原创、研发”增添了一道亮丽的风景线,它更像声声催人奋进的战鼓,为老师们的自我展示奏响了集结号.“让解析成为原创题的闪光点和深入点”已成为我们数学原创研发团队老师们的共识!那么,如何进行原创题的创新解析?又以什么样的形式创新解析?笔者就参与“创新型解析”的过程和实践,并结合第二阶段的原创试题,谈一谈感悟和认识.
一、创新模式,花开别样
“坚持能力立意、诉诸试题本源、突破传统模式”应是“创新型解析”的切入点,“以生为本、展示能力递进关系、促进学生思维素养的发展”应是“创新型解析”的落脚点.
1.客观题模式

( )
A.(1,2)
B.[-2,2)
C.[-2,2]
D.(-2,2)
【创新解析】
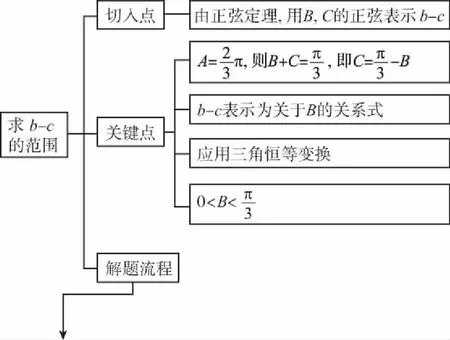
【备考点睛】解题的关键是先由正弦定理表示b,c,再通过三角恒等变换将b-c表示为角B的函数,再求最值.解决此类题要掌握正余弦定理,熟练边角互化以及三角公式的灵活应用.
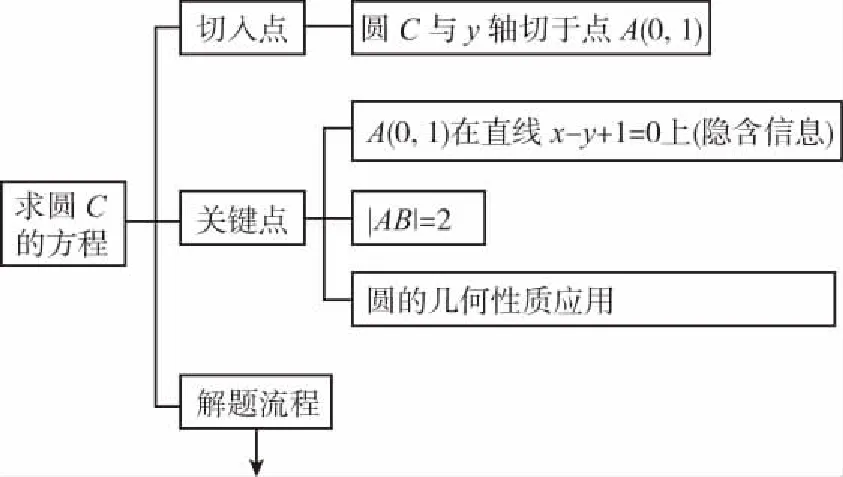
示例2.(原创卷)已知圆C的圆心在第一象限,若圆C与y轴相切于点A(0,1),与直线x-y+1=0的一个交点为B,|AB|=2,则圆C的标准方程是
( )
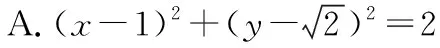
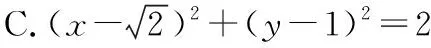
【创新解析】
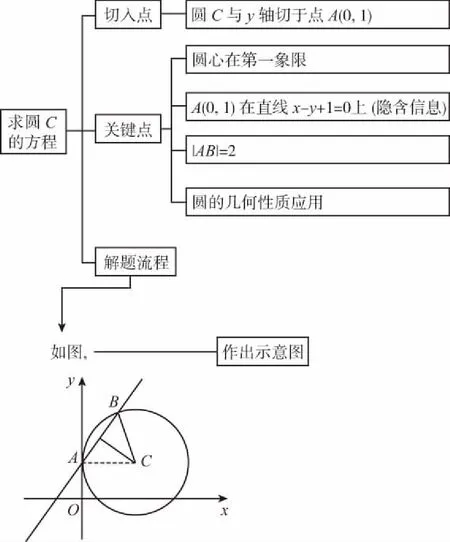
设圆C的半径为r,
设出圆心坐标
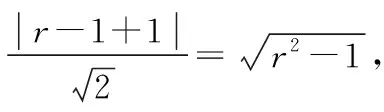
【备考点睛】解决此类题的关键是设出所求圆的圆心坐标和半径,列出方程(组),即可解得所求圆的标准方程.
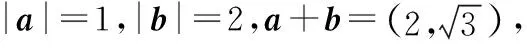
【创新解析】
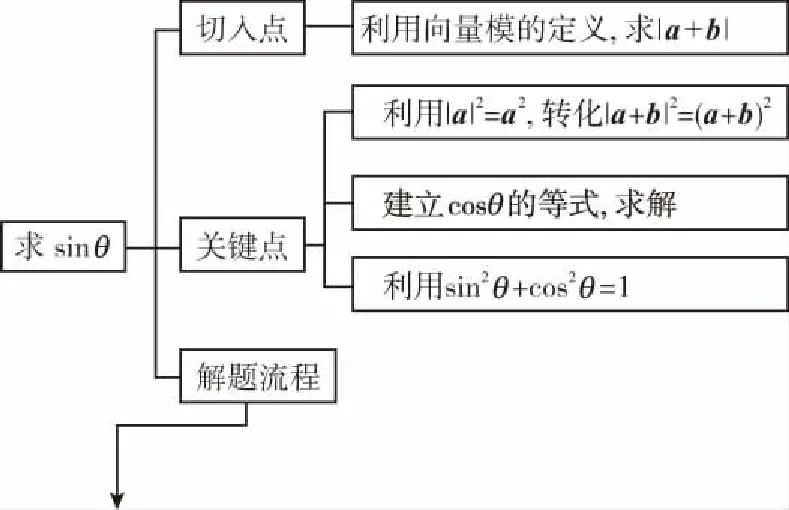
因为|a|=1,|b|=2,所以|a+b|2=
(a+b)2=a2+2a·b+b2=1+2×1×

a2和数量积
定义转化
【备考点睛】本题涉及到两个向量的模和夹角,利用向量模的公式、两个向量数量积的定义及|a|2=a2的转化是求解的关键.
2.解答题模式
示例4.(原创卷)已知动圆P过点A(2,0),且被y轴截得的线段长为4,记动圆圆心P的轨迹为曲线C.
(1)求曲线C的方程;
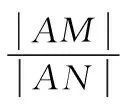
【创新解析】
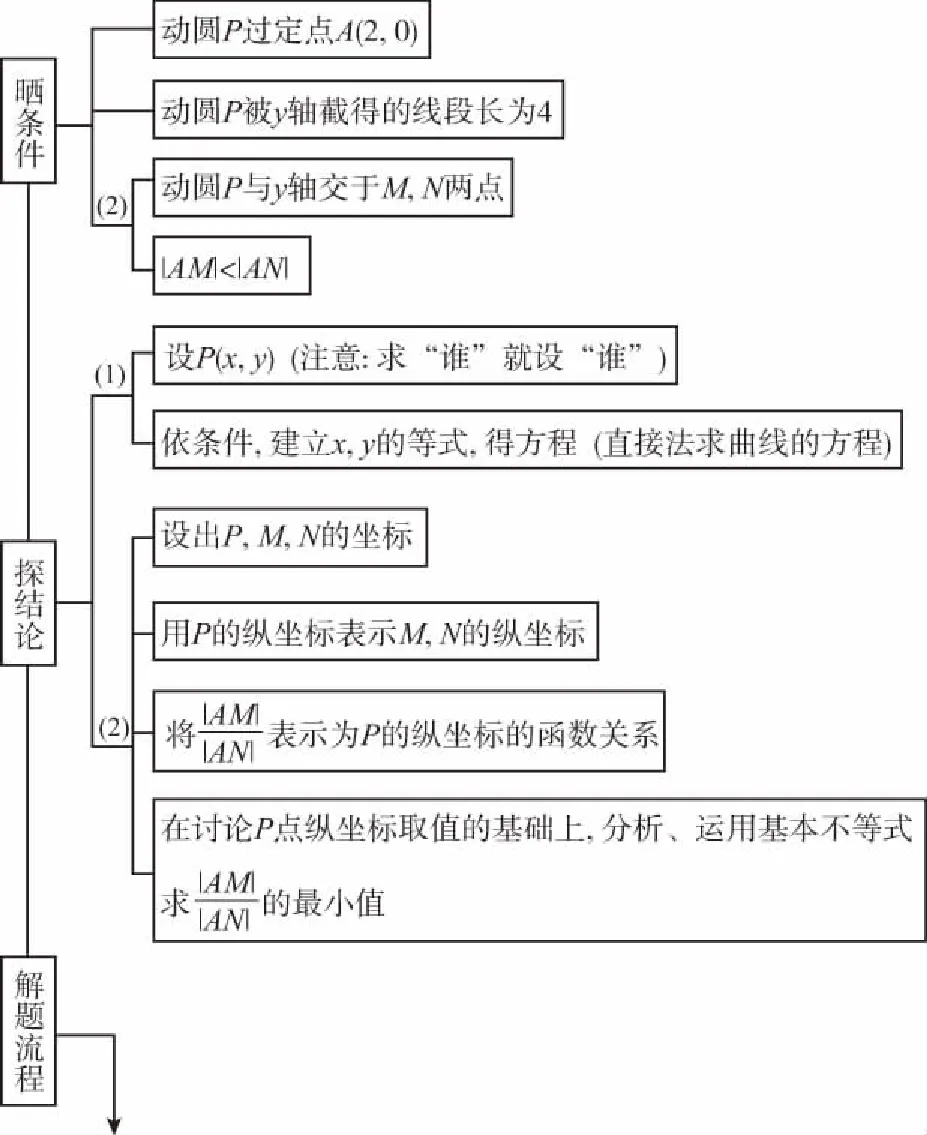

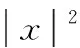
当y0>0时,y1=y0-2,y2=y0+2.
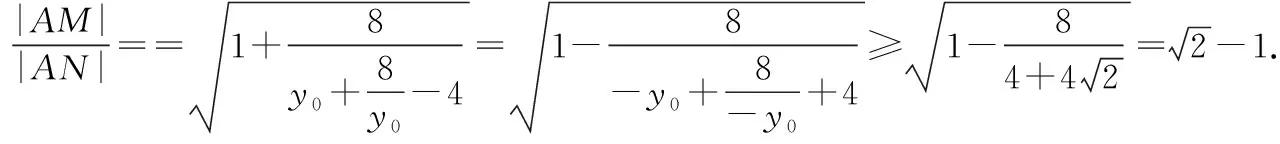
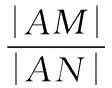
【备考点晴】解析几何的核心就是用方程的思想研究曲线,用曲线的性质研究方程.轨迹(曲线)问题正是体现这一思想的重要表现形式,探求轨迹(曲线)的方程是解析几何的基本问题之一,历年都是高考的热点.求轨迹(曲线)方程的常用方法有:直接法、代入法、定义法、参数法、交轨法等.
解析几何中的最值是高考的热点,在圆锥曲线的综合问题中经常出现,求解此类问题的一般思路是在深刻认识运动变化的过程之中,抓住函数关系,将目标量表示为一个(或者多个)变量的函数,然后借助于函数最值的探求来使问题得以解决.
示例5.(原创卷)已知函数f(x)=xex+a(x+1)2,a∈R.
(1)求函数f(x)的单调区间;
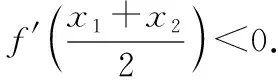
【创新解析】
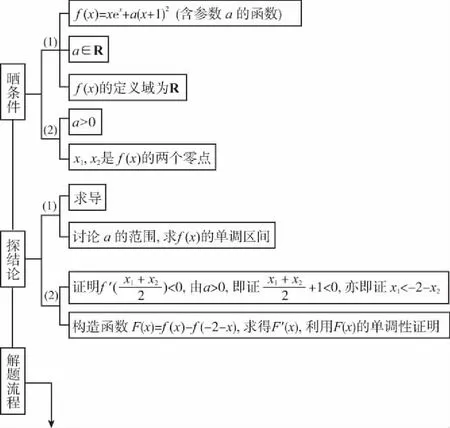
(1)因为f(x)=xex+a(x+1)2,所以

求导
①当a≥0时,ex+2a>0,
令f′(x)>0,解得x>-1;
令f′(x)<0,解得x<-1.

两类讨论

准确、全
面写出单
调区间
(2)当a>0时,由(1)可知,f′(x)=(x+1)(ex+2a)在区间(-1,+∞)上单调递增,在区间(-∞,-1)上单调递减,不妨设x1<-1 令F(x)=f(x)-f(-2- x)=xex+a(x+1)2-[(-2- x)e-2-x+a(-x-1)2]=xex+ 0,亦即证x1<-2-x2 因为F′(x)=(x+1)(ex- e-x-2)>0,所以F(x)在(-∞, -1)上单调递增,所以 调性,进而确定出 F(x)的范围 所以f(x) x)(x<-1),所以f(x1)< x)<0,代换得到f(x1)< f(-2-x1) 【备考点晴】本题主要考查的是利用导数研究函数的单调性、利用导数研究函数的零点,属于难题.利用导数研究函数f(x)的单调性进一步求函数最值的步骤:①确定函数f(x)的定义域;②对f(x)求导;③令f′(x)>0,解不等式得x的范围就是递增区间;令f′(x)<0,解不等式得x的范围就是递减区间;④根据单调性求函数f(x)的极值及最值(闭区间上还要注意比较端点处函数值的大小). 解析后的“加选条目”,既是对解析的进一步深化,又是一个再创造的过程.通过添加知识拓展、方法归纳、易错点拨、课本溯源、变式探究、考向分析及链接高考等栏目,启迪、引导学生拓展思维,达到由此及彼、触类旁通,从而进一步促进学生数学素养的提高. 示例6.(原创卷)复数z满足z·i=3-i,则复数z的虚部为 ( ) A.-1 B.3 C.-3 D.-3i 【考向分析】对于复数、几何表示、共轭复数、复数相等等基本概念和运算都是核心,可能沿袭这样的思路,in没有考查过,这需要引起注意. 示例7.(见示例1). 【知识拓展】辅助角公式: 示例8.(见示例2). 【方法归纳】求解直线与圆的位置关系问题时,为避免计算量过大,要数形结合,充分运用圆的几何性质.比如,圆心在圆的任一条弦的垂直平分线上;计算弦长时,可用半径、弦心距、半弦长构成直角三角形;涉及到圆的切线时,要考虑过切点与切线垂直的半径等. 【变式探究】若圆C与y轴相切于点A(0,1),与直线x-y+1=0的一个交点为B,|AB|=2,则圆C的标准方程是_______. 【创新解析】
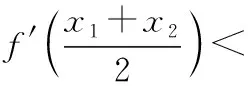


二、加选条目,锦上添花
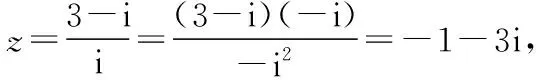
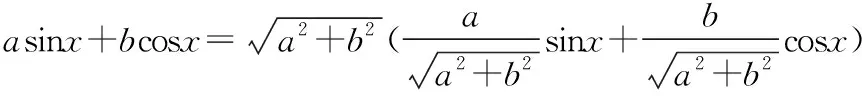
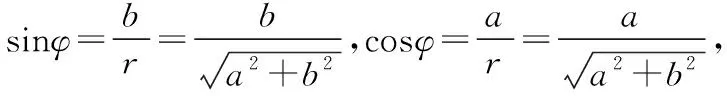
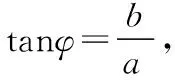


三、创新解析,绵绵未了

——记我的原创感悟

