翼尖尖点散射特性分析*

(中航工业第一飞机设计研究院，西安 710089)

1 引 言

随着探测技术和雷达制导武器的迅猛发展，未来作战飞机越来越重视隐身技术的应用。现代作战飞行器上采用隐身技术已经成为不可逆转的趋势，并已成为作战飞机的基本要求。在雷达隐身方面，采用外形隐身技术控制三大强散射源(雷达天线舱散射、进气道腔体及发动机压气机散射、座舱散射)、采用雷达吸波材料等技术措施降低雷达截面(Radar Cross Section,RCS)是实现隐身的主要技术途径。但在解决以上问题后，对于极低RCS隐身飞行器而言，并未解决隐身问题的全部。当强散射源解决后，次散射源又变成了新强散射源，如飞行器机头的尖顶绕射、外露天线、机翼翼尖等尖点绕射。如果不加以控制，一组翼尖散射就足以破坏飞行器的隐身性能，何况飞行器存在成百上千的缝隙和台阶等弱散射源。据统计，飞机表面的弱散射源，其前向RCS可以达到1 m2，导致不能实现极低RCS隐身飞行器的隐身目标。这是隐身技术必须解决的问题之一。

鉴于飞行器隐身技术的敏感性，从公开发表的文献中，国外关于隐身飞机弱散射研究的相关成果和论文很难检索到。在国内，关于飞行器表面弱散射源对RCS的影响研究主要集中在电磁缺陷方面，且以缝隙、台阶以及铆钉等散射源缩减为主。例如：文献[1-4]通过钻石体(一种低RCS载体)RCS实验，初步研究了缝隙、台阶等弱散射源的雷达电磁波后向散射问题，提出了飞行器表面电磁缺陷的概念和初步的控制方法；文献[5]比较系统地对飞行器电磁缺陷进行了分析；文献[6]对隐身飞机机身侧棱电磁散射特点进行了分析，但是针对机翼尖点散射特性分析得比较少,并且所采用的算法精度比较差。

本文针对典型机翼，拟设计几种不同的典型翼尖外形方案，采用精度更高的计算方法——多层快速多级子算法(Multilevel Fast Multipole Algorithm，MLFMA)，仿真分析了不同机翼翼尖外形在不同频段、不同方位角度条件下对其雷达散射特性影响，通过对比分析优选出最佳的低RCS翼尖外形方案。

2 翼尖外形方案

为了研究翼尖尖点绕射灯弱散射问题，选取了一种典型翼尖进行研究，图1给出了翼尖示意图(红色圆圈)。

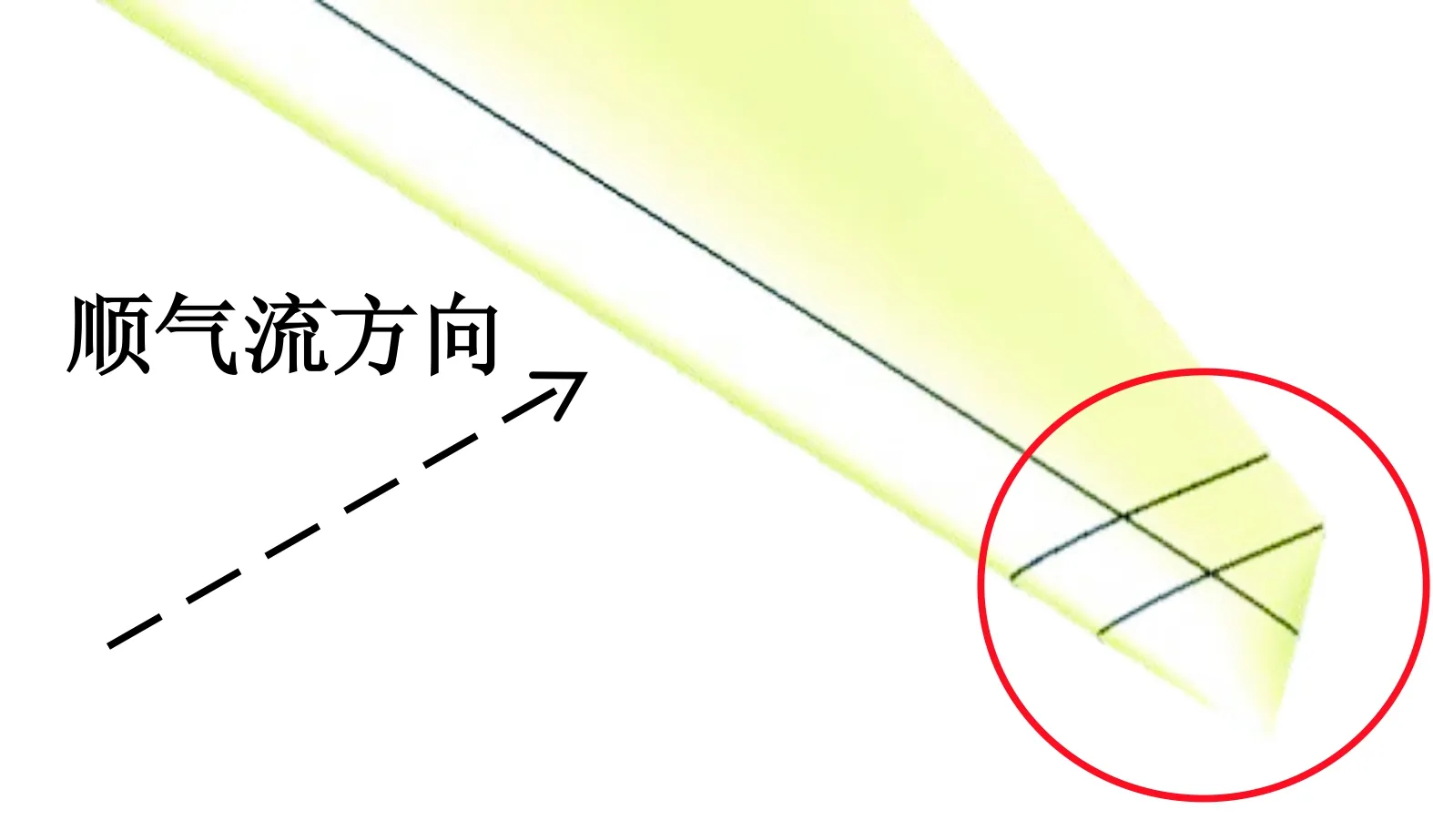
图1 翼尖示意图(红色圆圈)Fig.1 Wing tip schematic(red circle)

为了尽可能消除翼根带来的影响，对翼根进行了低RCS修形处理，并且对原始翼尖分别进行了顺气流直切(黑色虚线)和平行于某部件前缘斜切处理(红色虚线)。图2所示为3种不同翼尖方案外形示意图。

图2 不同翼尖形式示意图Fig.2 Different wing tip schematic

3 研究理论

3.1 计算方法

本文采用的多层快速多极子方法是一种快速有效的求解电磁散射的方法，具有计算能力稳定、速度快、精度高等特点[7-9]。通过多层快速多极子方法求解混合场积分方程(Combined Field Integral Equation，CFIE)并选择RWG型基函数计算目标表面电流分布，采用下式计算散射场和雷达散射截面：

(1)

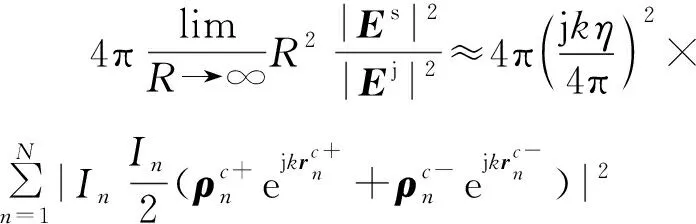
(2)

σ*≈10lgσ。

(3)

式中：Es为雷达接收处的散射电场，Ej为目标处的入射电场，σ为雷达散射截面(单位m2)，σ*为雷达散射截面(单位dBsm)。

利用基于多层快速多极子算法的FEKO软件，采用远场平面波照射，计算类型为单站RCS，极化方式为水平极化(HH)和垂直极化(VV)，计算方位角为0°～180°，计算步长为1°，其中0°方位角定义为电磁波从机头沿飞机轴线向后照射。

3.2 计算结果验证

为了验证MLFMA对尖点绕射尖点和前缘行波散射等弱散射的精度，设计了一个低RCS载体[4]，如图3所示。拟通过理论计算和试验两种方法对比分析不同横向缝隙在15°内的RCS误差范围。

图3 低RCS载体试验件Fig.3 The low RCS carrier

图4给出了9.41 GHz频段仿真和试验数据。从图4可以看出，在方位角15°范围，两种横向缝隙的RCS值变化基本趋于一致，说明该理论算法和计算结果是正确可行的。

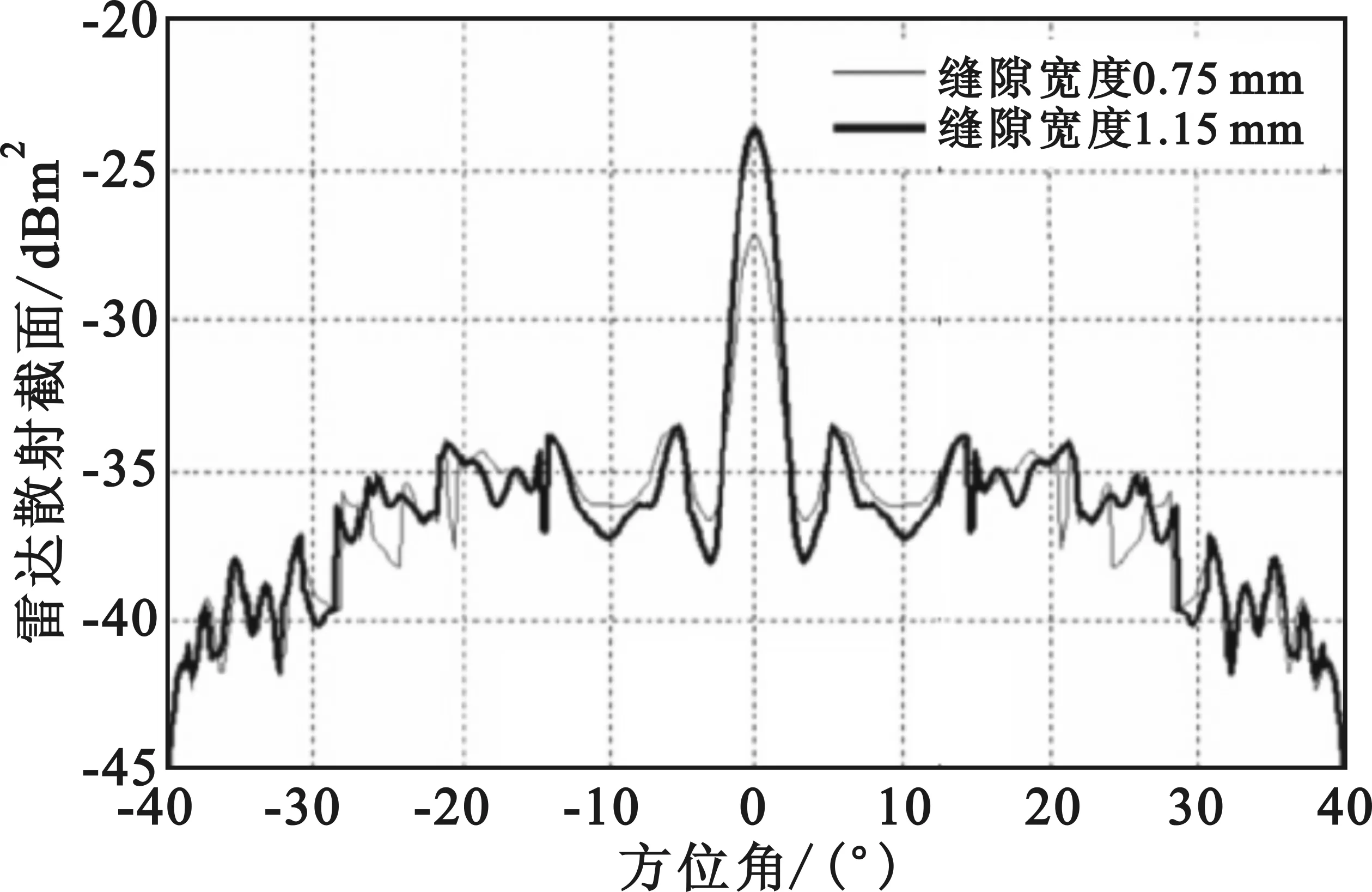
(a)横向缝隙计算结果(垂直极化方式)

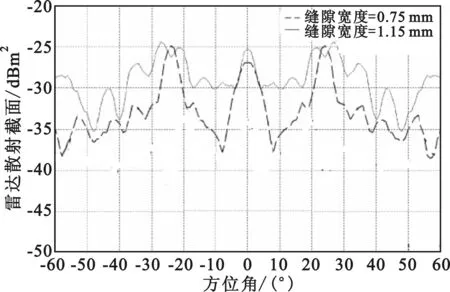
(b)横向缝隙试验结果(垂直极化方式)图4 9.41 GHz频段仿真和试验数据对比Fig.4 9.41 GHz spectrum simulation and comparison of experimental data

由于缝隙散射和尖点散射都属于弱散射范畴，故该方法对尖点散射的仿真计算也同样是适用的。

4 计算分析

4.1 3种不同翼尖外形对比分析

利用上述方法的FEKO软件对3种不同翼尖外形进行仿真计算分析，分别计算1 GHz、9.41 GHz、18 GHz 3个频点在方位角为0°～180°、俯仰角为0°范围内的RCS值。

图5～7分别给出了1 GHz、9.41 GHz和18 GHz频点的3种不同翼尖外形的RCS曲线。

(a)水平极化方式(HH)的RCS分布曲线

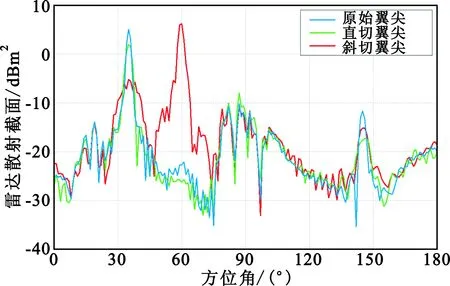
(b)垂直极化方式(VV)的RCS分布曲线图5 1 GHz频点的3种不同机翼翼尖的RCS曲线Fig.5 The RCS curve of different wing tip at 1 GHz

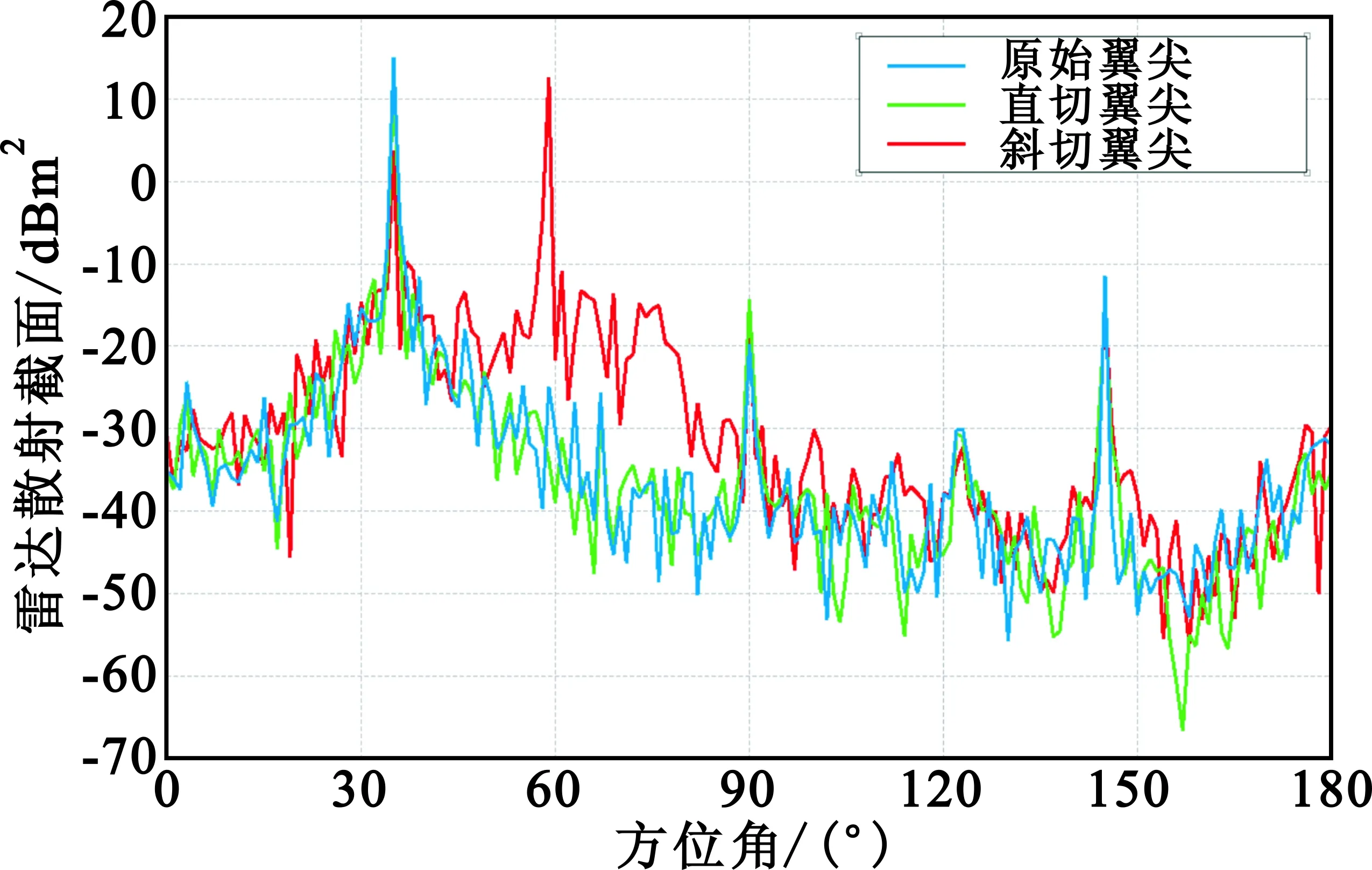
(a)水平极化方式(HH)的RCS分布曲线

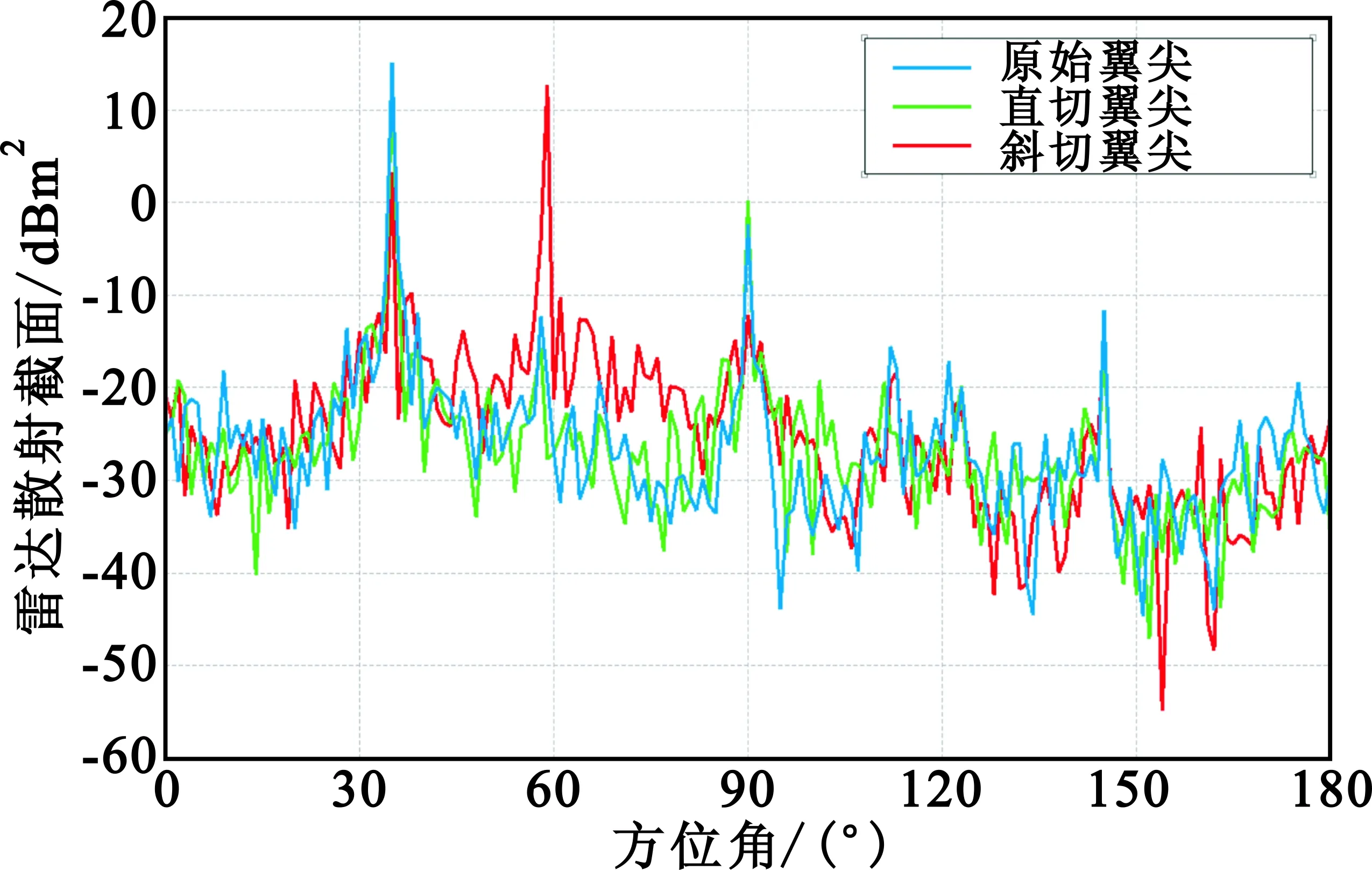
(b)垂直极化方式(VV)的RCS分布曲线图6 9.41 GHz频点的3种不同翼尖外形的RCS曲线Fig.6 The RCS curve of different wing tip at 9.41 GHz

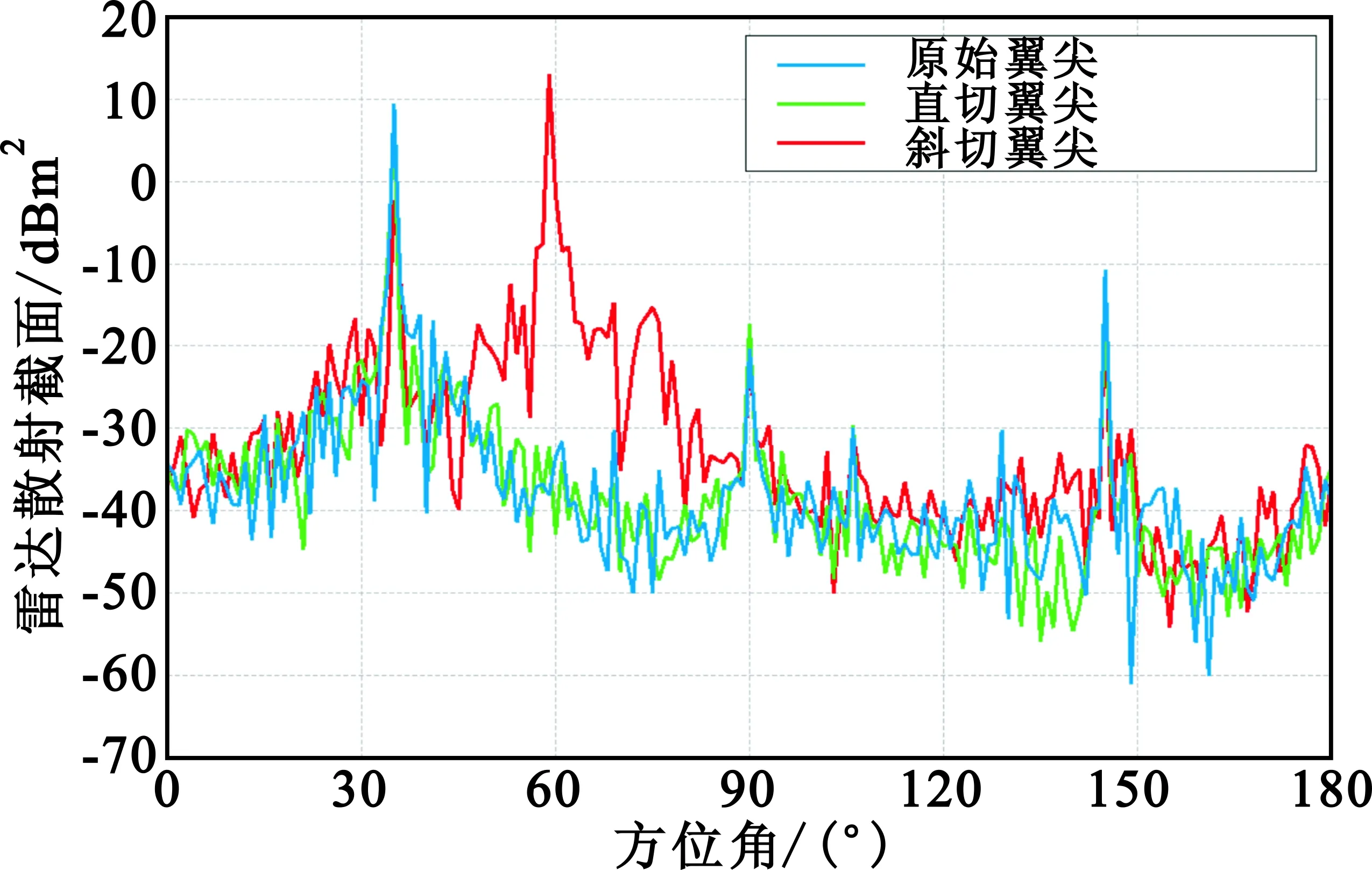
(a) 水平极化方式(HH)的RCS分布曲线

(b)垂直极化方式(VV)的RCS分布曲线图7 18 GHz频点的3种不同翼尖外形的RCS曲线Fig.7 The RCS curve of different wing tip at 18 GHz

通过仿真对比分析，从以上3种不同翼尖外形的RCS曲线及前向、后向不同方位角范围内的RCS均值，可以得出：

(1)在低频段，VV极化RCS要优于HH极化；在高频段，HH极化RCS要高于VV极化；

(2)在3种翼尖中，斜切翼尖在方位角60°附近处产生了一个波峰；

(3)对比3种不同翼尖均值、波峰数量等，直切翼尖RCS均值在前后向30°范围内总体要低于原始翼尖、斜切翼尖。

4.2 6种不同属性的直切翼尖外形对比分析

由上面的仿真结果可知，直切翼尖对前向RCS贡献较小。为了进一步分析直切翼尖对RCS的影响，选择了不同直切范围的翼尖方案(从翼尖到翼根纵向平行切割)。同样，拟通过仿真手段，对其不同翼尖进行RCS分析，优选最佳的低RCS直切翼尖。

在原始机翼翼尖基础上，沿着翼尖纵向方向分别进行了展长为5%、10%、15%、20%、25%、32%纵向距离顺气流直切，如图8所示，图中红色虚线为切割线。

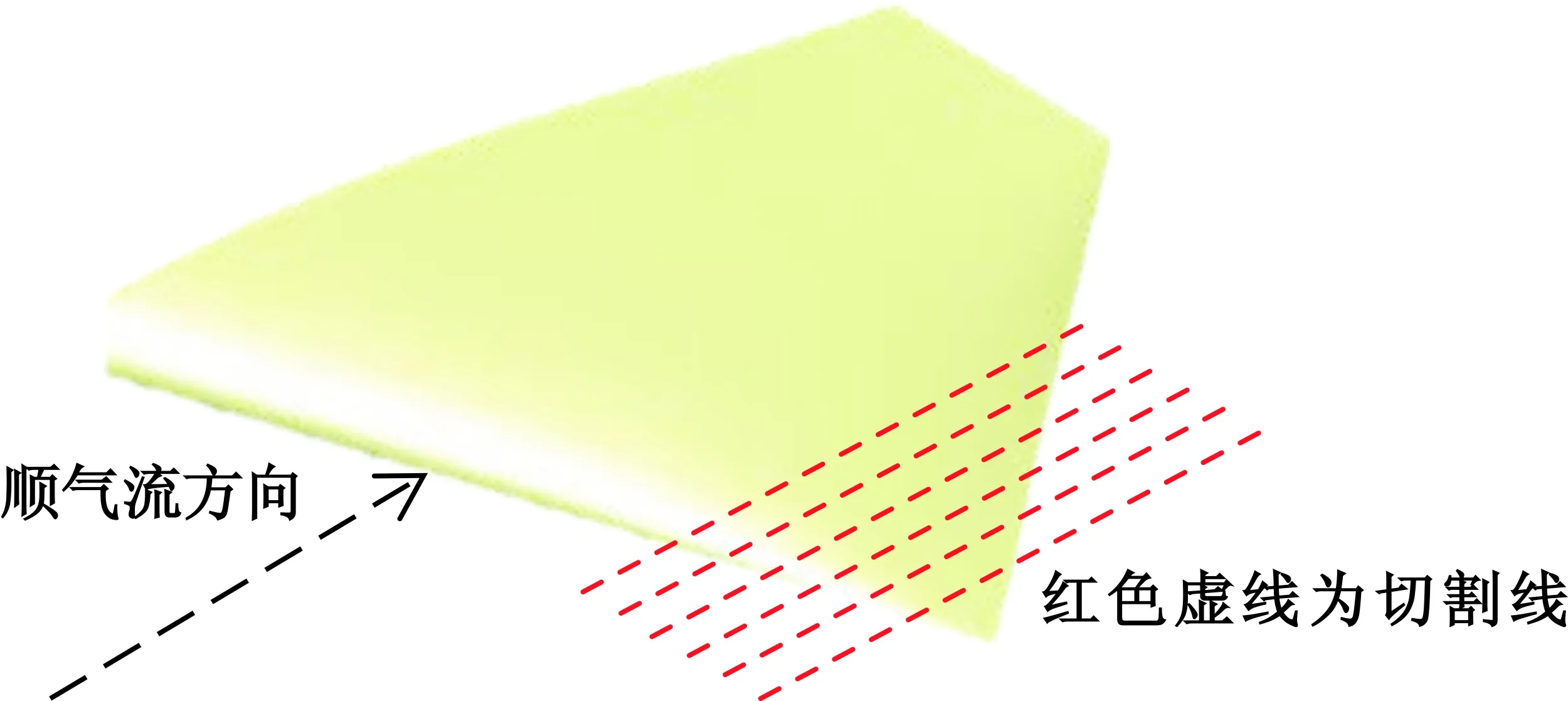
图8 不同直切属性的翼尖Fig.8 The different straight cut wing tip

利用上述方法计算方位角0°～180°、俯仰角0°范围的RCS(飞机前向为0°方向)，其仿真频率分别为1 GHz、9.41 GHz、18 GHz。

图9和图10分别给出了500 MHz和1 GHz频点的6种不同直切翼尖的RCS曲线(水平极化方式)。

图9 500 MHz频点6种不同直切翼尖的RCS曲线Fig.9 The RCS curve of wing tip at 500 MHz

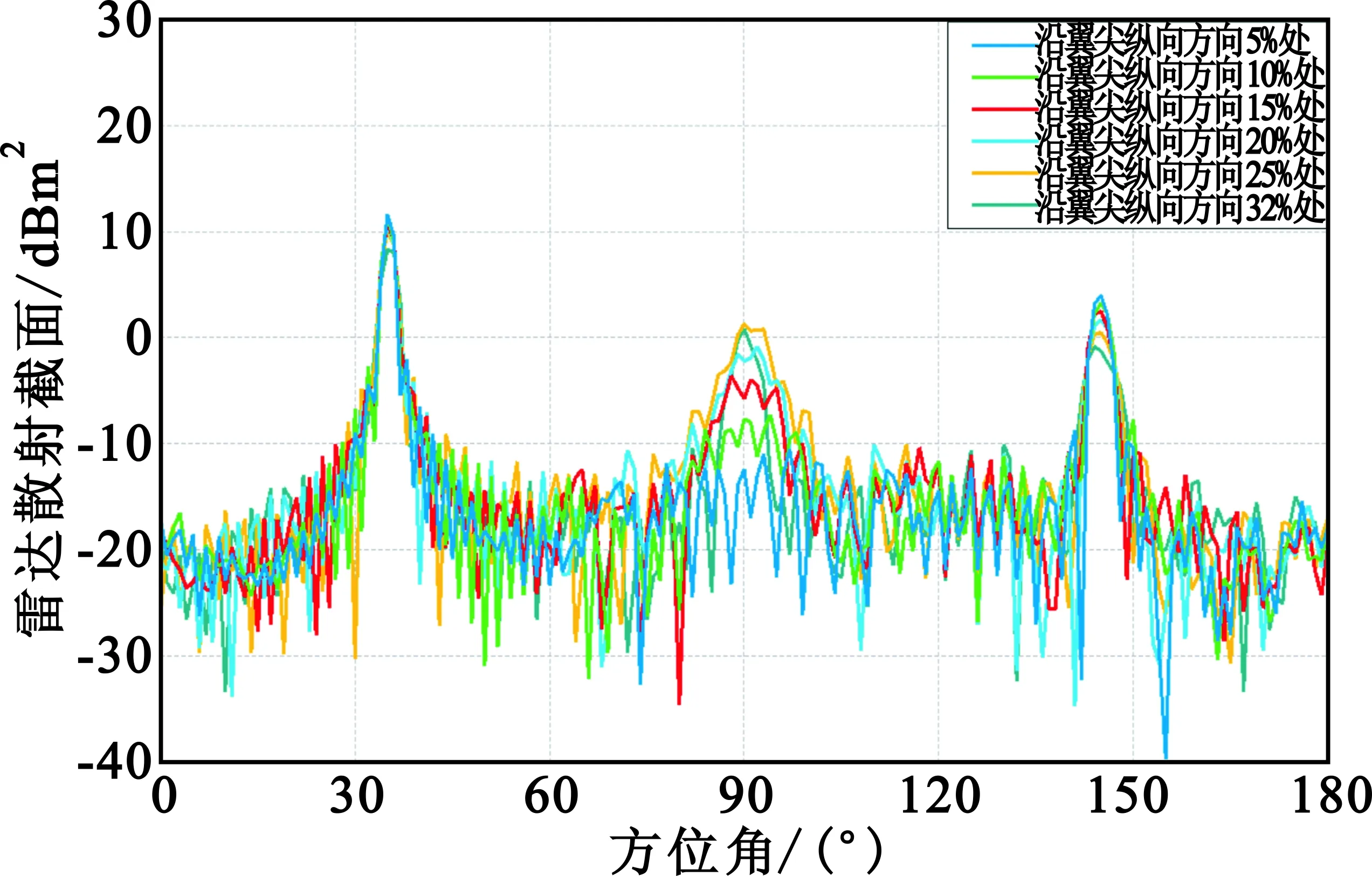
图10 1 GHz频点6种不同直切翼尖的RCS曲线Fig.10 The RCS curve of wing tip at 1 GHz

图11和图12分别给出了9.41 GHz和18 GHz频点的6种不同直切翼尖的RCS曲线。

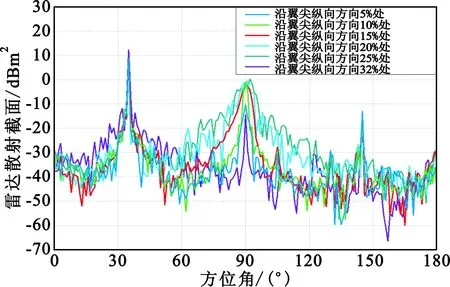
(a) 水平极化方式(HH)的RCS分布曲线

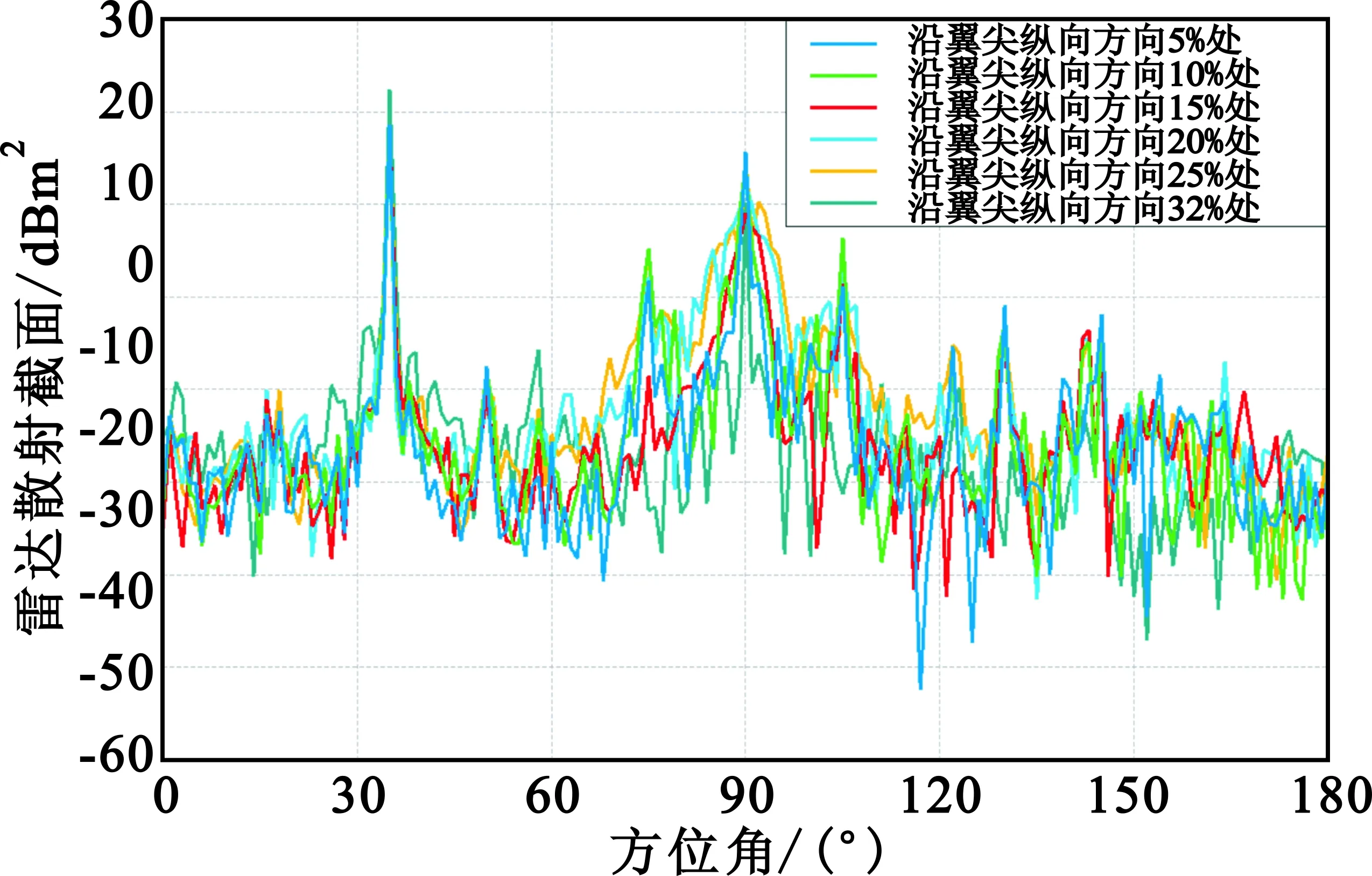
(b)垂直极化方式(VV)的RCS分布曲线图11 9.41 GHz频点6种不同直切翼尖的RCS曲线Fig.11 The RCS curve of wing tip at 9.41 GHz

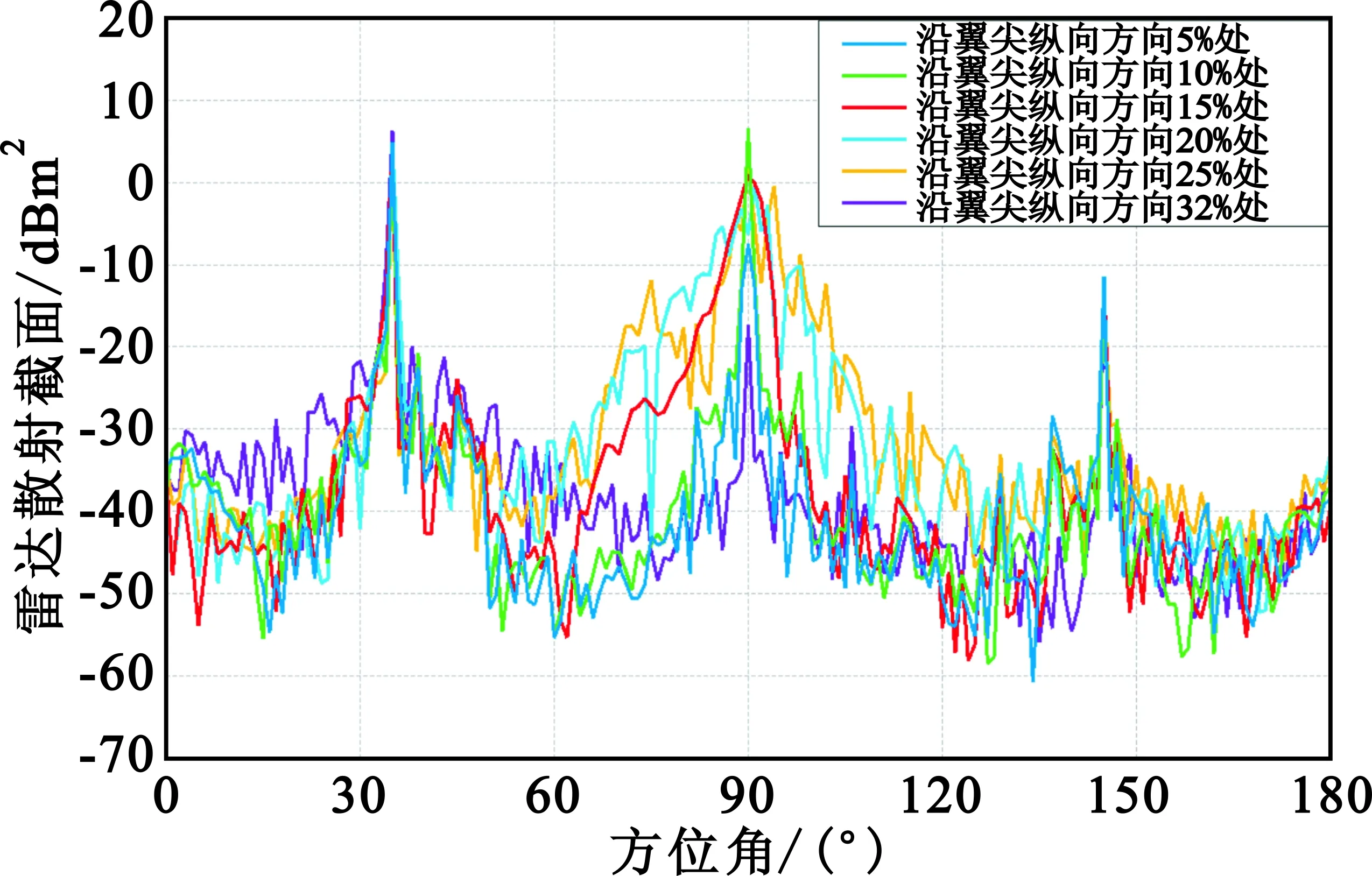
(a)水平极化方式(HH)的RCS分布曲线

(b)垂直极化方式(VV)的RCS分布曲线图12 18 GHz频点6种不同直切翼尖的RCS曲线Fig.12 The RCS curve of wing tip at 18 GHz

5 结束语

对比分析上述3种不同翼尖外形方案及6种不同直切翼尖方案的RCS曲线、峰值以及不同方位角范围内的均值等参数(见第4节)，可以得出以下结论：

(1)在小角度方位角范围内，HH极化RCS均值要优于VV极化;在大角度方位角范围内，VV极化RCS均值要优于HH极化。

(2)纵向15%直切翼尖在前向30°范围内RCS均值总体要低于其他5种直切翼尖。

(3)纵向15%直切翼尖在后向30°范围内，在低频段，RCS均值总体要低于其他5种直切翼尖；在高频段，纵向10%直切翼尖RCS均值总体要低于其他5种直切翼尖。

(4)纵向15%直切翼尖其RCS贡献远小于原始翼尖；在小角度方位角范围内，其最大收益可以降低11 dB。

(5)频率越高，外形的要求越高，从高频段90°附近峰值上扬可以看出，外形对其RCS影响较大。

(6)从翼尖到翼根方向上15%处顺气流直切的翼尖外形方案其翼尖尖点所带来的RCS贡献最小。

(7)直切翼尖外形隐身效果较优，该种翼尖也比较符合目前主流战斗机的翼尖(如F22等)。

但是，由于对翼尖进行了简化，是否能在全尺寸机翼或者飞机上有较好的RCS收益，则需要进一步在全尺寸机翼上进行对比分析，甚至要进行RCS测试验证。