一种多用户MIMO系统干扰对齐优化算法*

陈 艳**，2，宋云超

(1.南京邮电大学 电子与光学工程学院、微电子学院，南京 210003；2.南京理工大学紫金学院 电子工程与光电技术学院，南京 210046)

1 引 言

作为第四代蜂窝移动通信系统的关键技术之一，多输入多输出(Multiple-Input Multiple-Output，MIMO)技术在不增加系统带宽和天线发射功率的前提下可以显著提高信道的容量及频谱利用率[1]。单用户MIMO系统若配置的天线数受限会降低系统获得的容量增益，而多用户MIMO系统允许多个用户同时进行通信，可达到更高的容量，但当天线数目及用户数量增加时会引起无线介质的广播与叠加，此时干扰成为制约多用户MIMO系统可靠通信的重要因素之一[2]。因此，为了改善系统的性能，需要采用有效的措施对用户引起的干扰进行管理。

干扰对齐(Interference Alignment，IA)被认为是处理多用户MIMO系统用户间干扰的关键技术之一，并已经被证实可有效获得网络的最大自由度[3]。干扰对齐技术可广泛应用到各种网络拓扑中，如干扰信道[4-8]、干扰多址接入信道[9]、干扰广播信道[10]、具有中继的信道[11]等。

现有的多用户MIMO系统干扰对齐算法主要分为两类：基于信号空间的干扰对齐算法与基于信号尺度的干扰对齐算法。基于信号尺度的干扰对齐算法因难以精确跟踪信道变化均实用性较差。基于信号空间的干扰对齐算法为了实现干扰对齐，必须联合设计发送预编码矩阵与接收侧的干扰抑制矩阵，但一般是非凸问题很难求解。在实际中经常采用迭代的方法来求解发送预编码矩阵与接收侧的干扰抑制矩阵。

目前基于迭代的干扰对齐算法在高信噪比下性能较优越，但由于实际应用场景如小区边缘信噪比较低，因此中低信噪比区域的性能是实际无线系统干扰对齐最具潜在的应用，具有较大的研究意义。基于迭代求解预编码矩阵与接收侧的干扰抑制矩阵的方法主要有最小干扰泄露算法[12](Minimum Weighted Leakage Interference，Min-WLI)、最大信干噪比算法[12](Maximum Signal-to-Interference-plus-Noise Ratio，Max-SINR)、最小均方误差算法[13](Minimum Mean Square Error,MMSE)，但是，最小干扰泄露算法未考虑噪声的影响，因此在中低信噪比时可达的和速率并不是最佳的；最大信干噪比算法在中低信噪比区域算法性能较优越，但算法的收敛性无法保证；最小化均方误差算法既可以使系统获得中低信噪比时的性能，又可以保证其收敛性，目前在迭代法中比较常用。本文采用的迭代方法以最小化均方误差作为优化准则。

所有迭代方法中首先都要对发送预编码矩阵进行初始化处理，目前预编码矩阵的初始化常有3种方法，即利用右奇异矩阵初始化[14]、利用确定的IA解[3]进行初始化、随机矩阵初始化[15-16]。这几种预编码矩阵的初始化方法对系统性能的影响是不同的[17]，其中利用确定的IA解进行初始化方法只能在一定条件下获得所以很少采用；随机矩阵初始化方法虽然实现简单但未考虑信道特性的影响；利用直通信道右奇异矩阵初始化的方法只考虑有用信号的影响而未考虑干扰的影响。而本文所提算法是在最小化均方误差算法的基础上对预编码的初始化值进行重新设计，设计过程中既考虑了干扰的影响也考虑了有用信号的影响。在算法具体实现过程中选取和MSE最小化作为优化目标，在处理时利用正交三角(Quadrature Rectangular，QR)分解将信道空间分为有用信号空间与干扰信号空间来进行预编码矩阵的初始化设计，然后将其固定，得到干扰抑制矩阵，再将干扰抑制矩阵固定得到预编码矩阵，经过反复迭代得到发送预编码矩阵与干扰抑制矩阵的最优解。

文中所使用的矩阵、向量等操作符号的含义：Id表示d×d的单位矩阵，AH、A-1与|A|分别表示矩阵A的共轭转置、逆与行列式，‖a‖2与‖A‖F分别表示向量a的2范数、矩阵A的Frobenius范数，Tr(A)、Rank(A)与E[A]分别表示矩阵A的迹、秩与统计期望。

2 系统模型

K(K≥3)用户MIMO干扰信道，每个用户包括一个发射机和相应的接收机，即用户k∈{1,2,…,K}由k个发射机与k个接收机组成，且发射机k只与接收机k进行通信。每个发射机的天线数为M，每个接收机的天线数为N，每个用户发送数据流的数目为d，K用户干扰信道系统模型如图1所示。

图1 K用户干扰信道系统模型Fig.1 System model for the K user interference channel

用户k接收的信号为

(1)

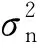
(2)

系统的和速率可以表示为

(3)

若完全删除干扰，预编码矩阵与干扰抑制矩阵必须满足下面的线性干扰对齐条件：

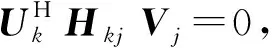
(4)

(5)

式(4)是干扰迫零条件，式(5)可以保证期望信道获得有效数据流的数目。当K、M、N、d满足某些约束时上述条件是可行的，一般仅当M+N-(K+1)d≥0时系统是合适的。为简化分析，此处假定系统是合适系统。预编码矩阵与干扰抑制矩阵在设计时有很多优化标准，本文重点探讨均方误差最小化的优化标准。

3 基于MSE的干扰对齐的迭代算法

3.1 问题描述

本文在设计K用户MIMO干扰信道的发送预编码矩阵及接收侧的干扰抑制矩阵时其优化目标及约束条件同文献[18],优化问题描述为

(6)

MSEk的表达式如式(7)所示：

(7)

利用拉格朗日乘子法可求得Vk和Uk的最优解为

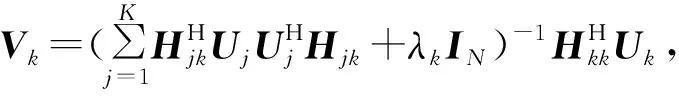
(8)

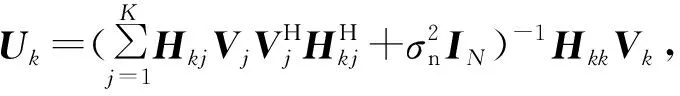
(9)

式中：λk为发射机k与功率约束相关的拉格朗日乘子。从式(8)～(9)可以看出，不能直接求解Vk和Uk，此处采用迭代的方法进行求解。

3.2 迭代算法描述

迭代算法步骤如下：

Step1 初始化发送预编码矩阵Vk。

Step2 将Vk代入式(9)优化接收侧的干扰抑制矩阵Uk。

Step3 将λk与Uk代入式(8)求取新的Vk。

Step4 重复Step 2～3直至收敛或者到预定义的收敛次数。

其中发送预编码矩阵初始化采用了右奇异矩阵初始化及随机矩阵初始化的方法[14,18],但这些方法未考虑到干扰信号的影响。

4 预编码矩阵初始值的重新设计

目前文献常用的随机矩阵初始化和右奇异矩阵初始化两种预编码矩阵初始化方法，前者未考虑信道特性的影响，而后者未考虑干扰信号的影响，因此提出一种新的预编码初始值设计的新方法，该方法考虑了干扰信号的影响。

4.1 第一个接收用户端预编码矩阵的设计

第一个用户接收端接收的信号可以表示为

(10)

式中：V1j表示第j个发送用户到第一个接收用户的预编码矩阵。

对H1j进行QR分解得

(11)

式中：R1j是M×M的上三角矩阵；Q1j是N×N的酉矩阵，其列向量是标准正交的。根据矩阵理论可知H1j与Q1j具有相同的统计特性，现将Q1j表示为

Q1j=[Q11j|Q21j] 。

(12)

式中：Q11j、Q21j分别为N×d、N×(M-d) 的矩阵，分别表示第j个发送用户到第1个接收用户发送信号的信号子空间的基向量和其正交子空间的基向量。要做到干扰对齐，必须将除第一个发送用户以外的发送信号子空间对齐到第一个发送用户对的正交子空间。因此，需要采用W1j(j≠1)对Q11j变换使其对齐Q211，即要求W1j使

(13)

由W1j的正交性有

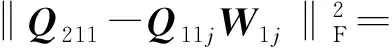
(14)

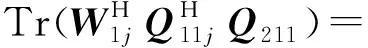
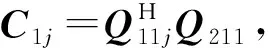
(16)

根据文献[19]得到

(17)

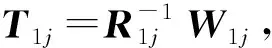
(18)

根据式(18)可求得除第一个发送用户以外的其他用户发送到第1个接收用户的预编码矩阵

(19)

4.2 第k(k>1)接收用户端预编码矩阵的设计

第k个用户接收端接收的信号为

(20)

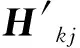
(21)

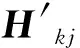
(22)

Qkj=[Q1kj|Q2kj] 。

(23)

式中：Q1kj、Q2kj分别表示第j个发送用户到第k个接收用户发送信号的信号子空间的基向量和其正交子空间的基向量。要做到干扰对齐，必须将除第k个发送用户以外的发送信号子空间对齐到第k个发送用户的正交子空间。因此，需要采用Wkj(j≠k)对Q1kj变换使其对齐Q2kk，即要求Wkj使

(24)

同第一个接收用户端预编码矩阵设计相似，求解上式时，可令

(25)

对Ckj作SVD分解:

(26)

利用文献[19]得到

(27)

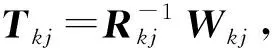
(28)

根据式(28)可求得除第k个发送用户以外的其他用户发送到第k个接收用户的预编码矩阵

(29)

根据上式可求得发送干扰用户到第k个接收用户的预编码矩阵，为简化分析，直通信道的预编码矩阵Vkk可假定为单位阵。

5 所提算法的收敛性能

MSE(Uk(n),Vk(n))≥MSE(Uk(n+1),Vk(n)) 。

(30)

当解出接收侧的干扰抑制矩阵Uk(n+1)后，利用式(8)可以更新发送侧的预编码矩阵，同理优化后系统均方误差和也不会增加，则有下式成立：

MSE(Uk(n+1),Vk(n))≥MSE(Uk(n+1),Vk(n+1)) 。

(31)

综合式(30)和式(31)可得到

MSE(Uk(n),Vk(n))≥MSE(Uk(n+1),Vk(n+1)) 。

(32)

在每次迭代过程中，均方误差和都不会增加，表明所提算法是收敛的，有一个局部最优解。

6 仿真结果与分析

本节对优化算法的性能进行分析，主要研究优化算法系统的收敛性能、MSE性能、和速率性能，其中系统的收敛性能主要研究迭代次数的变化对系统和速率的影响，MSE性能主要研究不同预编码初始化方法下信噪比的变化对均方误差和的影响。最后将本文所提算法与最小干扰泄露算法、最大信干噪比算法进行对比分析。具体仿真环境如下：所有用户的功率等功率分配，即Pk=P,∀k，用户数为3，发送端天线数为2，接收侧天线数为6，每个用户发送数据流的个数为2。以上数据符合合适系统的条件，仿真中的信道模型采用瑞利平坦衰落信道，均方误差和与系统的和速率值均取的是1 000次信道实现的均值，仿真参数如表1所示。

表1 仿真参数Tab.1 Simulation parameters

6.1 收敛性能分析

不同的迭代次数对系统和速率的影响如图2所示。

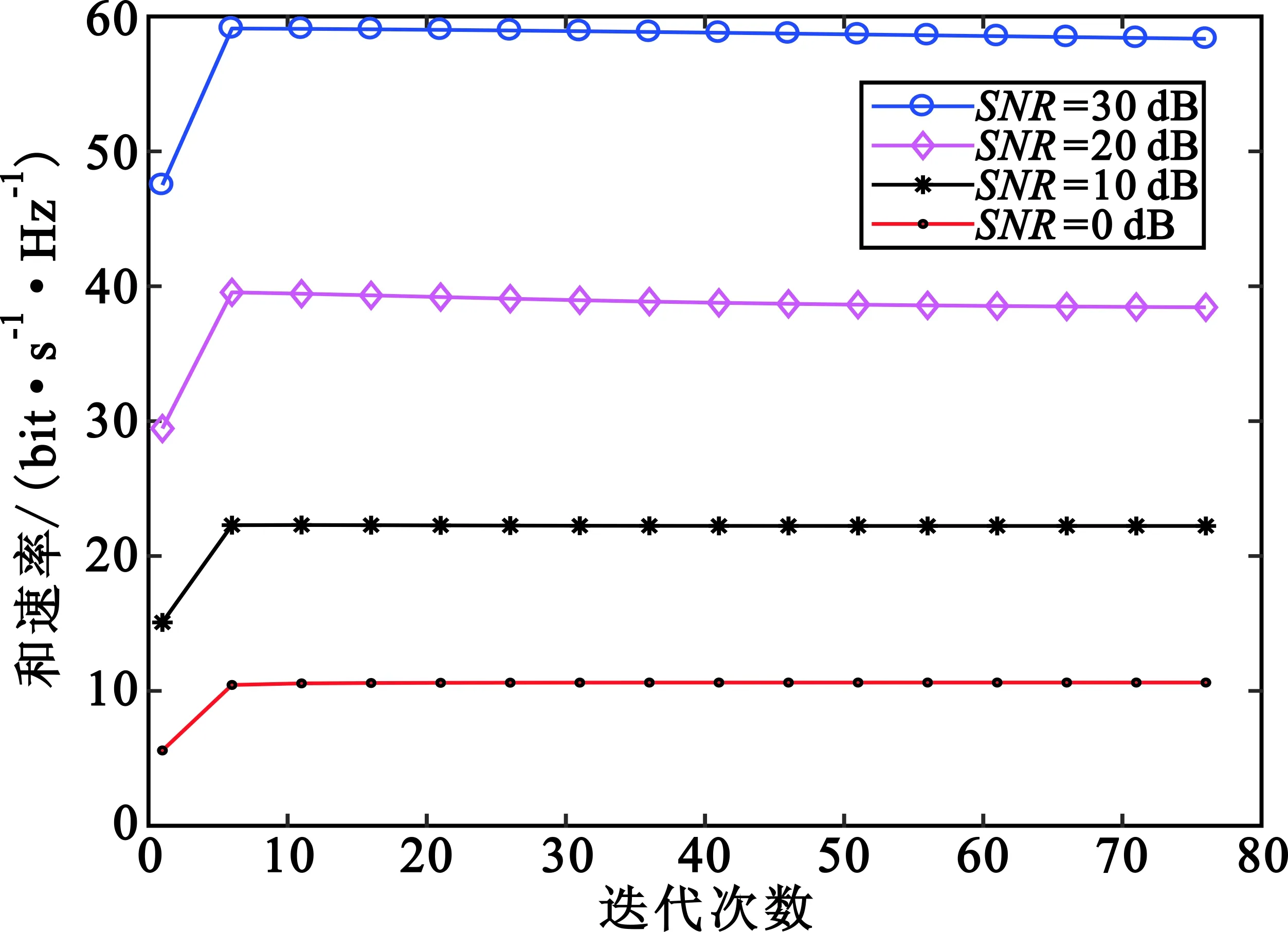
图2 不同信噪比下和速率与迭代次数的关系图Fig.2 Sum rate vs.iteration number with different SNR

由图2可知，前6次迭代在高信噪比时随着迭代次数的增加系统的和速率逐渐增加，多于6次迭代后系统的和速率变化平缓。另从信噪比变化系统和速率与迭代次数的关系曲线可知，信噪比增大，信道环境较好时系统的和速率逐渐增大。从上述曲线可看出所提算法具有一定的收敛性。

6.2 MSE和性能分析

SNR=-5 dB、SNR=10 dB时不同预编码初始化方法下MSE和与迭代次数的关系如图3所示，其中QR分解初始化指的是本文所提出的初始化预编码矩阵方法，将其与随机矩阵初始化、右奇异矩阵初始化方法进行比较，此处迭代次数最大为40次。由图3可以看出，在高信噪比算法收敛时3种预编码矩阵初始化方法均具有较低的均方误差和，在低信噪比算法收敛时基于QR分解的初始化方法比随机矩阵初始化、右奇异矩阵初始化方法具有更低的均方误差和，这是由于所提算法在预编码矩阵初始化设计时充分考虑了干扰的影响所以具有更好的性能。

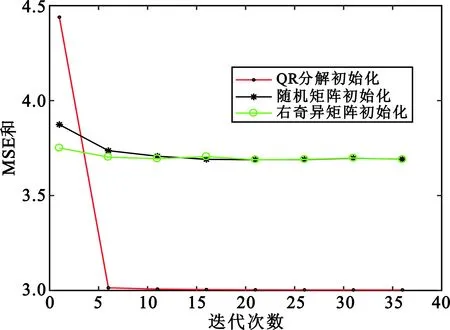
(a)SNR=-5 dB

(b)SNR=10 dB图3 不同预编码初始化方法下MSE和与迭代次数的关系Fig.3 Sum MSE vs.iteration number with different precoding initialization methods

6.3 不同算法和速率性能分析

最小干扰泄露算法、最大信干噪比算法、本文优化算法的和速率与信噪比的关系曲线如图4所示。

图4 不同算法和速率与信噪比的关系(15次迭代)Fig.4 Sum rate vs.SNR with different algorithms(15 iterations)

考虑到算法迭代15次时系统趋于稳定，所以3种算法在比较时迭代次数均设定为15次。由仿真结果可看出，随着信噪比的增加3种算法的和速率均增加，但本文优化算法性能要优于最小干扰泄露算法与最大信干噪比算法，最大信干噪比算法在中低信噪比时性能要优于最小干扰泄露算法，表明本文所提优化算法具有更好的系统性能。

6.4 不同算法的复杂度分析

最小均方误差(随机矩阵初始化)、最大信干噪比、最小干扰泄露及本文所提算法(QR分解初始化)的浮点操作数随迭代次数的变化关系如图5所示，可以看出4种算法中最大信干噪比算法的复杂度最高，本文所提算法复杂度次之，与最小均方误差算法复杂度相近，最小干扰泄露算法的复杂度稍低。4种算法总体复杂度相近，但本文所提算法具有更高的和速率性能，表明本文所提算法性能更优。

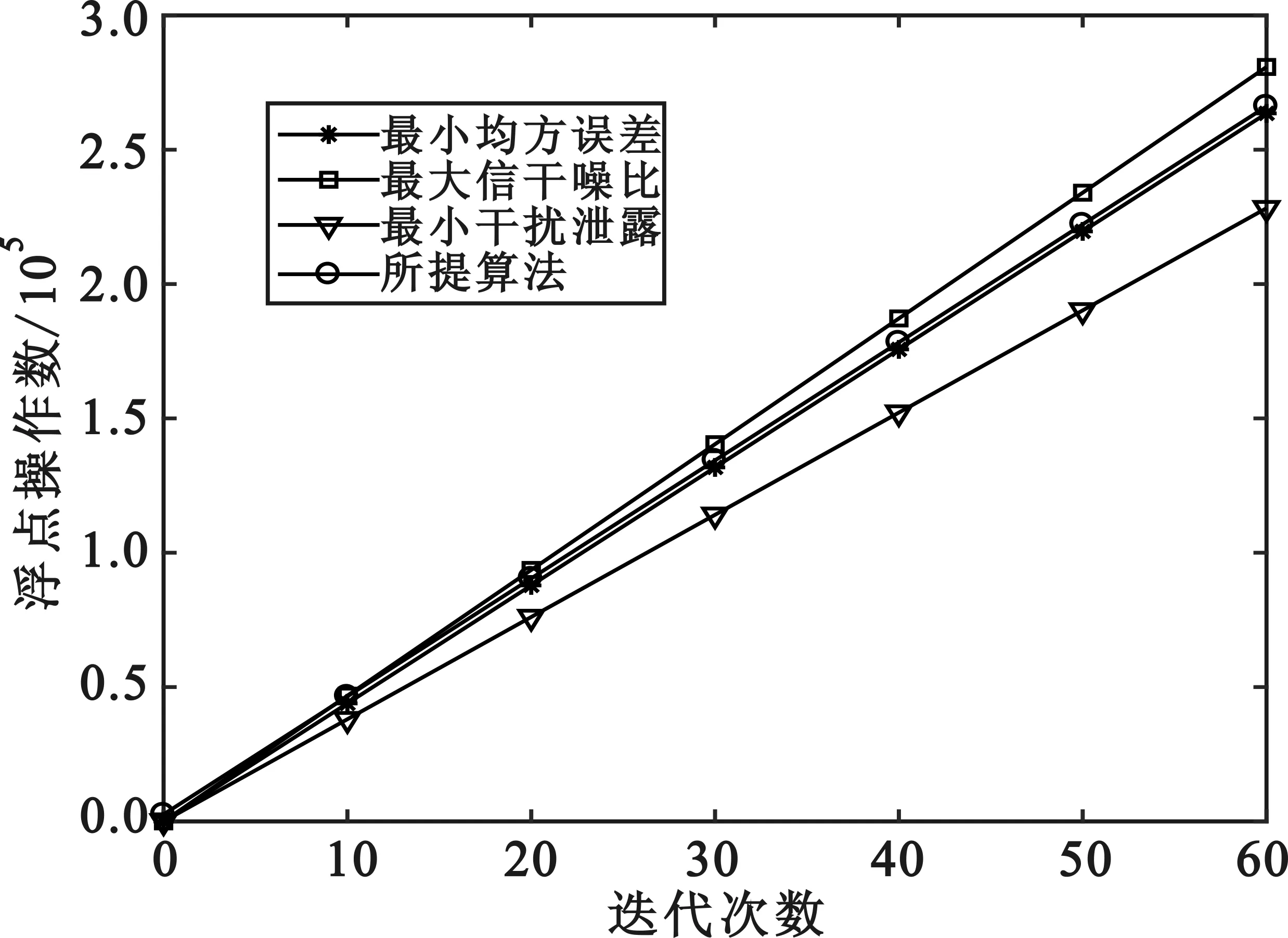
图5 不同算法复杂度分析Fig.5 Complexity analysis of different algorithms

7 结束语

本文在MIMO干扰信道中基于均方误差和最小化的优化标准提出了一种预编码矩阵初始化的新方法，该方法在设计预编码矩阵初始值时考虑了干扰的影响。理论分析和仿真结果表明本文所提算法具有一定收敛性，同时与其他算法的比较中可以看出本文所提算法具有更高的和速率，在低信噪比时具有更低的均方误差和。但本文在系统分析时信道状态信息是已知的，信道状态信息不完备的系统性能将作为今后进一步的研究方向。