空间目标的联合矩阵束极点估计*
邢煦然**a,赵宏钟,贾 鑫
(航天工程大学 a.研究生院;b.光电装备系,北京101416)
1 引 言
随着空间技术的发展,空间目标的雷达识别已经成为空间探测和感知领域的研究热点。雷达目标识别通过雷达电磁回波探测空间目标的尺寸、形状、轨道参数等重要属性,对空间目标进行分类,具有重要的民用和军事意义。当雷达信号的波长与目标的特征尺寸相当的时候,雷达回波会产生谐振现象。相当一部分空间目标尺寸处于远程监视雷达工作频段的谐振区,极点是雷达目标在谐振区的最主要特性。极点与目标相对姿态、雷达极化方式等无关,只与目标本身的大小、形状、材料等因素有关[1]。因此,极点可以克服光学区雷达目标识别存在的姿态敏感性,是一种稳健的目标识别途径。
从雷达回波中提取极点是谐振区目标识别的前提。经典的极点估计算法有Prony法[2]、矩阵束法和迭代法[3]。Prony法对噪声敏感并且有无法消除的病态问题,迭代法运算量大并且结果受初值选择的影响,而矩阵束法在运算量、精度和抗噪性等方面综合性能较优,因此运用最广[4]。在采用频域扫频观测数据提取目标极点时,存在虚假极点和真实极点遗漏的问题,其主要原因一是扫频数据截断导致时域信号泄露,二是模型定阶不准,三是单角度下某些真实极点的留数太小难以被提取。
针对上述问题,本文首先对目标频域数据进行加窗处理,并且对目标后时响应信号进行时域截断,有效地抑制了截断效应的影响;然后采用最小描述长度法(Minimum Description Length,MDL)估计出了目标信号的极点个数,避免了定阶错误引起的虚假极点;最后采用多角度联合矩阵束法估计目标的极点,有效减少了单角度下矩阵束法在估计极点时由于留数过小导致的虚假极点和极点遗漏,并分别采用简单细杆和空间卫星的高频电磁计算数据验证本文方法的有效性。
2 后时响应信号获取
2.1 奇点展开理论
1971年,Baum[5]在研究雷达回波的后时响应时首次提出了奇点展开理论(SEM)。SEM系统地描述了谐振区雷达目标的回波特性、传递函数以及性质。谐振区雷达目标的后时响应可以用极点的衰减复指数和表示:
(1)
式中:rm为留数;sm为极点,sm=σm+ωmj,σm为衰减因子,ωm为角频率;M为极点个数。目标的传递函数表述为有理函数和与整函数之和:
(2)
有理函数部分对应时域上的后时响应,整函数部分C(s)对应时域上的前时响应。上式变量中,留数ri和整函数项C(s)随观测角的变化而变化,而极点si具有姿态不变性。
2.2 频域数据的获取
谐振区雷达目标后时响应信号的获取方法有时域和频域两种:一是在时域直接用极窄脉冲的超宽带信号激励目标,采集目标回波;二是通过发射扫频或步进点频信号,获得目标在关心频带内的复频域响应H(ejω),再通过逆傅里叶变换获得目标的时域回波信号。时域测量方法存在超宽带激励信号产生复杂、回波采样率很高等问题,一般很少采用,因此本文采用后者。首采用CAD软件建立目标的3D模型,然后用网格剖分软件Hypermesh将模型表面的面元网格化,最后使用FEKO软件计算目标频域响应数据。此数据相当于使用一系列单点频信号激励目标时目标的频率响应H(ejω),对获得的频域数据逆傅里叶变换就得到目标的时域信号。本文的仿真目标分别选取了长度/半径200∶1的细杆和某型小卫星,如图1所示。
图1 细杆和小卫星网格Fig.1 The mesh and late-time signal of thin-cylinder and satellite
2.3 时域信号的预处理
传统的方法直接对频域数据进行逆傅里叶变换就得到目标的时域信号,这会带来两个问题:一是这样相当于用矩形窗进行频域截断,造成时域旁瓣能量泄露;二是由于IFFT周期效应,信号后期幅度会出现增长趋势,呈现出幅度两边大、中间小的现象,这与理论上后时响应信号衰减不符。这些问题不仅影响极点提取的准确性,而且会产生虚假极点。
针对旁瓣泄露问题,本文对频域数据加Hamming窗然后再做IFFT来抑制时域信号的旁瓣能量泄露。假设频域计算数据为H=[H(1)H(2) …H(N)]T,窗函数为W(n),目标的时域信号y=IFFT[W(n)Y(n)] 。
针对IFFT周期效应,对获得的时域信号在能量最低处截断。由于大部分能量集中在后时响应的前半部分,后半部分的极点留数很小可以忽略,这样做有利于选择主要极点,忽略虚假极点,并可以抑制IFFT周期效应造成的信号后期幅度增长。截断点的选择标准如下:对于时域信号y,选取一小段时长n,计算[y(m)y(m+1) …y(m+n-1)](m∈[1,(N-n)])的信号能量:
(4)
获得E=[E(1),E(2),…,E(N-n+1)],能量E最小的时间点就是截取的时间。改进后的后时响应信号获取流程如图2所示。
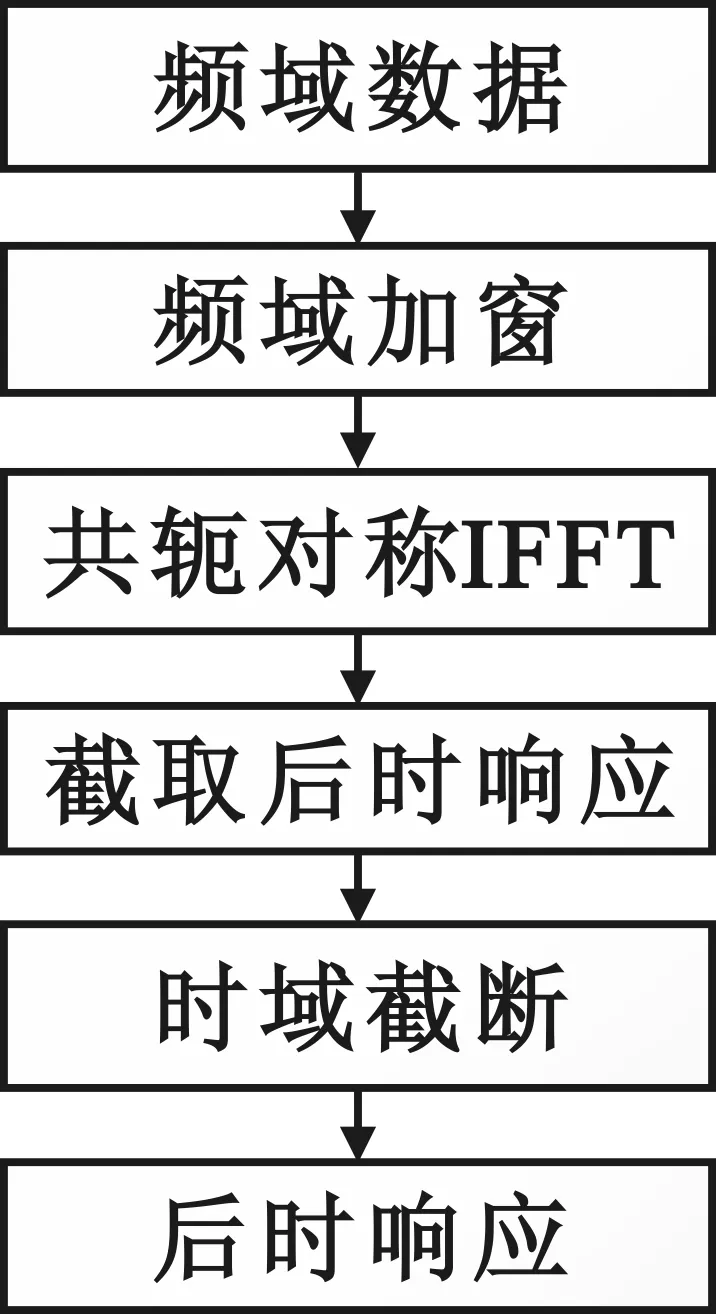
图2 获得后时响应流程图Fig.2 Technological process to obtain late-time response
3 联合矩阵束极点估计
矩阵束法求解极点的原理是将雷达目标在瞬态频率激励的谐振回波信号建模为S平面上的衰减指数和的形式,由此构造两个Hankel矩阵,利用Hankel矩阵特征值的之间特殊关系建立矩阵束,通过求解矩阵束的广义特征值,得到极点的估计。矩阵束法估计极点的流程包括以下五个环节:谐振区目标后时响应信号获取,极点个数的估计,Hankel矩阵构造,特征矩阵的构造,矩阵特征值求解。联合矩阵束与经典矩阵束法的区别在于Hankel矩阵是由多角度数据联合构造的。
3.1 极点个数估计
矩阵束法的求解过程需要对矩阵定阶,而阶数取决于回波信号中极点的个数,因此需要正确估计极点个数。本文选用MDL准则。文献[6]给出了MDL准则在极点估计问题的定义。
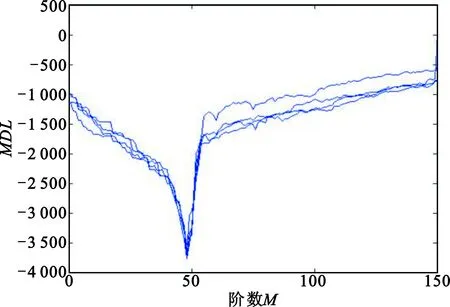
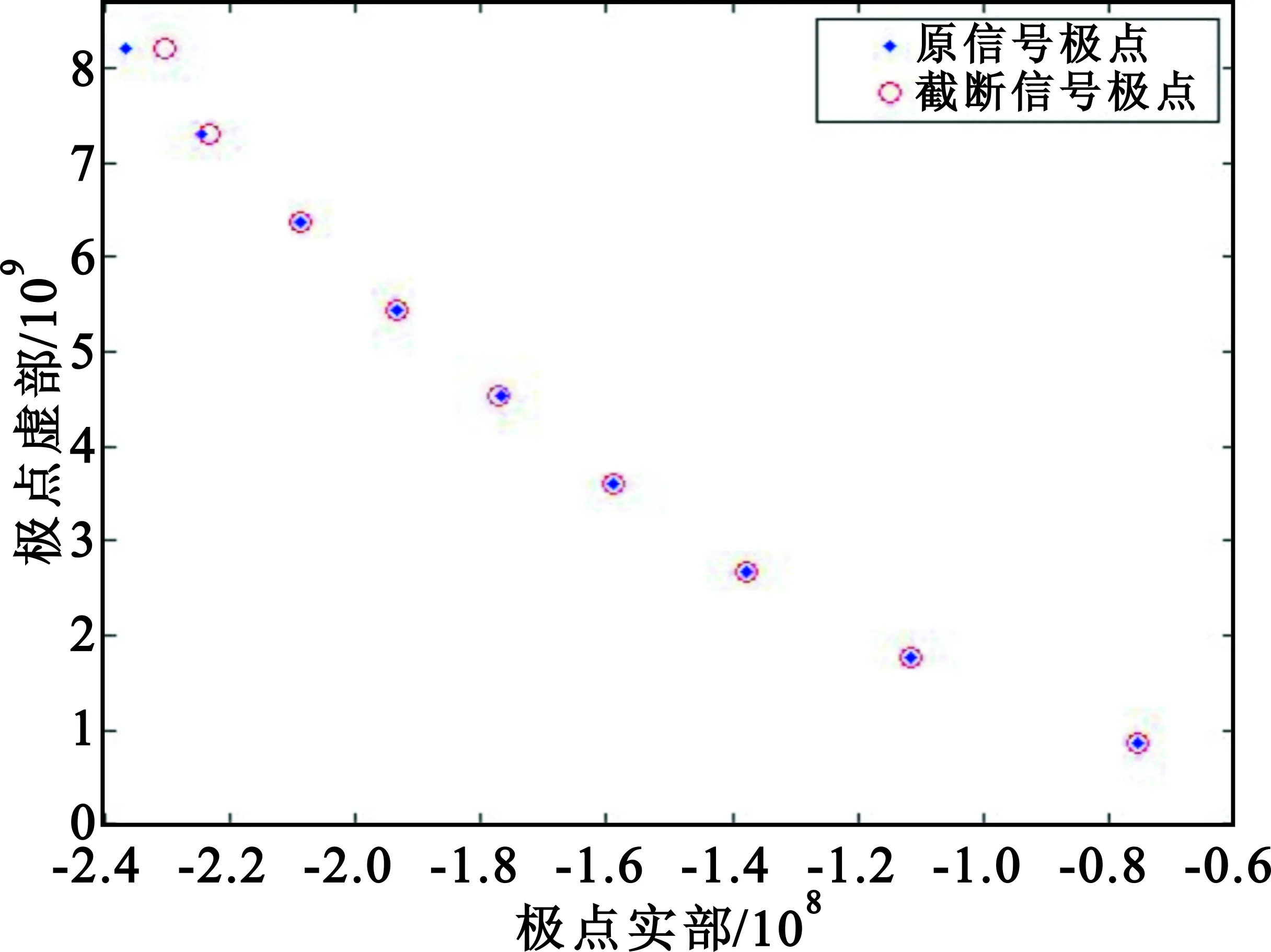
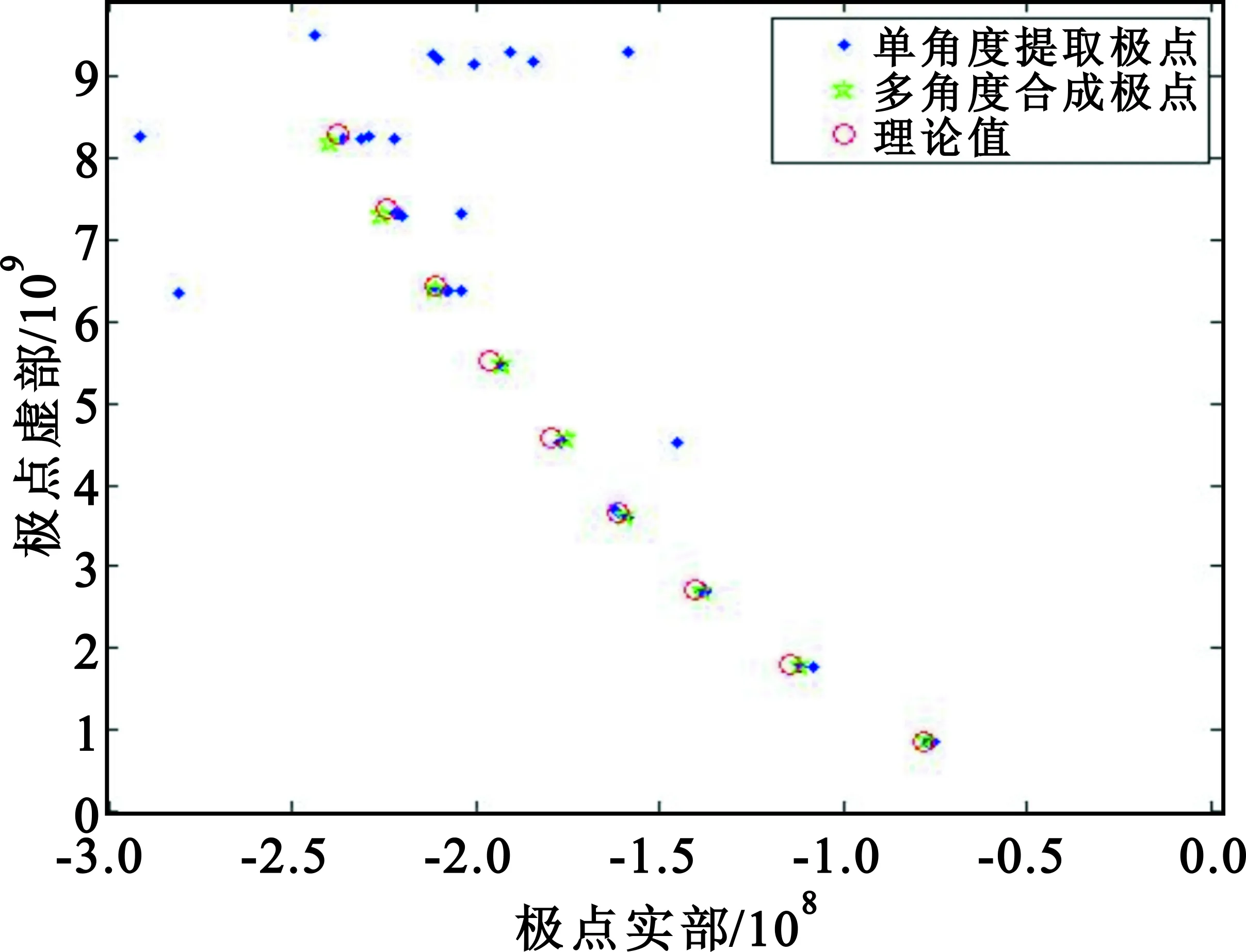
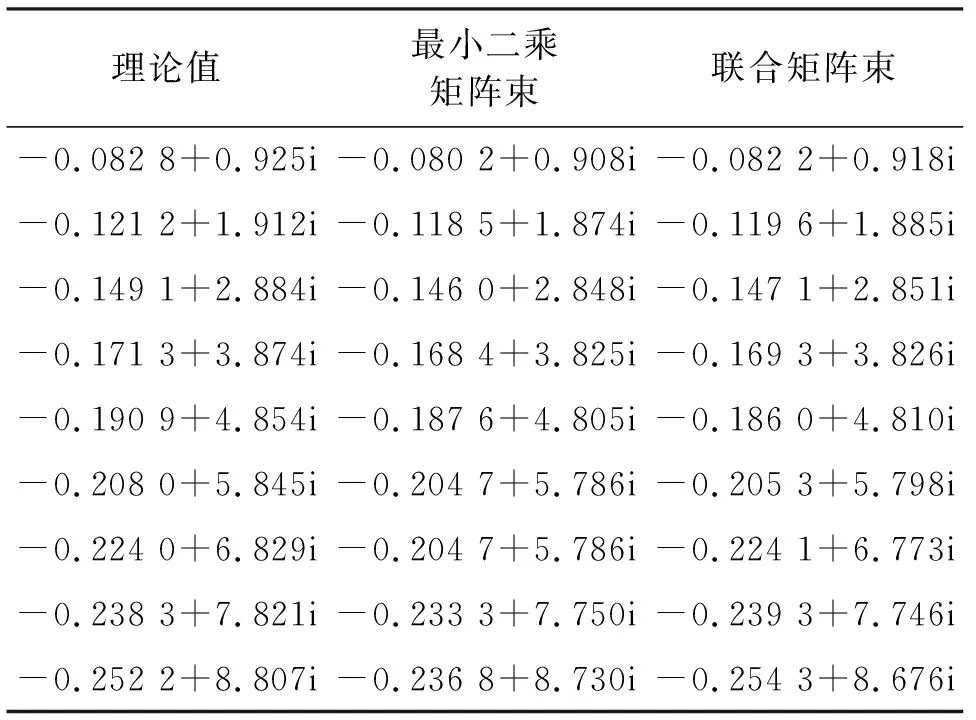
关于束参数的选取,研究表明束参数选取在N/3 极点本身具有姿态不敏感的特性,但是不同角度下观测的同一目标的后时响应时,极点对应的留数会随观测角变化而变化。留数的变化会导致在利用某个观测角度下的观测数据提取极点时,可能存在留数较小的现象。留数过小的极点被作为噪声无法提取,造成极点丢失;而同时奇异值更大的噪声却被作为极点而提取出来,成为虚假极点。为了解决留数变化造成的虚假极点问题,本文采用多角度后时响应信号构造联合矩阵,利用极点的姿态不敏感性可知,多角度观测联合矩阵在理论上具有相同的极点,因此联合矩阵的特征值与单一角度下的矩阵具有相同的特征值,通过对多角度联合矩阵奇异值分解,可以求得其广义特征值融合提取极点,不仅可以避免丢失重要极点,剔除虚假极点,还可以提高极点估计精度。 (1)单姿态下的Hankel矩阵构造 由式(2)获得目标的后时响应时域信号yi构造Hankel矩阵Yi: (5) 式中:i表示观测角度,i=1,2,…,K,K为总共获取的观测角度数。 (2)多角度下的Hankel矩阵构造 将各个角度下获得后时响应信号的Hankel矩阵横向排列: (6) (3)多角度矩阵束特征值求解 对式(6)中的联合矩阵D奇异值分解: D=USVT, (7) U、V分别为D的左奇异矩阵和右奇异矩阵。去掉V第一行和最后一行得到V1、V2,取U的前M列为U′,构造矩阵D1、D2: (8) (9) 本文算法流程可以概括如下: (1)由K个角度下的目标频域观测数据Hi获取时域响应数据,根据式(3)对频域数据做IFFT,计算获得时域信号每段的能量,在能量最小处对时域序列进行时域截断,获得各角度下的后时响应信号yi。 (2)构造多角度数据联合矩阵:由式(5)分别构造K个角度下的Hankel矩阵Yi,然后由式(6)构造多角度联合观测矩阵D。 联合矩阵束法与矩阵束法相比Hankel矩阵更大,因此其算法复杂度大于经典矩阵束法。最小二乘矩阵束法需要在不同极点个数下多次进行矩阵束,因此算法复杂度大于本文算法。算法复杂度从低到高排序依次为Prony法、矩阵束法、联合矩阵束法、最小二乘矩阵束法、迭代类算法。 采用高频电磁计算软件FEKO分别计算两个目标的验证算法:一是长和半径比200∶1的细杆目标,二是某小卫星。目标剖分模型见图 1 。使用FEKO计算细杆目标在方位角10°~90°范围内间隔10°,一共9个入射角度下,激励信号1~1.5 GHz的频率响应数据,以及某小卫星在7个入射角下激励信号0~1.5 GHz的频率响应。 根据极点的姿态不变性,理论上在不同的入射角下极点个数是相同的。用MDL法估计各个入射角下某小卫星后时响应的极点个数。图3列举了小卫星4个角度下的MDL曲线,可见各角度下最小值点的阶数一致,与理论相符。 图3 MDL随阶数变化曲线Fig.3 The MDL value- order curve 4.3.1频域加窗 加入了Hamming窗之后,信号的时域波形的旁瓣泄露问题会得到很好地抑制。频域加窗虽然会改变目标的时域波形,但不影响极点估计的准确性。图4给出了细杆加窗和不加窗的极点结果,与理论值比较,可以看出频域加窗后提取的精度更高。 图4 加窗对极点的影响Fig.4 Influence of windowing on poles 4.3.2时域截断 时域截断可以起到保留主极点、抑制虚假极点的作用。图5(a)对比了细杆时域截断前和时域截断后的极点,验证说明时域截断能保留主极点。由于简单几何目标虚假极点少,图5(b)对比了复杂目标某小卫星的时域截断效果,可以看出,时域截断后极点数量明显减少,但其分布特性一致。这些截断后消失的极点,都是一些小能量极点、虚假极点以及旁瓣泄露产生的不衰减的极点。可见时域截断对于进一步抑制旁瓣泄露的影响,保留主极点有明显的作用。 (a)时域截断保留主极点分布 (b)小卫星截断前后对比 4.4.1细杆的极点估计结果 联合矩阵束估计与经典矩阵束相比,可以克服单角度数据下的极点遗漏问题,并具有更强的抗噪性。图6(a)为60°入射角时,单角度下矩阵束的极点提取结果,是典型的极点遗漏情况;图6(b)为不加噪声时的多角度矩阵束合成结果;图6(c)为加入10 dB高斯白噪声下多角度联合矩阵束的提取结果。对比图6(a)与图6(b)可见,联合矩阵束算法克服了单角度下的极点遗漏问题。对比图6(c)中各个单角度下的极点结果与多角度联合矩阵束结果可以看出,联合矩阵束结果与理论值基本一致,有更高的抗噪性。 (a)单角度矩阵束的极点提取结果 (b)无噪声下的多角度联合估计结果 (c)10 dB噪声下的多角度联合估计结果 4.4.2复杂目标的极点估计结果 由于复杂目标无法获得其极点的理论分布,因此只将本文方法与单一角度下矩阵束的估计方法作为对比。将所有角度下的后时响应信号融合计算某小卫星的极点分布,结果如图7所示,可见多角度联合矩阵束估计算法可以获得有限的主要极点,同时滤出大部分的虚假极点。 图7 某小卫星的极点提取结果Fig.7 Pole extraction result of a small satellite 4.4.3与其他算法对比分析 以细杆为例,对比本文算法与最小二乘矩阵束法,结果如表1所示,可见与最小二乘矩阵相比本文算法精度更高。 表1 不同方法结果对比Tab.1 Comparison among different methods 本文研究了从雷达目标的频域扫频观测数据中估计复杂目标极点问题。通过频域加窗和时域截断相结合的方法预处理后时响应信号,抑制了旁瓣泄露。采用多角度联合矩阵束法有效减少了传统矩阵束法的虚假极点。分别用细杆和小卫星两种雷达目标电磁计算数据验证,结果表明,预处理有效降低了虚假极点的数量;联合矩阵束法克服了经典矩阵束法在单角度下的缺陷,具有更高的精度,并且在10 dB噪声下依旧适用。下一步的工作是目标建库和应用极点进行特征识别。3.2 联合矩阵特征值估计


4 仿真验证
4.1 仿真参数
4.2 极点个数估计
4.3 旁瓣泄露的抑制


4.4 极点估计结果



5 结 论

