稀疏重构混合源参数估计方法
王春霞 李丹阳 邓 科 殷勤业
(西安交通大学电子与信息工程学院,陕西西安 710049)
1 引言
信源定位是阵列信号处理的一个研究热点,在雷达、声呐、地质学、海洋学等方面都有重要应用。根据信号源与接收天线距离的不同,通常将信源分为近场源和远场源。近场源与天线阵列之间的距离r∈(0.62(D3/λ)1/2,2D2/λ)(D为阵列孔径,λ为信号波长);远场源与天线阵列之间的距离r≫2D2/λ。
源定位算法的研究起始于远场源,比较成熟的远场源参数估计算法有MUSIC算法和ESPRIT算法等。在近场源定位中,需要估计信源角度和信源距离两个参数,现有的近场源估计算法有二维MUSIC算法[1],高阶ESPRIT算法[2]以及广义ESPRIT算法[3]等。在某些实际应用中,如表面波雷达定位、基于麦克风阵列的说话人定位,以及室内自导引系统中,往往只有一部分信源位于阵列的近场区域,而另一部分信源位于阵列的远场区域。目前适用于远近场源共存的信源参数估计方法研究还不够充分,现有的混合源定位算法主要包括两阶段MUSIC算法[4]、斜投影 MUSIC算法[5]、基于子空间差分技术的混合源定位算法[6]等。两阶段MUSIC算法通过构造两个特殊的高阶累积量矩阵来解决源分离问题,计算量大,且当远近场源存在相近角度时会出现估计错误。斜投影 MUSIC算法采用斜投影算法分离出近场源信息并构建新的协方差矩阵,但由于仅利用了新的协方差矩阵的斜对角元素信息,估计精度有所下降。基于子空间差分技术的混合源定位算法在获得远场角度的基础上,通过差分技术获得抑制噪声后的近场协方差矩阵,实现了近远场源的有效分离。以上三种都是子空间类算法,这类方法受子空间理论框架的限制,在信噪比较低、阵列快拍数不足或出现相干信号源的情况下,参数估计性能会急剧下降,甚至失效。
近年来,随着压缩感知理论体系的出现和不断完善,作为其核心的稀疏重构框架被引入阵列信号处理,出现了许多基于稀疏重构的信源参数估计算法,如Wang等人提出的稀疏混合源定位算法[7]、l1-SVD[8]算法、JLZA-DOA[9]算法、文献[10]提出的稀疏近场源定位算法以及一类为了解决稀疏重构条件下的网格失配问题而提出的算法[11-15]等。文献[7]提出的基于高阶累积量的稀疏混合源定位算法借助稀疏信号重构获得了更好的分辨率和估计精度,突破了子空间类算法的局限性,其构造的矩阵大小为(2M+1)×(2M+1)2(L=2M+1,L为阵元个数),但并未使用全部的累积量矩阵信息,所利用的有效元素个数与本文算法构造的(2M+1)×(2M+1)维的矩阵相当。文献[7]在进行近场距离估计时,将远场源当作特殊的近场源处理,在估计近场距离时也需对远场距离进行估计,算法效率严重下降。文献[10]使用了稀疏重构思想对近场源参数进行估计,利用了二阶累积量方法,但其在估计近场源DOA时,仅使用了接收信号自相关矩阵(2M+1)2个元素中的(2M+1)个,信息利用率低,在一定程度上制约了算法的估计精度。
本文提出的基于稀疏重构的混合源参数估计算法利用二阶统计量来进行参数估计,采用l1-SVD算法的改进形式结合稀疏重构思想估计出远场到达角,由估计出的远场角度和远场源信号功率对远场协方差矩阵进行重建,再从信号协方差矩阵中减去重建的远场协方差矩阵得到近场协方差矩阵的估计,接着利用旋转不变思想构造目标函数,通过对目标函数求最优解得到近场源到达角,最后利用估计出的到达角对近场阵列流形进行稀疏重构,得到近场源的距离估计。
2 混合源信号模型
如图1所示,假设共有K个窄带独立信源入射到由L=2M+1个阵元组成的均匀等距线阵上。不失一般性,假设前K1个信号源为近场信号源,后K-K1个为远场信号源。
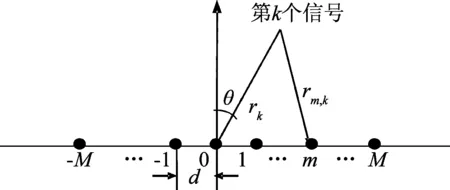
图1 混合源模型Fig.1 The mixed sources model
以阵列中心为相位参考点,则第l个阵元在t时刻的接收信号可表示为:
(1)
其中sk(t)表示第k个窄带信源,nl(t)表示该阵元上的加性噪声,τlk表示第k个信源从0阵元到l阵元的延迟相位。对于第k个近场源,τlk为:

(2)


(3)
式(1)可以用矩阵形式表示为:
x(t)=ANsN(t)+AFsF(t)+n(t)
(4)
式中
x(t)=[x-M(t),…,xM(t)]T
(5)

(6)

(7)
sN(t)=[s1(t),…,sK1(t)]T
(8)
sF(t)=[sK1+1(t),…,sK(t)]T
(9)
n(t)=[n-M(t),…,nM(t)]T
(10)

3 远场源到达角估计
首先对远场源到达角进行估计,由阵列的接收矢量x(t)构造阵列的协方差矩阵R:
R=E{x(t)x(t)H}=RN+RF+σ2I
(11)
式中E{·}表示取期望,[·]H表示共轭转置,RN和RF分别为远场和近场协方差矩阵,σ2为噪声功率,I为单位矩阵。
假设信源总数K已知。利用文献[16]的思想,将远场源所在角度区域划分网格并形成集合Θ=[θ1,θ2,…,θN0],其中N0是划分的网格数,且N0满足N0≫K,则协方差矩阵可以稀疏表示为:
R=A(Θ)S+ANSN+N
(12)
其中A(Θ)=[a(θ1),…,a(θN0)]表示过完备的远场阵列流形矩阵,S为N0×L维的稀疏矩阵。当网格划分足够密集时,会有(K-K1)个角度θ={θK1+1,θK1+2,…,θK}∈Θ或者在Θ中有对应的近似值。式(12)的过完备表示将到达角的估计问题转换成了求解S的新问题,通常信源在某一范围内个数很少,S对应的谱是稀疏的,符合稀疏重构所需要满足的信号稀疏性。
基于上述分析,结合对R的稀疏表示,构造如下的目标函数:
(13)
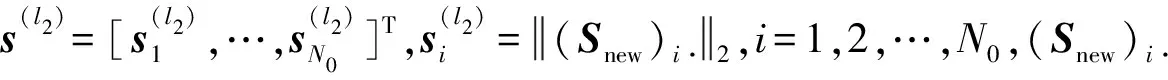
4 近场源参数估计
4.1 近远场协方差分离
在得到远场源到达角的估计之后,根据式(11)可得RN=R-RF-σ2I,因此可以通过估计RF和σ2来得到RN的估计[6]。对R进行特征值分解:
(14)
其中Δs为大特征值构成的对角阵,Us为对应特征向量构成的信号子空间,Δn为小特征值构成的对角阵,Un为对应特征向量构成的噪声子空间。
结合(11)和(14)两式得到:
(15)
RF可以通过下式进行估计:
(16)
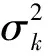
(17)
[·]†表示伪逆。
RN可以表示为:
(18)
其中σ2为噪声功率,通过对R的(L-K)个小的特征值求平均可以得到其估计值。由式(18)可以看出,从信号协方差矩阵中既消除了阵列噪声,又消除了远场源信息,可以更好地实现混合信号的抑噪和分离。
4.2 近场源到达角估计
为避免二维搜索,提高估计精度,利用均匀线阵的对称性对近场源方向矩阵AN进行分块处理:
(19)
其中

(20)

(21)


(22)
等式(21)可以进一步表示为:

(23)
现在使用稀疏重构来估计近场源到达角,对RN进行特征值分解:
(24)

对Gs进行分块处理:
(25)


(26)

(27)
结合上述分析,构造如下的目标函数:
(28)

4.3 近场源距离的估计
(29)

根据稀疏重构理论,近场源距离的估计问题可以表示为如下的l1范数最小化目标函数:
(30)
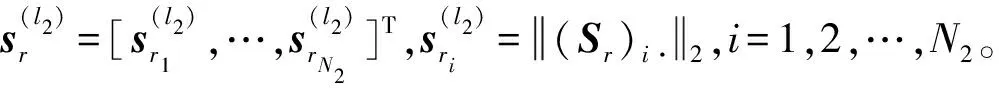
本文算法的具体步骤如下:
1)获得协方差矩阵R,通过求解式(13)的优化问题,得到远场源的角度估计值;
2)由得到的远场源角度估计值重构远场协方差矩阵RF,利用子空间差分方法得到RN;

4)根据得到的近场源角度估计值,求解式(30)得到近场源距离的估计值。
5 计算复杂度
关于计算复杂度,这里主要考虑累积量矩阵的构建、特征值分解、稀疏重构等主要过程。本文算法需两次(2M+1)×(2M+1)维的特征值分解和三次稀疏重构过程。在混合源参数估计中,文献[7]需要构建(2M+1)×(2M+1)2维的累积量矩阵,(2M+1)×(2M+1)2维和(2M+1)×N维两个矩阵的SVD分解,两次稀疏重构过程。对比可知,由于构建了高阶累积量矩阵,文献[7]比本文算法具有更高的计算复杂度。文献[6]仅需两次特征值分解和三次谱峰搜索,其复杂度低于本文算法, 但本文算法的参数估计效果优于文献[6]。具体的运算量如表1所示,其中N为快拍数,N0~N3分别为远场角度域、近场角度域、远场距离域和近场距离域划分的网格数。将本文算法与文献[6]、[7]进行比较,考虑两个远场源位于(-5°,)和(30°,),两个近场源位于(-5°,3λ)和(20°,4λ),快拍数为500,信噪比为10 dB,对每种算法运行100次仿真实验并获得平均运行时间,结果如表2所示。可以看出,采用MUSIC类谱峰搜索的文献[6]运算时间最短,本文算法次之,文献[7]基于高阶累积量的稀疏重构算法运行时间最长,这正好和三种算法的计算复杂度相对应。

表1 计算复杂度比较

表2 平均运行时间
6 仿真结果及分析
实验采用11个阵元组成的均匀线阵,阵元间距为0.25λ,信源为等功率的互相独立的窄带信源,噪声为复加性高斯白噪声,且信源与噪声互不相关。实验2和实验3的仿真结果基于500次独立的蒙特卡罗试验。
信噪比(SNR)和均方根误差(RMSE)分别被定义为:
(31)
(32)

实验1验证本文算法的角度分辨能力及估计信源个数的能力,对比算法选择文献[6]。首先考虑有相同混合源到达角的情况,假设空间中有三个远场源位于(-15°,),(-5°,)和(20°,),两个近场源位于(-30°,1.8λ)和(10°,2.2λ),快拍数N=2000,信噪比SNR=10 dB。从图2和图3可以看出,当信源个数较多时,文献[6]中的算法已无法对近场角度和近场距离做出正确估计,而本文算法依然保持着非常尖锐的谱峰。因此,本文算法在信源个数较多情况下的估计效果远远优于文献[6]中的算法。
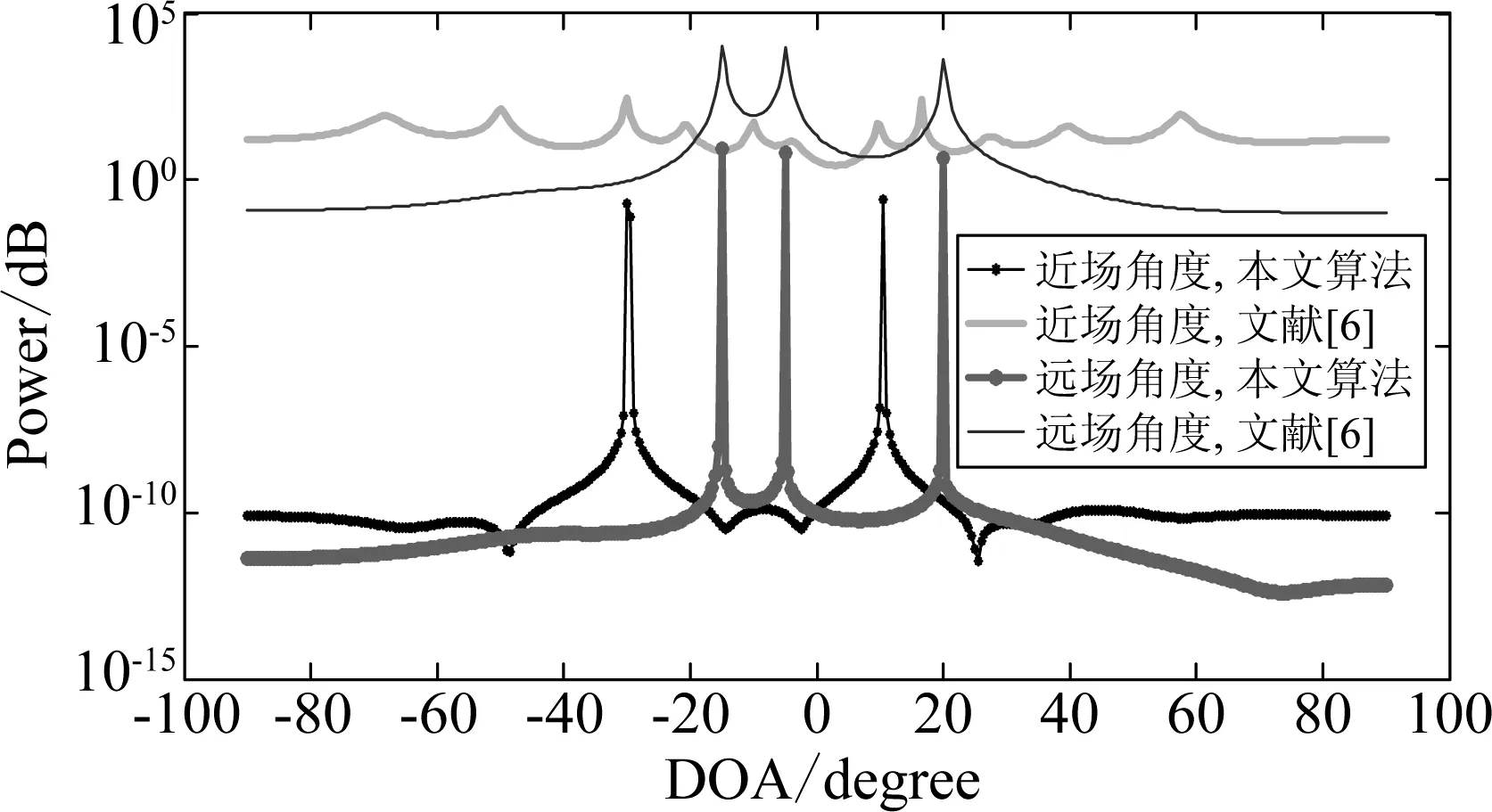
图2 混合源角度估计谱Fig.2 The estimated spatial spectrums of mixed sources

图3 近场源距离估计谱Fig.3 The estimated range spectrums of near-field sources
为了更好地说明本文算法相比于文献[6]方法的高分辨率,令信噪比从0 dB变到30 dB,每种信噪比条件下进行1000次重复实验,其余仿真条件不变,绘制出远场信源的分辨概率随信噪比变化的情况,如图4所示。从图4可以看出,本文算法空间分辨概率在0~10 dB之间随着信噪比增加几乎直线上升到最大概率,并一直维持在最大概率。而文献[6]中基于谱峰搜索的算法的空间分辨概率在0~10 dB之间概率为0,10~15 dB稍微有所上升,15~20 dB才开始有明显上升,后缓慢上升至最大概率。因此本文算法的空间分辨率明显优于文献[6]中的方法,这也验证了稀疏重构的高分辨率特性。

图4 远场源分辨概率变化曲线Fig.4 The resolutions versus SNRs for far-field sources
实验2仿真混合信源下本文算法的估计效果,对比算法选择文献[6]。假设空间中两个远场源分别位于(-5°,),(30°,),两个近场源分别位于(-15°,3λ),(20°,4λ),信噪比从-10 dB变到15 dB,快拍数为500。从图5可以看出,无论是近场源还是远场源参数估计,本文算法的估计精度均优于文献[6]。

图5 混合源均方根误差随信噪比变化曲线 Fig.5 RMSEs of mixed sources versus SNRs
实验3为纯近场信源参数估计性能的仿真,对比算法选择文献[6]、[7]和[10]。假定两个近场源位于(-5°,3λ)和(20°,4λ),其他参数同实验2。观察图6结果可以看出,本文算法在近场到达角估计中具有更低的估计误差,估计精度明显优于其他两种算法。在距离估计中,当信噪比较低时,本文算法与文献[10]估计精度相当,并高于文献[6]和[7],而在高信噪比下,本文方法和文献[6]效果趋于一致。文献[7]算法由于高阶累积量在高信噪比下优异的噪声鲁棒性,具有最佳的近场距离估计效果,但其未分离近场源和远场源,在近场距离估计时,也要将远场信源当作特殊的近场源进行距离估计,复杂度高于本文算法。

图6 纯近场均方根误差随信噪比变化曲线Fig.6 The RMSEs of DOAs and ranges versus SNRs of pure near-field sources
7 结论
本文提出了一种基于稀疏信号重构的混合源分离定位方法。首先使用l1-SVD算法的改进形式估计出远场源到达角,然后采用协方差差分方法得到近场源协方差矩阵,再通过对近场源协方差矩阵稀疏重构估计出近场源到达角,最后利用估计出的近场角度对近场源协方差矩阵进行稀疏表示,估计出近场源距离。本文方法在充分利用二阶统计量信息的同时,不必进行二维谱峰搜索和额外的近场源参数配对,同时避免了构造计算复杂度高的高阶累积量矩阵。仿真结果验证了本文算法的有效性和空间分辨能力,与文献[6]中基于MUSIC的算法相比,本文算法估计精度高,具有更好的混合源分离效果和空间分辨率,避免了文献[6]中由于近场距离谱峰不明显而可能导致的估计失败问题;与文献[7]相比,本文算法避免了高阶累积量的构建,也不需要对远场距离加以估计,有效降低了运算量;与文献[10]相比,本文算法利用了所有阵列接收自相关矩阵元素的信息,较高的信息利用率保证了更优的信源参数估计精度。在纯近场条件下,本文算法具有更高的角度估计精度,且低信噪比条件下的近场距离估计精度也很高。

