菱形中继网络中基于叠加训练的信道估计技术研究
邓 冉 高 俊 何宪文
(海军工程大学电子工程学院, 湖北武汉 430033)
1 引言
菱形中继网络通过灵活设计传输协议,利用分布在空间不同位置的用户天线来构造虚拟多天线阵列[1],能够有效获取分级增益对抗多径衰落[2],实现类似MIMO(Multiple-Input-Multiple-Output)的空间分集效果[3]。随着微蜂窝技术在5G通信网络中的应用,小区范围不断缩小,菱形中继网络具有中继节点发射功率小、部署灵活等特点,非常适合应用于5G网络。对于目前广泛采用的AF模式,在许多应用场景,如分集合并、最佳功率分配、最佳中继选择,分布式空时编码等[4- 6]都要求需要在获取级联信道的信道状态信息(CSI)的同时估计单跳信道,涉及到多个(级联或单跳)信道分离估计问题,带来的多训练序列优化问题更加复杂[7]。
在AF模式下的中继协作网络中关于信道估计的研究最早主要集中在级联信估计方面,文献[8]中设计了一种循环正交训练,文献[9]中,推导了MIMO系统中继放大矩阵设计的必要条件。然而,文献[8]和[9]中忽略了单跳信道估计对于系统优化的重要性[10-11]。文献[12]研究了一种多用户接收机,可以对中继链路各单跳信道进行盲估计,但是很难通过盲方法获取即时的CSI。文献[13]提出一种带内叠加训练进行单跳信道估计,通过将中继训练序列直接叠加到数据序列上,使得单跳信道和级联信道相互独立地进行,且消除了协作干扰和中继传输噪声的影响,但是由于在中继进行了干扰置零,以信号失真为代价获得信道估计的提升,降低了端节点符号检测性能。文献[14]提出时分叠加训练方案,在中继节点将自身训练叠加到源训练符号上,通过优化训练序列设计实现级联和单跳的分离估计。
本文针对单载波频域均衡系统,为了节省带宽的同时获取单跳信道的CSI,将时分叠加训练的帧结构设计思想拓展到菱形中继网络,开展高效信道分离估计理论研究。提出了一种适用于AF菱形中继网络的基于叠加训练(ST)信道估计方案,以消除多址接入干扰和训练间互干扰为目标,进行最优的多训练序列设计。新方案将中继训练叠加到源训练序列上,通过对中继识别符号以及中继训练组进行联合优化设计,设计了一种基于频域循环移位的正交扩展序列组生成算法;并且提出了一种中继噪声消除算法有效地解决了非高斯复合噪声对单跳信道估计的性能恶化问题。通过仿真实验,探究了最佳中继功率分配,并且分析验证了方案的有效性。
2 系统模型
以菱形中继协作为系统模型,如图1所示,包括源节点S,两个中继节点R1和R2以及目的节点D。
源节点S与目的节点D的通信分为两个时隙,在第一时隙内,源节点S分别向中继R1和R2广播数据;在第二时隙内,两中继放大接收数据并且转发至目的节点D,从而得到两份独立衰落的信息副本。

图1 菱形中继网络结构框架Fig.1 Diagram for cooperative diversity of diamond relay network
假设菱形中继网络中,所有节点均只配备一根天线,工作在半双工模式下。在该中继网络模型中,S到R1的信道(S→R1)、S到R2的信道(S→R2)、R1到D的信道(R1→D)以及R2到D的信道(R2→D)冲激响应分别表示为
hSR1=[hSR1(0),hSR1(1),…,hSR1(LSR1-1)]T
hSR2=[hSR2(0),hSR2(1),…,hSR2(LSR2-1)]T
hR1D=[hR1D(0),hR1D(1),…,hR1D(LR1D-1)]T
hR2D=[hR2D(0),hR2D(1),…,hR2D(LR2D-1)]T
(1)
其中LSR1、LSR2、LR1D以及LR2D为对应的信道阶数,其他各项参数做如下假定:
1)信息符号d(n)为相互独立均匀分布的随机变量,取自调制信号符号集,均值E{d(n)}=0,符号功率进行归一化,即E{|d(n)|2}=1。
2)中继和目的节点噪声均为独立同分布的加性高斯白噪声(Additive White Gaussian Noise, AWGN)。
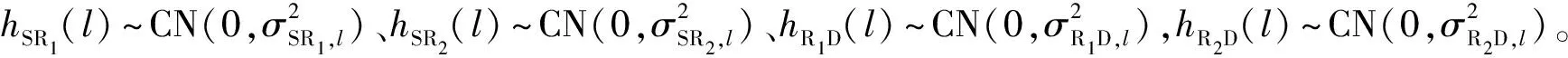
4)数据帧由一个训练块和一个信息块组成。
源节点训练序列和信息序列分别用tS=[tS(0),tS(1),…,tS(N-1)]T∈CN×1和d=[d(0),d(1),…,d(N-1)]T∈CN×1表示(本文为了方便描述,训练块长度Nt和信息块长度Nd都用N表述)。时分叠加训练的帧结构如图2所示。
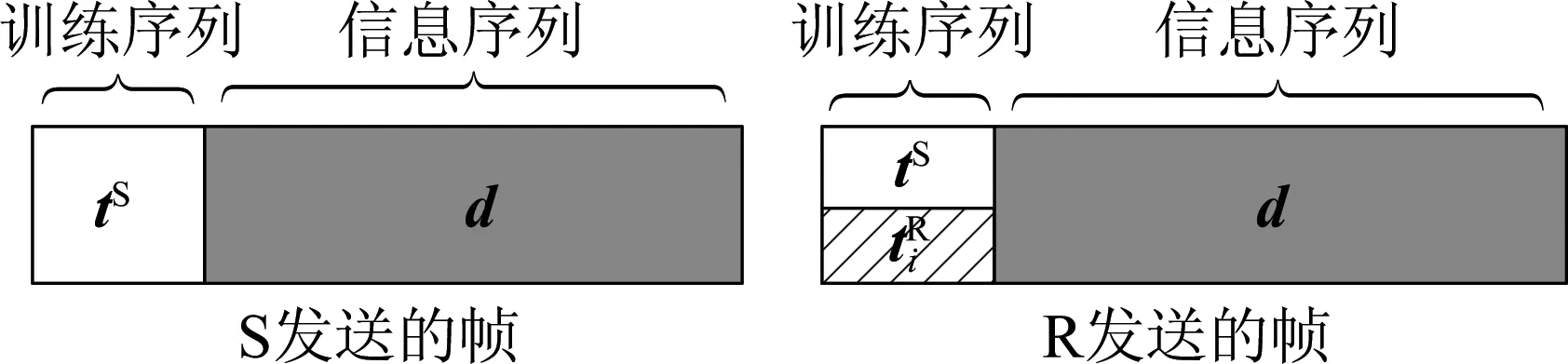
图2 时分叠加训练方案的帧结构图Fig.2 Frame structure with relay superimposed training scheme
为了消除块间干扰(Inter-Block Interference, IBI),通过插入和去除合适长度的循环前缀(Cyclic Prefix, CP)进行传输。不失一般性地,源节点会用全部功率Ps发送数据帧,训练序列和信息序列的平均发射功率分别为(tS)HtS/N=Ps和E{dHd}/N=Ps。
(2)
(3)
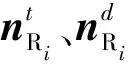
在第二时隙,R1和R2中继分别对接收的数据进行放大转发,由于目的节点不具备识别不同中继对应信道的能力,因此在中继对训练块增加不同的识别符号后叠加中继训练序列,中继处理后的训练序列和信息序列可以表示为:
(4)
(5)

(6)
(7)
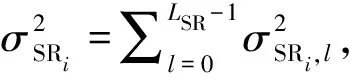
在第二时隙,在目的节点接收的训练序列和信息序列分别为:
(8)
(9)
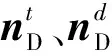
3 信道估计
为了实现分集合并,需要获得中继链路各单跳信道的CSI,根据式(8),在目的节点接收的训练序列可以表示为:
(10)
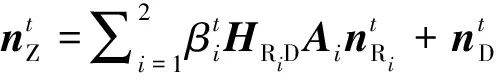
(11)

(12)
为了使得R1→D单跳信道估计的MSE最小,需要满足下列条件:
(13)
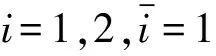
(14)

(15)
为了使得S→R1单跳信道估计的MSE最小,需要满足下列条件:
(16)
对应地,同时考虑以R2中继链路为研究对象后,可以将上述条件,转换为一般性的条件表述:
(17)
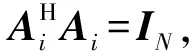

图3 训练序列的频域结构Fig.3 Sketch for structure in frequency domain for training sequence

tS(l)=ejπl(l+υ)/P,Pis oddυ=1,Pis evenυ=2
(18)
A1=Π1
A2=Π3
(19)
其中P为训练序列的周期。
对应的Ri→D单跳信道LS估计的MSE可以表示为:
(20)
根据条件C2,最小的MSE可以进一步表示为:
(21)
根据式(21)可以判断,对中继识别矩阵以及不同的中继训练序列优化后,Ri→D单跳信道的估计性能仅与非高斯复合噪声有关,能够消除多址接入干扰以及源训练与中继训练序列间的干扰。然而S→Ri单跳信道的估计性不仅仅与非高斯复合噪声有关,同时还受到Ri→D单跳信道的估计误差的影响。
4 中继消噪算法
根据式(21),中继引入的噪声在中继被放大,在接收端的非高斯复合噪声实际上是本地噪声与中继传输噪声的混叠噪声,且后者恶化了单跳信道的估计性能。因此,为了消除单跳信道估计过程中前一级信道累计噪声的影响,设计了一种中继消噪算法。考虑到源训练序列与中继训练序列相互正交,频域离散且占据不同的频点的特点,对中继接收信号进行预处理,消除中继接收信号特定位置的频域幅值,用以容纳中继训练,从而消除中继传输噪声对信道估计造成的影响。

(22)
(23)

(24)
采用中继消噪算法后,单跳信道的最小MSE可以进一步表示为:
(25)
5 符号检测
(26)
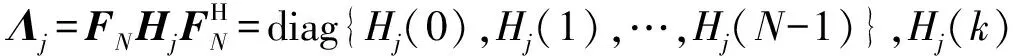
(27)


(28)
6 仿真实验与分析
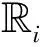

图4 时分叠加训练方案中不同信噪比下功率比与MSE曲线Fig.4 MSE versus power allocation ratio at different SNR conditions with relay superimposed training scheme
可以明显发现,在时分叠加训练方案中,随着中继训练功率比γ增加,源训练序列功率减小,中继训练序列功率增大,Ri→D单跳信道的估计性能增加,而S→Ri单跳信道不仅受中继节点分配的功率影响,还与Ri→D单跳信道的估计性能息息相关,因此一开始由于Ri→D单跳信道的估计性能提高,S→Ri单跳信道估计性能随之提高,之后受功率因素的影响更为严重,因此S→Ri单跳信道估计性能随之下降,在0.4≤γ≤0.7之间保持稳定,获得最佳的信道估计性能。
由于γ与SER之间存在复杂的数学关系,在理论上获得最优的功率分配因子γ是极为困难的,本节采用仿真的方法探究不同功率分配因子下的SER性能。在时分叠加训练方案中,随着中继训练功率比γ增加,信息序列的在中继节点的发射功率不变,因此,与信道估计性能相对地,如图5所示,符号检测性能SER曲线大约在0.4≤γ≤0.7较大区域内相对平坦,最佳的功率分配因子存在平坦区域内。假设时分叠加训练的中继训练分配因子分别取γ=0.4,各单跳链路的信道估计性能MSE、符号检测性能SER分别与协作中继网络SNR的关系如图6和图7所示。

图5 时分叠加训练方案中不同信噪比下功率比与SER曲线Fig.5 SER versus power allocation ratio at different SNR conditions with relay superimposed training scheme

图6 信道估计均方误差与信噪比曲线Fig.6 The curves of MSE versus SNR for channel estimation
可以明显发现,如图6所示,在时分叠加训练方案中,Ri→D单跳信道的估计性能较S→Ri单跳信道更好,根据式(21),未采用中继消噪算法的Ri→D单跳信道仅受包含中继传输噪声在内的非高斯复合噪声的影响,而S→Ri单跳信道还与Ri→D单跳信道估计误差相关;而采用中继消噪算法后,Ri→D单跳信道的估计性能提高明显,消除了中继传播噪声的影响,仅与目的节点引入的白噪声相关,即消除了非高斯复合噪声,有效地提高了估计性能;对应地其S→Ri单跳信道估计性能也相应的得到提高。
如图7所示,比较了本文中提出的基于时分叠加训练的信道估计方案以及文献[13]中的带内叠加训练方案的符号检测性能,在带内叠加训练方案中,其本质是将中继训练序列叠加到接收的信号上,以部分失真为代价换取较好的信道估计性能。由于中继干扰置零操作引入了严重的信息失真,检测性能经过1次迭代后提高效果明显,2次迭代后性能不再随之提高,是由于文献[13]迭代重构算法依赖于初始的检测性能,所以其补偿能力有限。对应地,本文提出的方案由于不存在信息失真,其符号检测性能明显高于带内叠加训练方案。相比时分叠加训练方案理想CSI下的检测性能,可以明显判断,信息失真导致了部分的性能损失,且该部分性能损失为迭代重构不能修复的性能损失。因此本文提出的时分叠加训练能够在不引入失真的情况下获得高性能的信道估计,且应用环境更加丰富。
7 结论
为了节省带宽的同时获取单跳信道的CSI,将时分叠加训练的帧结构设计思想拓展到菱形中继网络,开展高效信道分离估计理论研究。提出了一种适用于AF菱形中继网络的基于ST的单跳信道估计方案,以消除多址接入干扰和训练间互干扰为目标,进行最优的多训练序列设计。通过仿真实验,探究了最佳中继功率分配,验证了中继消噪算法能够完全消除非高斯复合噪声对单跳信道估计性能恶化,有效地提高了估计性能。对比同类型的信道估计方案,本文提出的方案能够不引入信息失真,获得更好的符号检测性能。

