一种自适应阈值选择的宽带压缩频谱感知重构算法
刘 洋 任清华,2 孟庆微 徐兵政
(1. 空军工程大学信息与导航学院,陕西西安 710077;2. 中国电子科技集团航天信息应用技术重点实验室,河北石家庄 050081)
1 引言
随着信息技术的不断发展,庞大的数据和信息量对信号带宽的要求越来越高,认知无线电基于传统奈奎斯特采样定律的宽带频谱感知技术使硬件设备越来越难以承受因高速采样而带来的载荷,针对这一问题,基于压缩感知[1-2](Compressed Sensing,CS)理论的认知无线电宽带频谱感知技术,即宽带压缩频谱感知,已成为解决宽带信号采样、压缩与恢复问题新的思路和重要手段,于此同时,宽带压缩频谱感知重构算法在恢复信号时很难获取信号的先验知识,因此,对重构算法进行盲稀疏度研究改进对于认知无线电宽带压缩频谱感知而言显得尤为重要。
目前,基于压缩感知理论的宽带频谱感知技术已成为研究热点。Tian等[3]首先提出并验证了宽带压缩频谱感知的有效性;之后Tian等[4]又提出了一种基于循环检测的宽带压缩频谱感知算法;文献[5]提出了一种调制宽带转换器(Modulated Wideband Converter,MWC)采样方法,能够以远低于奈奎斯特采样率对宽带信号进行采样;文献[6]利用压缩感知中的重构算法对压缩后的测量数据进行信号恢复,得到信号的功率谱实现宽带频谱感知。然而,以上算法都需要已知信号稀疏度作为先验知识。文献[7]通过模拟仿真实验完成了对频谱稀疏度的估计,但是必须重构出原始信号才能完成频谱估计,且对频谱稀疏度估计的理论分析不足;文献[8]利用随机矩阵理论分析待测信号协方差矩阵的特征值对稀疏度进行估计,但是该方法应用的前提是频谱具有明显的稀疏性,当主用户占用大量子信道时,该方法性能不理想;文献[9]针对频谱非稀疏的情况,通过引入导频信号实现对频谱的估计,然而主用户的信噪比在一定程度上会受导频信号的影响。
重构算法作为压缩感知理论的关键技术,其性能直接影响宽带压缩频谱感知的结果,其中贪婪算法由于结构简单、运算量小以及重构精度高等特点而广泛应用于宽带频谱感知的问题中。针对贪婪算法在未知信号稀疏度、环境噪声能量等先验知识的条件下重构效果不理想的问题,本文对StOMP算法主要进行两个方面的改进:(1)将环境噪声包络服从瑞利分布的特性与StOMP算法的迭代残差相结合,使得原子选择判决门限自适应化,无需依靠经验提前设定判决阈值;(2)利用残差比阈值对StOMP算法的迭代终止条件进行修正,实现重构算法的盲停止。
2 基于CS理论的宽带频谱感知模型
压缩感知理论应用的前提是信号具有稀疏特性或近似稀疏特性,设认知用户的检测带宽为B,将它均匀划分为N个子频带,这N个频带互不重叠。主用户可以随意占用这些子频带,对于未被占用的子频带 ,它们的功率谱密度(Power Spectrum Density,PSD)接近于零,因此PSD在频域上表现有一定的稀疏特性[10]。
设待检测的宽带信号为x(t),它可以表示为:
(1)
式中αi表示第i个子频带的幅值,fi表示第i个子频带的中心频率,n(t)表示信号所处环境的噪声和,在一定信噪比条件下,可以近似为零。由于本文主要研究的是频域稀疏信号,因此将信号x(t)表示到频域得
s=F·x
x=Finvs
(2)
F为离散傅里叶变换基矩阵,Finv为离散逆傅里叶变换基矩阵,向量s为x的频谱,s中只有K个系数不为零(K y=ΦFinvs=As (3) y为M×1维观测向量(M≪N),Φ为一个与稀疏变换基不相关的M×N维测量矩阵,A为M×N维传感矩阵,需要满足约束等距特性(Restricted Isolated Property,RIP)和非相关性等条件才能实现信号的重构。 对于式(3)的求解,可以通过求解基于l0范数最小化的问题完成对信号的恢复。 s.t.y=As (4) 此方法求得的解是最优解,但由于M 通过以上对宽带频谱的压缩采样与恢复,本文构建宽带压缩频谱感知模型,如图1所示。 图1 宽带压缩频谱感知模型Fig.1 Broadband compressed spectrum sensing model StOMP算法是对OMP算法的一种改进策略,针对OMP算法每次迭代时只选择一个原子而使循环次数过大的问题,StOMP算法的改进思路是设定一个门限,每次迭代更新子坐标集时选择幅值大于该门限所对应原子的坐标,简化了OMP算法的循环迭代次数,提高了运行速度,适合解决大规模数据重构问题。 StOMP算法的流程如下: 输入:观测矩阵Φ,测量值y,最大迭代次数T,阈值τ。 (1)初始化。残差向量r0=y,索引集Λ=∅,子坐标集J=∅,迭代计数t=1。 (3)更新支撑集ΦΛ,其中,Λ=Λ∪J。 从上述算法流程可以看出,StOMP算法主要存在以下两方面的不足: 1)在选择原子时,原子选择判决门限中的阈值参数τ往往依靠经验来决定,一旦设定便无法调整,这存在一定的局限性,并且阈值τ设置的合理与否将会对算法最终的重构性能产生很大的影响。另外,判决门限中的‖r‖2中有一部分能量属于噪声能量,在较低信噪比环境下噪声能量将占据残差能量的绝大部分,因此判决门限值的大小往往具有不确定性,判决门限过高,迭代难以停止,判决门限过低,则可能大量选入无用原子,严重影响重构质量。 2)在迭代终止条件方面,StOMP算法依据是否达到最大迭代次数T或者残差能量是否小于阈值ε来判定。然而,最大迭代次数的依据是信号的稀疏度,而能量阈值往往依据的是信噪比,无论稀疏度还是信噪比,这类先验知识在实际环境中很难直接获得,因此,StOMP算法的迭代终止条件存在一定局限。 针对上述的不足,本文提出了ATO-IStOMP算法。 目前国内外研究学者在改进贪婪类算法上所做的主要工作有两大类:一类是针对重构算法在低信噪比环境下重构效果不佳的问题而对重构算法进行去噪或抗噪的改进,例如文献[12]针对噪声折叠现象对重构算法的影响,提出了一种基于选择性测量的去噪重构算法(denoising OMP),明显改善了重构算法在低信噪比下的重构性能,然而该算法没有实现在未知稀疏度条件下的盲重构,因此使用范围受限;另一类是针对重构算法在未知稀疏度或信噪比等先验知识情况下重构性能不佳的问题而对重构算法进行的“盲改进”,稀疏度自适应匹配追踪(Sparsity Adaptive Matching Pursuit, SAMP)算法[13]的提出代表重构算法能够在盲稀疏度条件下实现信号重构,但是其迭代终止条件中阈值的设置需要信噪比作为先验知识,而实际环境中信噪比往往未知,因此应用范围受限;针对这一问题,文献[14]通过引入残差比阈值修正了SAMP算法的迭代终止条件,实现了信噪比较低且未知环境下的精确重构,但是在步长的选取对最终重构精度的影响方面分析不足;文献[15]提出了一种近似梯度下降算法,该算法通过逐步迭代逼近的方式以求得方程的最优解,进而恢复原始信号,但是该算法没有对信号的稀疏度进行估计,而是借用Beck等人提出的快速收缩阈值算法来确定稀疏度与信号误差之间的权值,对于重构过程中适应性问题的研究有待进一步加强。针对上述问题,本文从判决门限和迭代停止条件两个方面对StOMP算法进行改进,提出了一种ATO-IStOMP算法。 目前传输系统通常是在较低信噪比的环境下进行频谱感知和数据传输的,且感知环境的噪声通常为高斯加性白噪声,噪声包络服从瑞利分布,其概率密度函数为 (5) 由 (6) 得ρ的概率分布函数 (7) 式中ρ表示噪声包络,σn表示噪声标准差。文献[16]证明了如果变量z服从瑞利分布,则其中值Z满足 (8) 则 (9) 所以 (10) 式中|ni|表示噪声序列n第i个元素的包络,median(x)是对数列x求中值运算。文献[17]首次提出通过设置适当的门限来实现去噪过程。文献[18]将这一思想应用到了压缩感知信道估计的恢复算法中,给出了门限设定准则 (11) 式中α为可调参数,R为信道的抽头时延个数。 由于压缩感知贪婪类算法每次迭代的残差能量一部分来自于噪声,特别是当信噪比较低时残差的大部分能量来自于噪声,由此认为迭代残差的幅值近似服从噪声分布特性,可将噪声分布特性与迭代残差相结合,对StOMP算法的原子选择判决门限进行修正。式(11)、(12)可以表示为 (12) (13) 式中|ri|为残差向量第i个分量的幅值,N为待恢复信号的长度,α为可调参数,取值范围为[0.5,2],与信噪比等先验知识无关。修正后的判决门限优点有:(1)无需根据经验提前设定阈值;(2)修正后的判决门限根据感知环境中的噪声能量进行自适应调整,能够起到较好的抗噪效果,增强算法本身的鲁棒性。 根据上一节StOMP算法的流程可以看出,最大迭代次数T的设定需要预知信号的稀疏度,迭代终止阈值ε的确定依据的是噪声能量,不足之处在于: (1)当信号稀疏度和信噪比未知时,T和ε很难准确设定,而这两个参数的设定准确与否将直接影响算法的重构精度。 (2)在低信噪比环境下,‖r‖2的能量基本逼近噪声能量,不会随迭代次数的增加而明显降低,即迭代到一定次数以后,‖rt-1‖2与‖rt‖2基本不变,如果阈值ε设定的不准确,可能会造成StOMP算法难以终止,严重影响重构精度。 文献[19]针对传统迭代终止条件的不足,即迭代残差能量小于某个固定阈值。利用残差比阈值对SAMP算法的迭代终止条件进行修正。使得改进后算法的重构性能提高。 首先,在低信噪比条件下的测量值y可以分解为 (14) (15) (16) (17) 由于宽带频谱感知往往是在低信噪比环境下进行的,并且在实际的工程应用中,感知环境的噪声能量特性无法提前获得。由此可以得出残差比阈值迭代终止条件适合于本文所研究的频谱感知场景,因此将其引入到StOMP算法的迭代终止条件中。 4.1和4.2小节分别对StOMP算法的原子选择判决门限和迭代终止条件进行了改进,现将ATO-IStOMP算法的流程介绍如下。 输入:观测矩阵Φ,测量值y。 (1) 初始化。残差向量r0=y,索引集Λ=∅,子坐标集J=∅,迭代计数t=1。 (3) 更新支撑集ΦΛ,其中,Λ=Λ∪J。 由以上流程可以看出,ATO-IStOMP算法不需要信号稀疏度和信噪比等先验知识,而是根据每次迭代残差向量的分布情况进行原子自适应选择,并且通过残差比阈值迭代终止条件实现了该算法的盲停止,在低信噪比环境下有良好的重构性能。 仿真技术平台为Pentium(R) Dual-Core (3.06 GHz) CPU、2G内存的PC机,所有实验均在Matlab 2014a环境下进行,下面分别从预设参数α对重构算法的影响、宽带频谱的重构效果、重构概率和重构精度四个方面对ATO-IStOMP算法进行分析。 首先分析在无噪条件下参数α对算法重构概率的影响。选取α的变化范围为0.3~0.7,间隔为0.1,待测信号长度N为256,测量维度M=128,观测矩阵为M×N维高斯随机观测矩阵,稀疏度变化范围为5~70,间隔为2,针对每个稀疏度进行蒙特卡洛仿真1000次,取均值,仿真结果如图2所示。 图2 无噪条件下不同参数对重构算法的影响Fig.2 Comparison of reconstruction probability of algorithm under different parameters under no-noise condition 图2所表示的是ATO-IStOMP算法在不同参数α下重构概率随稀疏度变化而变化的对比示意图,由图可知,α在0.3~0.7范围内变化时对ATO-IStOMP算法的重构性能影响不大,当信号稀疏度在5~35范围内时,ATO-IStOMP算法在各个参数值α下均能以100%的概率重构原始信号,当信号稀疏度大于35时,ATO-IStOMP算法的重构概率在各个参数下均有不同程度下降,其中ATO-IStOMP算法的参数为0.3或0.7时,其重构性能略微低于算法在参数0.4~0.6范围变化时的重构性能,原因在于如果参数α过低或过高,将导致原子选择判决门限过低或过高,从而影响候选集原子质量,进而影响到最终的重构性能。 当环境中存在噪声时,由于在有噪条件下迭代残差的能量较无噪时大,所以每次迭代时残差与观测矩阵各列的相关系数也会随之受到影响,这时需要调整ATO-IStOMP算法中的预设参数α的变化范围为1.7~2.1,稀疏度取15,信噪比变化范围为-3~20 dB,针对每个信噪比进行蒙特卡洛仿真1000次,取均值,其余条件不变。仿真结果如图3所示。 图3 有噪条件下不同参数对重构算法的影响Fig.3 Influence of different parameters on reconstruction algorithm under noisy conditions 图3表示的是有噪条件下当参数α在1.7~2.1范围内变化时对重构算法性能的影响。由图可知,α在1.7~2.1的范围内变化对ATO-IStOMP算法的重构性能影响较弱,当信噪比为-3~0 dB时,ATO-IStOMP算法在参数值α为1.7或2.1条件下的重构性能略微低于在参数值1.8~2.0范围内的重构性能,原因在于ATO-IStOMP算法在参数值α为1.7或2.1条件下会导致原子判决门限稍微偏低或偏高,信噪比较低时,环境噪声能量较高,这样可能会误将能量较高的噪声当作有用原子选入候选集,进而影响重构性能;当信噪比大于1 dB时,参数α在1.7~2.1范围内变化对ATO-IStOMP算法的重构性能基本没有影响。 总之,ATO-IStOMP算法的优势在于不需要知道信号的稀疏度以及环境噪声能量等先验信息,而判决门限参数α是一个相对确定的预设参数,当重构环境无噪声时,α只需在0.5左右的范围内取值即可,当重构环境有噪声时,α只需在1.9左右的范围内取值即可,与信号和环境具体的先验知识无关。 本次实验待检测信号长度N为256,稀疏度为25,测量维度M=128,观测矩阵为M×N维高斯随机观测矩阵,参数α取0.5,阈值θ取0.25。仿真结果如图4所示。 图4 ATO-IStOMP算法恢复结果Fig.4 ATO-IStOMP algorithm recovery result 由图4可以看出,ATO-IStOMP算法在未知信号稀疏度条件下无论是在频点方面还是在信号幅值方面都能够实现信号的精确重构,一定程度上说明了本文提出ATO-IStOMP算法的可行性。 为了分析比较ATO-IStOMP算法的重构概率性能,选取OMP、StOMP、GOMP[20]算法与其进行比较。首先比较各个算法在无噪条件下的重构概率,稀疏度变化范围为5~70,间隔为2,针对每个稀疏度进行蒙特卡洛仿真1000次,取均值,其余仿真条件不变,仿真结果如图5所示。 图5 无噪条件下各算法重构概率对比Fig.5 Comparison of reconstruction probability of each algorithm under no-noise conditions 图5给出了各算法在无噪条件下重构信号的仿真结果,由图可知,各个算法的重构概率随着稀疏度的增大而降低,这是由于稀疏度越大,信号内包含的信息量越大,重构信号时需要观测矩阵的原子个数越多,然而观测矩阵中的原子是固定的,因此当稀疏度较大时有限的原子组合种类能够表示信号的可能性就较小。当稀疏度在20以下时,各算法均能以100%的概率精准恢复信号;稀疏度在25~43时,OMP和StOMP算法的重构性能开始缓慢下降,当稀疏度为43时,OMP算法的重构概率为34.9%,StOMP算法的重构概率为70.2%,两者都无法满足重构需求,信号基本失真; GOMP是对OMP算法的一种改进算法,在每次迭代过程中选择多个原子,使得迭代效率提高,因此在无噪条件下的重构性能优于OMP算法,然而随着信号稀疏度的增加,GOMP算法难免由于选入过多原子从而造成原子候选集冗余,影响重构性能,因此ATO-IStOMP算法的重构概率曲线优于GOMP算法。 在实际的工程应用中信号往往伴随着噪声,下面对各算法在有噪条件下的重构概率进行仿真实验,信噪比变化范围为-3~20 dB, 针对每个信噪比蒙特卡洛仿真1000次,取均值,信号稀疏度设为15,原子判决门限参数α为1.9,其余条件不变,实验结果如图6、图7所示。 图6 信噪比为2 dB时各算法重构概率对比Fig.6 Comparison of the reconstruction probability of each algorithm when the SNR is 2dB 图6给出了不同算法在信噪比为2 dB环境下重构概率随稀疏度的变化而变化的规律,由图5和图6可知,不同算法的重构性能在低信噪比环境下均受到噪声的影响,这是由于重构算法对噪声比较敏感,在恢复信号的过程中会将某些噪声能量较高的频点当作信号来恢复,导致恢复的信号存在一定误差。同时可以看出,在较低信噪比环境下ATO-IStOMP算法的重构概率曲线优于其他算法的曲线,原因是当信噪比较低时,通过增大参数α可以提高ATO-IStOMP算法自适应门限的鲁棒特性,能够更好地利用残差向量幅值类似于噪声分布的特性进行原子的自适应选择,起到了良好的去噪效果,同时ATO-IStOMP算法的残差比阈值迭代终止条件也具有良好的抗噪声性能。 图7 各算法在不同信噪比下的重构概率对比Fig.7 Comparison of the reconstruction probabilities of different algorithms at different SNR 由图7可知,不同算法的重构概率随信噪比的增大而提高,原因是信噪比越高,信号中各噪声频点能量越小,重构算法受噪声影响越小,重构性能越好。ATO-IStOMP算法的重构概率曲线优于其他算法,当信噪比为3 dB时,OMP、StOMP、GOMP算法的重构概率均低于90%,信号恢复效果不理想,ATO-IStOMP算法的重构概率接近95%,信号恢复效果较好。 为了分析ATO-IStOMP算法在较低信噪比环境下的重构精度,选取均方误差(Mean Square Error,MSE)作为分析指标: (18) 待检测信号稀疏度为15,信噪比变化范围为-3~12 dB, 其余仿真条件与5.3节有噪情况下的一致,仿真结果如图8所示。 图8给出了不同算法在低信噪比环境下重构信号的均方误差对比情况,从图中可以看出,各算法的重构误差随着信噪比的增加而降低。其中ATO-IStOMP算法的重构均方误差低于StOMP算法,这是由于前者从原子选择判决门限和迭代终止条件两个方面对后者进行了去噪改进,增强了后者的抗噪声性能,因此前者在低信噪比下的重构精度高于后者。StOMP算法是对OMP算法的一种改进,每次迭代选择多个原子而不是选择一个原子,简化了OMP算法的迭代过程,但这种改进策略是以降低恢复精度为代价的。经计算,在重构均方误差为10-3时,ATO-IStOMP算法相比于OMP算法信噪比改善约0.6 dB, OMP算法相比于StOMP算法信噪比改善约1 dB。 图8 不同算法在低信噪比环境下的重构精度对比Fig.8 Comparison of reconstruction accuracy of different algorithms in low SNR environment 通过理论研究和仿真实验表明,本文利用残差比阈值迭代终止条件使ATO-IStOMP算法能够在盲稀疏度条件下较为精准地恢复信号频谱,而自适应判决门限使得ATO-IStOMP算法在低信噪比条件下的重构性能相比于其他算法有较为显著的提升,通过以上两个方面的改进,ATO-IStOMP算法适用于低信噪比、盲稀疏度条件下的频谱重构。
3 StOMP算法分析

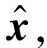
4 ATO-IStOMP算法
4.1 原子选择判决门限改进思想
4.2 迭代终止条件的修正
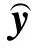


4.3 ATO-IStOMP算法介绍

5 仿真分析
5.1 预设参数α对算法重构性能影响分析


5.2 重构效果分析

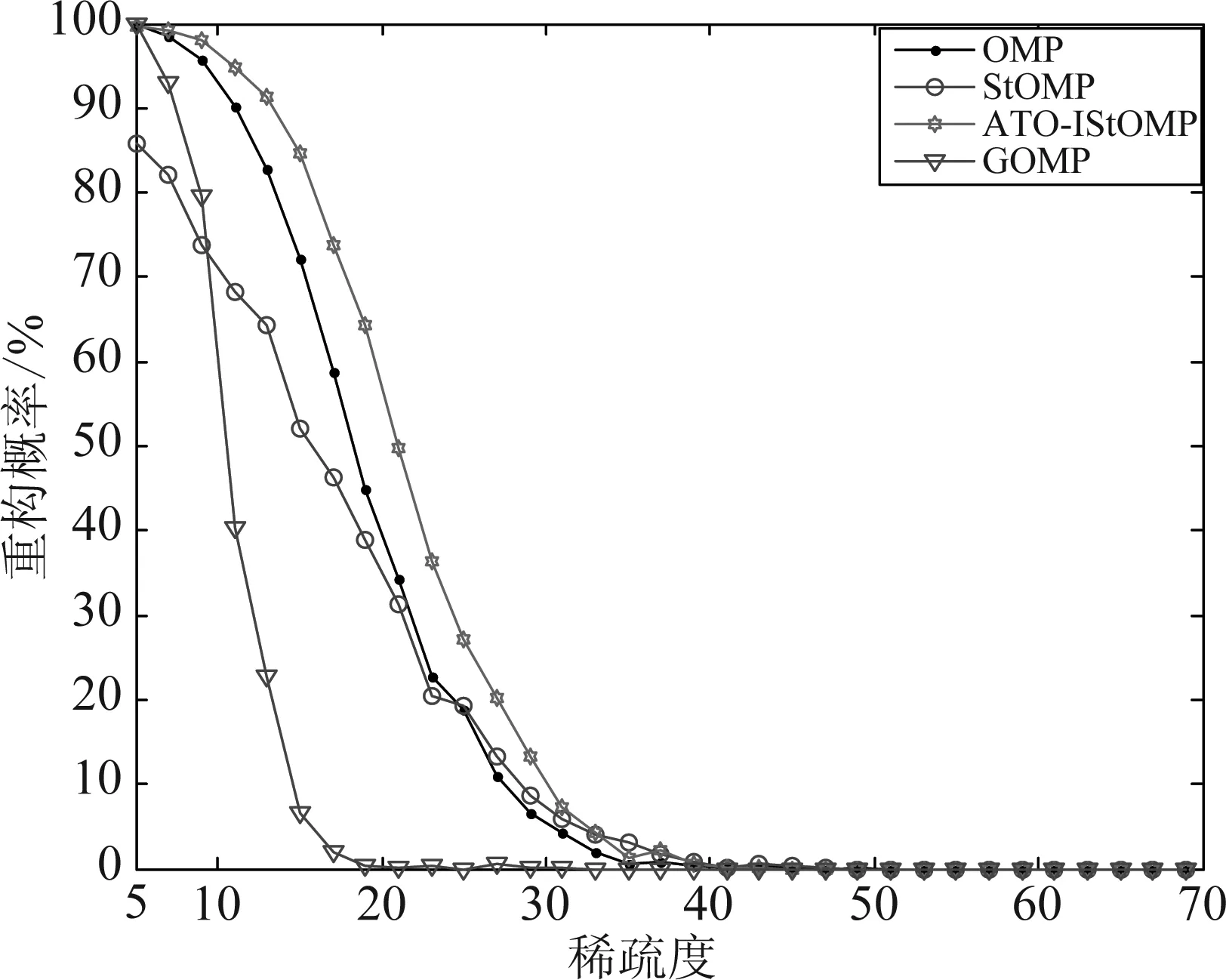
5.3 重构概率分析


5.4 重构精度分析

6 结论

