地下水DNAPLs污染多相流的随机模拟及其不确定性分析

王 涵,卢文喜*,李久辉,常振波,侯泽宇 (1.吉林大学环境与资源学院,吉林 长春 130000；2.吉林大学地下水与资源环境教育部重点实验室,吉林 长春 130000)

石油类有机污染物难溶于水,泄漏进入地下环境后对地下水造成污染,且难以去除,严重威胁人类健康[1].这类有机物进入地下环境后通常以非水相流体(Non-aqueous phase liquids,NAPLs)的形式存在[2].非水相流体根据密度的不同可分为两类[3-4],密度小于水的称为轻非水相流体(Non-aqueous phase liquids,简称 LNAPLs);密度大于水的称为重非水相流体(Dense non-aqueous phase liquids,简称 DNAPLs).

DNAPLs具有高密度,低水溶性和高界面张力的特性[5],比LNAPLs更难修复.为了合理高效地防治地下水DNAPLs污染,常常需要开展地下水DNAPLs污染风险评价工作.地下水DNAPLs污染风险评价的研究通常以多相流数值模拟为基础.然而,多相流数值模拟模型中水文地质参数存在很大的不确定性[6].水文地质参数的不确定性会导致多相流数值模型输出结果的不确定性.因此,地下水污染风险评价也具有不确定性[7].对多相流数值模拟模型中水文地质参数的不确定性进行定量分析,可以使地下水DNAPLs污染风险评价结果更加科学、全面.

近年来,不确定性分析在地下水溶质运移方面发展迅速.Goodrich等[8]应用蒙特卡洛方法进行不确定性分析,借助复杂数值模拟模型来模拟从假想污染场地到地下排水渠的溶质运移过程; Hassan[9]应用MCMC方法(Monte Carlo Markov Chain)方法评价了Amchitka Island (Alaska) Milrow试验场地下水模型参数的不确定性;陈彦等[10]研究了含水层渗透系数空间变异性对地下水溶质运移数值模拟结果造成的影响;吴吉春等[11]提出了将地下水数值模拟不确定性分析结果与风险评估相结合,在此基础上,常振波等[12],李久辉等[13]分析了参数不确定性对地下水溶质运移数值模型输出结果的影响,并从风险评估的角度对不确定性分析结果进行阐释.然而,这些研究均是针对简单的二维单相流算例,目前尚未见有关于多相流随机模拟及不确定性分析的报道.本文将不确定性分析与地下水DNAPLs污染多相流的随机模拟相结合,运用灵敏度分析法筛选对模型输出结果影响较大的参数,作为模型中的随机变量;为减少反复调用多相流模拟模型产生的计算负荷,运用克里格方法建立多相流模拟模型的替代模型,并利用替代模型完成蒙特卡洛随机模拟.最后,对多相流模拟模型输出结果进行统计分析并完成了地下水污染风险评价.根据污染物浓度分布函数估算单井遭受污染的风险.绘制地下水污染风险分区图,从而对全区地下水遭受不同程度污染的风险大小进行分区,为地下水污染防治提供合理依据.

1 研究方法

1.1 蒙特卡洛法

蒙特卡洛法是一种以概率和统计理论为基础的具有广泛实际应用价值的数学方法.它的基本思想是针对待求问题,根据物理现象本身的统计规律,或人为构造一合适的依赖随机变量的概率模型,使某些随机变量的统计值为该待求问题的解.通过进行大量统计实验,得到该问题的解.

蒙特卡洛法是分析复杂数值模型不确定性最有效的方法之一[14].它假设随机变量概率分布函数和协方差函数已知,人工产生多组输入变量,然后对每组输入变量运行数值模型,获得多组模型计算结果[15].本文运用蒙特卡洛方法进行地下水DNAPLs污染多相流的随机模拟.

近年来,蒙特卡罗方法越来越多地应用于地下水数值模拟不确定性分析方面.束龙仓等[16]利用蒙特卡罗方法,以济宁市地下水潜水含水层为例,分析了给水度空间分布的随机性对地下水库库容计算结果的影响.温忠辉等[17]运用蒙特卡罗方法,在开采量不确定的条件下,对数值模拟结果进行可靠性分析,并对比计算了在不同的给定允许降深条件下,模拟结果的可靠性.束龙仓等[18]应用蒙特卡罗法,研究水文地质参数的不确定性对地下水补给量计算结果以及地表水与地下水交换量的影响.陆乐等[19]利用蒙特卡罗方法对多尺度非均质含水层中的溶质运移进行了模拟.综上,蒙特卡罗方法在国内地下水模拟不确定性分析方面得到了广泛应用.

1.2 灵敏度分析法

灵敏度可度量一种因子变化对另一因子的影响程度.灵敏度分析的方法主要有全局灵敏度分析法和局部灵敏度分析法[20].本文利用局部灵敏度分析的方法,评价单一参数变化对模型输出结果造成的影响.计算时通过对参数求偏导数反映参数变化对模型输出结果的影响程度,公式如下:

Xk表示当参数αk变化时对输出结果y的影响程度,即灵敏度系数.

某一参数k的灵敏度系数值,可通过保证其他所有参数不变,使该参数k的值由αk变为αk+Δαk,相应的因变量值由 yi(αk)变化为 yi(αk+Δαk),用下列计算获得其计算值,即:

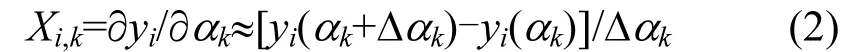
由于不同参数的单位不同,导致灵敏度系数就无可比性,因此本文采用下列标准化无量纲形式计算灵敏度系数[21],即:

1.3 替代模型

地下水DNAPLs污染多相流的随机模拟需要反复多次调用多相流模拟模型.为减少上述计算负荷,应用克里格方法,建立地下水DNAPLs污染多相流模拟模型的替代模型.在蒙特卡洛模拟过程中可以直接调用模拟模型的替代模型.

克里格方法是常用的地质学统计方法之一[22],它从变量的相关性和变异性出发[23],在有限的研究区域内,对区域中变量取值进行误差最小的优化估计.克里格方法利用协方差的变化来表达空间的变化,现被延伸为一种建立替代模型的方法,是一种黑箱模型[24].建立替代模型要完成以下几个步骤:

式中: R ( xi,xj)(i = 1,2， … m; j = 1,2， … m )代表采样点xi和点 xj的关联函数.关联函数模型包括很多种,本文采用应用最为广泛的高斯模型,模型形式如下:

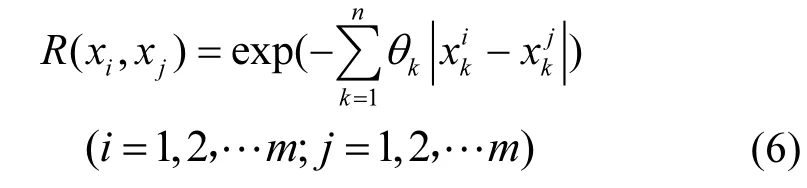
式中:θk为待定系数,xki是第i个样本的k维坐标.

根据克里格模型,在预测点 x点处的响应值 y(x)的预测估计值为

式中:f为基函数,为方便起见,本文选择常数型, f为一常数列向量;r( x)为点x与n个训练样本采样点(x1,x2,… xn)之间的相关向量;y为与n个采样点对应的响应值,为n×1的向量;β为线性回归部分的待定参数,可以通过最优线性无偏估计求得:

R为n个采样点的相关矩阵:

方差σ2的估计值为:

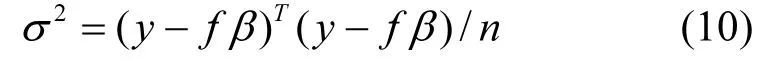
替代模型的建立可以通过求解上面的非线性无约束优化问题来实现.待定参数θk可以通过一个无约束优化问题求得:

2 应用研究

2.1 模型建立

本文针对假想算例展开研究.模拟研究场地为140m×60m×20m的三维区域,计算目的层为松散岩类孔隙潜水含水层.含水层介质为均质各向同性介质.地下水流方向由左向右.左右边界为定压边界(左边界压力为 102.972kPa,右边界压力为 101.325kPa),其余边界为隔水边界.在研究区内,有一个硝基苯泄漏点,泄漏量为 8m3/d,泄漏时间为 10d.硝基苯浓度为70%(体积分数).模拟时间持续 300d,模型中各参数取值见表 1.潜水含水层污染物初始浓度为 0.研究区内污染源与观测井的平面位置见图1.

在研究区水文地质概念模型的基础上建立地下水DANPLs污染多相流数值模拟模型.多相流数值模拟模型由偏微分方程和定解条件两部分组成.偏微分方程以质量守恒定律为理论基础[25],公式如下:

图1 研究区污染源与观测井位置示意Fig.1 Location of the pollution source and observation wells in study area

表1 模型参数取值情况Table 1 Values of model parameters

式中:k代表不同组分的标号,k值取1,2时分别代表水,油;l代表不同相标号,l取1,2时分别代表水相、油相.φ代表孔隙度;Ck代表k组分的总浓度(体积分数);Ckl代表 k组分在 l相中的浓度(体积分数);ρk代表 k组分的密度(量纲为 ML-3);Sl代表相 l的饱和度;代表 k组分在 l相的弥散系数张量(量纲为 L2/T);Rk代表 k组分总的源汇项;→代表 l相的渗透流速(量纲为 L/T);krl代表相 l的相对渗透率;代表固有渗透率(量纲为 L2);ρl代表相 l的密度(量纲为 ML-3);g代表重力加速度(量纲为LT-2);z代表垂向距离(量纲为 L);Pl代表相 l的压力[量纲为 M/(L⋅T2)].

定解条件包括初始条件和边界条件两部分.初始条件如下式所示:

式中:Ckl0(x, y, z)代表k组分在l相中的初始浓度(体积分数); Sl0(x, y, z)代表 l相的初始饱和度;Pl0(x, y, z)代表l相的初始压力分布(量纲为ML-1T-2).边界条件如下式所示:

图2 研究区剖分示意Fig.2 Subdivision schematic diagram of study area

2.2 灵敏度分析法筛选随机参数

灵敏度分析可以定量评价参数不确定性对模拟模型输出结果造成的影响.利用灵敏度分析方法筛选对模拟模型输出结果影响较大的参数,作为模型中的随机变量,既减少计算负荷,又提高研究精度.

表2 各井各参数灵敏度计算结果Table 2 Sensitivity results of each parameter of each well

进行灵敏度分析时,将模型中各参数取波动范围内均值,见表3,输出一组污染物浓度值.再分别将模型中各参数加减 20%,10%,同时保证其他参数不变,分别输出污染物浓度值.利用公式(3)计算各井各参数灵敏度系数值,见表 2,并筛选出两个灵敏度较大的参数作为模型中的随机变量.

图3 1号井参数灵敏度分析Fig.3 Sensitivity analysis of No.1 well

图4 2号井参数灵敏度分析Fig.4 Sensitivity analysis of No.2 well

由图3,图4,图5可知,对于1、2、3号井,灵敏度较大的两个参数均为孔隙度和渗透率.将孔隙度和渗透率作为随机模拟过程中的随机变量,将其他参数作为常数.

图5 3号井参数灵敏度分析Fig.5 Sensitivity analysis of No.3 well

2.3 拉丁超立方抽样

本文替代模型的输入变量为随机模拟过程中的随机变量,即孔隙度和渗透率,输出变量为污染物浓度.建立模拟模型的替代模型需要一定数量的训练样本和检验样本,为使样本具有代表性,应用拉丁超立方抽样方法在孔隙度、渗透率的合理变化范围内进行抽样.

拉丁超立方抽样是一种基于分层采样的抽样方法,具有较高的采样效率,能覆盖到所有采样区间.它对变量按照假定的概率密度等概率划分,在每个区间内抽取等数量的参数组成参数样本.根据前人经验可知,孔隙度服从正态分布,渗透率服从对数正态分布[26].

运用 MATLAB软件编写拉丁超立方抽样程序,通过两次抽样分别获得40组训练样本,和10组检验样本.

表3 参数概率分布及取值情况Table 3 Values and probability distribution of model parameters

2.4 替代模型的建立及基于替代模型的随机模拟

将50组样本输入地下水DNAPLs污染多相流模拟模型中,利用UTCHEM软件进行求解,获得50组输入-输出样本数据集.利用训练样本建立替代模型,并利用检验样本检验替代模型对模拟模型的逼近精度.

由图6可知,替代模型与模拟模型输出结果的相对误差均小于0.80%,误差较小,故认为替代模型精度较高,可以用来代替模拟模型.

运用蒙特卡洛法进行地下水DNAPLs污染的随机模拟.首先,将孔隙度和渗透率作为随机变量,利用拉丁超立方抽样获得1000组参数组合;然后,将1000组参数组合输入替代模型,输出1、2、3号井1000组污染物浓度数据;最后,对1、2、3号井污染物浓度数据进行统计分析.

图7 各井污染物浓度累计频次Fig.7 Pollutant concentration histogram of each observation well

3 结果与讨论

3.1 地下水污染情况分析

3.1.1 单井污染物浓度统计分析 对3口观测井各1000组污染物浓度数据的各项统计指标进行分析,绘制3口观测井污染物浓度累计频次直方图(图7).1号井污染物浓度在 20～40mg/L范围内的概率高达83.5%,可以预测 300d后 1号井污染物浓度在20～40mg/L范围内的可能性最高.同理可以预测,300d后 2、3号井污染物浓度 50～90mg/L和 10～30mg/L范围内的可能性最高.由表4可以看出,2号井污染物浓度数据的变异系数较小,分布较集中.3号井污染物浓度数据的变异系数较大,分布较分散.这说明,在同一时间条件下,污染物浓度的不确定性大小主要取决于观测井和污染源的距离.距离污染源越近,污染质运移的距离越短,受含水层各参数的影响越小,所以,污染物浓度的不确定性就越小.

在同一空间位置的条件下,以3号井为例,经计算,第 100,200,300d污染物浓度数据的变异系数分别为0.12,0.25,0.31.这说明在相同位置处,污染物浓度不确定性的变化速率不与时间成正比,增速逐渐降低.其他位置同理.

表4 各观测井污染物浓度输出值统计指标Table 4 Statistical indexes of pollutant concentration of observation well

图8 研究区地下水污染程度分区Fig.8 Contour map of contaminant concentration in study area

3.1.2 全区地下水污染情况分析 为划分全区地下水遭受不同程度污染的区域,以第 10层为例,计算每个剖分网格各 1000组污染物浓度的均值,绘制等值线图(图8).假设污染物浓度超过20mg/L为轻度污染区域,超过40mg/L为中度污染区域,超过60mg/L为重度污染区域.由图8可知,300d后研究区轻度污染区域面积约为2715m2,占全区总面积的32.3%.严重污染区域面积约为825m2,占全区总面积的18.5%.

图9 各井污染物浓度分布函数曲线Fig.9 Pollutant concentration distribution function of each observation well

3.2 地下水污染风险评价

3.2.1 单井污染风险评价 利用 MATLAB软件将各井污染物浓度数据作为随机变量,绘制污染物浓度分布函数曲线(图9).假设污染物浓度超过20mg/L为轻度污染,超过40mg/L为中度污染,超过60mg/L为重度污染.由图9可知1,2,3号井为轻度污染的风险分别

为 92%,100%,40%,为中度污染的风险分别为20%,99%,0%;为重度污染的风险分别为 0%,51%,0%.由风险评价结果可知,3号井水质较好,该井附近适宜人类居住.

3.2.2 全区地下水污染风险评价 为了对全区地下水 遭受不同程度污染的风险大小进行分区,以第 10层为例,计算1000个剖分网格处地下水轻度污染、中度污染以及重度污染的风险,绘制地下水遭受不同程度污染的风险分区图.由图 10可知,在地下水遭受轻度污染的条件下,当污染风险依次为30%,60%,90%时,风险分区的面积呈现逐渐减小的趋势.由图11、12可知,中度污染和重度污染的结论同上.比较图10、11、12可知,在污染风险一定(30%,60%或90%)的条件下,当地下水分别遭受轻度、中度、重度污染时,风险分区的面积逐渐减小.

综上,在污染程度相同的条件下,污染风险越大,风险分区的面积越小;在污染风险相同的条件下,污染程度越重,风险分区的面积越小.地下水污染风险分区图可以帮助决策者分析出地下水污染的高风险区,估计高风险区的位置和面积,合理开展地下水污染风险评价工作,为地下水污染防治提供更加科学可靠的依据.相关人员也可以根据地下水污染风险分区图,选择人类宜居地点.

图10 地下水轻度污染风险分区Fig.10 Contour map of groundwater mild pollution risk

图11 地下水中度污染风险分区Fig.11 Contour map of groundwater moderate pollution risk

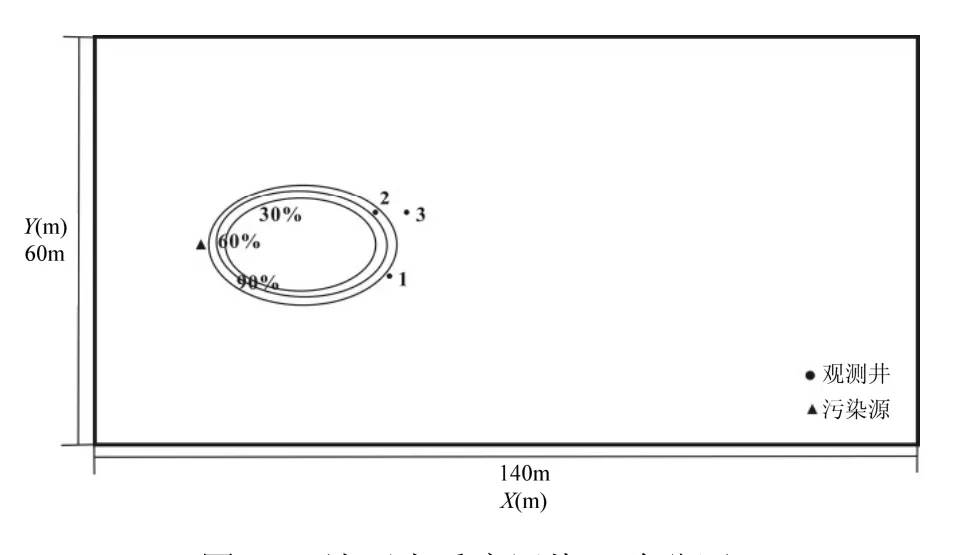
图12 地下水重度污染风险分区Fig.12 Contour map of groundwater serious pollution risk

4 结论

4.1 灵敏度分析结果显示:地下水DNAPLs污染多相流模拟模型中孔隙度和渗透率的灵敏度较大.利用灵敏度分析法可以筛选对模型输出结果影响较大的参数,减小不确定性分析的工作负荷.

4.2 本文运用克里格方法建立了地下水 DNAPLs污染多相流模拟模型的替代模型.既能大幅度减少不确定性分析过程中的计算负荷,还可以保持较高的精度.

4.3 本文分析了水文地质参数不确定性对多相流数值模拟模型输出结果的影响.利用蒙特卡洛方法进行地下水DNAPLs污染多相流的随机模拟,并对随机模拟结果进行统计分析.利用污染物浓度分布函数估算单井遭受污染的风险;利用地下水污染风险分区图分析地下水污染的高风险区,为地下水污染的防治提供合理依据.