不确定理论下带惩罚机制的城市污水处理期望收益模型
张 林,李存林,2*,李 丹 (.北方民族大学数学与信息科学学院,宁夏 银川 75002;2.北方民族大学管理学院,宁夏 银川 75002)
随着我国城市化率和生活水平的提高,城市产生的污水越来越多.此前,我国主要靠政府建设污水处理厂处理污水.现在,政府对污水处理都进行了市场化管理,外包(BOT)给专业企业[1].这使得政府和污水处理企业形成了委托代理关系,随之也带来了“道德风险”问题:政府无法准确评估企业实际的污水处理量,造成双方信息不对称.这种不对称可能引发企业的投机行为,即:为了追求利润最大化,企业不顾污水处理过程中,不确定性因素对实际污水处理量的影响,恶意提高签约量,使签约量大于实际处理量,来获取更多利润.这可能造成大量污水得不到及时处理,甚至导致城市环境污染或城市环境公共危机事件.由此造成环境和社会利益负的外部性,政府还可能为此埋单.为了降低委托代理关系中的道德风险,维护政府和社会公共利益,预防污水处理企业恶意提高签约量的投机行为,政府必须在与企业签订外包合同时[2-3],引入惩罚机制降低道德风险.引入惩罚机制,致使企业充分、合理地评估生产中可能存在的不确定因素,客观、科学地确定签约量.
国内外学者对城市污水处理的研究主要分为两类.一类研究污水处理的生物化学方法及工艺流程.如:污泥对水中硫化物的吸附特性[4]、冬季硝化强化与微生物种群分析[5]、污水地下渗滤系统强化脱氮试验的研究、化学强化、污染物分析、城市废水指标[6-8]等方面;另一类研究污水处理过程的优化与管理.如排污权价格对污水处理投资决策的影响[9]、污水处理系统最优控制[10]、企业运营成本的污水处理费制度[11]、城镇污水处理设施空间优化配置[12-13]等.第二类研究在涉及污水处理量时,都将其刻画为一个确定的数值.事实上,污水处理实践中常常遇到一些复杂的、主观的和不确定的因素[14],如管理不善、工人操作失误、设备故障、天气情况等,影响企业实际完成的污水处理量.因此,许多学者将企业实际污水处理量刻画为随机变量[15-19].众所周知,随机变量依赖于事件的可重复性.现实中,很多企业无法收集到足以估计其处理量的历史数据,也无法找到其统计规律.企业只能让同行专家利用经验判断或不完全的数据做出粗略估计[20].从另外角度看,之前专家对污水处理问题的研究,都聚焦在企业内部处理方式的优化或处理技术的更新.没有学者从政府与企业关系角度研究污水处理问题.
针对以上不足,本文从以下两个方面进行改进:一是引入公理化的不确定决策空间,将企业污水处理量刻画为不确定空间中的不确定变量.这种不确定变量,不依赖于历史统计数据,只依赖于专家对污水处理企业的经验评估.这种经验评估是建立在公理化不确定系统上,使得这种处理方式更科学,更合理;二是从政府和企业的关系角度,在污水处理的模型中引入惩罚机制,抑制企业决策中的“道德风险”.
1 研究方法
现实中,企业处理污水量受众多因素的影响,每次影响正常生产的原因也不尽相同.这些影响生产的不确定因素,通常也是无规律可寻.一方面,如果污水处理企业有很多条生产线,企业可以在不同的生产线同时收集数据,很容易收集到估计产量分布规律的统计数据.而实践中,污水处理企业只有一两条相同的生产线,不具备同时收集污水处理量统计数据的条件,统计数据的收集只能一年一年积累,要收集到足以估计其产量概率分布的大样本,需要几年的时间,这对实际生产几乎没有指导意义.另一方面,随着居民生活水平的变化,污水成分也发生变化,处理技术也在更新,整个企业生产条件发生变化,造成之前收集的数据和现在的数据不具备同分布的性质.这种背景下,用概率变量估计污水处理量显然是不科学的,也不可行.当然,也有学者利用专家经验进行估计,用主观概率刻画污水处理企业的实际处理量,然后用概率理论进行处理.这些学者忽略了专家的经验估计相对于统计数据是较为粗略的.主观概率又是建立在概率理论可加测度上的理论,将这种粗略的经验估计变量用在具有可加性的概率测度上,意味着人为将专家粗略估计的变量假定为一个相对精确的统计变量.这使得专家的经验估计在运算中具有了可加性.而理论上没有人证明主观经验具有可加性,实践中也不可能有人相信一个主观的经验判断还具有可加性.这种用概率理论或主观概率理论处理专家主观经验数据,必然造成企业对自己实际污水处理量估计的过度自信,导致企业签约量大于实际处理量.在具有惩罚机制的条件下,企业触发惩罚条款的可能性大增,收益也会受损.若由于乐观估计造成的过多签约污水,得不到及时处理,还可能导致环境危机事件.
本文引入 Liu[20-21]提出的公理化不确定理论.这种理论中的不确定变量,不依赖于事件的可重复性,只依赖于行业专家对实际状况的经验评估,这种经验评估不但是建立在非可加测度基础上的,而且是建立在公理化系统上的.这有效的避免了主观概率系统中,主观经验估计具有可加性的弱点.
定义1[20]设Γ是一个非空集,l是Γ上的一个σ−代数,l上的元素Λ称为事件,M{Λ}是事件Λ发生的信度. Λc是Λ在l上的补集.若以下三个公理
公理1. (规范性公理) 对于全集Γ,有M{Λ}=1.
公理 2. (对偶性公理) 对于任意事件Λ,有M{Λ}+M{Λc}=1.
公理3. (次可加性公理)对于事件Λ1, Λ2,⋅⋅,Λn,⋅⋅⋅,有则称M为一个不确定测度,称三元集(Γ,l,M)为一个不确定空间.
定义 2[20]设ξ是一个不确定变量,则Φ(x) = M { ξ ≤x}是ξ的分布函数,其中x∈ℜ.
定理 1[20]设ξ是一个具有不确定分布Φ的不确定变量,若它的期望值存在,则期望值为

定义3 一个不确定变量ξ满足

则称ξ是线性的,且服从线性不确定分布,记为ξ ~ L[a,b].
定理 2[22]设ξ是一个具有不确定分布Φ的不确定变量,若 f(x)是一个严格单调(单增或单减)函数,则存在期望值
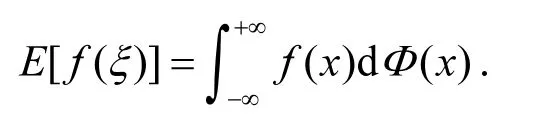
2 模型的建立与求解
如引言所述,政府在与污水处理企业签订委托代理合同时,应增加惩罚条款,以遏制企业“道德风险”.模型中政府对污水处理企业的惩罚机制设计为:对未完成的污水量,按照合约价乘以一定的惩罚率实施惩罚.
2.1 模型假设
(1)假定企业实际污水处理量为不确定空间的不确定变量.
(2)假设政府能提供给企业足够的污水量,若污水供给量不足,政府应按签约量支付费用;
(3)对企业的惩罚只针对签约量中未完成部分,对完成部分按照合同计价;
(4)一切不可抗力因素导致的不良后果,由政府和企业双方共同承担,不影响签约效果.
现在给出模型中使用的符号说明
x企业与政府签约的污水量(万t), Qx≤≤0,Q表示政府提供给企业的污水量,假设 Q足够大;ξ企业实际能够处理的污水量(万t),是不确定变量,0≥ξ;p污水处理费用单价(元/t),0≥p;c处理污水的总成本费用单价(元/t),0>>cp;v政府对企业违约部分的惩罚率,0>v;)(xµ污水处理企业收益(万元).
2.2 模型构建
设企业实际能够处理的污水量ξ是一个不确定变量,具有不确定分布Φ.如果企业污水签约量是 x,则收益不确定函数μ(x)为

注:企业污水处理量ξ在年初签订合约时是一个不确定的量,但到了年终, ξ是具体的确定值.因此,算子min{x,ξ}虽然是不确定变量与确定变量的取小运算,实践中仍然是有意义的.根据目标函数(1),考虑带惩罚机制的污水处理问题,可建立如下期望收益模型.
定义 4 设污水处理企业的收益小于μ*的最大不确定指数要小于等于β,则基于不确定理论的污水处理期望收益模型为
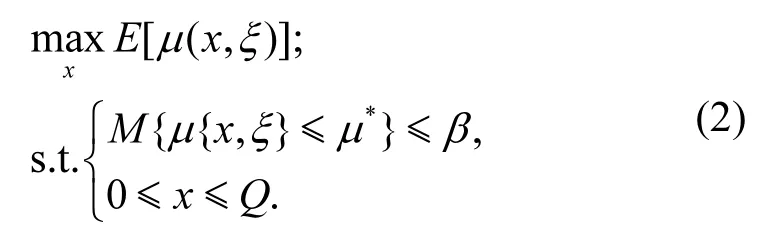
式中:β为企业所能承受的最大不确定指数(0≤β≤1),μ*是污水处理企业的保守收益.
2.3 模型转化与求解
模型(2)是不确定规划,要用去不确定性的方法,将其转化为等价的经典数学规划求解.
定理 3 设政府对未完成污水量的总价值(x−ξ)p以惩罚率v进行惩罚,若ξ~L[a,b],则带惩罚机制的污水处理期望收益为

证明 因ξ服从线性不确定分布 L [ a,b],分布函数为 Φ (t ) ,(t∈ℜ+).μ( x,ξ)是关于ξ的单调递增函数,将(1)式代入E[μ( x,ξ)],根据定理2及线性不确定分布 L [ a ,b]的性质[20-21]可得

积分可得

证毕.
对于约束条件
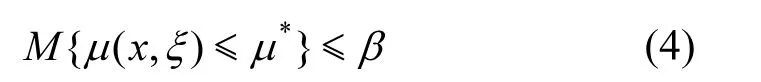
又ξ是一个不确定变量,根据文献[20]可知μ( x, ξ)是 不 确 定 变 量 的 函 数,连 续 且 单 调,用D ( v ,β,μ*)表示可行解的集合,可得如下定理
定理4 模型(2)可行解集合具有下列性质:
(1)若 D ( v ,β,μ*)是空集,则污水处理企业就会放弃和政府进行签约;
(2)若 D ( v ,β,μ*)非空,则

证明 将(1)式代入约束条件(4)式,可得

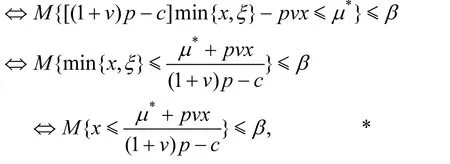
或

(1)由*式,有

此时企业不会选择和政府签约,即可行集D ( v ,β,μ*)是空集.
(2) 若 D ( v ,β,μ*)非空,对*式,可行解 x应满足同理,对**式,有

综上所述,若 D ( v ,β,μ*)非空,则满足

证毕.
因此,模型(2)可转化为下列等价模型(6).
定义 5 不确定理论下带惩罚机制的污水处理期望收益模型为

其中,E[μ(x,ξ)]满足(3)式,x∈ D (v,β,μ*)满足(5)式.
3 数值算例
政府以每吨 p = 3元将本城市部分污水委托给某企业处理,企业处理污水的成本为每吨 1=c 元,政府对未处理完污水量惩罚率为 1.0=v ,企业实际污水处理量]200,150[~Lξ, 即150=a万t,200=b万t.则基于不确定理论,带惩罚机制的污水处理企业期望收益(3)式为

设企业保守收益为300万元,则可行集(5)式为
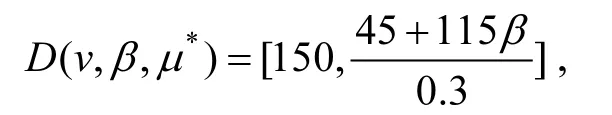
若,05.0=β则模型(6)为

用Matlab软件算出最优解 17.169=x 万t,最大期望收益89.329=µ万元.如图1

图1 期望收益和签约量关系Fig.1 Expected return and contract volume
图1中第1、2、4条竖线分别代表两个区间:外围区间 [1 50,200]为目标函数的分段区间,前面第1、2条竖线表示约束集 [1 50,507.5/3],第 3条竖线代表期望收益函数的全局最优解xq.分析图1可知,当企业承受的不确定指数为 0.05时,企业受到可行集的约束.当x取最大约束值 xj=507 . 5/3(≈169.17)时,得到最大收益值为 329.89万元.当 xj大于全局最优解xq= 1 93. 4 8时,函数图中有极大值点(193.48, 343.48),此刻企业获得稳定的最大收益值343.48万元.
4 结果与分析
下面利用Matlab软件的粒子群算法分别对模型中的参数:不确定指数β、惩罚率v、不确定度区间[a , b]取不同的值,求得相应的污水签约量x和期望收益E[µ],然后再分别讨论各个参数值的变化对结果的影响,及实际意义.
4.1 对不确定指数β的讨论
结合上面算例,取

则计算如表1

表1 期望收益、签约量和不确定指数的关系Table 1 Expected return, contract volume and uncertain index
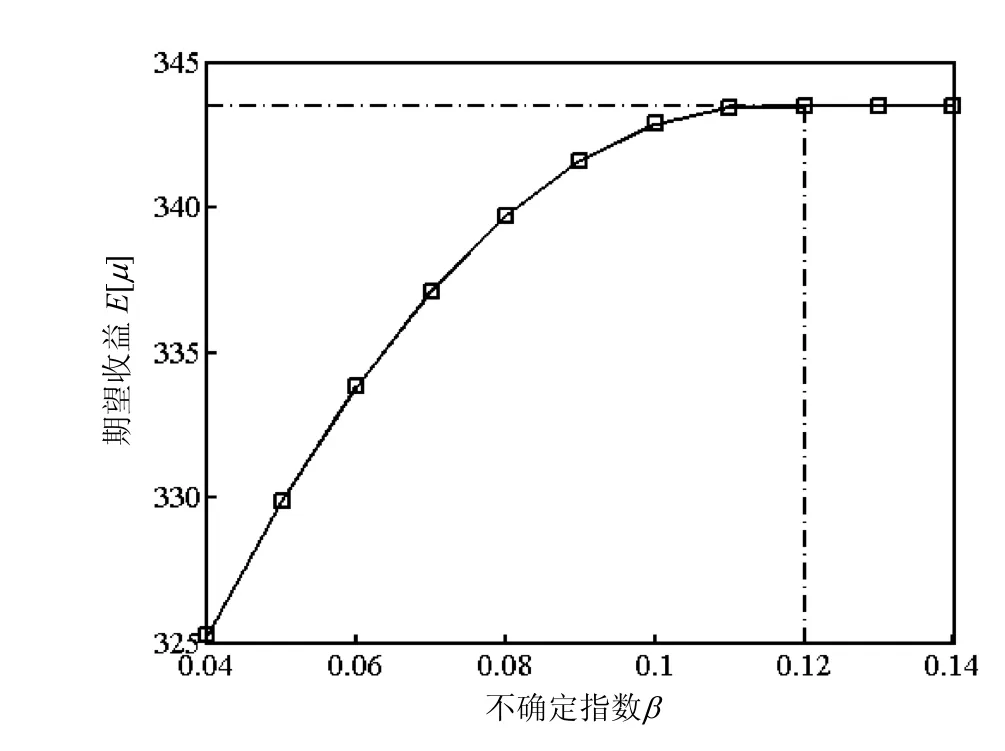
图2 期望收益和不确定指数的关系Fig.2 Expected return and uncertain index
从图2、图3和表1可知,(1)惩罚率不变的条件下,随着企业所能承受的不确定指数β的逐渐增加,签约量逐渐增大,期望收益也快速增加.当β增加到 0.12时,][µE和x均达到最大值.(2)当β大于0.12以后,其对期望收益和签约量将不在有影响.因为随着β增大,可行集范围渐渐扩大.可行集的右端点值已经超过了期望收益函数的全局最优解 48.193=q x ,之后全局最优解xq保持不变,且在企业污水处理能力范围 ]200,150[之间,固然最大收益值不变(如图1).

图3 签约量和不确定指数的关系Fig.3 Contract volume and uncertain index
4.2 对惩罚率v的讨论
同样地,结合上述算例取 p = 3,c = 1, µ*=300,β =0.05,[ a , b]=[150,200],可得


表2 期望收益、签约量和惩罚率的关系Table 2 Expected return, contract volume and penalty rate

图4 期望收益和惩罚率的关系Fig.4 Expected return and penalty rate
从图4、图5和表2可知,(1)给定不确定指数,随着惩罚率的增大,签约量逐渐减小,期望收益也减小.(2)当惩罚率达到0.7时,签约量达到最大值154.88万t,收益达到最大值308.79万元.若惩罚率继续增大,签约量减小较为缓慢,惩罚率对签约量的影响减小.此时,企业签约量已接近无风险生产量a,企业违约的不确定指数比较低,惩罚对企业的影响较小;(3)当v较小时,x和E[µ]减小非常快,说明惩罚因子具有明显遏制企业签约量的作用.换句话说,惩罚因子较小时,企业签约量较大,违约风险也较大,此时增加惩罚率,对企业道德风险具有明显抑制作用.(4)若没有惩罚因子,企业最大签约量就会选择为最大设计产能 200,此时企业违约风险很高.

图5 签约量和惩罚率的关系Fig.5 Contract volume and penalty rate
4.3 对无风险处理量a的讨论
类似上面取p=3,c=1, µ*=300, v = 0.1,β=0.05,可得模型为


表3 期望收益、签约量和a值的关系Table 3 Expected return, contract volume and a value
当企业签约量为a时,企业违约的不确定指数为0,a称为无风险处理量.a与企业管理能力有关,如果管理水平高,影响正常生产的不确定因素就减少,企业无风险处理量就提高,收益也就增加.利用Matlab软件计算如表3.
结合表3、图6和图7分析可知,在一定的不确定指数β和惩罚率v下,随着无风险处理量a的取值逐渐增大,签约量x逐渐增大,期望收益E[μ]也在逐渐增大.(1)从图6中观察到E[μ]一开始的增大趋势相比x较大,这是因为在企业刚开始提高管理水平,降低不确定因素时,降低了企业的违约指数,也就大大的降低了企业违约的惩罚成本,此时,管理能力提高对企业的效益提高具有明显的贡献.(2)当a的值大于 110时,从图6和图7发现,x和E[μ]增加较为缓慢,这是因为随着企业的无风险处理量a逐渐增加,企业的管理经营水平逐渐提升,经营管理水平提高对企业效益的显著影响逐渐降低,也就是x和E[μ]的增加速度降低,这正好符合经济学中的边际效益递减规律,因此出现了图6和图7的现象.综上分析,建议企业应该加强内部控制与管理,降低影响污水处理的不确定因素,提高无风险处理量a,可有效的增加期望收益.

图6 期望收益和a的关系Fig.6 Expected return and a

图7 签约量和a的关系Fig.7 Contract volume and a
5 结论
5.1 企业签约量越大,收益越高,所承受的风险也越大.这符合企业生产与风险的经济学现象.
5.2 惩罚率越高,企业签约量越小,收益也随之减少.说明惩罚因子起到了重要的作用:有效地降低了企业的投机行为和道德风险.
5.3 企业的无风险处理量越高,企业的签约量越大,收益也越大.说明企业运行中要加强内部管理运营,努力提高无风险处理量.

