装配线平衡与物流配送路径协同优化*

吴永明，罗利飞，戴隆州，徐艳霞，张 晗

(贵州大学 a.现代制造技术教育部重点实验室；b.贵州省公共大数据重点实验室；c.机械工程学院，贵阳 550025)

0 引言

装配线平衡问题(Assembly line balancing problem,简称ALBP)是制造领域一种较重要的NP问题，装配线平衡与否之间影响企业的生产效率、市场竞争力以及生产的成本，随着客户的需求更加苛刻，使得交货周期更短，企业必须通过以较低的成本快速对客户所需产品进行应对。

彭慧等[1]对混流装配线第二类平衡的问题进行了研究，采用遗传算法对建立的加权生产节拍和平均负荷模型进行了求解，但加权是单独考虑各影响因素，没有把各因素之间的影响进行直观反映；刘炜琪等[2]建立了最小化超载时间、产品变化率及总切换时间多目标优化模型，并提出一种改进的多目标粒子群算法进行求解。李明等[3]采用提出一种变异粒子群算法对ALBP问题进行求解，在标准的粒子群算法基础上，对设定步长内位置没有更新的个体采用多点变异，并采用纵向进化与横向搜索机制，提升综合搜索能力，但只是对装配线进行了求解。杨家平等[4]针对物料配送路径优化问题，提出一种新型的单亲遗传算法对车间物料运送通道的节点数学模型进行了优化，但物流配送模型过于简单化。高贵兵等[5]建立了车辆行驶距离最短、车辆利用率最大和配送次数最少为优化目标的多目标模型，并用双层递进进化算法对模型进行了求解，但仅限于物流配送。

目前，国内外研究大多数采用装配线平衡和物料配送分开研究，与实际的企业生产有一定的出入，物料配送低效制约装配线高效生产，增加产品生产制造周期，本文通过对装配线平衡模型与物料配送模型分别进行分析，建立装配线平衡与物料配送协同优化模型，运用改进的多目标算法进行求解，实现与生产的更紧密配合。

1 装配线模型构建

问题描述：在装配线的新建或者改建当中，都要重新对装配线进行平衡求解，在满足装配作业之间先后关系约束和生产节拍条件下，把装配工序在每一个工作站进行合理分配(最少工作站)的同时考虑工作站的均衡系数，以及在平衡中配送物料的物料小车行驶总路径是否最短，在装配线平衡的同时确定配送路线。

假设：①装配线上工人的技术水平不存在差异，可以完成任一项作业；

②一个作业元素的作业时间不依赖于位置和工位；

③装配线的节拍大于作业元素时间中的最大者；

④作业元素可以分配到任何工作站，即作业元素没有位置约束；

⑤一个工序只能分配给一个工作站；

⑥物料在储存区直接配送。

模型的建立：

F=min(N,SI,D)

(1)

(1)在给定节拍的条件下求出最小工作站：

(2)

s.t .Si∩Sj=⊄，i≠j,i,j=1,2,...,N;

(3)

t(Sn)≤CT,n=1,2,...,N

(4)

∀i∈Sx,j∈Sy,若pij=1，则x≤y

(5)

其中，Sn表示分配到工作站n的作业元素集合，t(Sn)表示第n个工作站的总作业时间，式(2)为一个作业元素只能分配到一个工作站内，即每个作业元素不能重复分配到多个工作站，式(4)为每个工作站的总作业时间必须小于等于节拍CT。

(2)装配线均衡系数：

(7)

其中ti表示第i个作业元素的作业时间，N表示工作站数目，M表示总作业元素数目。

(3)物流方面在一定装载的运输车辆最少和运输的路径和最短：

(7)

(8)

(9)

(10)

(11)

N表示工作站数，K表示配送物料的车辆数，li为配送中心到第i个工作的距离，xij为决策变量，第j辆车配送第i个工作站的物料，若是，xij=1，否则，xij=0，式(7)表示车辆运输的最短路径，式(8)表示每个物料点都能得到配送且只能由一辆车完成，式(9)为每辆车配送路线上物料和不超载，式(10)表示每辆车都从配送中心出发，式(11)表示每辆车配送完后返回配送中心。

2 改进的 NSGA-II算法设计

2.1 基本算法

NSGA-II[6]是目前优化效果不错的一种元启发式多目标[7]智能算法，通过快速非支配排序，使算法复杂度降低，加快算法的运行，同时精英策略在进化过程中，父代的优秀个体可以保留到子代中，不但能提升种群的多样性，而且优秀个体的遗传使得算法结果的精确性得到优化，但是NSGA-II侧重于全局的广域搜索，局域搜索深度较差，因此，在保留原算法优点情况下，对拥挤度比较算子、对变异做出了改进，同时根据实际模型对编码及解码作出了改进。

2.2 编码设计

染色体的编码由(0～1)的随机数组成，编码及解码过程[8]：

某装配线作业任务顺序如图2所示，对应的染色体编码及解码见表1。

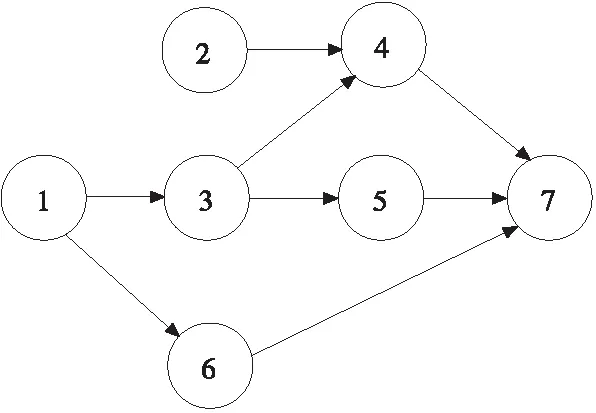
图2 某装配线作业任务顺序图

表1 编码解码操作

2.3 拥挤度计算以及改进

拥挤度是指在群体中的给定个体的周围个体的密度[9]。结合装配线模型，以及NSGA-II计算拥挤度的缺点，拥挤距离采用空间上的欧几距离，即：

(12)

式中，f1,f2,f3分别为两个子目标函数。

拥挤度改进后计算流程如图3所示。

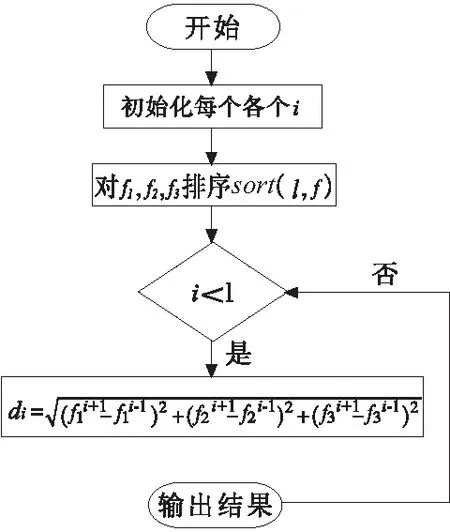
图3 拥挤度流程图

2.4 高斯变异和混沌扰动变异算子

本文通过根据NSGA-II算法容易陷入局部最优问题，将高斯变异和基于Tent映射的混沌优化嵌入改进拥挤度的NSGA-II算法中，通过改变算法的初始和精英保留过程，不但可以加快算法收敛速度，提升算法初始优化速率，而且在算法后期削弱精英策略及时跳出局部最优，提高算法鲁棒性，使算法更适用于所建立的模型。

(1)高斯变异

高斯变异[10]是指在进行变异操作时，将变异随机参数，用服从均值为μ，方差为σ2的正态分布随机数来替代，表达式为：

(13)

由正态分布图的特征可以看出，高斯变异侧重搜索原个体附近的某个局部区域，有较好的局部搜索能力，能算法搜索全局极小点更加高效，更加精确。

(2)混沌搜索

混沌搜索是指搜索为非线性搜索，但是却有一定的规律性、遍历性、随机性，规律性是指由确定的方程式导出变量，遍历即不会重复遍历空间的所有状态，使得算法容易跳出局部极值。

产生混沌序列的方法很多，根据Tent映射[11]值分布比较均匀且平坦，选用此映射产生混沌序列，公式如下:

(14)

其中，Xd为混沌序列X的第d维变量，xd为服从高斯分布(正态分布)的随机数。

高斯变异和混沌扰动的变异步骤为：

①首先用Tent映射产生一个混沌变量；

②将混沌变量映射回目标解空间：

(15)

式中，maxx和minx表示染色体的最大最小值。

③进行混沌扰动：

(16)

3 实例分析

为了验证NSGA-II对模型求解的有效性和可行性，通过MATLAB对Buxey问题进行仿真和分析，该问题包含29个作业任务，给定其工作节拍CT=41，作业顺序如图4所示，车辆最大的装载容量maxweight=10。工作站到配送中心的距离及工作站间的距离如表2所示，作业任务加工时间和物料需求在表3给出。

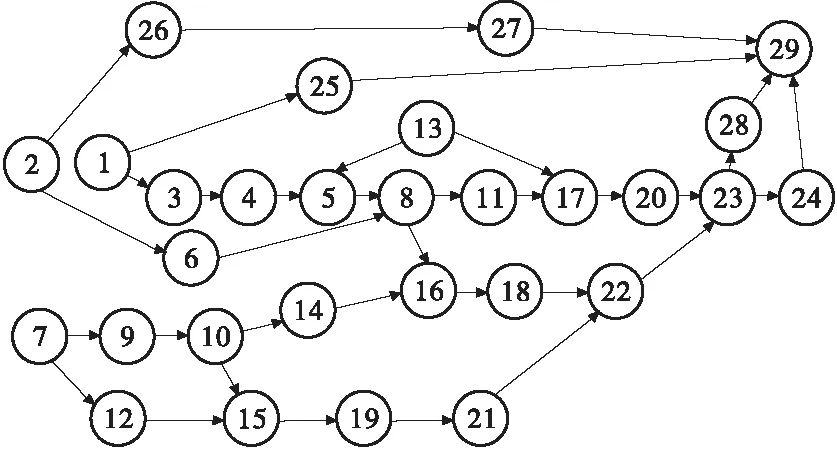
图4 装配线作业任务顺序图

表2 工作站间距离(m)

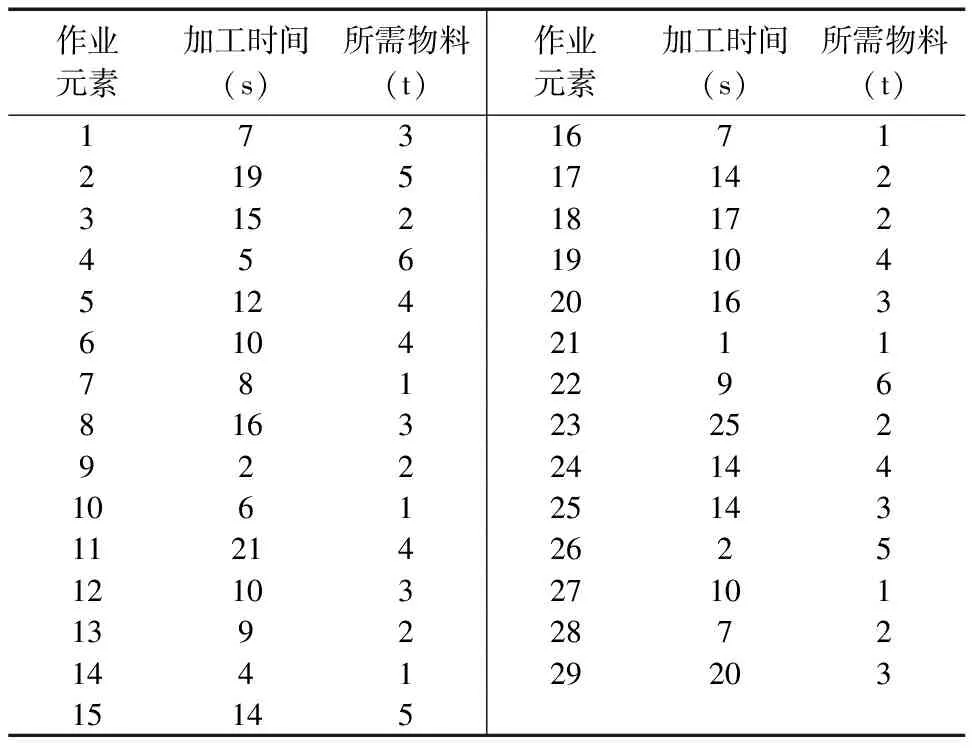
表3 工序加工时间和物料需求

算法参数如下：种群规模pop=100交叉概率Pc=0.9变异概率Pm=0.1，进化50代最后得到若干非劣解，选取求解结果如图5所示。

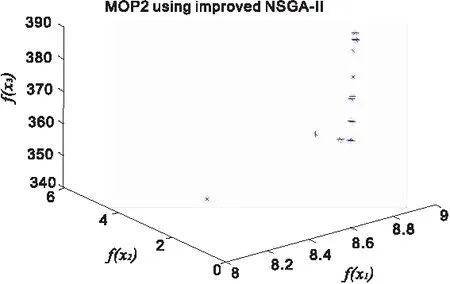
图5 Pareto解

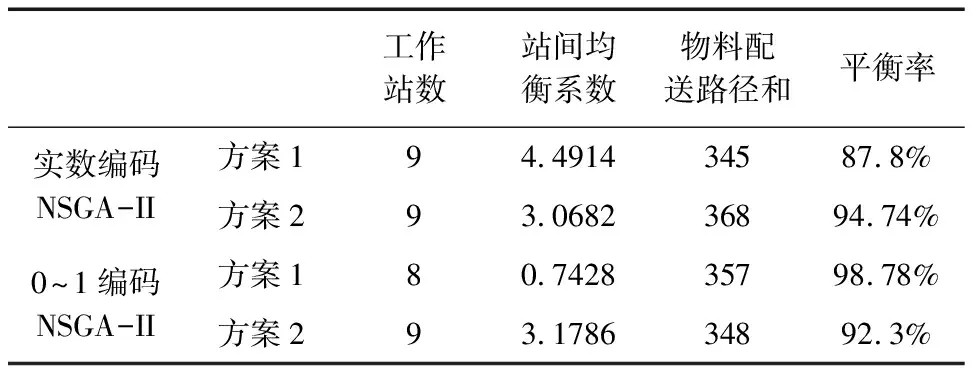
表4 最优解

图6 方案1

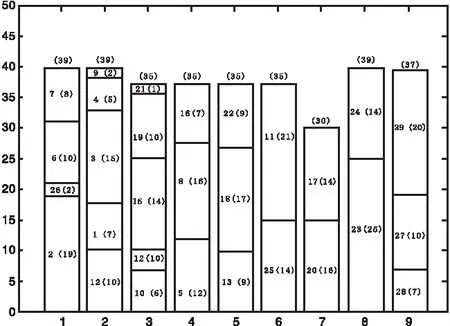
图7 方案2

从图5看出有最优Pareto解，和选取两个Pareto解如图6和图7所示，目标值在表4给出，装配线各项指标值均较优，算法的寻优能力较强，同时说明提出的多目标模型具有一定的有效性，该模型可供生产决策者在实际生产需求中根据实际情况选择合适方案。

4 结束语

本文针对现有装配线模型和物料配送模型进行分析，建立装配线平衡和物料配送路径协同模型，在保证装配线平衡的同时，保证了物料的配套性和协调性，从装配线工作站、装配线负荷均衡化、物料配送路径三个方面构建了符合实际情况的多目标模型。通过改进的NSGA-II算法对多目标模型求解，对实例结果的分析表明，0～1编码保证了初始种群的随机性，改进的拥挤度和拥挤距离能扩大算法初始搜索种群，基于Tent映射的混沌优化嵌入NSGA-II算法中，能有效跳出局部优化，提高装配线利用率，在生产抉择中提供更确切的帮助。