带有初速度的S形路径轨迹规划方法*

史伟民，沈 波，杨亮亮

(浙江理工大学 机械与自动控制学院 ，杭州 310018)

0 引言

在数控机床、机械臂等工业领域中，运动轨迹的控制方法常常采用S形加减速控制[1-3]。与指数型加减速和直线型加减速等控制方法相比，S形加减速控制具有运动过程平稳、较小冲击和振荡、速度曲线光滑等优势[4-6]。S形加减速控制其生成位移轨迹为加速度连续变化的位移曲线，其曲线光滑，能有效的减少冲击，实现平滑启停，减少残余振动和冲击，非常适用于高速高精运动控制[7]。

一般的S形加减速控制方法为三阶位移点到点运动控制方法。陆莲仕等[8]提出了一种具有恒定速度段的点到点运动轨迹规划方法，能使加速度曲线的拐点平滑过渡，且计算简单，但该规划方法使运动时间变长，降低了效率。穆海华等[9]研究了一种三阶点到点运动的轨迹规划方法，考虑了轨迹可能存在的情形并给出对应的规划方法，具有一定的普遍性。但该方法分类复杂，计算繁琐，不具有较强的实践性。以上方法只针对始末速度都为零的情况下所进行的规划，而实际应用中，有可能会出现需要在运动过程中改变速度的情况。例如在工业滴料过程中，滴料对象不均匀时，依靠改变滴料喷压不够灵活，容易造成滴料溢出，而采用滴料喷头实时变速的方法可以避免这种情况。

杨亮亮等[10]提出了一种基于牛顿迭代法的S形加减速时间算法，解决了在带有初速度的情况下，对运动进行重新规划，其中应用了牛顿迭代法来解得一种五元非线性方程组的近似解并完成轨迹规划。但牛顿迭代法求解的迭代次数不可控，使得该方法难以进行实时规划。

为此，本文提出了一种带有初速度的S形路径规划方法，考虑了在匀速运动过程中，具有目标位移的情况下，对运动进行重新规划，并具有极高的实时性。

1 带有初速度的轨迹规划条件分析

1.1 轨迹规划问题描述

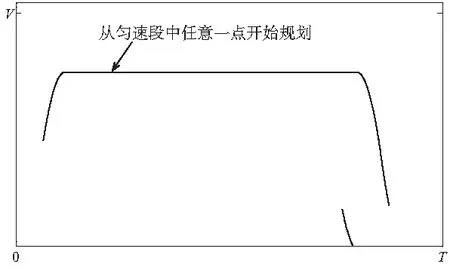
图1 原始运动速度轨迹

在匀速运动过程中对运动重新进行轨迹规划，可以转化为带有初始速度vs的情况下进行轨迹规划的问题。如图1所示，以匀速运动过程中任意一点为起点，读取剩余目标位移s和初速度vs，设置中间速度vm。其中，若vm大于vs，则进行先加速到vm，再减速到0的规划；若vm小于vs，则进行先减速到vm，再减速到0的规划。运动轨迹为三阶轨迹，如图2所示为先加速再减速的运动规划，为方便理解运动过程，将整体运动过程划分为从vs运动到vm过程的第一运动阶段，匀速运动过程的第二运动阶段，从vm减速到0过程的第三运动阶段。

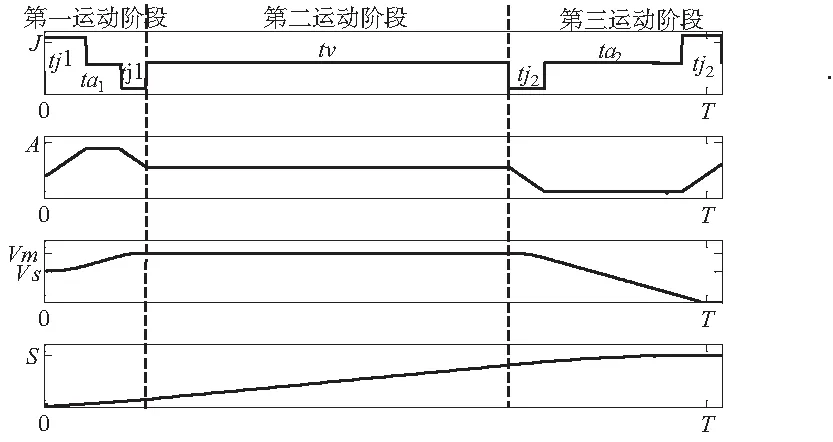
图2 带有初速度的运动各状态轨迹

1.2 动力学约束条件

在系统运动过程中，必须根据运动系统动力学、加工工艺和加工精度等要求对运动速度、加速度、以及加加速度进行实时控制，保证在整个运动过程中上述指标不超过设定的要求，以减少冲击与残余振动，实现平滑启停。针对带有初速度的轨迹规划，如图2所示，应该满足以下约束要求。

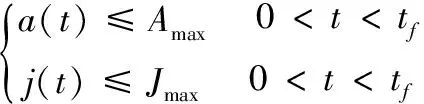
a(t)——轨迹加速度曲线；

j(t)——轨迹加加速度曲线；

Amax——允许的最大加速度；

Jmax——允许的最大加加速度。

其中，第一运动阶段中加加速度段的时间量为tj1，匀加速度段的时间量为ta1，第三运动阶段中加加速度段的时间量为tj2，匀加速度段的时间量为ta2，第二运动阶段时间量为tv，则tf=2tj1+2tj2+ta1+ta2+tv。

1.3 已知条件

轨迹曲线运动始末状态为已知条件，如式(2)所示，且运动的剩余目标位移s，动力学约束Jmax，Amax， 中间速度vm已知。

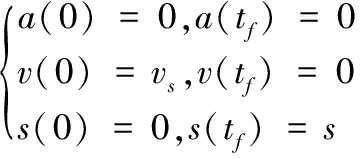
(1)

1.4 积分条件

插补过程中，其位移s、速度v、加速度a、加加速度j应满足下式所描述的积分与微分关系：

(2)

2 轨迹规划算法分析

根据vm设置的不同，轨迹规划分为先加速再减速规划和先减速再减速规划两种。由图2可知，将运动过程分为三个运动阶段，共最多7个时间段组成，因此只需求出每个时间段的时间量，即可得到运动轨迹。其中，先加速再减速规划中，第一运动阶段为加速阶段，第二运动阶段为匀速阶段，第三运动阶段为减速阶段；先减速再减速规划中，第一运动阶段与第三运动阶段都为减速阶段，第二运动阶段为匀速阶段。

2.1 先加速再减速规划

2.1.1 第一运动阶段规划

第一运动阶段最多可由三个时间段组成，运动过程的约束条件为：

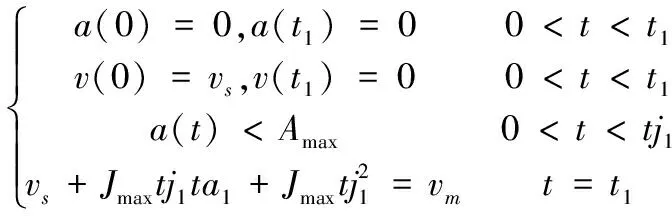
(3)

其中，t1=2tj1+ta1

先考虑效率最优时，ta1=0，则速度约束方程简化为：

(4)

则，计算得到：

(5)

然而，此tj1可能不满足加速度约束，由积分条件可得第一运动阶段的最大加速度为：

A1=Jmaxtj1

(6)

若A1Amax，则令A1=Amax，重新计算tj1：

(7)

至此，tj1已最终确定，将tj1带入速度约束方程中计算得到：

(8)

tj1和ta1均已知，根据积分条件可以计算出第一运动阶段的位移s1：

(9)

2.1.2 第三运动阶段规划

第三运动阶段与第一运动阶段相似，最多由三个时间段组成，运动过程的约束条件为：

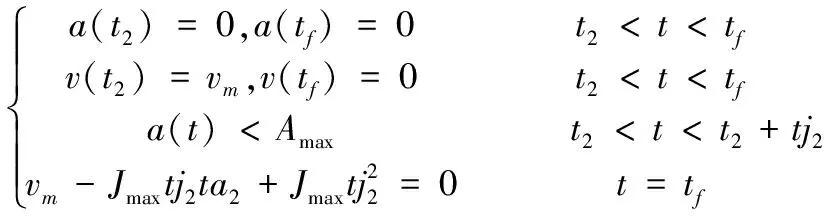
(10)

其中，t2=2tj1+ta1+tv。

先考虑效率最优时，ta2=0，则速度约束方程简化为：

(11)

则，计算得到：

(12)

然而，此tj1可能不满足加速度约束，由积分条件可得第三运动阶段的最大加速度为：

A2=Jmaxtj2

(13)

若A2Amax，则令A2=Amax，重新计算tj2：

(14)

至此，tj2已最终确定，将tj2带入速度约束方程中计算得到：

(15)

tj2和ta2均已知，根据积分条件可以计算出第一运动阶段的位移s3：

(16)

`2.1.3 第二运动阶段规划

第二运动阶段即为匀速运动阶段，第二运动阶段的位移s2=s-s1-s3

若s2≤0，则不进行本次重新规划，返回原规划状态；若s2>0，可以得到第二运动阶段的时间量：

(17)

2.2 先减速再减速规划

2.2.1 第一运动阶段规划

与2.1中的规划结构相似，先减速再减速规划的第一运动阶段运动过程约束条件为：

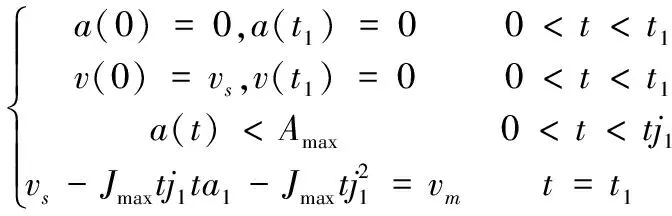
其中，t1=2tj1+ta1。

与先加速再减速中规划方法类似，考虑速度、加速度约束方程和效率最优原则可以计算得到tj1和ta1。

根据积分条件，可以计算出第一运动阶段的位移为：

2.2.2 第三运动阶段规划

第三运动的运动过程约束条件为：

其中，t2=2tj1+ta1+tv。

与先加速再减速中规划方法类似，考虑速度、加速度约束方程和效率最优原则可以计算得到tj2和ta2。

根据积分条件，可以计算出第一运动阶段的位移为：

2.2.3 第二运动阶段规划

第二运动阶段为匀速运动阶段，位移s2=s-s1-s3。

若s2≤0，则不进行本次重新规划，返回原规划状态；若s2>0，可以得到第二运动阶段的时间量：

至此，tj1,tj2,ta1,ta2,tv均已计算得到，本次规划轨迹可以最终确定。

如图3所示总结了本次轨迹规划的步骤流程。

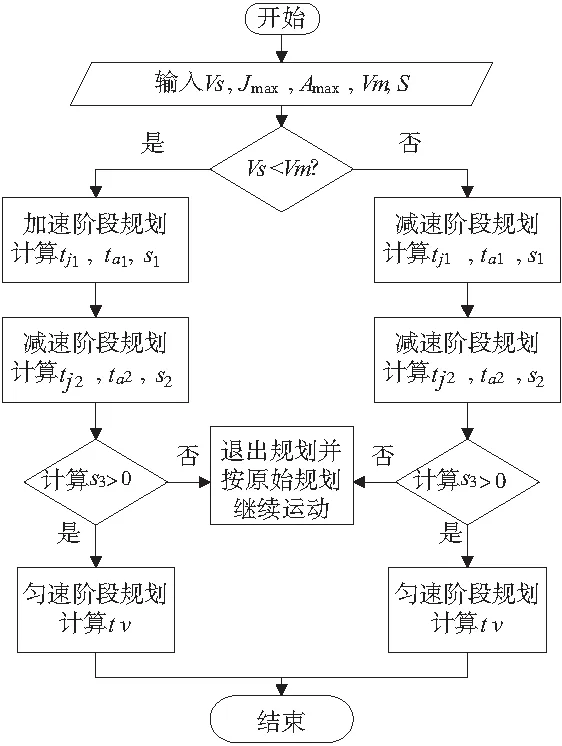
图3 轨迹规划步骤流程

3 仿真实例和分析

为验证本论文算法的运算速度,用MATLAB 进行编程仿真。给定限制条件如表1所示，仿真结果如图4、图5所示。其中，图4为原始轨迹规划，图5为进行先加速再减速的规划，图6为进行先减速再减速的规划，重新规划的起始点都取在按原始轨迹运动0.8s后开始。可以看出，在对原始轨迹规划进行重新规划后，运动轨迹依然能够完成指定位移。

表1 各状态约束参数

图4 原始轨迹规划

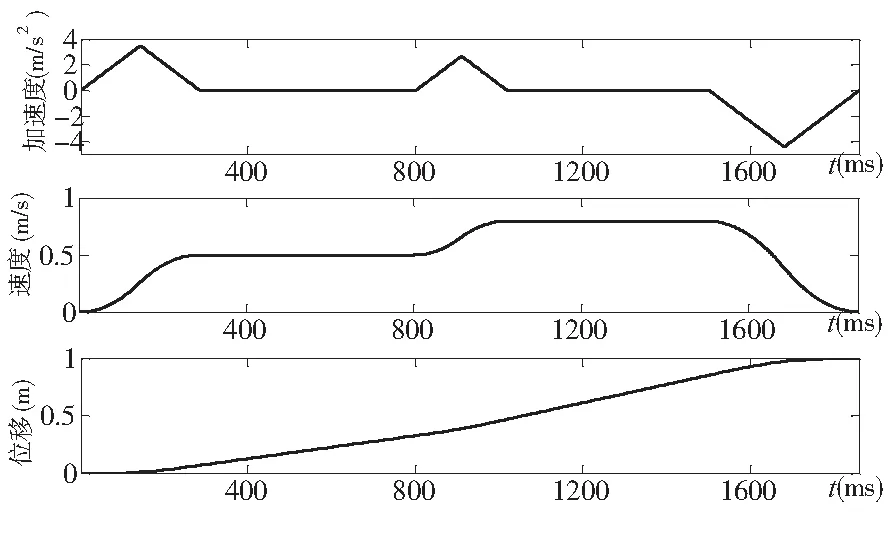
图5 先加速再减速轨迹规划

图6 先减速再减速轨迹规划

根据图3所示的规划流程，本次实验分别进行了先加速再减速情况和先减速再减速情况的仿真。而文献[10]采用的基于迭代法求解时间量的规划方法，只能进行先加速再减速的规划，具有一定的局限性。由第2节的算法分析中可以看出算法中所涉及的时间量的求解均通过公式计算得到，在计算机中所花费的运算时间极短。而文献[10]中应用迭代法求解时间量，由于迭代次数未知，重新规划所花费的时间也不确定，对于在运动过程中进行实时规划的环境中，容易造成精度损失。

4 结束语

本方法分析了一种可在匀速运动过程中进行重新规划的轨迹规划方法，实现了在运动中进行先加速再减速或先减速再减速重新规划的灵活调控， 满足了对速度变化频繁需求的同时保证运行位移不变。

本方法规划计算复杂度低，思路明确，具有较好的通用性。且本方法改善了迭代法求解时间量时时间不确定的缺点，规划计算速度快，具有极高的实时性，适用于运动过程中的实时规划。

在规划条件上，本方法须满足起始规划点在匀速段的条件，且重新规划后的轨迹必定存在匀速阶段。若要满足在运动中任意一点进行重新规划，则在重新规划时必须读取起始点的各状态初始值作为边界条件进行规划。