切削刃钝圆半径对切屑分离过程影响的有限元分析*

戴煜宸，黄健萌，赖联锋

(1.福州大学 机械工程及自动化学院，福州 350116；2.宁德师范学院 物理与电气工程系， 福建 宁德 352100)

0 引言

零件的加工过程是一个对材料表面和近表面特性的改变过程，这一过程中最关心的不是整体材料特性，而是材料近表面(或亚表面)的响应特性。在微细切削加工中，切削厚度和刀具的钝圆半径处在同一个量级下，随着切削厚度与钝圆半径比值的减小，切削刃变得不再锋利，使得“切削”逐渐转变成“犁耕”[1-2]，从而使得工-屑分离过程发生本质性的变化[3-6]，这直接影响着整个加工特性。

由于刀具切削刃钝圆的存在，使得切削加工过程中存在一个临界的切削厚度，仅当切削厚度大于该厚度时，才能保证工件表面得到较高的精度[7]，研究显示[8-10]，在微纳尺度的切削中，最小切削厚度(a)与切削刃的钝圆半径(r)存在一定的比例关系，其比值在0.1的量级上，并且介于0.05～0.4之间；在达到最小切削厚度后，材料中的一部分从大块材料中分离形成切屑，这个分离过程被视为与流体的流动具有相同的性质[11-14]，材料在流动形成切屑的过程中，存在一个切屑流动停止的分流点[15]，分流点与切削刃钝圆半径的圆心形成了对应的分流角θ，Basuray[16]在铣削研究中考虑了刀具的钝圆半径，并通过能量的耗散形式推导了θ的理论值为37.6°，其后在铣削铝、铅、低碳钢的实验中，得到分流角在28°～33°之间，论文中阐述了分流角θ与切屑的分离过程的密切关系。因此，要深入研究微切削中切屑的形成机理就需要从材料的流动性上确定切削刃钝圆对切屑分离过程的影响。

目前对于分流点的形成尚未有明确的判据，而切削刃钝圆半径对切屑的分离过程的影响也鲜有研究。本中通过分析切削过程中工件切削表层材料流动方向，提出一种判定工-屑分离点方法，在此基础上，建立二维正交切削模型，直观地观察到了切屑的分离过程，研究切削刃钝圆半径对分流点和切屑分离过程的影响。

1 切削模型的建立

1.1 本构模型

Johnson-Cook本构模型描述了金属材料从低应变率到高应变率、大应变以及考虑温度效应下的动态行为，同时还可以应用于不同晶体结构的材料，此外模型的物理参数较少，研究的人员较多，材料的参数较易得到，因此在金属切削仿真计算中得到了广泛应用，其具体表达式如下[17-18]：

(1)

(2)

表1 AISI52100 的J-C本构参数

1.2 切屑产生的判断

根据Woon[14]和Basuray[16]的论述，提出一种判定切屑产生的方法：根据材料的位移矢量判断材料的流动方向，进而判断出是否产生了切屑。图1表示的是切屑产生过程中工件表层材料的流动方向。图中A点为工件与切削刃钝圆的某个接触点，过该点作切削刃钝圆的切线，得到直线m；U1，U2，U3为由A点出发的三个任意方向的方向向量。

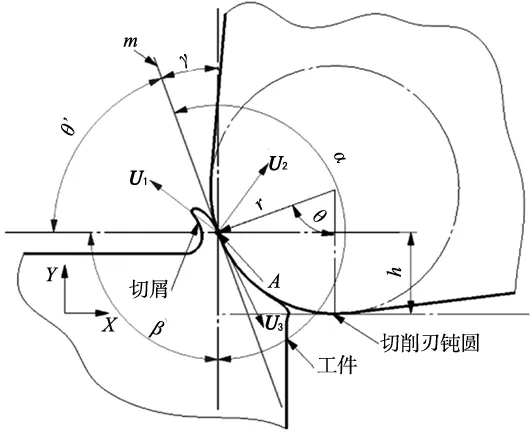
图1 工件表层材料的流动方向

当A点位移的方向向量落在θ′角内时(图1中向量U1所示)，材料的流动方向沿着X轴的负方向，由于没有切削刃钝圆的阻挡，材料可以沿着切削刃边缘向上顺利流出形成切屑。

当A点位移的方向向量落在α角内时(图1中向量U2所示)，材料流向刀具内部，但因受到切削刃的阻挡，无法顺利从钝圆上方流出，更无法流经到前刀面形成稳定切屑；材料在钝圆半径的犁耕、挤压作用下逐渐改变位移方向，此时，有可能偏向θ′角之内，汇入切屑流，也可能最终偏向Y轴的负方向(图1中向量U3所示)，沿着切削刃钝圆的曲线流向后刀面，形成已加工表面，或流回到大块材料中，被挤压在切削刃的下方。

当A点位移的方向向量落在β角内时，材料流回工件的下方或在切削刃的挤压下流向后刀面，不参与切屑的形成。

由此可知，可以根据切削的初始阶段，工件与切削刃钝圆接触区附近材料位移的方向向量判断出材料的整体流动方向，进而判断出是否形成了切屑，即：当材料的整体流动方向在θ′角之内(即不指向刀具内部)时，可以判断出此时形成了切屑，否则还未形成。

进一步地，当达到稳定切削状态后，切削刃钝圆上存在一个固定点，该点的上方，材料向上流动并能顺利流出前刀面形成切屑，在这个点之下，材料流回工件或受到切削刃的挤压形成已加工表面，这个点可确定为材料的分流点，而这个点对应的角即为分流角。假设图1中A点为分流点，则从图1中几何关系容易得出该分流角θ=θ′，对应的分流点高度h即为A点与切削刃钝圆水平切线之间的距离(如图1中所示)，由图1中几何关系可得到式(3)。

(3)

1.3 有限元模型

图2显示的是二维正交切削有限元模型。工件材料为AISI 52100(62HRC)，尺寸为120μm×40μm，其边界条件如图中所示；刀具材料为PCBN，刀具设为刚体，刀具前角为5°，后角为7°，图中REF为速度参考点，切削速度为60m/min；刀具与工件的接触行为采用库仑摩擦模型[19]。工件与刀具的单元类型为CPE4RT。

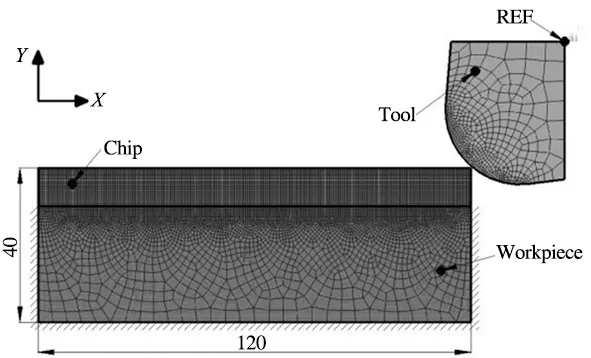
图2 二维正交切削模型

工件与刀具的材料参数、工件与刀具的接触参数等如表2所示[20-22]。

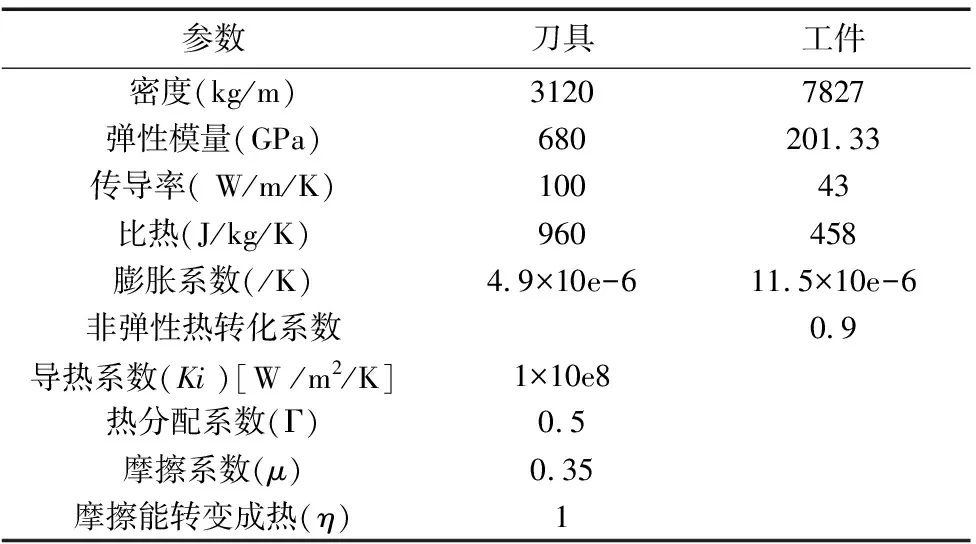
表2 二维正交切削有限元模型参数

2 结果分析与讨论

2.1 最小切削厚度

图3显示了不同切削刃钝圆半径及切削深度下材料表层的流动图。可以看出，当切削刃钝圆半径r=5μm，切削深度a=1μm时(图3a)，表层材料一部分流向后刀面和材料的下方，而另一部分则流向刀具内部，但由于切削刃钝圆的存在，这部分材料并不能完全顺利从前刀面流出，故可以判定在此切削深度下并未产生切屑。当切削深度增加到1.1μm时(图3b)，在切削的初始阶段，材料的总体流动方向即趋向于x轴负方向，且大部分都指向切削刃钝圆的外侧，能够顺利流出切削刃的钝圆形成切屑，因此，此时的切削深度可以判定为产生了切屑。由这一现象，可以推断出，当切削刃钝圆半径为5μm时，对应的最小切削厚度介于1μm与1.1μm之间，则切削厚度与钝圆半径之比a/r介于0.20～0.22之间。

由此，根据图3c、图3d可以判断出r=10μm时，最小切削厚度介于1.8μm与1.9μm之间；由图3e、图3f可以判断出r=20μm时，最小切削厚度介于4.0μm～4.1μm之间，取这两个数值的中点值确定为该条件下的最小切削厚度，即4.05μm。

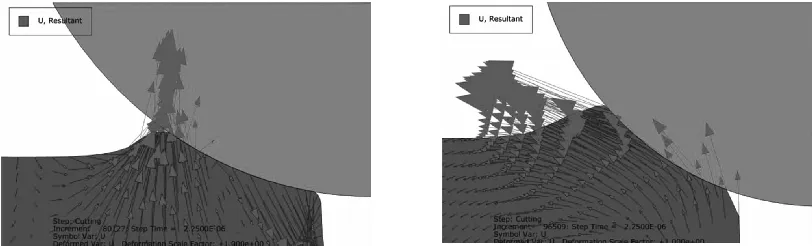
(a)r=5μm，a=1μm (b)r=5μm，a=1.1μm

(c)r=10μm，a=1.8μm (d)r=10μm，a=1.9μm

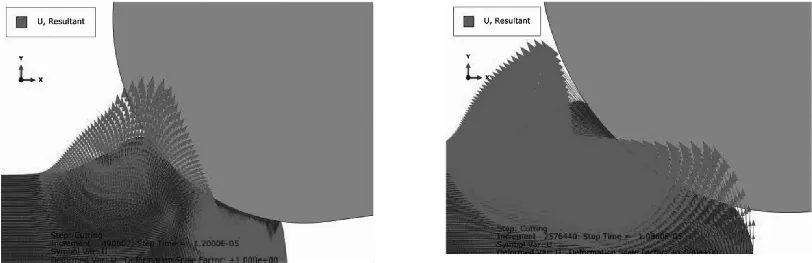
(e)r=20μm，a=4.0μm (f)r=20μm，a=4.1μm

2.2 分流点与分流角

图4为切削刃钝圆半径为5μm，切削深度为1.1μm时两个不同时刻材料的位移矢量图与云图。发现，在切深大于最小切削厚度时，材料表层的整体位移沿着刀尖钝圆的边缘向上流动(图4a)，在切屑形成前，分流点附近的材料位移大于附近区域的材料位移(图4c)，随着材料的堆积，材料的位移矢量逐渐分化为两个方向(图4b)。

图4b中位移方向向量R5_U1偏向于y轴的负方向，向量起点为P点，该点也是切削刃与工件的一个接触点，在该点往下，材料沿着切削刃钝圆朝后刀面的方向流动；向量R5_U2对应的向量起始点为Q点，从Q点往上，材料沿着切削刃的钝圆向上流动，形成切屑。当分流点产生后，分流点所在区域材料的流动速度低于其两侧区域材料的流动速度并趋于0(图4d)。从图4b，图4d还可发现，材料的分流并不是出现在某个点，而是在一个小区域中。文献[23]也指出分流点所在区域，是材料流动的一个停滞区域。

(a)材料的堆积 (b)分流点的出现

(c)材料堆积的位移云图 (d)分流点出现时的位移云图

由图4d分流点所在的区域可大致计算出分流点的高度h(取为分流点所在区域y方向的中点值)，根据式(3)可计算出对应的分流角。不同切削刃钝圆半径下最小切削厚度、分流点、分流角值具体可见表3。

表3 不同切削刃钝圆半径下最小切削厚度、分流点、分流角

根据表3中的数据可以得到图5，图5显示了切削刃钝圆半径与最小切削厚度、分流点高度的关系。

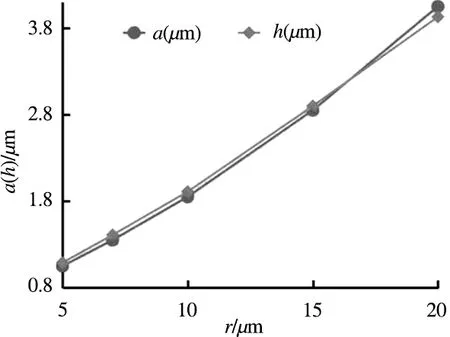
图5 切削刃钝圆半径对最小切削厚度/分流点高度的影响

从表3中可以看出，最小切削厚度a与切削刃钝圆半径r的比值介于0.19～0.21之间；由分流点高度计算得到的分流角介于36°～38.5°之间，这与文献[16]中通过理论计算得到的37.6°非常接近。从图5可以看出，分流点高度h与最小切削厚度a的值几乎重合在一起，两者都随着切削刃钝圆半径的增大而近似地线性增大。由于分流点附近材料停滞流动，即分流点附近由切向力与法向力引起的应力相等[15]，当不考虑表面黏着等作用的影响时，分流点附近的流动应力主要取决于切削刃钝圆与工件材料的接触特性，即此时分流角不随切削刃钝圆半径的变化而变化，由式(3)可得：h=[1-(tanθ+1)-0.5]·r，当分流角θ恒定时，分流点高度h随切削刃钝圆半径r线性增大。

2.3 切削力

表4是不同切削刃钝圆半径下的主切削力Fc和切深抗力Fp的值，图6是其相应的变化趋势。可以看出，Fc和Fp都随着切削刃钝圆半径的减小而减小，而随着切削刃钝圆半径的减小，Fc与Fp的值逐渐接近，介于0.81～0.91之间，这与文献[24-25]所得的结果相近，文献[24]在利用钝圆半径为30μm的刀具切削3J33合金，切削深度为21μm时，得到Fc/Fp的值为0.81；文献[25]Shimada通过分子动力学模拟，得到切削刃钝圆半径为1.57nm～3.14nm之间时，Fc与Fp的比值介于0.91～0.94之间。当进入到稳定切削过程后，随着切削刃钝圆半径的减小，单位圆弧上的切削力逐渐增大，这主要是由于当切削的深度小于切削刃钝圆半径时，切屑的形成主要来源于切削刃钝圆半径在向前运动的过程中对工件材料的挤压作用，即犁耕过程代替了切削过程。

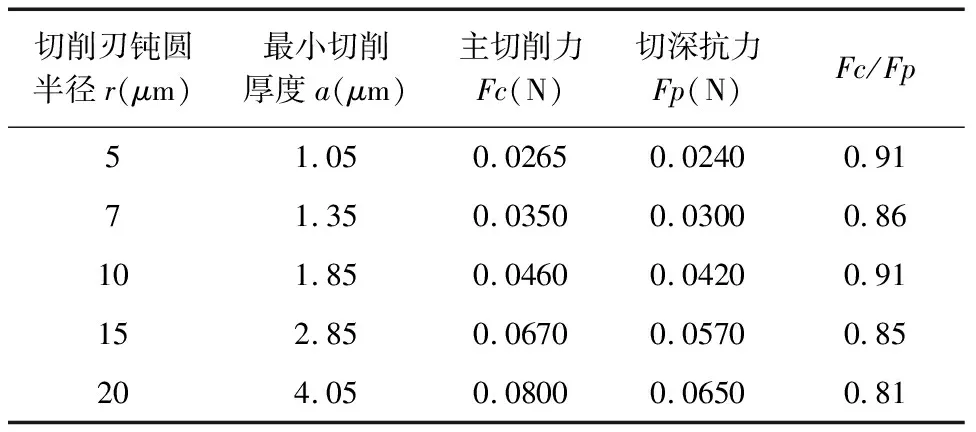
表4 不同切削刃钝圆半径下切削力

图6 切削刃钝圆半径对切削力的影响

2.4 应力分布

图7是切削刃钝圆半径为5μm，切削深度为1.1μm时切削刃钝圆附近材料的Von Mises应力云图。从图中可以看出，分流点所在区域的应力值小于其两侧区域的应力值，而应力最大的区域发生在分流点下方，即材料在该处的塑性变形最大，并且延伸到切削层的主变形区，剪切破坏首先发生在这个区域，这也说明了切屑与工件分离的位置位于分流点所在区域的下方，即切削刃钝圆与工件材料水平相切处。

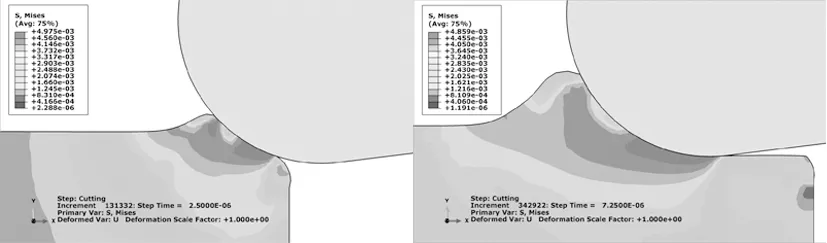
(a)分流点形成初期 (b)进入稳定切削后

3 结论

(1)切屑形成的过程中，需经过一个短暂的材料堆积过程，当材料堆积的高度高于分流点时，切屑即开始形成；

(2)最小切削厚度、分流点的高度与切削刃钝圆半径近似地成线性关系；

(3)随着切削刃钝圆半径的减小，单位圆弧上的切削力逐渐增大；

(4)分流点附近的塑性变形要小于其周围区域，材料的剪切破坏主要发生在切削刃钝圆与后刀面连接的附近区域。