HF电波多跳传播分析*

刘金鑫，陈夏霖，周佶昊，吴 磊

（重庆邮电大学，重庆 400065）

0 引 言

1 损耗分析

通俗而言，通信是信息的时空转移，考虑的指标是信息传输的可靠性和有效性。HF频段非常适合于通过电离层和地球外多重反射进行远距离传输[1]，广泛适用于军事、民用领域，在我军超视距通信领域、应急通信和船舶通信等方面已取得了长足的发展和使用[2]。本文从射线追踪法的理论出发，研究了HF传播在各传输阶段的损耗，并建立了HF多跳传输模型。

一般情况下，HF信号发射经过地球外电离层的反射回到地球，然后在地球表面产生二次反射。在能量足够的情况下，二次反射的信号仍然可以反射回电离层，依次往复，实现多次跳跃使信号传输得更远。整个通信过程中，包括自由空间传播损耗[L0]、电离层吸收损耗[La]、地球表面反射损耗[Lg]以及额外系统损耗[Lp]。其中，地球表面损耗包括固有损耗[L'g]和附加损耗[L''g]，有：

1.1 自由空间传播损耗

根据电磁场理论，全向天线功率向四周发射信号，接收端仅可能接收到部分发射信号功率。传播损耗同电磁波的频率、传播距离有关，计算公式为：

式中，d为传播距离，f为信号频率。

1.2 电离层吸收损耗

电离层中包含大量的等离子体。电磁波穿过时波的电矢量引起电子运动，电子同其他粒子发生碰撞，部分能量转移到中性分子，最终变成热能，从而引起电波振幅的吸收衰减[3]。电离层吸收包括偏移吸收和非偏移吸收[1]。相对来说，非偏移吸收远大于偏移吸收，是讨论分析的重点。

文献[4]为解射线方程而设计了一种计算电离层等离子体参数一阶偏导数的方法，在部分层的交点处一阶偏导数不连续，会造成射线的虚假反射。文献[5]研究了一种利用数字跟踪技术求解短波在电离层传播轨迹的方法，但文中是基于单层模式的简化考虑，对电离层多层模式中传播无法进行仿真分析。对HF通信，[La]主要是电波穿过电离层由D层、E层引起的吸收损耗，计算公式[1]为：

其中，e为电子电量；m为电子质量；υ为碰撞频率（υ表示一个电子在1 s内与中性分子的平均碰撞次数）；εr为等效相对介电常数；σ为等效电导率。

对于式（3），难以确定高度同电离层电子密度定性的函数关系式，故通过数值分析的方法将连续过程离散化，利用射线追踪理论，根据电离层电子密度随高度的定量关系（如图1所示），通过迭代分析判断电磁波的折射情况，并计算电离层的吸收损耗。

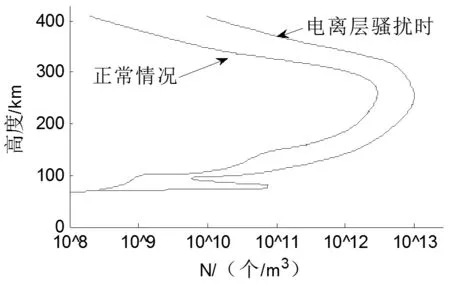
图1 电离层电子密度同高度变化

如图2所示，将地球的电离层分成薄片，每层认为是均匀的。到263 km时，薄层的折射率随高度的增加而减小，则电磁信号为一条向下弯曲的曲线。

图2 电磁波在电离层正折射

因此，可将连续变化的过程离散化，则吸收损耗转化为：

式中，αn为电离层衰减常数，dn为离散量化高度步长。

1.3 地球表面反射损耗

HF信号经过地球电离层反射到地球表面后，由于地面尺寸远大于高频电磁波波长，故会产生镜面反射，存在反射损耗[Lg]。它与电波的极化、频率、射线仰角以及地质情况等因素有关。由于电波经电离层反射后极化面旋转且随机变化，入射地面时的电波是杂乱无章的。因此，严格计算[Lg]值是困难的[1]，故选择按照圆极化波进行计算。

假设入射电波是圆极化波，即水平极化分量和垂直极化分量相等，则地面反射固有损耗为：

式中，RV和RH分别是垂直极化和水平极化的地面反射系数：

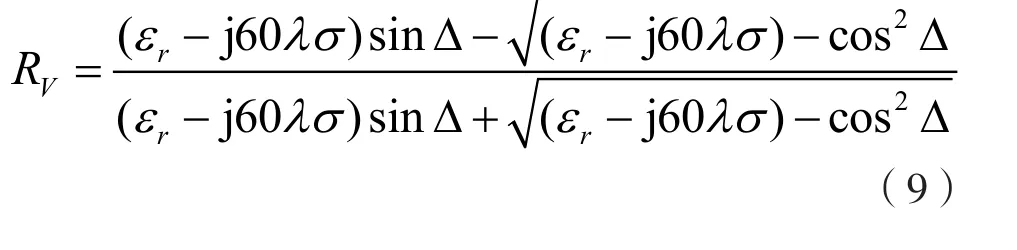
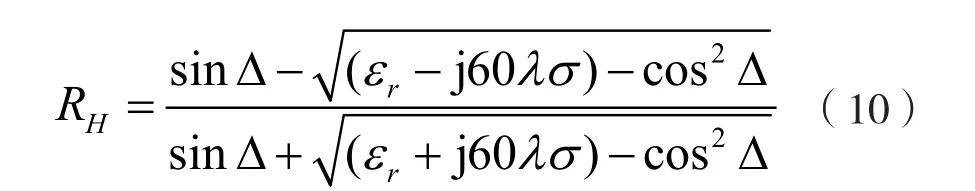
式中，Δ为射线仰角，εr为反射面的相对介电常数，σ为反射面的电导率。

对于地球表面地址情况，主要分为海洋和陆地。由于海浪的波动、山地的起伏，导致部分电磁波反射被阻挡，或者沿着电磁信号来向反射。在不考虑环球回波的情况下，认为这两种情况下的电磁信号是无效的。定义反射有效系数λ为：

其中，S0为有效反射区域面积，S为总反射考察区域面积，即由于反射遮挡问题，存在地面反射附加损耗：

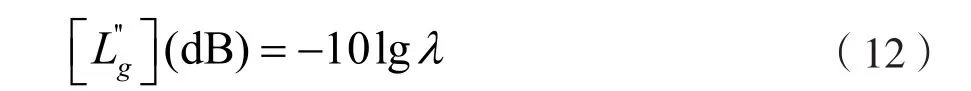
故此，总地面反射损耗为：

1.4 额外系统损耗

额外系统损耗[Lp]包括除了上述3种损耗以外的其他所有原因引起的损耗，如偏移吸收、ES层附加损耗、极化损耗、电离层非镜面反射损耗等[1]。[Lp]是一项综合估算值，一般通过大量的电路实测数据扣除上面指明的3种损耗而得到。[Lp]值与反射点的本地时间T（小时）有关，可按下述数值估算：

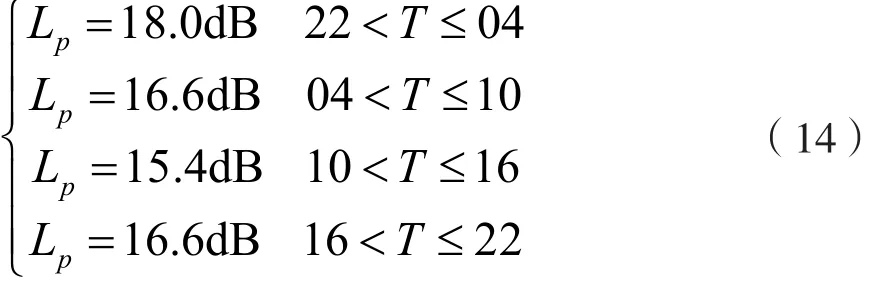
2 仿真分析

2.1 电离层

当不考虑地磁场影响时，电离层等效相对介 电 常 数 为 一 标 量 εr， 将 m=9.106×10-31kg，e=1.602×10-19C，代入式（7）中进行仿真，得到发射频率同电磁波可有效折射回地面的最大仰角关系，如图3所示。

正常情况下，选择电波频率、发射仰角为（5 MHz，60°）、（10 MHz，60°）、（15 MHz，60°）、（20 MHz，30°）、（25 MHz，30°）的5组初始条件，电波射线的仿真轨迹如图4所示。

图3 不同频率下电磁波能折射回地球的最大仰角

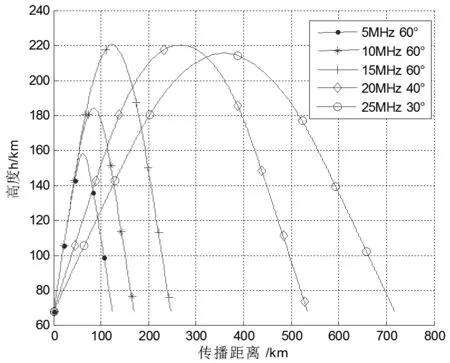
图4 电离层仿真轨迹

2.2 地球表面

地球表面海洋和陆地地型差异大，现对其分别进行仿真分析。

2.2.1 海洋反射损耗

对于HF电磁波，海水中等效相对介电常数εr=80，等效电导率σ=4.0 S/m[6]。由式（8），海洋表面反射固有损耗同射线仰角Δ的变化如图5所示。

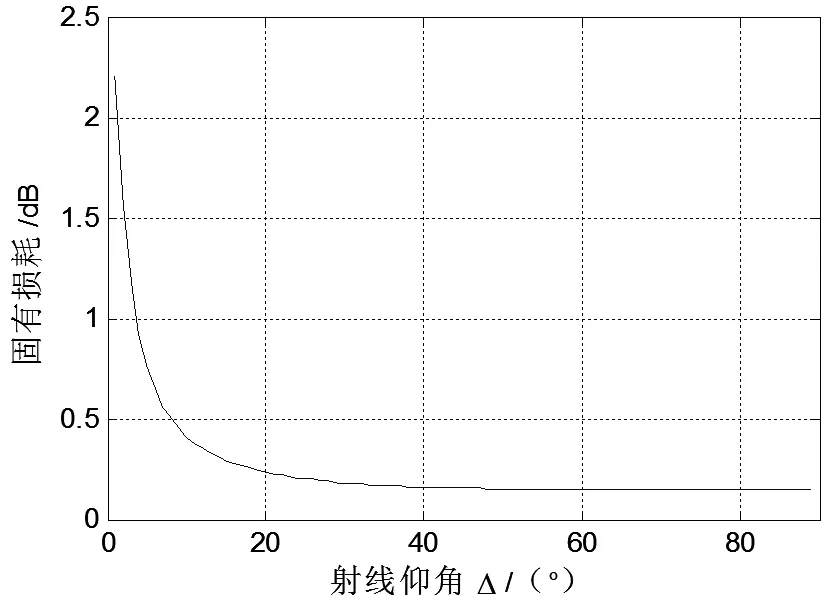
图5 海洋固有损耗同射线仰角变化

图6 水波仿真

由于波的来向无法确定，故选择4×256×256束电磁波波从4个方向进行蒙特卡洛仿真，并由式（12）得到附加损耗同射线仰角Δ的变化，如图7所示。

图7 海洋附加损耗射线仰角变化

2.2.2 陆地反射损耗

对于陆地表面，由于空气、植被和土壤的电阻率都远大于1，故取陆地表面的电导率σ为0。但是，由于地型地貌的因素，导致陆地表面的介电常数波动很大。可以将陆地看做植物和空气的混合体，给出各部分的介电常数和体积含量，即可确立等效节点常数模型[8]。

植被由植被体、自由水和结合水三部分构成，根据各部分的介电常数，采用植被的Debye-Code双频散模型[8]，即可得到植被的介电常数εc，计算公式见文献[9]。得到植被等效节点常数后，根据植被和空气的体积含量，计算陆地的等效介电常数。采用两相混合物折射模型[10]，即可得到陆地表面的等效介电常数：

式中，ευ为植被的介电常数，vυ为植被的体积含量。

取植物体的重量含水量为50%，干植物体密度为0.5×103kg/m3，自由水盐度为10%，植物体积含量50%，得到陆地表面等效介电常数εr为1.49，且在高频信号下介电常数存在0.03的变化。由式（8）可知，大地表面反射固有损耗同射线仰角Δ的变化如图8所示。

图8 大地固有损耗同射线仰角变化

图9 大地附加损耗同射线仰角变化

2.3 多跳传播仿真

设天线最大辐射方向仰角为45°，增益为20 dB，频率为15 MHz，时间为12 h，对重庆、上海、拉萨、海洋（采用2.2.1节所模拟的海浪）在正常情况下进行模拟仿真。接收端收到的信号允许的最大衰减为150 dB，仿真得到电波轨迹如图10所示。

图10 不同地型多跳仿真轨迹

结果表明，重庆、上海和拉萨地区烦人信号跳数均可达到2跳，其传播距离均未超过1 000 km；海洋跳数达到4跳，传播距离可达2 000 km。进一步发现，当存在电离层骚扰时，重庆、拉萨和上海地区的传播距离将扩大400 km左右，海洋跳数将变为5跳，距离达到3 600 km。

3 结 语

本文利用射线追踪法对HF电波传输轨迹进行仿真分析，确立了多跳传输过程中路径损耗、电离层吸收损耗、大地表面反射损耗同电磁信号射线仰角的变化关系，最后分析了4种地型情况下的跳数。后续的工作可以考虑：①若条件允许，可对仿真结果进行实际测试对比分析；②进一步提高算法的精确度；③对地面反射分析过程中，可考虑不同地型的植被类型。