钢弹簧浮置板动力吸振器设计

林龙锋，周 力

（1. 广州地铁设计研究院，广州 510000；2. 同济大学铁道与城市轨道交通研究院，上海 201804）

在地铁运行过程中，1由于轨道几何不平顺、刚度不平顺、车轮踏面磨损等因素，车轮和钢轨之间会发生动力作用，产生振动，使得车轮和钢轨的磨损加剧，又进一步加大了轮轨间的振动，形成恶性循环。同时，轮轨间的振动会向道床、隧道、土壤和周围建筑物传播，给地铁沿线居民的生活和工作带来不利影响。这些因素大大制约了地铁的建设和发展。

轮轨间相互作用产生的振动是不可避免的，那么，为了降低地铁振动对沿线居民和建筑的影响，国内外研制和开发了各种轨道减振产品，如减振扣件、梯形轨枕、钢弹簧浮置板等。其中，钢弹簧浮置板是目前效果比较好的减振产品之一[1-4]。钢弹簧浮置板的工作原理主要是通过低刚度的弹簧阻尼器，把振源（轮轨）与隧道壁隔开，进而减小隧道壁向外界环境传播的振动，达到保护沿线建筑物和居民的目的。现有研究表明，钢弹簧浮置板在降低隧道壁振动的同时，往往会增大道床和钢轨的振动，加剧轮轨间的相互作用，进一步恶化车轮和钢轨接触面，对轨道线路和车辆十分不利[5-6]。

为了解决这一问题，笔者研究通过在浮置板轨道上加设动力吸振器，降低由隔振所引发的浮置板轨道道床和钢轨振动增大的部分。动力吸振器的工作原理主要是借助吸振器的阻尼和刚度元件，通过自身振动，从目标系统中吸收能量并进行消耗，从而降低目标系统的振动。目前，国内外已经有很多关于动力吸振器在工程中的研究与应用[7-8]，在城市轨道交通行业主要应用于钢轨，而在浮置板上应用较少。将单自由度动力吸振器设计理论和多模态控制理论相结合，根据有限元模型中车辆运行状态下浮置板轨道振动频谱特性，对浮置板动力吸振器的参数进行优化设计，并分析了浮置板动力吸振器的制振效果。

1 动力吸振器设计理论与方法

1.1 单自由度主振系统的动力吸振器设计

对于一个单自由度无阻尼主振系统，根据定点扩展理论[9]，其附加的动力吸振器设计参数如式（1）～（3）所示，其中，m、k、c分别为动力吸振器的质量、刚度和阻尼，μ 为动力吸振器的质量比，M、K为主振系统的质量和刚度。

当动力吸振器处于最优设计条件时，即满足最优同调条件和最优阻尼条件，主振系统的最大振幅比由式（4）决定。由式（1）～（4）看出，动力吸振器的参数和主振系统的最大振幅比均由动力吸振器的质量比参数决定。增加质量比可以提高制振的效果，但会使整体结构变重。为了避免增加过大的质量，一般质量比不大于0.2。

文献[10]给出了单自由度无阻尼主振系统附加了满足最优设计条件的动力吸振器后的强迫振动最大振幅比近似值：

其中，eqζ是与最优状态的动力吸振器等价的单自由度系统的阻尼比。利用式（6）可以确定为了达到期望的减振效果所需的动力吸振器的质量比。

1.2 多自由度主振系统的动力吸振器设计

对于单自由度主振系统，可以通过定点扩展理论较为简单地计算出动力吸振器的参数。但现实中，主振系统往往是多自由度系统，且各自由度之间相互耦合，很难通过系统的频响函数直接求得动力吸振器的最优同调条件和最优阻尼条件。这时，首先需要利用坐标转换将多自由度系统解耦，转换成多个互不干涉的单自由度系统，然后利用单自由度系统动力吸振器的设计方法进行设计。文献[10]认为可以将以单自由度为对象的动力吸振器的最优设计法与模态控制理论相结合，即以各个模态为控制对象，将单自由度动力吸振器的最优设计关系式应用到第i阶模态的制振中。在第i阶模态动力吸振器的设置位置，通过该点的等价质量确定吸振器的质量比后，根据单自由度系统吸振器设计中的最优同调和最优阻尼条件，确定用于对第i阶模态制振的动力吸振器的参数。

1.3 浮置板轨道动力吸振器的参数设计步骤

根据2.2节中对多自由度多模态控制的动力吸振器设计方法的阐述，本文对浮置板轨道中道床板的制振设计主要按照以下3个步骤：1）根据车辆—轨道动力学原理，建立车辆—浮置板轨道有限元模型，计算出车辆运行过程中浮置板的动力响应；2）对浮置板进行模态分析，结合浮置板动力响应的频谱特性，确定需要制振的模态阶数以及吸振器的安装位置；3）将单自由度吸振器设计原理与多模态控制相结合，计算出动力吸振器的参数。

2 钢弹簧浮置板动力吸振器设计

2.1 车辆—轨道动力耦合有限元模型仿真与计算

本文利用ABAQUS有限元软件，根据图1所示的车辆—轨道简化模型，建立车辆—钢弹簧浮置板轨道有限元模型。其中，车体和转向架均采用刚体，质量及转动惯量均按照地铁B型车辆参数进行设置；一系和二系悬挂用弹簧阻尼单元进行模拟；浮置板轨道扣件刚度为50 kN/mm；浮置板采用6 m板，钢弹簧套筒间距1.2 m，钢弹簧的刚度大小设置为6.9 kN/mm。

图1 车辆—轨道动力模型Fig. 1 Vehicle-track dynamic model

本文主要关注浮置板垂向振动，选择美国六级谱作为系统的激励，把轨道不平顺看作平稳随机过程，采用三角级数法，将高低不平顺谱转换为轨道高低不平顺空间样本[11]，图2、图3为在轨道高低不平顺激励下，车辆运行过程中的浮置板振动加速度的计算结果。

图2 钢弹簧浮置板中点振动时程曲线Fig. 2 Time history curve of mid-point on the steel-spring floating slab

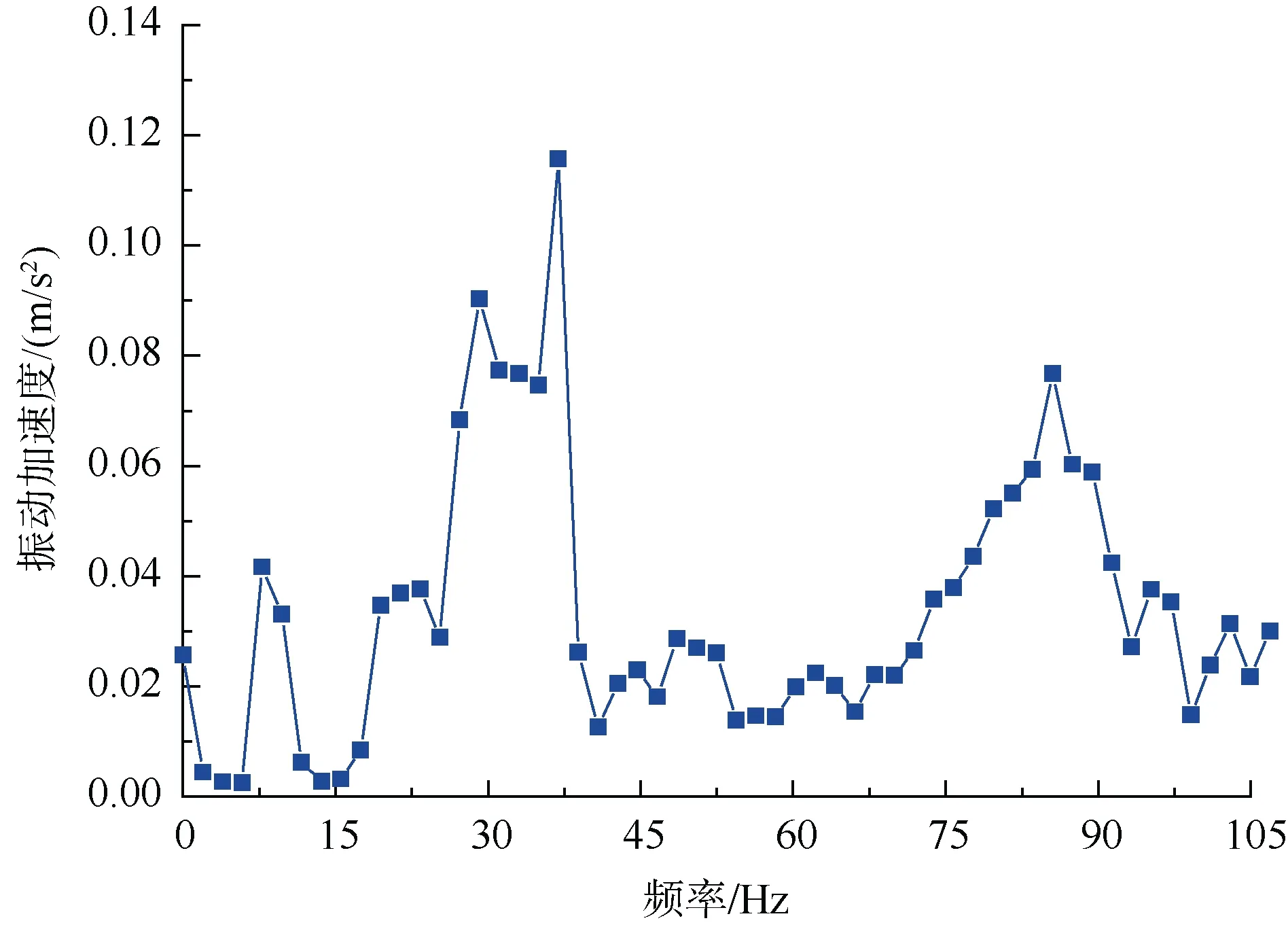
图3 钢弹簧浮置板中点振动频域Fig. 3 Vibration frequency curve of mid-point on the steel-spring floating slab

2.2 浮置板模态计算

由于本文主要关注浮置板垂向振动，所以所求的浮置板模态也是垂向的。利用ABAQUS有限元软件，建立浮置板实体模型，采用Lanczos算法，求出浮置板前四阶模态，如图4所示。

图4 浮置板前四阶模态Fig. 4 First four modes of the floating slab

从2.1节图3中可以看出，在100 Hz以内，钢弹簧浮置板在37 Hz和85 Hz附近有较大的振动峰值，浮置板在这两处各有一阶模态（第2阶模态和第3阶模态）。因而，本文以浮置板的第2、3阶模态为控制对象，通过设置相应的动力吸振器来控制浮置板在37 Hz和85 Hz附近的振动。

2.3 浮置板动力吸振器参数计算

根据多模态动力吸振器的设计方法，在将多自由度系统转化为N个互不耦合的单自由度系统后，可以把系统各个模态视为控制对象，将单自由度动力吸振器的最优设计关系式，即公式（1）～（5）应用到第i阶模态的制振中。在确定了第i阶模态的等价阻尼后，如果能够获得第i阶模态的系统等价质量Mi，就可以计算出第i阶模态动力吸振器的设计参数。系统的第i阶模态的等价质量与吸振器的设置位置有关。具体来说，首先借助ABAQUS有限元软件，采用Lanczos方法进行模态分析，得到第i阶模态的一致惯性质量，并结合安装位置的振幅与最大振幅的关系，计算得到等价质量；其次，在确定吸振器阻尼后，根据多模态控制与动力吸振器设计理论[10]，结合单自由度动力吸振器的最优参数设计，从而计算出第i阶模态的吸振器参数。

吸振器的设计质量大小与吸振器控制的目标模态阶数以及安置的位置有关。考虑到如果吸振器设计质量过大，兼顾到浮置板轨道空间布局，在实际应用中不便于实现，所以本文尽量将动力吸振器设置在所控制的模态振动较大处。因而，本文将抑制第2阶模态振动的动力吸振器 1安置在浮置板沿轨道纵向端部（两端各一个），即第2阶振动模态波腹位置（变形最大处）；将抑制第3阶模态振动的动力吸振器2安置在浮置板轨道外侧的中部位置（左右两侧各一个），即第3阶振动模态波腹位置，如图5所示。同时，动力吸振器1的安置位置恰好是浮置板第3阶振动模态的波节位置，动力吸振器2安置位置恰好是浮置板第2节阶振动模态的波节位置，实现了各个模态的非耦合控制设计，避免了抑制不同模态振动的动力吸振器之间相互干扰。表1给出了控制各模态振动的动力吸振器最优参数。

虽然在参数计算过程中，模型的质量是按照相应模态最大振幅点处对应的质量大小而设计，但考虑到实际情况，选择具有一定体积的实体模型，结合轨道的空间、车辆运行安全等因素，动力吸振器1和2的质量块几何尺寸初步设置为1 m×1 m×0.1 m、0.6 m×0.4 m× 0.1 m。此外，质量块通过弹簧/阻尼矩阵与浮置板相连，方向与板面垂直，弹簧/阻尼矩阵的总刚度和阻尼大小分别等于表1中对应的刚度和阻尼参数值。

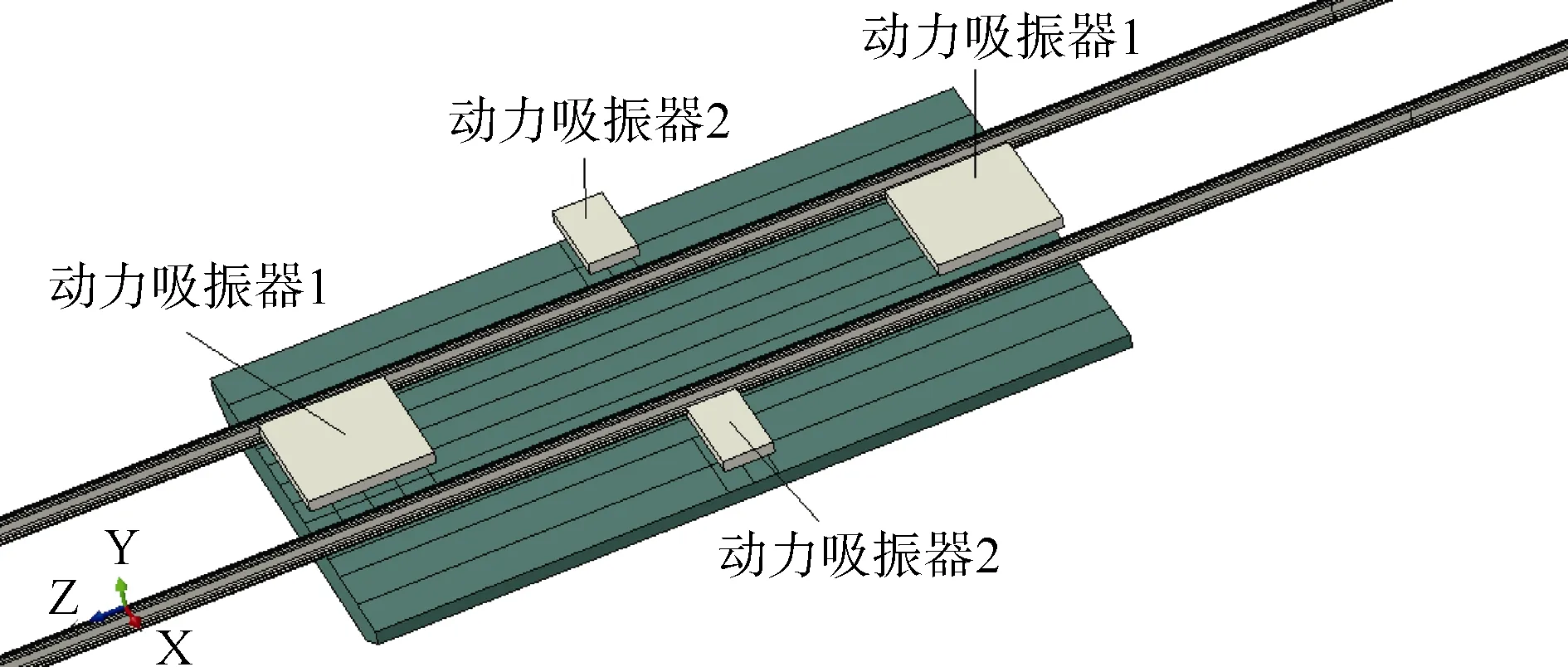
图5 动力吸振器位置分布Fig. 5 Position distribution diagram of the dynamic vibration absorber

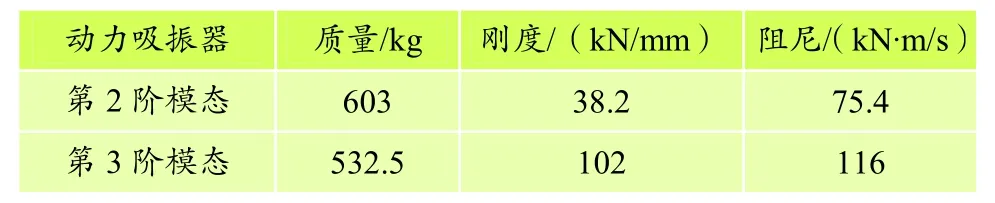
表1 控制各模态振动的动力吸振器最优参数Tab. 1 Optimal parameters of the dynamic vibration absorber for controlling the modal vibration

2.4 动力吸振器吸振特性分析

如图6所示，将动力吸振器（DVA）设置在车辆—浮置板轨道有限元模型中，计算浮置板轨道在车辆载荷作用下的动力响应。其中，动力吸振器采用实体单元进行模拟，吸振器的刚度和阻尼用线性弹簧/阻尼单元矩阵表示。将设置有吸振器的浮置板道床中点的动力响应时域和频域结果与未设置吸振器的浮置板道床中点的动力响应结果进行对比，如图6、图7所示。

图6 浮置板道床中点振动加速度时程Fig. 6 Vibration time history curve of acceleration at the midpoint of the floating Slab

图7 浮置板道床中点振动加速度频谱Fig. 7 Vibration frequency curve of acceleration at the midpoint of the floating slab

如图7所示，钢弹簧浮置板在加设有动力吸振器后，板中点的加速度响应明显降低。在未设置动力吸振器前，浮置板道床中点在100 Hz以内有两个峰值，分别在30～37 Hz和79～89 Hz范围内，各自对应浮置板的第2阶模态和第3阶模态，如图8所示。在加设了动力吸振器后，这两频段的振动得到明显改善，峰值分别从0.116 m/s2和0.077 m/s2降低至0.089 m/s2和0.044 m/s2，且对其他频段（100 Hz以内）的振动基本没有产生不利影响。这表明，动力吸振器有效抑制了浮置板的第2阶模态和第3阶模态的振动。此外，加设了动力吸振器后，浮置板在第四阶模态频率（103.2 Hz）附近的振动也有所降低。

浮置板上有、无设置动力吸振器时，钢轨振动响应如图 8所示。从图中可以清楚地看到在设置了动力吸振器后，钢轨的振动响应有所降低。这说明，通过在浮置板上安装动力吸振器不但能够降低道床板的振动，同时也能够使得钢轨低频范围内的振动略有减小。

图8 轨道钢轨振动加速度频谱Fig. 8 Vibration acceleration spectrum of the rail

3 结论

笔者以车辆荷载作用下的浮置板轨道为研究对象，利用建立的车辆—轨道有限元动力仿真模型，计算得到钢弹簧浮置板振动加速度响应，结合浮置板的自振特性，运用多模态控制理论，得到钢弹簧浮置板动力吸振器的设计参数，并对动力吸振器的吸振效果进行了分析，得到如下结论：

1）基于定点扩展理论，将单自由度动力吸振器设计理论和多模态控制理论应用于浮置板动力吸振器设计中，并结合浮置板轨道在车辆荷载作用下的动力响应特性与浮置板本身的振动特性，能够准确制定具有良好制振效果的动力吸振器参数。

2）在车辆荷载作用下，安装有动力吸振器的浮置板轨道道床在30～37 Hz和79～89 Hz两个频段范围内的振动加速度峰值分别降低了23%和42.8%，这说明在设计工作频段范围内，动力吸振器具有较好的吸振效果；但在设计工作频段外，动力吸振器基本没有任何效果。

3）在动力吸振器的设计工作频段范围内，不仅浮置板道床的振动明显降低，钢轨的振动也有所降低，而传统的隔振措施在降低轨道板振动的同时往往会增大轨道的振动，这是动力吸振器较为突出的优点。

质量块材料、轨道空间大小、车辆运行安全等均是影响动力吸振器几何尺寸设计的重要因素；此外，动力吸振器在工作过程中的振动相应大小也是影响吸振器参数设计的重要因素。本文并未对上述内容进行仔细研究与分析，动力吸振器的参数设计还处于理论阶段，有待进一步的研究。