考虑接头影响的盾构隧道地震响应分析
陈怀伟
(浙江省机电设计研究院有限公司,杭州 310051)
1 研究背景1
随着我国新一轮基础设施建设高潮期到来,盾构隧道凭借其施工安全快速、占地面积少、对环境影响小等优势得到了广泛应用,覆盖了交通、市政、电力、水利等多个领域[1]。与此相对应的是我国面临的严峻地震形势,地处太平洋板块和欧亚板块交汇部位使我国地震活动异常活跃,且当前正处于我国几大地震带的活跃期,工程抗震问题越发严峻[2]。从住房和城乡建设部颁发的《市政公用设施抗震设防专项论证技术要点(地下工程篇)》可看出当前工程建设中抗震问题备受关注[3]。
20世纪60~70年代,通过地震观测及振动台试验研究,研究人员逐渐认识到地下结构具有较小视比重,其地震响应特性并不取决于结构本身,而是取决于周围地层的振动特性[4]。以此理念进行抗震设计的地下结构以美国BART系统最具代表性[5],日本学者提出反应位移法并一直沿用至今,在日本国内铁道、共同沟、地下停车场等抗震设计中广泛采用[6-7]。我国近年颁布《城市轨道交通结构抗震设计规范》(GB 50909—2014)首次将反应位移法作为轨道交通地下结构的抗震设计方法[8]。国内许多学者采用反应位移法开展了研究并对其进行了实用化的改进,如刘晶波等[9]结合反应位移法的物理概念和理论基础,提出适用于复杂断面地下结构地震反应分析的整体式反应位移法;董正方等[10]采用平面弹性理论复变函数方法,推导具有小孔无限介质在无限远处受剪应力的水平位移,并将其应用于反应位移法中地层层位移的求解;宾佳等[11]在现有静力有限元求解地层弹簧系数方法的基础上,通过比较计算时不同的施力方式,对反应位移法地层弹簧系数求解方法进行改进;张景等[12]针对双跨箱形地下结构提出基于地层—结构模型施加强制位移和加速度的反应位移法简化分析途径,简化其计算过程并提高了适用性。综上可知,反应位移法历经多年发展和进化仍被广泛使用,将成为未来一段时间内隧道结构,特别是埋置于土质地层中的盾构隧道等随着地层变形的地下结构的主要抗震计算方法。
现有大部分研究成果中均将盾构隧道衬砌采用匀质圆环代替,该模型无法直观、精确地表征盾构隧道接头对整环衬砌受力及变形的影响。当需要计算错缝拼装影响时,在匀质圆环模型中须引入弯曲刚度有效率η和错缝弯矩传递率ξ,来计算整环刚度因管片接头造成的降低以及错缝拼装时环间接头的弯矩传递作用。该方法虽然简便,但系数 η、ξ的确定均需由试验确定,设计人员常凭经验取值,带有一定的主观性,地铁盾构隧道设计中通常的取值为 η=0.6~0.8、ξ=0.5~0.3[13]。考虑到接头影响的盾构隧道地震内力及变形规律如何,采用匀质圆环模型开展地震内力计算时误差大小等问题有待回答,因此,笔者分别采用匀质圆环模型以及梁—弹簧模型对某盾构隧道进行反应位移法计算,对比分析考虑和不考虑接头作用时盾构隧道地震响应的差异,为相似工程的抗震设计提供参考。
2 反应位移法原理
盾构隧道等地下结构在地震作用下最主要的振动特性为:1)隧道结构对地层振动具有依赖性和追随性;2)隧道结构的存在对地层本身的振动影响很小。反应位移法即建立在上述振动特性的基础上,其荷载组成分为三部分:结构顶底部位移差,地层作用于结构周边的剪应力以及结构的惯性力。通常而言结构惯性作用在地震内力中占比很小(不足5%),一般均做忽略处理(见图1)。确定反应位移法荷载的关键是求解自由地层位移及剪应力分布,通常根据地层实际情况可将地层结构简化为均匀地层或水平成层地层。

图1 反应位移法Fig. 1 The seismic deformation method
2.1 均匀地层
均匀地层位移分布可假定为三角函数分布(1/4余弦曲线形式),文献[8]根据此假定给出自地表向下沿土层深度方向同一时刻位移分布及剪应力计算公式:

其中,umax为场地地表最大位移;H为地表至抗震基准面的深度;Gd为地层动剪切模量。
2.2 水平成层地层
土层在深度方向上分层显现时,可将其简化为水平多层平面模型,根据一维等效线性理论建立地层位移波动方程,土体采用Maxwell黏弹性本构,并将实际地震作为输入,求解各层地层的位移及剪应力响应,计算过程一般通过计算机程序实现,其中最著名的为SHAKE程序,随着目前商用软件的成熟,该方法已经成为一种常用的计算地层位移及剪应力的方法,其计算精度较规范中的三角函数分布假定更精确,本文即采用该方法进行计算。
3 计算模型及其实现
3.1 计算模型的选择
由于盾构隧道抗震研究滞后于静力研究,因此当前盾构隧道抗震设计时仍以匀质模型为主,计算中的重要参数弯曲刚度有效率η以及弯矩传递率ξ的取值主要基于经验,带有一定的主观性。由此导致两方面的问题:首先,模型中不考虑盾构隧道接头时,对其地震内力及变形是否存在显著影响;其次,基于匀质圆环模型的计算结果精度如何评价。因此本文分别采用图2所示匀质圆环模型及梁—弹簧模型开展盾构隧道反应位移法计算,对上述问题进行研究。
图2(a)所示为一个具有均匀刚度的圆环,计算时考虑接头对整环刚度的折减;当考虑错缝拼装的影响时,以弯矩传递率系数ξ对管片的设计弯矩进行提高,对接头处的设计弯矩进行折减,调整后的弯矩分别为(1+ξ)M、(1–ξ)M。图2(b)所示3环梁—弹簧模型采用曲梁模拟盾构管片,中间为一个整幅宽环,两侧为两个半幅宽环;采用弯曲、拉压、剪切弹簧模拟环间接头,其中以弯曲弹簧起控制作用;采用剪切弹簧模拟环间螺栓的作用。使用梁—弹簧模型的优势在于可以根据管片真实拼接方式调整接头位置,从而实现考虑接头影响以及不同拼装方式下盾构隧道管片力学行为分析。

图2 匀质圆环模型及梁—弹簧模型Fig. 2 Homogeneous ring model and beam-spring model
3.2 有限元方法实现
本文数值计算的实现采用了大型通用有限元软件ANSYS,其中管片衬砌采用梁单元(beam3)模拟,环间接头以及地层切向弹簧 Kt采用线形弹簧单元(combin14)模拟;管片接头正负抗弯刚度Kθ不同,地层法向弹簧拉压刚度Kr不同,因此采用非线性弹簧(combin39)模拟,有限元模型如图3所示。进行反应位移法计算时,将地层强制位移施加于地层弹簧的末端(非结构一端),将地层剪应力转换为梁单元的节点力施加在梁单元节点上。

图3 梁—弹簧模型反应位移法计算Fig. 3 Seismic deformation method of beam-spring model
4 计算实例
4.1 工程概况
以杭州地铁2号线二期工程勾—新盾构区间为研究对象,该区间隧道采用单层装配式混凝土管片衬砌,外径6 200 mm,内径5 500 mm,管片厚度350 mm,幅宽1 200 mm,标准环采用1块封顶块(22.5°)、2块临界块(67.5°)、3块标准块(67.5°)的分块方式(见图4),管片混凝土等级为C50,整环管片采用12根M30环向螺栓以及16根M30纵向螺栓连接。因缺少动力实测参数且材料应变速率较低,因此本次计算参数均选取静力参数,管片接头处抗弯刚度Kθ正负抗弯刚度分别为 5×107kN·m/rad 及 3×107kN·m/rad,当不考虑管片环之间的错动时,环间接头的剪切刚度通常认为是无穷大,数值计算中为求收敛快速可将其设置为比管片接头刚度高若干数量级的值。按照参考文献[8]中给出的地层弹簧单元刚度取值方法,将地层基床系数与单元作用面积的乘积作为刚度值,本次计算地层法向压缩刚度Kr取为1.72×107N/m,切向拉压刚度Kt取为 5.74×106N/m。
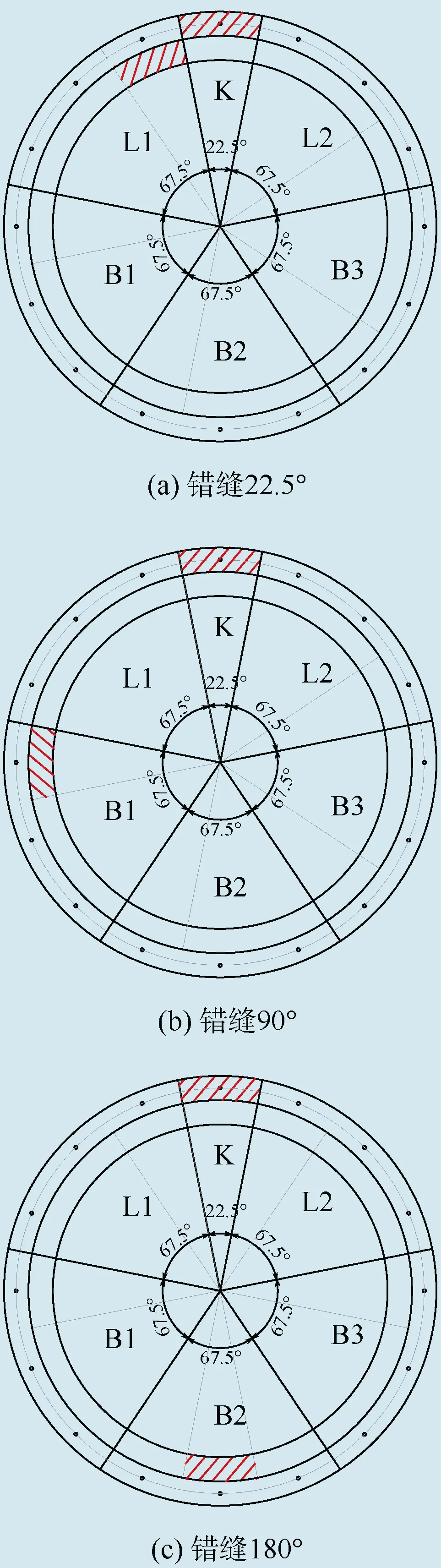
图4 管片分块Fig. 4 Segment assembling type
对3种错缝拼装方式进行计算,同时单设一组工况采用匀质圆环模型,作为梁—弹簧模型计算结果的对照,工况划分如表1所示,其中错缝拼装时,中间环封顶块位于拱顶,前后环与中间环错动某一角度,真实的匀质圆环模型中弯曲刚度有效率及弯矩传递系数取值需根据室内实验确定,本文仅取一组常用数值进行计算。

表1 工况计算Tab. 1 Calculation cases
4.2 计算断面
该区间隧道纵向穿越多种黏土、粉质黏土地层,计算中选取图5所示地层为计算断面,该断面内隧道埋深12 m,位于黏土⑤21地层中,根据规范[8]规定选取隧道底部3倍洞径处为抗震基准面,各土层的物理力学参数如表2所示。

图5 计算断面分层Fig. 5 Calculation cross section of the stratum
4.3 地震参数
根据《中国地震动参数区划图》规定,本地区设计地震动峰值加速度为0.05 g,由于本工程场地为软弱土,建筑场地类别为III类,于抗震不利,故设计文件中规定“本工程区间隧道按照7度设防烈度进行抗震验算”。因此选用本地区峰值加速度为0.1 g的人工合成地震波进行计算,地震波加速度时程如图 6所示。
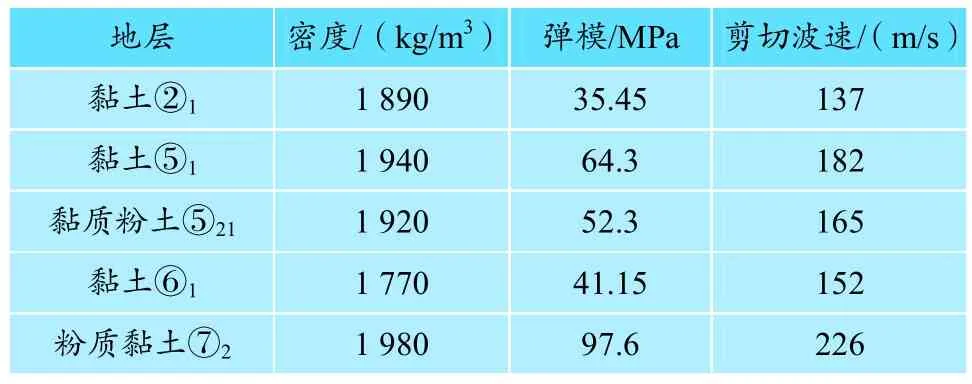
表2 地层物理力学参数Tab. 2 Physical and mechanical parameters of the stratum

图6 人工合成地震波加速度时程曲线Fig. 6 Acceleration time history of synthetic seismic waves
5 计算结果分析
5.1 地层位移及剪应力分布

图7 地层动力计算结果Fig. 7 Dynamic calculation results of the stratum
结构顶底部位移差最大时刻的地层位移峰值分布曲线及地层剪应力分布曲线如图7所示。据图可知,从抗震基准面起,随着埋深减小,地层位移峰值逐渐增大,而地层剪应力则逐渐减小。由于地层的非均匀性,地层位移及剪应力的分布曲线并非简单的线性或三角函数形式,曲线斜率与地层特性相关。该断面内结构顶底部最大位移差为0.002 8 m,此时结构顶底部地层剪应力分别为62.31 kPa和82.53 kPa。如图8所示,将地层位移差、剪应力按照结构模型中地层弹簧与模型底面的距离进行线性差值计算,并将差值后的水平位移分解在隧道外表面的法向和切向,以强制位移的形式作用于地层弹簧非结构端,剪应力可按照类似的方式差值后转化为节点力施加于结构上,从而可以求出结构最大地震内力及变形。

图8 地层强制位移施加Fig. 8 Method for the seismic deformation application
5.2 结构地震内力分析
图9 所示为匀质圆环模型地震内力计算结果。由于未考虑接头的影响,整环结构采用连续梁模型,故横断面地震内力分布连续,其中弯矩、轴力近似反对称分布,管片环共轭 45°方向上出现最大值,由于地震作用往复循环,左右拱肩、拱脚位置将交替出现弯矩、轴力最大值,且管片内外侧将交替承受拉压应力作用;从图9(b)可知工况1整环管片全断面受压,拱肩部位轴力最小,而此处弯矩最大,因而偏心距最大,为横断面内抗震最薄弱部位;断面内剪力呈近似对称分布,其对称轴相比竖直方向产生轻微偏转是由于地层法向弹簧不受拉仅受压的缘故。图10~12为3种错缝拼装方式下结构地震内力,地震内力分布规律大致相同,但由于接头的存在,内力分布与接头位置相关,对比工况1~4的弯矩分布可知,当模型中考虑了管片接头作用时,横断面弯矩在刚度较小的接头会有显著的降低,在弯矩图上表现为“内凹”,而匀质圆环模型则体现不出管片、接头之间的差异;轴力与剪力的分布则因环间接头的传力作用而发生突变,此外,拱肩、拱脚部位的轴力还有可能因接头存在而改变正负号,而这一点是匀质圆环模型中未出现的。

图9 匀质圆环模型地震内力结果Fig.9 Seismic internal force of the tunnel using the homogeneous ring model

图10 错缝22.5°拼装地震内力结果Fig. 10 Seismic internal force of the staggered assembling by 22.5°

图11 错缝90°拼装地震内力结果Fig. 11 Seismic internal force of the staggered assembling by 90°

图12 错缝180°拼装地震内力结果Fig. 12 Seismic internal force of the staggered assembling by 180°
表3所示为不同工况内力峰值统计,工况1中管片弯矩值为经弯矩传递系数(1+ξ)M修正后的结果。从表2中可看出,模型中是否考虑接头对横断面地震内力分布影响显著,具体而言,采用匀质圆环模型时,经修正的最大设计正弯矩为102.75 kN·m,错缝时最大正弯矩平均值为97.57 kN·m,二者相差5.3%,而最大负弯矩则相差 19.2%;在轴力方面,轴压最大值二者相差21.84%,但在轴力最小值方面,匀质圆环模型中轴力均为压力,但错缝拼装的梁—弹簧模型,轴力均出现了拉力,差异显著;在剪力方面,最大正、负剪力分别相差11.9%、19.1%,差别也较为明显。

表3 不同工况内力峰值Tab. 3 Peak internal force of different cases
采用梁—弹簧模型且错缝角度不同时,结构地震内力峰值也略有差别。在本文给定的计算实例中,错缝 90°拼装地震内力峰值最小,而错缝 180°时最大;就具体数值而言,弯矩、轴力、剪力分别相差20.7%、15.4%以及26.4%,而这一差异需在设计中引起重视。
5.3 结构变形分析
盾构隧道地震响应主要取决于地层的振动特性,反应位移法中的主要荷载为地层位移差以及剪应力,各工况中结构变形结果很好地印证了这一点。图 13所示为工况1结构位移矢量图,不同工况下位移矢量图形类似,仅最大数值略不相同。从图14中可知各工况中最大位移相差很小,模型中接头是否存在并不显著影响结构的最大变形量。其中最大值0.003 61 m和最小值0.003 43 m仅相差4.99%,并且其数值接近地震荷载中的地层位移差为0.002 8 m;而5.2节的分析显示管片内力差异则达到20%左右,可见地震作用下是地层位移对结构变形起到控制作用,结构自身刚度在其变形量上并未起控制作用。
5.4 接头内力及变形

图13 整环衬砌变形矢量图Fig. 13 Deformation vector diagram of tunnel ring

图14 不同工况衬砌变形最大值Fig. 14 Maximum deformation of lining in different cases

图15 中间环接头编号Fig. 15 Number of segmental joints

表4 各工况中接头弯矩及转角最大值Tab. 4 Maximum moment and rotation angle of the segmental joints
采用匀质圆环模型不能直观地求出管片接头处的内力及变形,须经弯矩传递系数(1–ξ)M修正得出弯矩后,再计算出接头处的转角。采用梁—弹簧模型可以方便地求出各接头处的地震内力及变形。图15为中间环接头编号,表 4所示为各工况管片接头弯矩、转角最大值及其位置。地震作用下,位置3、4处的接头变形最大,而这两个位置分别接近左右 45°拱脚部位,与前述内力分析中衬砌弯矩最大值分布位置吻合。匀质圆环模型得出接头最大转角分别为 1.38×10–3及–1.65×10–3rad,3 种错缝拼装时的平均值则为 7.63×10–4和–1.35× 10–3rad,匀质圆环模型较梁—弹簧模型转角计算结果分别为 44.7%及 18.2%,错缝不同角度拼装造成的转角差异最大可达8.2%,可见地震作用下虽然各工况整环变形相差不大,但接头转角计算结果却因接头的存在与否相差较大,也会因错缝角度不同而略有不同。证明考虑接头影响对盾构隧道地震动力响应主要的影响是管片内力和接头受力及转角,对整环变形影响很小。
6 结论
基于工程实例分别采用匀质圆环模型及梁—弹簧模型,考虑不同拼装方式对盾构隧道地震响应进行计算分析,得出以下结论:
1)在地震作用下,盾构隧道横断面地震弯矩、轴力为近似反对称分布,在横断面上左右拱肩、拱脚位置出现弯矩、轴力最大值,剪力分布近似对称分布,匀质圆环模型与梁—弹簧模型揭示出相同的规律,但就分布形状而言,梁—弹簧模型中的接头会导致管片内力图形在接头部位的内凹或突变。
2)计算模型中是否考虑接头影响对结构盾构隧道整环内力峰值影响显著;同时,管片错缝拼装时因错缝角度不同也会造成地震内力峰值的差异。采用本文工程实例参数计算结果显示:匀质圆环模型所得地震内力峰值与梁—弹簧模型相差约 20%,并且拱肩、拱脚部位的轴力会因接头而改变拉压性;错缝 90°拼装与错缝180°拼装时内力峰值差异也可达20%以上,可见计算盾构隧道地震内力时考虑管片接头影响的必要性。
3)地震作用下,盾构整环的变形并不随着拼装方式的变化而表现出明显的差异,匀质圆环模型、梁—弹簧模型计算所得整环变形差异不足 5%,结构整体变形接近反应位移法计算时输入的地层位移差,证明地层的变形对结构整环变形起到支配作用。
4)当采用匀质圆环模型与梁—弹簧模型时,管片接头转角在地震作用下的差异最大可达40%以上,梁—弹簧模型中不同错缝角度时的最大差异约 8%,可见计算模型中是否考虑接头以及拼装方式对管片接头转角影响较大,而匀质圆环模型受计算参数限制,当需要精确计算接头转角时不再适用。

