大型数据表格取整算法研究
刘杰
1 引言
通信工程的设计由说明、图纸和预算共三部分组成,其中预算要求每个站点做一个,预算金额保留两位小数,并提供预算汇总表。预算汇总表样式如表1所示,其中灰色填充部分为小计项和合计项(下称“和项”),无颜色填充部分为单项材料金额(下称“细项”)。
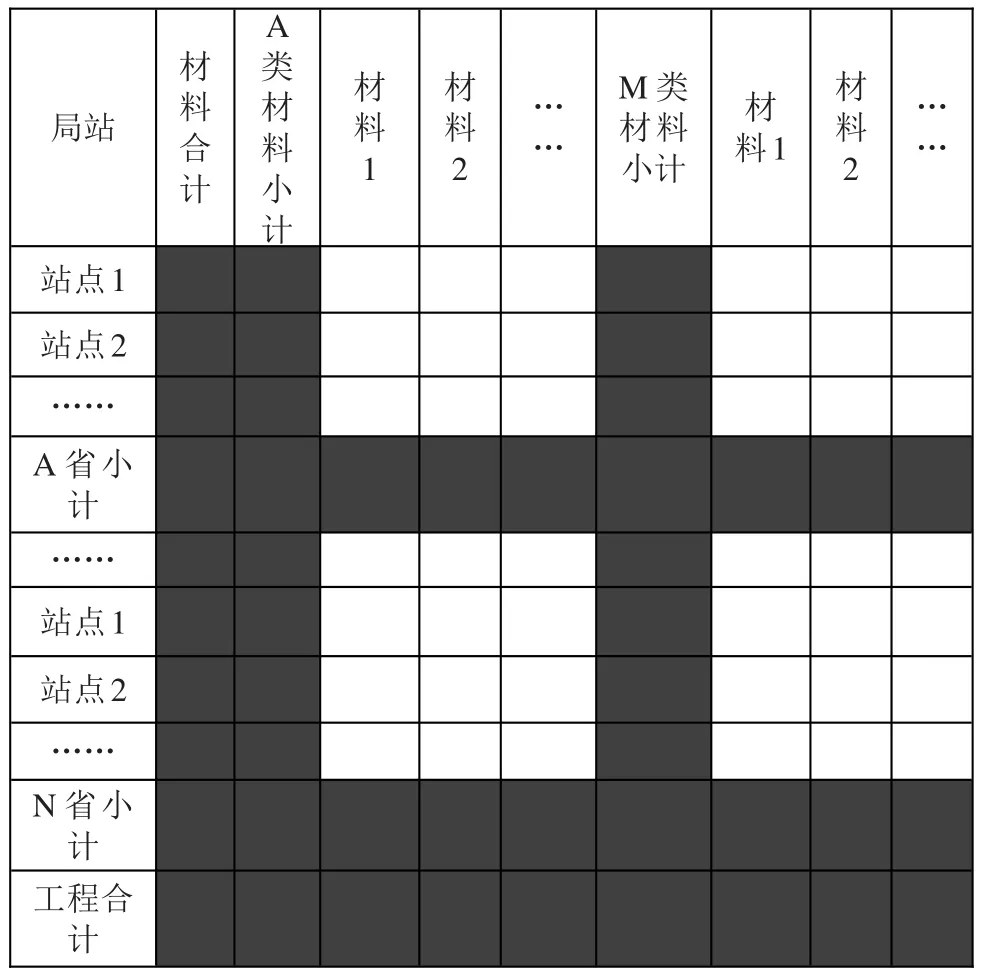
表1 预算汇总表样式
在某些情况下,预算汇总表的金额是不能带小数点的(例如工程预算的批复),因此需要对预算表格进行取整。取整的要求为:所有数据必须为整数,数据取整前后差额的绝对值小于1,数据行列相加等式必须成立。
当材料的类别大于10(M>10)、材料项大于100、站点数量大于100(N>10)时,这将是一个非常庞大的数据表格。除了通信工程设计的预算汇总表外,其他领域也有类似的数据表格需要取整,因此本文研究的内容为大型数据表格的取整算法,以上述表格为例作为研究对象。
2 四舍五入会增加算法复杂度
对小数取整有三种方式:四舍五入、向上取整和向下取整。但是在算法上如果采用四舍五入方式的话,将会增加算法的复杂度,如表2所示。
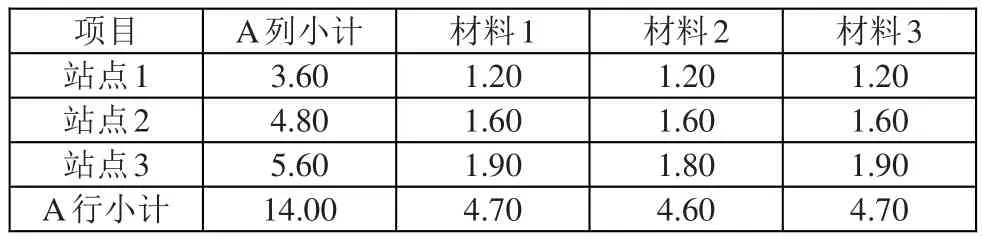
表2 四舍五入取整例子原数据
对表格中的数据四舍五入取整后,需要对部分数据进行加1操作,需要对部分数据进行减1操作,以使得最终的结果满足取整的要求,如表3所示。
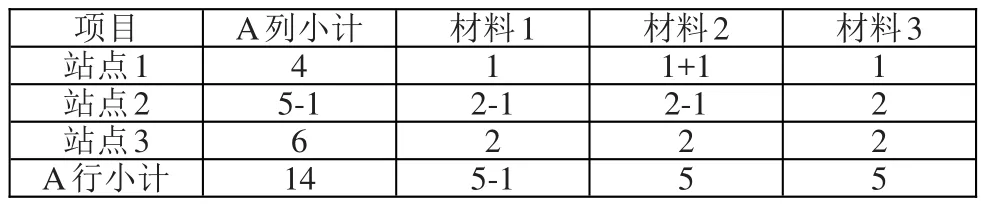
表3 四舍五入取整例子结果
在上述的例子中,数据四舍五入取整后,由于数据小数点后的数值有大有小,导致取整后数据的调整方向有两个,某些数据需要向上加1,某些数据需要向下减1。数据调整方向越多,在算法实现上就会越复杂。如果对数据向上取整或向下取整,取整后数据的调整方向只有一个,向下减1或向上加1,程序实现上较为简单。
为了使算法更为简洁,本文选择向下取整的方式。笔者已经在Excel通过VBA编程实现了取整算法,下面对此算法进行详细的阐述。
3 取整算法
面对庞大且层级较多的数据表格时,为了更方便处理数据,需要对表格进行分析,取得其基本组成单元。通过分析,所有的数据表格均可分为两个基本单元:一维数组和两维数组,下面对这两个基本单元的概念及取整算法说明。
3.1 一维数组表格取整算法
一维数组表格指的是在取整计算时,只需要考虑一个维度(行或列)的等式是否成立即可。具体步骤为:
(1)对数据进行向下取整;
(2)判断和项、细项相加得到的和之间的差额,差额表格需要对细项进行调整的次数或项数;
(3)计算每一个细项取整前后的差额,把差额最大的细项加1。直到第2步计算得的差额为0,即完成了一维数组的取整。
3.2 两维数组表格取整算法
两维数组表格指的是在取整时,需要考虑两个维度(行和列)的等式是否成立,下面以一个两维数组进行详细说明,如表4所示。
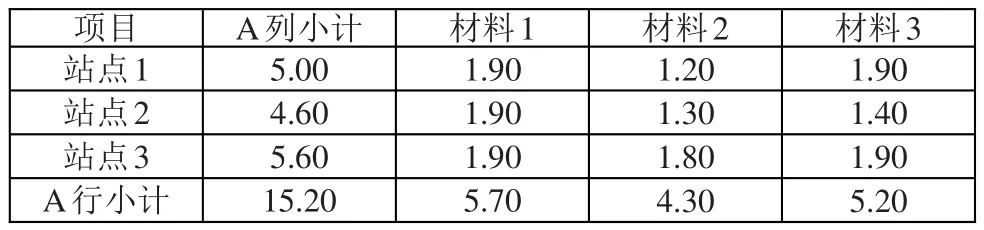
表4 两维数组表格取整算法例子原数据
具体步骤为:
(1)对数据进行向下取整;
(2)判断行、列和项与取整后细项和的差额,求得列差额分别为5-(1+1+1)=2、4-(1+1+1)=1、5-(1+1+1)=2,求得行差额分别为5-(1+1+1)=2、4-(1+1+1)=1、5-(1+1+1)=2,列差额与行差额组成了一个表格的行合计和列合计。使用由上而下、由左而右的方式遍历所有单元格,如其对应的列差额、行差额均大于1,且细项原数据小数点后有数值,即对该单元格进行加1操作,最终得到结果如表5。
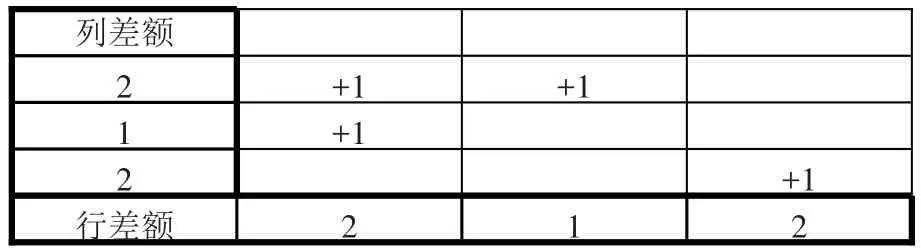
表5 两维数组表格行列差额分配表
(3)完成第2步后,很多时候会存在行列等式不成立的情况,需要对这个表格进一步调整。使用由上而下、由左而右对每一列未加1操作的单元格进行遍历,判断细项原数据小数点后是否有数值,如是即进行加1操作。再判断同一列在第二步已经进行加1操作的单元格,其所在行与不相等列相交的单元格是否已经有加1操作,且细项原数据小数点后有数值的话,加1操作进行互换,如表6所示。
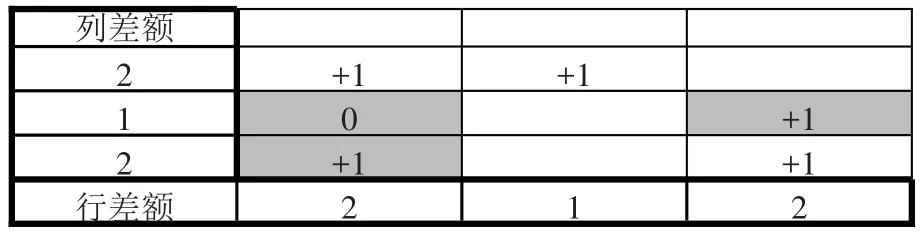
表6 行列差额二次分配表
(4)根据第3步得到的加1操作表格,在数据表格相应位置对向下取整的细项进行加1即完成了两维数组的取整计算。
4 表格分层
对于计算机程序来说,需要将庞大的数据表格进行拆分简化,以方便程序处理。依据该表格的特性,本算法把表格拆分为四个层次的表格。
(1)第一层:提取数据表格的M列小计、列合计与N行小计、行合计相交的单元格,由这些单元格组成第一层表格,如表7所示。
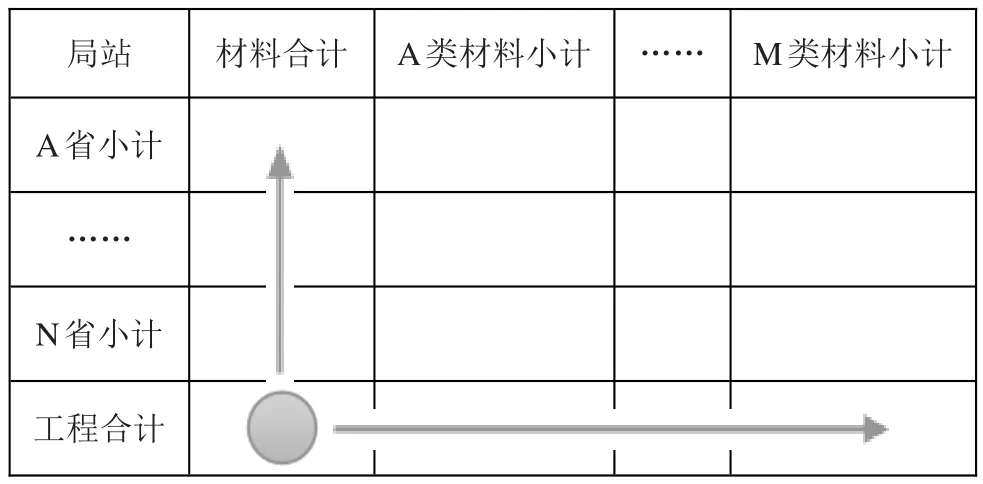
表7 第一层数据表格
首先需要对工程合计数值进行四舍五入,确定数据表格的总和,见上表标圆形的单元格。然后对行合计、列合计进行取整,利用一维数组取整算法处理即可完成。完成此部分后,M列小计与N行小计组成了一个两维数组,利用两维数组取整算法,即可完成第一层数据表格的取整。
(2)第二层:提取数据表格的M列小计、列合计与站点行、行小计相交的单元格,由这些单元格组成第二层表格。第二层共有N个表格,大致表格如表8所示。
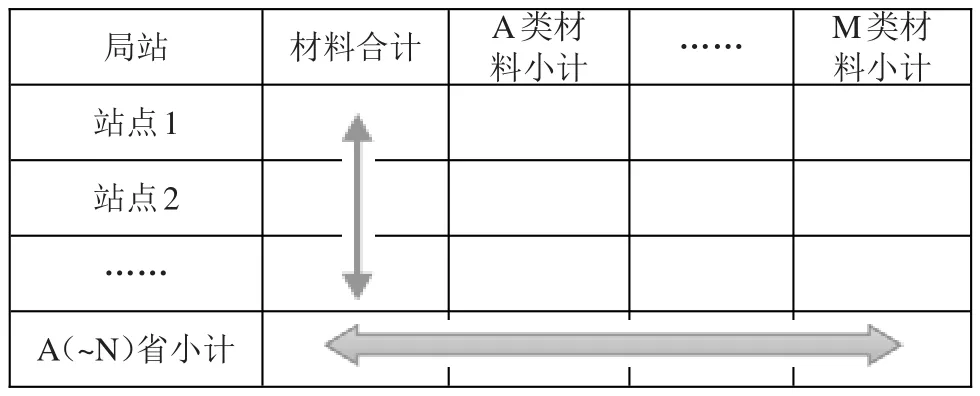
表8 第二层数据表格
通过第一层的调整计算,A(~N)省小计的值已经确定,列合计与站点行相交的单元格组成了一维数组,利用一维数组取整算法处理。完成此步后,M列小计与站点行相交的单元格就组成了一个两维数组,接着利用两维数组取整算法处理。按此步骤把第二层N个表格处理完成后,即完成了第二层的取整。
(3)第三层:提取数据表格的列小计、材料列与行小计、行合计相交的单元格,由这些单元格组成第三层表格。第二层共有M个表格,大致表格如表9所示。
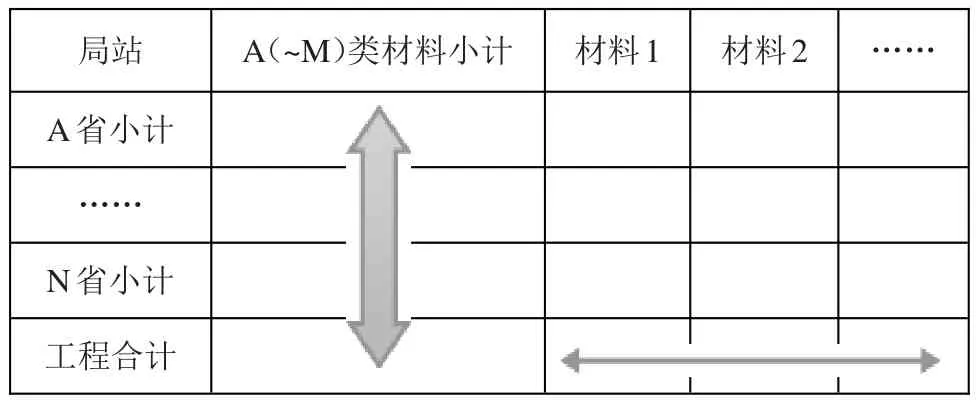
表9 第三层数据表格
通过第一层的取整计算,列小计与行合计相交单元格的值已经确定,通过第二层的取整计算,列小计与行小计相交单元格的值也已经确定。材料列与行小计相交的单元格组成了一维数组,利用一维数组取整算法处理。完成此步后,材料列与行小计相交的单元格就组成了一个两维数组,接着利用两维数组取整算法处理。按此步骤把第三层M个表格处理完成后,即完成了第三层的取整计算。
(4)第四层:提取数据表格的列小计、材料列与行小计、站点行相交的单元格,由这些单元格组成第四层表格。第四层共有M×N个表格,大致表格如表10所示。
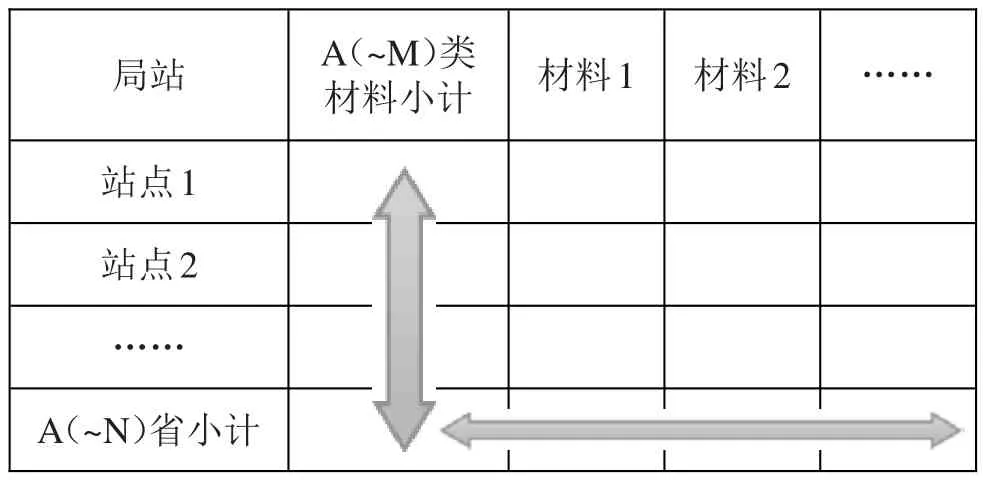
表10 第四层数据表格
通过第二层的取整,列小计与站点行相交单元格的值已经确定,通过第三层的取整,材料列与行小计相交单元格的值也已经确定。材料列与站点行相交的单元格组成了一个两维数组,接着利用两维数组取整算法处理。按此步骤把第四层M×N个表格处理完成后,即完成了第四层的取整计算。
完成以上四个层次表格的取整后,整个大型数据表格的取整工作完成。
5 结束语
本文取整算法的实现,使得大型数据表格的取整工作变得非常简单、快捷,极大地提高了工作效率和节省了人力成本,在实际应用上具有很大的意义。

